对SM4 算法的改进差分故障攻击*
2020-09-12金雨璇杨宏志王相宾袁庆军
金雨璇, 杨宏志, 王相宾, 袁庆军
1. 战略支援部队信息工程大学, 郑州450000
2. 河南省网络密码技术重点实验室, 郑州450000
3. 深圳网安计算机安全检测技术有限公司, 深圳518028
1 引言
为配合我国WAPI (WLAN Authentication and Privacy Infrastructure) 无线局域网标准的推广应用, 2006 年1 月我国自主设计的对称分组密码算法SM4 分组密码算法就此应运而生. 由于该算法加解密速度快、硬件实现简单以及具备一定的安全性, 多适用于制作密码芯片, 现已大量运用于对金融领域、政府部门等的重要数据的保护. 因此单纯通过研究密码算法的数学结构而判断密码算法的安全性已经远远不够, 我们还必须从密码算法的实现角度来考虑更为现实的安全问题. 如果硬件实现上出现了问题, 算法理论安全性再高也无法保证数据的安全性. 如果SM4 算法硬件实现被攻破, 则意味着这些产品不再安全.
针对商用密码算法的硬件实现, 差分故障攻击是一种实际有效的攻击方法, 对密码体制实际安全性造成极大威胁. 随着密码学家们的不断深入研究并改进, 差分故障攻击方法已被运用于对DES[1]、ECC[2]、AES[3]、RC4[4]等众多密码算法的分析中, 并且取得了不俗的成果, 展示了差分故障攻击在密码分析上具有相当强大的可行性. 在不断地应用发展中, 差分故障攻击的实现途径愈加多样、攻击代价逐步降低, 可以非常有效的对密码硬件进行攻击, 成为了对密码体制不容忽视的现实威胁.
如果可以更加快速的完成差分故障攻击, 利用更少的故障注入即恢复出SM4 算法的轮密钥及初始密钥, 或者能够更有效的从可能的密钥中分辨出正确密钥, 就能指导相关芯片的使用者、设计者对加密设备进行保护, 避免这类攻击, 阻止攻击者对其进行故障诱导, 有利于国产密码的研究发展与使用.
本文在前辈工作的基础上做出适当的改进[5],给出SM4 单比特差分故障攻击模型以及具体攻击步骤,理论上只需要一次故障注入, 随后对平均15.3526 比特穷举搜索, 最终可以恢复128 比特的初始密钥. 通过计算机实验对攻击过程进行仿真模拟, 根据实验结果佐证本文中提出的新方案攻击复杂度与理论结果一致, 改进后的攻击方法在一定程度上提高了攻击效率.
本文第2 节详细介绍了SM4 算法的加密流程以及轮密钥扩展方案, 随后整理总结了算法的相关性质与定理; 第3 节具体阐述了差分故障攻击的基本假设以及在该假设下的攻击原理和攻击流程; 第4 节总结了自SM4 算法发布以来, 密码学工作者对其已经进行过的差分故障攻击方法, 并对各方案间的不同进行了对比描述, 指明了各方案的优劣; 第5 节提出对SM4 算法的单比特DFA 方案, 理论推导出攻击复杂度,并通过仿真实验方案及实验结果数据对其加以佐证; 第6 节是对全文工作总结.
2 SM4 算法
2.1 算法简述
SM4 算法由吕述望、李大为、张超等人设计并完成相关标准[6]的起草, 其分组长度和密钥长度均为128 比特, 算法采用非平衡Feistel 结构. SM4 通过32 轮非线性迭代后加上一个反序变换, 方便于解密,解密轮密钥只需要是加密轮密钥的逆序, 而解密算法与加密算法保持一致.
(1) 系统设置
SM4 的加密密钥为MK = (MK0,MK1,MK2,MK3), 其中MKi∈Z322,i = 0,1,2,3. 轮密钥表示为(rk0,rk1,··· ,rk31), 其中rki(i=0,1,··· ,31) 为加密密钥经由密钥扩展方案生成的32 比特第i 轮轮密钥.
FK=(FK0,FK1,FK2,FK3) 为系统参数, CK=(CK0,CK1,··· ,CK31) 为固定参数, 用于密钥扩展算法, 其中FKi(i=0,1,2,3),CKi(i=0,1,··· ,31) 均为32 比特.
设T : Z322→Z322为一个可逆变换, 由非线性变换τ 和线性变换L 复合而成, 即T (·) = L(τ(·)).其中非线性变换τ 由4 个并行的S 盒构成. 设A,B ∈(Z82)4, 非线性变换τ 输入为A=(a0,a1,a2,a3),输出为B =(b0,b1,b2,b3), 即(b0,b1,b2,b3)=τ(A)=(S(a0),S(a1),S(a2),S(a3)).
L 为线性变换, 其输入为非线性变换τ 的输出. 设输入为B ∈Z322, 输出为C ∈Z322, 则C =L(B)=B ⊕(B ≪2)⊕(B ≪10)⊕(B ≪18)⊕(B ≪24). 其中≪表示循环左移.
(2) 加密算法

首先执行32 次迭代运算, 即图1 中所示的轮函数运算, 即计算Xi+4=F (Xi,Xi+1,Xi+2,Xi+3,rki)=Xi⊕T (Xi+1⊕Xi+2⊕Xi+3⊕rki),i=0,1,··· ,31
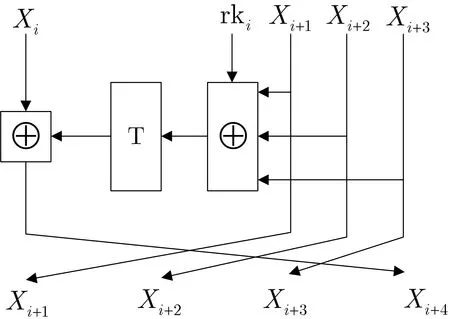
图1 SM4 算法轮函数示意图Figure 1 Schematic diagram of SM4 algorithm round function
然后对最后一轮输出数据进行反序变换得到密文输出,即(Y0,Y1,Y2,Y3)=R(X32,X33,X34,X35)=(X35,X34,X33,X32).
(3) 密钥扩展算法
设加密密钥为MK = (MK0,MK1,MK2,MK3) ∈(Z322)4, 轮密钥生成方法为rki= Ki+4= Ki⊕T′(Ki+1⊕Ki+2⊕Ki+3⊕CKi)(i=0,1,··· ,31), 其中K0= MK0⊕FK0, K1= MK1⊕FK1, K2=MK2⊕FK2, K3= MK3⊕FK3. 系统参数FK 的取值为FK0= (A3B1BAC6), FK1= (56AA3350),FK2=(677D9197), FK3=(B27022DC).
T′变换与T 变换类似, 将T 变换中的线性变换L 替换成L′(B) = B ⊕(B ≪13)⊕(B ≪23) 即可得到.
固定参数CK 取值方法为: 设cki,j为CKi的第j 字节(i=0,1,··· ,31,j =0,1,2,3), 即CKi=(cki,0,cki,1,cki,2,cki,3)∈(Z82)4, 而cki,j=(4i+j)×7(mod256). 其值请参见相关标准文献[6].
(4) 解密算法
解密变换与加密变换类似, 不同的仅是轮密钥的使用顺序, 解密时使用轮密钥序(rk31,rk30,··· ,rk0)即可.
2.2 算法性质
SM4 算法拥有相当优良的抗差分性质, 在文献[7–12] 中分别证明并介绍了此算法多个性质, 以及相关定理推论. 本文主要从S 盒以及线性变换介绍算法的如下5 个性质及3 个定理.
(1) S 盒变换
S 盒的抗差分能力主要从其差分均匀度以及差分分布表两方面刻画, 且具有较小的差分均匀度是S 盒抗差分攻击的必要条件, 以下两条性质说明了SM4 的S 盒具有良好的抗差分性质.
性质1 SM4 的S 盒对于任何非零的输入差分, 存在127 个可能的输出差分. 其中有一个输出差分出现的概率为2−6, 其余输出差分出现的概率为2−7[8].
设a,b ∈Z82, 则利用差分分布表求解给定输入差分a、输出差分b 的差分方程S(x)⊕S(x ⊕a)=b的复杂度由28降至1, 且其解至多有4 个, 也即下述性质2.
性质2 SM4 算法S 盒的差分均匀度仅为4[7].
基于性质1 以及差分分布表, 并给定三元组(x,x∗,y), 对于差分方程S(x ⊕k)⊕S(x∗⊕k) = y, 性质3 描述了其可求解情况的性质.
性质3 以S(·) 表示SM4 的S 盒变换, (x,x∗,y) 为Z82中的随机三元组, 则有下述事实成立:
①差分方程S(x ⊕k)⊕S(x∗⊕k)=y 有解概率为0.4942;
②如果上述方程有解, 则解的个数平均值为2.0236[12].
(2) 线性变换
SM4 算法的线性变换L 由4 个异或操作与5 个移位操作组成(包括移0 位), 以下从SM4 的线性变换表明该算法抗差分性质优良.
分支数概念由J. Daemen 提出, 可以用于评测一个变换, 尤其是线性变换的差分扩散效率, 下面给出其定义:
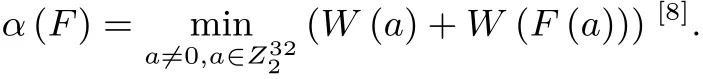
根据定义1 可知, 线性变换F 分支数最大可以达到5. 一般来说, 分支数越大, 线性变换的扩散性质越好. 当F 分支数达到最大时, 我们称F 是最佳扩散的. 而通过实验可证明, 对SM4 的线性变换有以下性质:
性质4 SM4 中线性变换L 的分支数为5[8].

定理1 如果F (X,k,r1,··· ,rk) 是最佳扩散的, 那么必然有k ≥5[9].
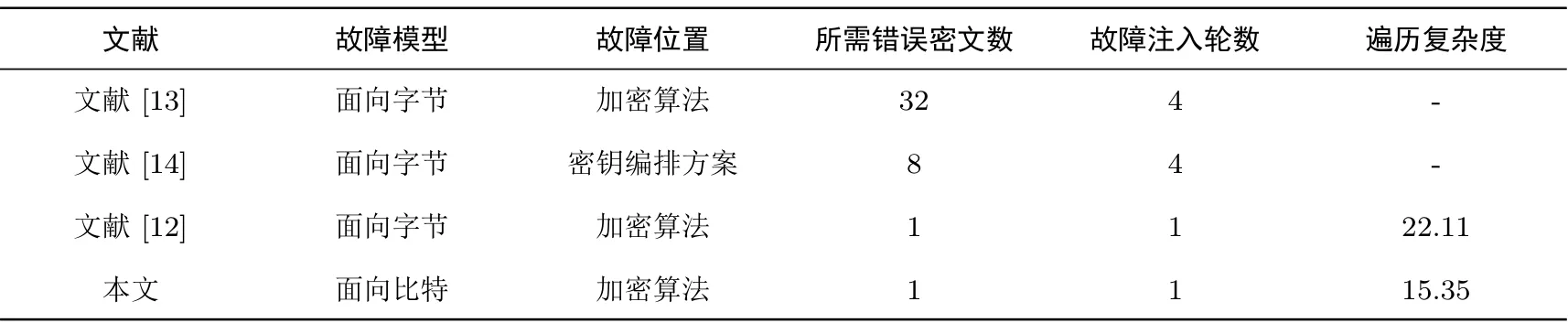
由定理1 可知, SM4 算法若想达到最佳扩散性, 则移位操作必须达到 5 个, 也即 L(B) =F (B,5,r1,··· ,r5). 又由鸽笼原理可知r1到r5中必有两个落入同一字节内. 不失一般性的, 可设r1,r2都落入第一字节, 即0 ≤r1 定理2 在r1,··· ,r5的14 336 种取值中, 只有两种可以使得L 达到最佳扩散性, 分别是SM4 的线性变换L 取值, 以及L 循环左移24 比特, 其本质上是一致的. 综上所述, SM4 算法的线性变换是最佳扩散的,且是移位操作最少情况下唯一的. 最后给出SM4 算法加密算法线性变换的逆变换, 其证明可参看文献[12]: 以分组密码算法为例, 图2 给出了差分故障攻击的原理, 具体可描述如下: 现代分组密码的非线性度大都由S 盒查表操作提供, 而对于某一轮S 盒的未知输入值, 可根据分组密码的结构以及轮函数特性, 通过对密码芯片进行攻击, 导入随机故障值, 使其运行过程的某中间状态产生变化, 导致密码设备给出错误输出. 于是根据得到正确密文与错误密文的差分值, 满足差分方程, 通过差分分析结合轮函数细节求解差分方程, 可以获取该轮输入值以及正确输出值. 再利用运算过程中输入输出值与涉及的相关密钥之间的关系, 得到轮密钥可能值集合, 然后通过多次攻击不断地缩小可能密钥范围, 最终实现轮密钥以及初始密钥的恢复. 为更好地进行差分故障攻击, 通常攻击者遵循的基本假设均为: (1) 攻击者完全掌握密码设备, 可以在加密过程中任意时刻任意位置注入故障, 但故障具体值未知; (2) 攻击者可以获得同一个明文在密钥作用下正确加密得到的密文, 以及诱发故障后产生的错误密文. (3) 攻击者可以多次重启密码设备, 以得到多个不同的错误密文. 在以上的攻击假设下, 差分故障攻击的攻击流程通常由四个步骤构成: 确定故障模型、完成故障注入、进行故障分析、实现密钥恢复. 图3 展示了分组密码算法的差分故障攻击流程. 图2 分组密码算法DFA 原理Figure 2 DFA principle of block cipher algorithm 图3 分组密码算法DFA 流程Figure 3 DFA process of block cipher algorithm 在差分故障攻击方向, 张蕾等人[13]于2006 年首先给出了SM4 算法的差分故障攻击, 该模型采用了面向字节的随机故障模型, 是最基础的DFA 模型. 该模型故障注入位置为各轮的后三个存储器, 理论上完成一轮子密钥的恢复需要8 个错误密文, 仅需要32 个错误密文再结合密钥扩展方案, 就可以完全恢复出SM4 的128 比特种子密钥. 因为实际中故障发生的字节位置是不可能完全平均的, 所以实际攻击所需错误密文数将略大于理论值; 文中的实验结果也验证了这一事实, 恢复SM4 的128 比特种子密钥平均大约需要47 个错误密文. 两年后, 李玮等人[14]对攻击方案进行了改进, 针对密钥扩展方案进行故障注入. 在生成各轮子密钥前注入故障与密钥数据存储器中, 最佳情况下可以影响到该轮的全部S 盒. 最高效率的情况下, 一次故障注入就可以对4 个S 盒都进行有效攻击, 两次注入即可以恢复一轮子密钥, 仅需要8 个错误密文就可以恢复原始密钥. 同时文中给出了判断故障注入处的方法, 便于在攻击过程中对于低效的故障注入直接舍弃,提高了故障诱导的攻击成功率, 减少了错误密文数. 2011 年, Li R L 等人[12]一改之前传统DFA 方案逐轮攻击的方法, 利用SM4 算法独特的差分路径直接对第28 轮进行故障注入, 对后五轮进行统一的攻击. 在攻击者保证发生故障为单字节故障的前提下,这种新式的攻击方法在第28 轮的后三个数据存储器之一诱发故障, 仅需要一次故障注入, 即可恢复初始密钥的大部分信息. 再经过平均次穷举搜索, 最终可恢复SM4 算法的初始密钥. 以上DFA 方案皆是在仿真实验中实现的, 具有较苛刻的理论条件, 2016 年荣雪芳团队[15]提出符合实际攻击状况的方案, 不再要求在固定已知位置注入唯一单字节故障, 而只需要在算法后4 轮随机进行故障注入, 将理论引入了实践. 通过对无防护SM4 算法的智能卡实施该攻击的结果表明, 与其他攻击方法相比, 该方法可扩大故障注入的范围, 提高故障攻击的实用性. 目前针对SM4 算法的DFA 故障注入模型均基于字节注入, 而早在2010 年, Agoyan 等人就已经利用激光的手段实现了对微控制器的单比特故障注入[16]. 更高精度的故障注入可以对算法硬件实现进行更高效的攻击, 因此现有故障模型无法准确分析评估算法差分故障安全性. 并且, 由于单比特故障注入模型的故障值集合较小, 理论上针对各算法的差分故障攻击均能有不同程度的效率提高. 针对激光注入等高精度故障注入技术, 本文在文献[12] 的基础上进行改进, 提出了一种针对SM4 算法的单比特的差分故障攻击模型. 本模型基于以下的基础假设: (1) 攻击者可以获得同一密钥作用下的正误密文对, 且密钥未知. (2) 攻击者可以诱发单比特的随机故障. 本文采用的攻击模型为单比特的随机故障模型, 攻击的基本过程为 (1) 选择明文攻击, 获取明文在密钥作用下的正确密文; (2) 重新加密明文, 加密进行至第28 轮时, 在第四个存储器中注入故障, 随后完成后续加密得到错误密文; (3) 通过差分分析推测最后一轮轮密钥可能值; (4) 在得到最后一轮轮密钥可能值集合的基础上, 推测得到倒数后四轮轮密钥可能值集合; (5) 利用第四步得到的所有轮密钥逆推得到初始密钥可能值集合; (6) 通过暴力攻击, 从初始密钥可能值中得到正确密钥. (1) 计算∆Bj=L−1(∆Cj); (2) 以ai表示∆Aj的第i 个字节(i=0,1,2,3), 记为ai=(∆Aj)i, 也即∆Aj=a0||a1||a2||a3, 同理bi=(∆Bj)i; (3) 根据ai,bi, 结合性质1给出的差分分布表可以得到各字节所有可能输入值INj(ai,bi). (4) 推导密钥与输入输出间的关系(rkj−1)i= (Aj)i⊕INj(ai,bi), 可以得到密钥rkj−1的第i 个字节可能值集合ki; 根据上述攻击过程以及性质3, 给定二元组(∆A,∆C), 可以得到如下结论: 本节对具体的攻击过程进行详述. (1) 获取正误密文对 随机选择一个明文X = (X0,X1,X2,X3), 并对其正确加密获得正确密文Y = (Y0,Y1,Y2,Y3). 在同样的密钥作用下对明文再次加密, 在加密过程中对第28 轮注入1 比特的故障 (2) 猜测后四轮密钥值 由于明文以及正误密文对已知, 而加密算法的最后进行的逆序变换易于求逆, 因此可利用上文提到的基本攻击方法对后四轮逐轮进行差分攻击, 分别推导出第32 轮到第29 轮的轮密钥. 计算A32=X32⊕X33⊕X34⊕rk31,A∗32=X∗32⊕X∗33⊕X∗34⊕rk31, 则对于第32 轮T 变换, 其输入差分和输出差分分别为 此时利用前述基本攻击方法可得rk31可能值集合rk31 利用①步中得到的所有轮密钥可能值, 对正误密文进行一轮的解密可以得到 对得到的所有二元组(∆A31,∆C31) 进行基本攻击, 得到可能密钥集合rk31,rk30. 用②步中得到的所有(rk31,rk30)∈rk31,rk30, 对正误密文进行两轮的解密可以得到 考虑第30 轮的轮函数, 计算所有可能的 利用其对第30 轮进行基本攻击, 由每组(∆A30,∆C30) 求得后三轮密钥候选值集合rk31,rk30,rk29. 与上节同理, 首先用③步中得到的所有(rk31,rk30,rk29) ∈rk31,rk30,rk29, 对正误密文进行三轮的解密可以得到 考虑第29 轮的轮函数, 计算∆A29,∆C29所有候选值, 其中 对第29 轮进行基本攻击, 由每组(∆A29,∆C29) 求得后四轮密钥候选值集合rk31,rk30,rk29,rk28. (3) 恢复初始密钥 利用密钥扩展方案的逆, 对步骤2 中得到的所有密钥可能值求逆, 得到初始密钥候选值集合MK.用MK中所有初始密钥候选值对正确密文解密, 并判断是否与明文相同. 由于密钥固定时, 密码算法都是明文集合到密文集合的双射, 所以最终仅可能有一个密钥通过判断. 根据上一节提出的攻击方法可知, 最终恢复出的密钥个数不止一个. 因此本节从理论上给出各轮轮密钥可能值个数的期望, 用以描述攻击复杂度. (1) rk31个数期望值 在完成第32 轮的基本攻击时, 由差分路径以及轮函数运算规则可以得到∆X31= L(∆B28), 那么可 得 若记L−1(∆X35)∆=(d0,d1,d2,d3), 则可知∆B32有四类可能取值 其中0 ̸= γ ∈F82为∆B28中故障发生字节的对应值. 对于单比特故障的情况, γ 可能值经实验知有254个, γ 不会取值0x7F. 记∆A32∆= (a0,a1,a2,a3), 对照差分分布表, 对所有i = 0,1,2,3 比对是否存在输入差分为ai, 输出差分为di. 若存在某0 ≤i ≤3, 使得S(x)⊕S(x ⊕ai) = di无解, 则说明该字节为故障发生字节. 不失一般性的, 可以假设i = 3 时方程无解. 若为此情况, 前三字节密钥可以通过差分分布表得到可能取值,第四字节密钥则需要遍历得知. 在这种情况下, 得到的第32 轮轮密钥的可能值集合rk31中, 平均有(2.0236)3×254×0.4942×2.0236 ≈211.0395个元素. 若不存在, 也即对∀i,0 ≤i ≤3,S(x)⊕S(x ⊕ai)=di都有解, 此时无法判断故障发生的字节. 由于注入的故障可能发生在任一字节, 故∆B28可能有1016 个可能值. 此时得到的第32 轮轮密钥的可能值集合中平均有(2.0236)3×1016×0.4942×2.0236=213.0395个元素. 由于∀i,0 ≤i ≤3,S(x)⊕S(x ⊕ai) = di有解的可能性为0.4942, 故第32 轮子密钥可能值集合的元素个数平均为(1 −0.4942)×211.0395+0.4942×213.0395≈212.3514. (2) (rk31,rk30) 个数期望值 如果在上一步已知故障发生字节, 则∆X30= E 有8 种可能取值, 而∆X34是固定已知的, 因此相应的可知∆C31= ∆X30⊕∆X34= E ⊕∆X34有8 种取值. 此时可以推知RK31,RK30中元素个数期望值约为211.0395×8×2−4.0673×24.0677= 214.0399; 否则∆X30有32 种可能取值, 进而可知cardRK31,RK30=213.0395×32×2−4.0673×24.0677=214.0399=216.0399. (3) (rk31,rk30,rk29) 个数期望值 在本轮攻击中, 由于∆C30= ∆X33是确定的值, 可由密文直接得到, 因此rk29求取情况取决于得到的本轮差分方程组的个数, 以及其是否可解. (4) (rk31,rk30,rk29,rk28) 个数期望值 与上节同理, ∆C29=∆X32可由密文直接得到. 此时如果已知故障发生位置, 则可知 为验证本文中攻击方法的攻击复杂度理论值的正确性, 在普通PC 机器(CPU 为Intel(R)Core(TM)i5-6200U @ 2.30 GHz 2.40 GHz, 内存8 GB) 上使用C 语言(Visual C++ 6.0) 编程实现本文提出的攻击方法的仿真实验. 每次实验的明文以及密钥数据皆由计算机随机生成, 不含任何特殊要求, 利用计算机模拟故障注入过程, 得到正误密文. 编号 rk31 (rk31,rk30) (rk31,rk30,rk29) (rk31,rk30,rk29,rk28) 故障位置 遍历复杂度(bit)1 2064 18 432 26 624 65 024 第2 字节 15.9887 2 2032 18 432 20 480 65 152 第4 字节 15.9915 3 8128 257 536 221 184 130 048 未知 16.9887 4 8128 243 456 276 480 203 264 未知 17.6330 5 8136 242 688 243 712 204 800 未知 17.6439 6 2064 17 792 40 960 65 152 第3 字节 15.9915 7 8128 263 680 245 760 199 168 未知 17.6036 8 2048 16 896 28 672 65 152 第1 字节 15.9915 9 2048 16 128 8192 65 024 第2 字节 15.9887 10 8128 263 936 278 528 132 480 未知 17.0154 我们进行了1000 次实验, 本文给出前十次的实验数据如表1所示, 其中2 到4 列表示对应项元素个数. 由表中数据可以看出, 每次攻击经过较低复杂度的暴力攻击即可以成功恢复128 比特的SM4 初始密钥. 当可推知故障发生位置时, 最终的遍历复杂度约为216; 未知故障发生位置时, 遍历复杂度稍高, 约为217.5. 另外, 实验数据略高于理论推导值, 这是由于在推算暴力攻击的理论值时, 认为SM4 算法的差分方程解平均为2.0236 个, 但是实际上据差分分布表可知存在差分方程的解为4 个. 对每一轮的攻击需要对4个字节的差分方程进行求解, 只要有一个方程的解为4 个, 最终暴力攻击的复杂度就会增大1 比特. 一次完整的攻击需要求解16 个方程, 是完全有可能出现4 解方程的, 因此在实验中认为偏差2 比特都是可以接受的. 图4 展示了1000 个实验数据的统计图, 由此可看出, 总体上实验数据是符合理论推导值的. 本文在总结对比已有的针对SM4 算法的差分故障攻击的基础上, 面对现有故障注入能力大幅度提升的现状, 本文给出了一个针对SM4 算法的改进的差分故障攻击方案. 通过理论推导可知, 本文提出的攻击模型仅需要通过在第28 轮的第4 个数据存储器中诱发一次单比特故障, 再经过对平均15.3526 比特的穷举搜索, 最终可以恢复128 比特的初始密钥. 并且, 通过计算机实验仿真模拟可以佐证本文中提出的新方案攻击复杂度与理论结果一致. 在表2 中, 展示了本文与针对SM4 算法的已有差分故障攻击的结果对比.结果显示, 本文提出的新攻击方案较以往的方案相比攻击效率有较为明显的提升. 下一步的研究方向是考虑多次单比特故障注入的情况, 进一步提高攻击效率优化攻击性能. 另外, 基于单比特故障攻击模型的假设较强, 下一步工作可以通过调整攻击相关参数, 在模型假设条件与攻击效率之间寻找平衡. 在未来的研究中, 将扩展本文提出的攻击模型的分析对象, 继续研究针对其他算法的单比特差分故障攻击. 文献 故障模型 故障位置 所需错误密文数 故障注入轮数 遍历复杂度文献[13] 面向字节 加密算法 32 4 -文献[14] 面向字节 密钥编排方案 8 4 -文献[12] 面向字节 加密算法 1 1 22.11本文 面向比特 加密算法 1 1 15.35
3 差分故障攻击
3.1 DFA 原理
3.2 基本假设及攻击流程


4 SM4 算法DFA 研究进展
5 改进的SM4 算法差分故障攻击
5.1 故障模型
5.2 基本过程
6 SM4 算法的单比特DFA 攻击
6.1 基本攻击方法


6.2 攻击过程详述

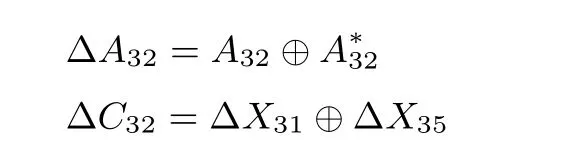



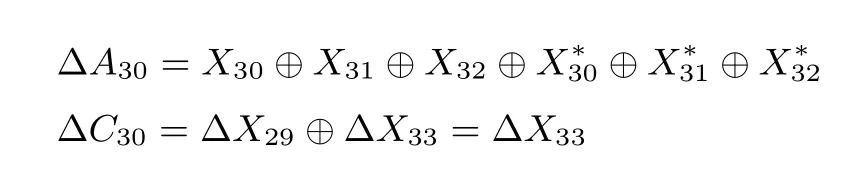
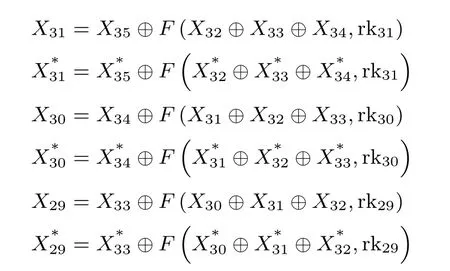
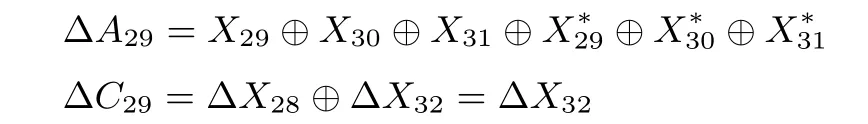
6.3 攻击复杂度分析
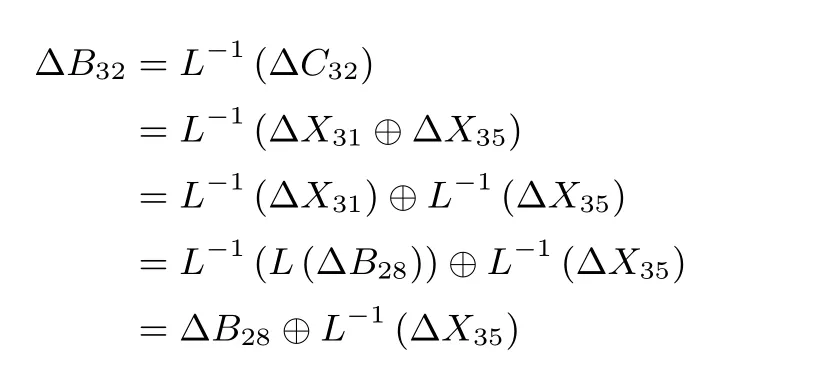

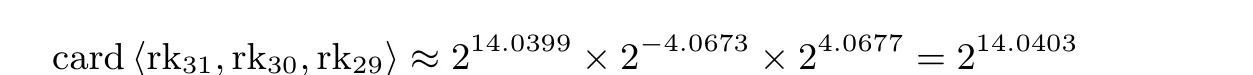


7 攻击实验结果

8 总结与展望