插值Loop曲面细分算法在堆焊自由曲面重建中的应用

洪波 李鹏 吴宏宝 陈实

(湘潭大学 机械工程学院∥焊接机器人与应用技术湖南省重点实验室，湖南 湘潭 411105)

自由曲面重建技术是逆向工程中的关键步骤，其主要思想是通过扫描物体获取物体表面的三维信息，预处理采样点云也即待重建物体表面的三维信息，构造采样点云之间的拓扑关系并利用计算机技术逐步还原物体的本来形貌。

在一些特定场景，产品的已有技术信息丢失，就需要反向得到产品的三维信息。逆向工程可以做到产品的再复原，主要方法是曲面重建，主要任务是采集点云数据，对数据进行预处理，然后选择合适的重建方法对数据进行网格划分，利用计算机还原物体的原有形貌。在焊缝信息检测中，电弧传感器和激光传感器的应用较为广泛。激光传感器由于其非接触、信息量大等优点而得到了广泛的应用，但基于视觉传感的图像处理复杂，降低了实时性，而且待测试样表面形态对数据采集的影响较大。旋转电弧传感器具有实时性强、可达性好、抗弧光等特点,已被越来越多地用于焊缝跟踪。

在堆焊的相关研究过程中，苏伯中[1]针对法兰密封槽曲面人工堆焊耗时费力、精度较低的情况，基于PLC控制伺服系统和步进系统多轴联动实现法兰密封槽曲面的自动堆焊，该方法定位准确、精度较高；兰强等[2]针对自由曲面自动堆焊不等厚问题，设计了驱动电路及数字电子电位器，该方法的自由曲面自动堆焊效率高，可实现自由曲面自动堆焊等厚焊接；温强[3]针对自由曲面表面修复难的问题，在dsPIC30f6011的基础之上设计了一套自动堆焊系统，该系统结构简单、运行稳定；洪波等[4]针对多层堆焊表面变形较大、堆焊困难的问题，提出了分区间Kriging插值增长的Delaunay模型，就堆焊实验效果来看，实现了堆焊表面曲面重建，但应用范围与跟踪精度不是特别理想。

本文针对堆焊自由曲面焊缝形貌不规则致使焊缝识别精度低、自动焊接困难的问题，利用旋转电弧传感器，提出了一种利用插值Loop曲面细分算法对旋转电弧传感器采集的堆焊焊缝三维形貌数据进行曲面重建的方法。首先采用格拉布斯(Grubbs)检验算法[5]对异常采样点进行过滤处理，然后采用局部最优Delaunay算法对采样点的三维数据进行初始三角网格剖分，最后利用插值Loop曲面细分算法对初始三角网格进行曲面细分处理，实现焊缝三维形貌重建。

1 自由曲面采样点坐标分析

为了确定电弧采样点的空间坐标，以电弧旋转中心为坐标原点o，焊接方向为X轴，焊枪轴线为Z轴，建立空间直角坐标系,如图1所示。其中，电弧旋转半径为r，角速度为ω，X(t)=rcos(ωt)，Y(t)=rsin(ωt)，电弧长度用H(t)表示，将其离散化为H(i)，X(i)，Y(i)。

图1 旋转电弧的空间位置图Fig.1 Space position map of rotational arc

将旋转一周的电弧视作一个空间平面[6]，任何角度的电弧平面均可表示为

Z=AX+BY+C

(1)

变形为

Z=β0+β1X1+β2X2

(2)

令β=(β0,β1,β2)T,

(3)

式中，n为拟合次数。

式(3)可变形为

(4)

即

β=(XTX)-1XTH

(5)

将β代入式(2)中，即可求得Z值，式中的H则由传感器采集得到的电流值转换后得到。

2 数据预处理

为了保证对采样点的实时处理而不影响焊接进程，本文以8个连续旋转周期为采样周期，并且每个旋转周期只取前半周期的采样点进行处理，即每周期取32个采样点，以期达到最佳的焊缝形貌重建效果。影响形貌质量最为直接的参数是其采样点的高度数据即Z值，因此本文根据Z值，采用Grubbs检验算法[5]对采样点进行过滤。

为了检验Z(i)(i=1,2,…,n)中是否存在可疑数据，先根据Z(i)数值大小对其进行升序排列，得到Z(1)≤Z(2)≤…≤Z(n)。

在指定的显著性水平β(通常β=0.05)下，求出判别可疑值的临界值g0(β,n)，格拉布斯检验算法的判别公式为

g≥g0(β,n)

(6)

如果满足式(6)，则认为可疑值Z(i)是异常的，应予舍去。以第一个前半周期采样点数据为例，经过上述算法处理后，结果如图2所示，剔除了异常采样点，可得到质量较高的数据,以便后续使用。

图2 异常采样点数据过滤处理前后的比较

3 焊缝三维形貌的重建

3.1 三维数据的初始三角网格剖分

首先采用局部最优Delaunay三角剖分算法对采样点集进行切平面的网格划分，然后利用经计算得到的网格顶点的法向量，基于二维平面的网格计算，可得到三维空间的Delaunay 三角网格[7]。

3.1.1 局部最优Delaunay 三角网格剖分

图3 最小内角最大化准则Fig.3 Maximization criterion of inimum internal angle

根据上述判别准则，局部最优Delaunay 三角网格剖分的基本计算步骤如下：

(1)增加3个辅助点以构造能够包含所有进行三角剖分的点的初始三角网格；

(2)寻找包含点集P中未处理过的点x的三角网格，并将x与该三角网格的3个顶点相连，在产生新的三角网格的同时删除原三角网格，按照上述准则对平面所有网格进行角度调整，使该平面网格达到最优化；

(3)删除增加的点及与之相连的三角网格，由此形成了局部最优的Delaunay 三角网格。

3.1.2 网格顶点的法向量计算

给定网格顶点V的最近点集Q={Qi|i=1，2，…，k}⊂P，若V点满足

(7)

则C的最小特征值对应的特征向量即为最优法向量N[9]，将N代入3.1.1节中得到的二维三角网格，即可形成三维三角网格T。

3.2 插值Loop曲面细分

曲面细分主要经反复细化初始三角网格进而多次生成控制网格顶点实现，求出控制网格M,使用M的顶点对点集P进行插值,即M中顶点的细分极限位置与T中顶点重合[10]。

(8)

以三角网格T的顶点vi为初始值，采用Richar-dson松弛迭代法求解M中的顶点xi，其迭代公式及相应的盈亏公式如下：

(9)

式中，μ取经验值0.14，此时的收敛速度较快，pij的计算公式为

(10)

(11)

(12)

盈亏修正公式如下：

(13)

(14)

基于上述迭代算法，插值Loop曲面细分三维数据的主要处理步骤如下：

(1)输入三维数据P,经局部最优Delaunay三角网格剖分算法处理，得到三角网格T。

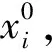
采用局部最优Delaunay算法对预处理后的采样点进行初始三角网格剖分，结果如图4(a)所示，网格稀疏，曲面不够光滑[12]。然后采用曲面细分算法进行处理，结果如图4(b)、4(c)所示，经过两次细分后，网格足够密集，焊缝表面光滑，细分之后的焊缝坡口形貌更规则、更合理。焊缝坡口形貌重建效果良好，明显降低了Delaunay算法处理后的误差，整体算法流程共用时68.35 ms，表明计算时间短，算法重构精度高[13]。

图4 曲面细分效果Fig.4 Curved surface subdivision effect

提取两次细分之后的网格中与初始采样点横、纵坐标相同的坐标点，将坐标Z与初始采样点坐标Z做差处理，进而拟合成三维曲面，可得到误差云图，如图5所示。从图中可知,高度越高，颜色越深，误差越大，图中凸起处即为焊缝处，表明误差主要集中在焊缝坡口处，符合实际情况，细分网格的误差在0.15～0.60 mm之间，满足精度要求[14]。

图5 三维曲面的误差云图Fig.5 Deviation contours of 3D surface

4 焊缝跟踪实验及结果分析

经过上述局部最优Delaunay算法处理后，即可得到空间的三维细分网格，实现堆焊自由曲面的焊缝重建，并利用串口通信将形貌信息传递至自动焊接系统的信息处理模块，经其处理后又将焊缝角度和偏差等信息反馈至执行机构，执行机构据此实时调节焊枪位置与角度，实现自动焊接。自动焊接系统的整体执行流程如图6所示[15]。

图6 自动焊接系统流程图Fig.6 Flowchart of automatic welding system

根据插值Loop曲面细分算法的原理，本文进行了旋转电弧的堆焊自由曲面焊缝重建及焊接实验，实验参数如下：焊件尺寸为250 mm×100 mm×8 mm；电弧电压为12 V，初始焊接电流为200 A，焊接速度为4.5 mm/s，初始焊炬高度为14 mm，电弧采样频率为25 Hz，电弧旋转半径为6 mm，CO2流量为20 L/min。

堆焊实验效果如图7所示，从图中可知，本文方法根据堆焊层焊道坡口的曲面重建模型识别焊道排布偏差变化小，适用范围较广，且偏差识别精度高，焊道自动排布效果较好，堆焊焊缝成型质量也较好[16]。

图7 堆焊实验结果分析Fig.7 Results analysis of build-up welding experiment

5 结论

本文提出了一种基于插值Loop曲面细分算法的旋转电弧堆焊自由曲面焊缝重建的方法，采用局部最优Delaunay算法对形貌数据进行处理，得到初始三角网格，再通过对初始三角网格进行多次细分来实现焊缝形貌还原。实验结果表明：该算法有效避免了传统曲面拟合算法复杂、计算量大、实时性差的缺点，计算精度满足旋转电弧对堆焊自由曲面识别的要求，实现了堆焊的跟踪；该算法降低了初始三角网格的误差，曲面重建效果良好，实用性强。