考虑局部磨损和空化效应的径向滑动轴承混合润滑分析

宋新涛 孙士青 吴维

(北京理工大学 机械与车辆学院，北京 100081)

径向滑动轴承是转子系统的重要部件，其润滑性能直接影响到整个系统的可靠性。在启停、过载的工况下，轴承和轴颈发生接触，导致磨损发生。磨损会破坏轴瓦表面，改变间隙，最终使润滑偏离设计。因此，有必要对轴承磨损后的润滑性能进行分析和预测。

围绕着磨损后轴承润滑性能的研究已经取得了一系列进展。Dufrane等[1]基于对汽轮机轴承磨损的测量结果，建立了两个几何模型用于表征磨损的轴瓦的形状。第一个模型是基于压印概念，即磨损后的弧度半径等于轴颈半径；第二个模型是基于磨粒磨损模型，磨损后的弧度半径大于轴颈半径，后者更接近实际情况。Sharma等[2]分析了不同宽径比对磨损后轴承润滑性能的影响，发现小宽径比轴承的静态性能受磨损的影响较大。在复合材料方面，陆龙生等[3]研究了碳纤维复合材料的摩擦磨损特性。Liu等[4]分析了局部磨损对水润滑橡胶轴承润滑特性的影响，分别分析了在相同偏心率和相同外力下不同磨损深度对轴承润滑性能的影响。然而，现有的关于磨损后轴承润滑性能的研究均是集中在流体动压润滑状态下，且没有考虑空化效应的影响。为了提高机械效率，目前普遍使用低黏度润滑介质[5]，轴承和轴颈不可避免地发生接触。对于滑动轴承润滑性能分析，边界条件的选择是求解的关键。目前常用的是雷诺边界条件和质量守恒边界条件(Jakobsson-Floberg-Olsson，JFO)[6- 7]。雷诺边界条件应用在油膜破裂处较合理，但无法解释油膜再形成时的情况。JFO边界条件将整个润滑区分为油膜完整区和空化区。Elrod[8]提出的算法可以将描述油膜完整区和空化区的方程统一成一个通用方程。Payvar等[9]对文献[8]算法进行了改进，提高了其数值稳定性和收敛性。因此，为分析磨损的轴承润滑性能，应该采用JFO空化边界条件。

本文同时考虑局部磨损和空化效应的双重影响，建立了滑动轴承混合润滑模型，并利用有限差分法对混合润滑模型进行求解，然后通过大量的数值模拟分析不同磨损深度对轴承混合润滑性能的影响。

1 数学模型

1.1 考虑磨损的膜厚方程

基于Dufrane等[1]提出的模型，轴承磨损后的几何形状如图1(a)和图1(c)所示，其中Ob、Oj分别为轴承和轴颈的轴心。油膜的厚度是轴承磨损前的膜厚与磨损区域的叠加，膜厚方程为

h=c[1+εcos(θ-ψ)]+δ

(1)

式中，c为半径间隙，ε为偏心率，θ为周向展开角，ψ为偏位角，δ为磨损深度，

(2)

θs为磨损区域起始角，θf为磨损区域终止角，δ0为最大磨损深度。

确定起始角的方程为

0=δ0-c(1+cosθ)

(3)

在稳态情况下，轴承中心的静态平衡位置可由流体承载力Foil、微凸体接触承载力Fasp和外载荷W的平衡方程获得，如图1(b)所示。载荷平衡方程为

W+Foil+Fasp=0

(4)

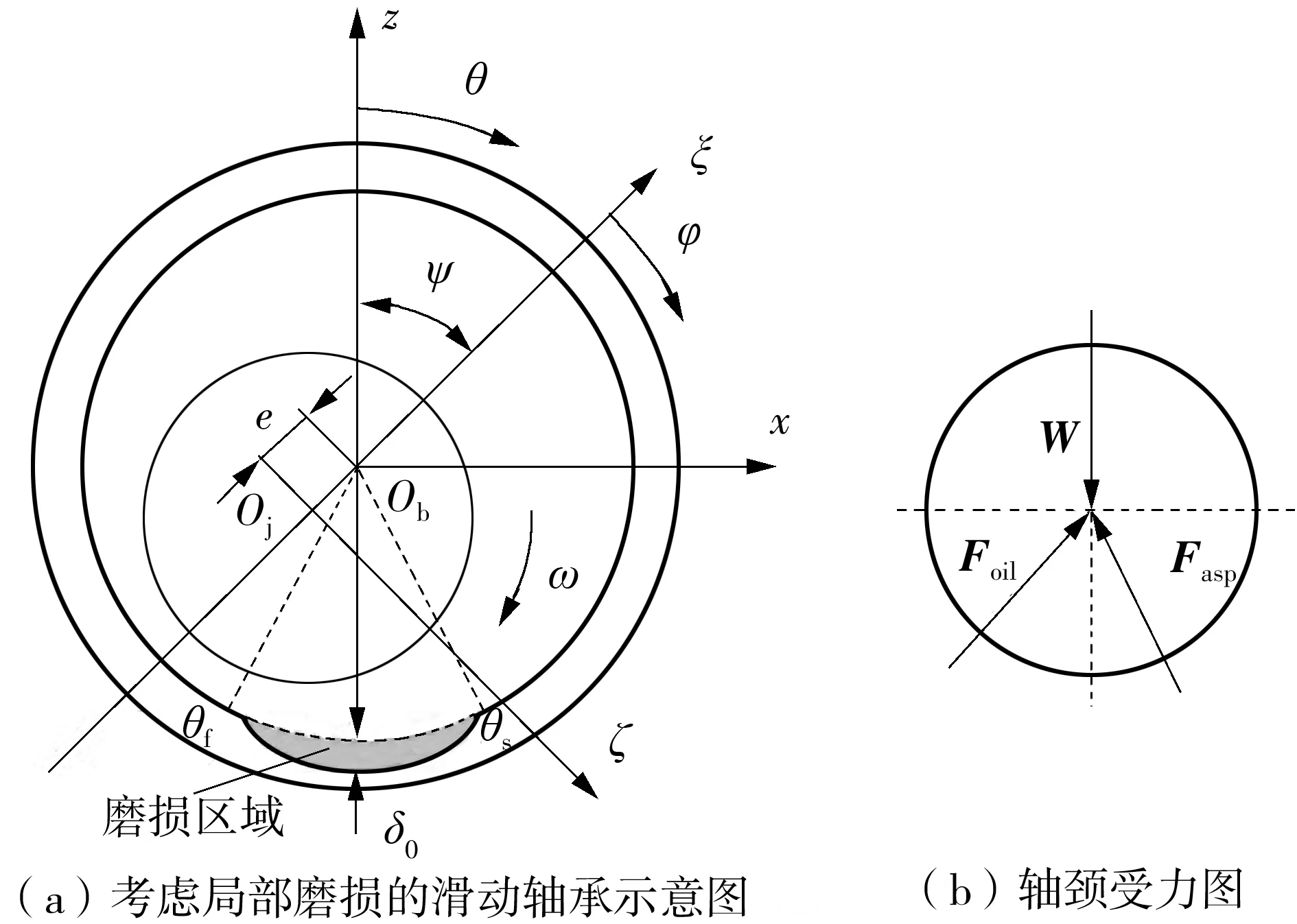
图1 磨损后轴承的几何模型与轴径受力分析Fig.1 Geometry model of worn bearing and journal force analysis

1.2 考虑空化效应的混合润滑模型

平均雷诺方程由Patir和Cheng[11]提出。考虑JFO空化效应的平均雷诺方程为

(5)

式中：φx、φy和φs为流量因子[11]；φc为粗糙峰接触因子[12]；η为润滑油黏度；σ为综合表面粗糙度；h为名义膜厚；pc、pref分别为空化压力和参考压力；F为空化指数，F=(p-pc)/(pref-pc)；φ为独立变量;ρ/ρc=1+(1-F)φ，ρ为空化区润滑油的密度，ρc为全膜区润滑油的密度，是恒定值；U为轴颈速度。

平均流体动压力为

(6)

通过对方程(6)积分，可以获得流体承载力Foil，流体承载力在水平方向的分力Foilx和在竖直方向的分力Foilz分别为

(7)

(8)

式中，A为轴承展开后的面积。

1.3 微凸体接触力

当轴承处于混合润滑时，微凸体与润滑油共同承担外载荷。根据Greenwood和Tripp[13]提出的粗糙峰接触模型，微凸体接触力为

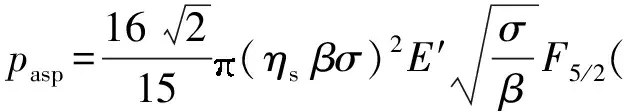
(9)

(10)

微凸体接触压力在水平方向和竖直方向的分力分别为

(11)

(12)

1.4 摩擦系数

根据文献[15]，混合润滑状态下流体的平均剪应力为

(13)

式中，φf、φfs、φfp为剪应力因子[15]。

流体剪切摩擦力为

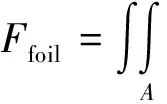
(14)

微凸体接触摩擦力为

(15)

式中，fasp为边界摩擦系数。

总摩擦力为

Ff=Ffoil+Ffasp

(16)

摩擦系数为

f=Ff/W

(17)

2 数值计算方法及验证

2.1 计算方案

为了考虑局部磨损和空化效应对轴承混合润滑性能的影响，本文建立如图2所示数值计算流程图。

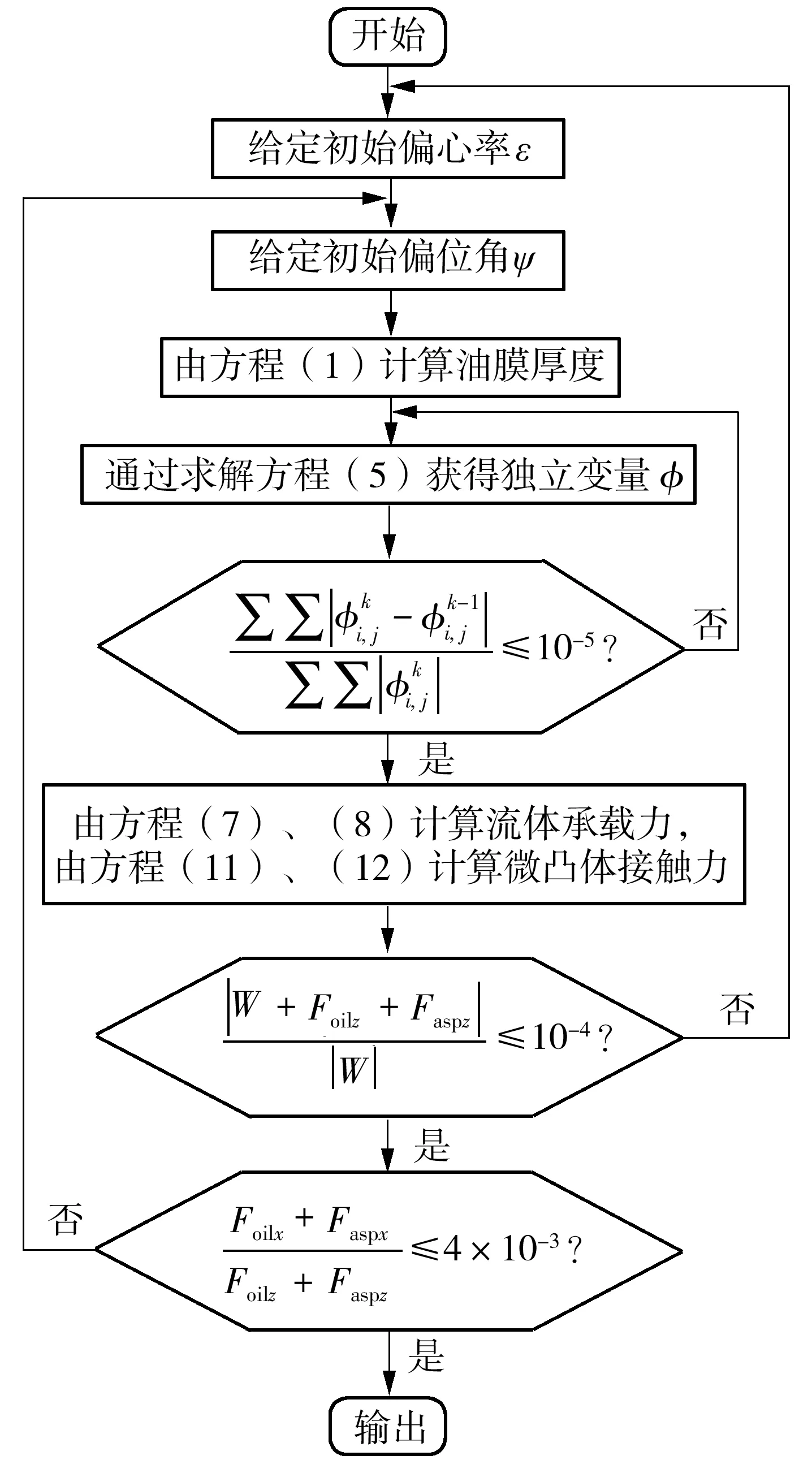
图2 数值计算流程图Fig.2 Flowchart of numerical calculation

在数值计算过程中，有3层收敛准判断，从上到下依次为独立变量的收敛判断、合力与外力大小的收敛判断、合力与外力方向的收敛判断。此处合力指的是流体与微凸体承载力的合力。

2.2 程序验证

为了验证程序的正确性，将本文计算结果与文献[6]的实验结果进行了比较，结果如图3所示。从图中可知，本文计算结果和文献[6]实验测得的油膜压力吻合较好。需要注意的是，上述验证不包含混合润滑状态，为了进一步验证混合润滑模型的正确性，将本文模型计算的Stribeck曲线与文献[16]的Stribeck曲线进行了比较，数据基本吻合，如图4所示，其中的微小差别可能跟网格数与收敛精度的选取有关。

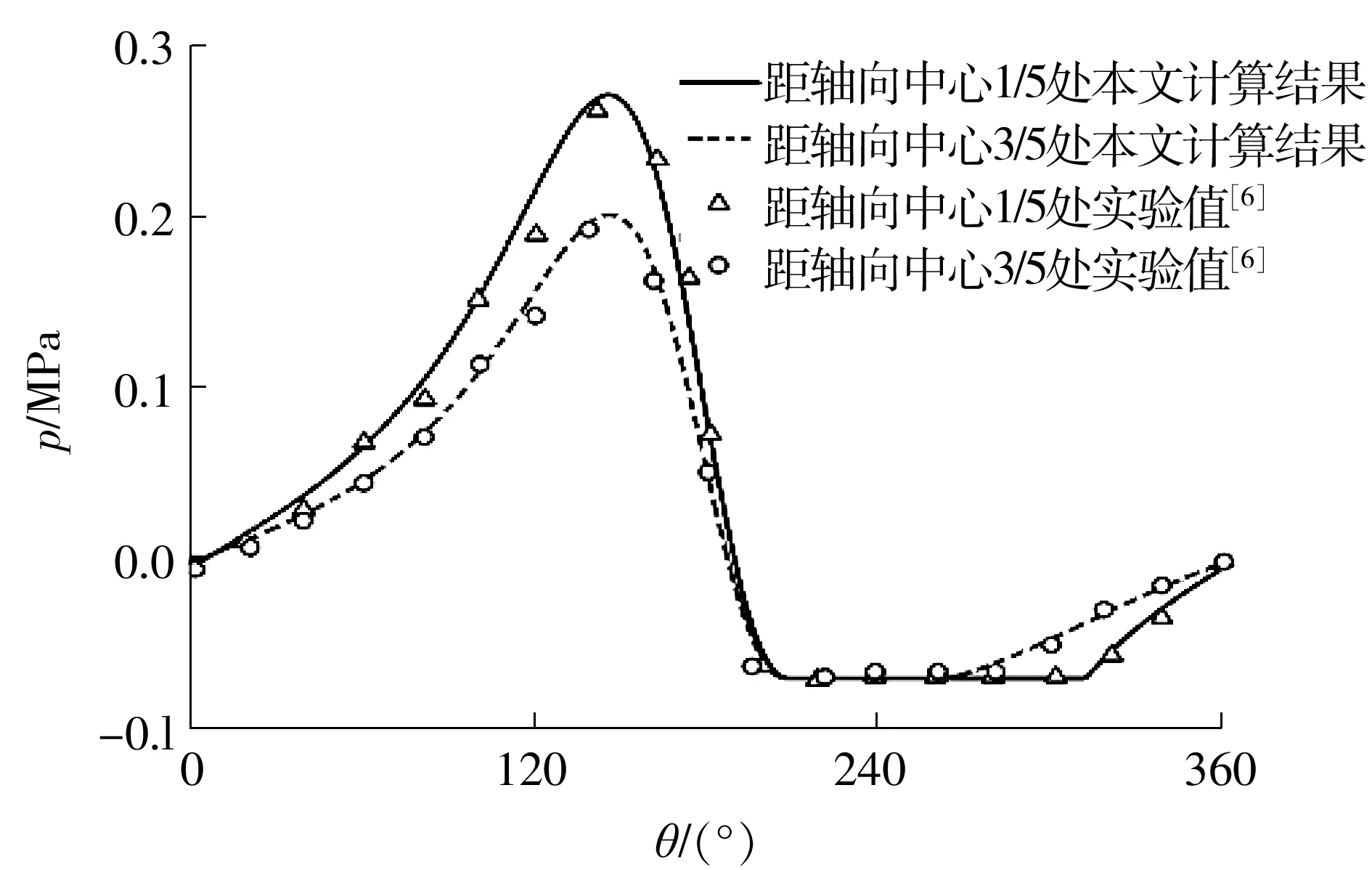
图3 理论计算和实验油膜压力分布比较

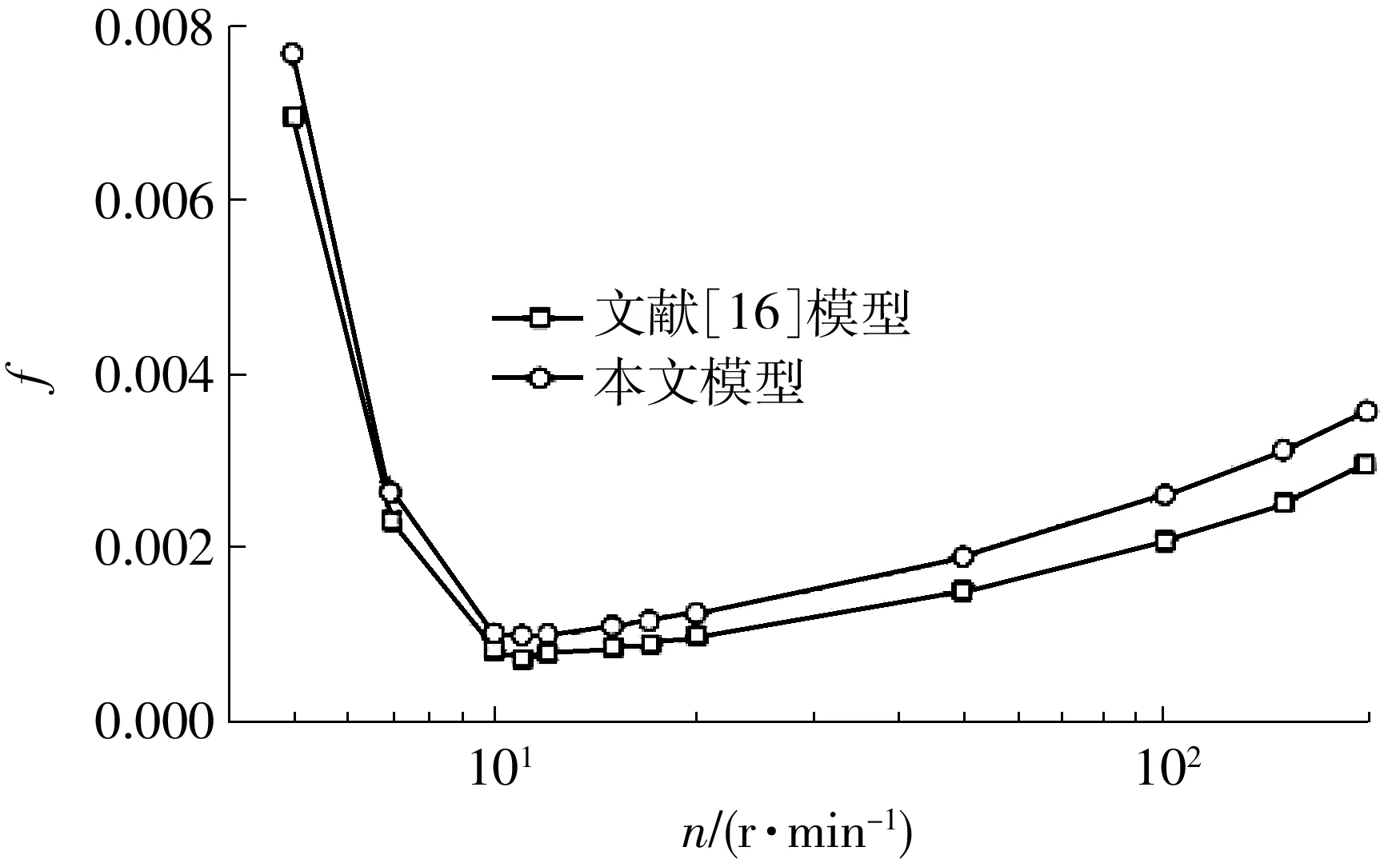
图4 不同模型的Stribeck曲线Fig.4 Stribeck curves of different models

2.3 网格无关性分析

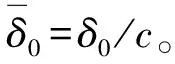
通常情况下，数值计算的网格数量对计算结果有重要的影响，过少的网格可能引起太大的计算误差，而过多的网格又会导致计算耗时长。因此，本文对轴承润滑进行了网格无关性分析。不同网格下的轴承混合润滑性能计算结果如表1所示，其中pmax为最大油膜压力。基于满足精度和节约时间的原则，本文计算采用了480×360的矩形网格。

表1 各种网格下的轴承性能计算结果

3 结果和讨论

3.1 磨损对膜厚的影响

图5为两种工况下不同最大磨损深度对轴承中截面油膜厚度分布的影响。由图中可知：磨损的发生导致油膜形状发生了显著的变化，高速工况尤为剧烈(见图5(b))，凸起形状破坏了油膜在收敛区的斜坡，且最小膜厚比减小，与文献[17]结果相符；在低速工况下，磨损使最小膜厚比增加，如图5(a)局部放大图所示，而在高速工况下则与之相反，如图5(b)所示。这是因为在低速工况下，膜厚比小于4，偏心率较大，轴承和轴颈发生接触，局部磨损使接触减少，进而增大了最小膜厚比，并且磨损使收敛楔变得缓和，有利于扩大流体动压力的作用区域，使最小膜厚比增大；而在高速工况下，偏位角大，磨损使间隙增大且收敛楔变陡，不利于扩大流体动压力的作用区域，导致轴颈下沉，最小膜厚比随着磨损深度的增加而降低，如图6所示。

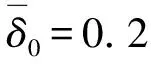
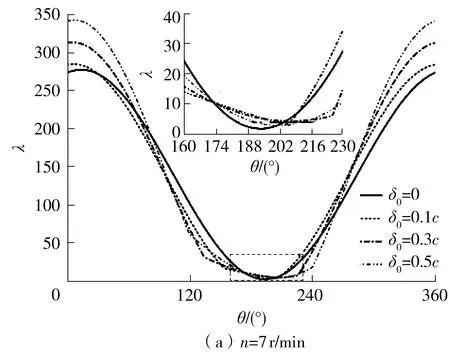
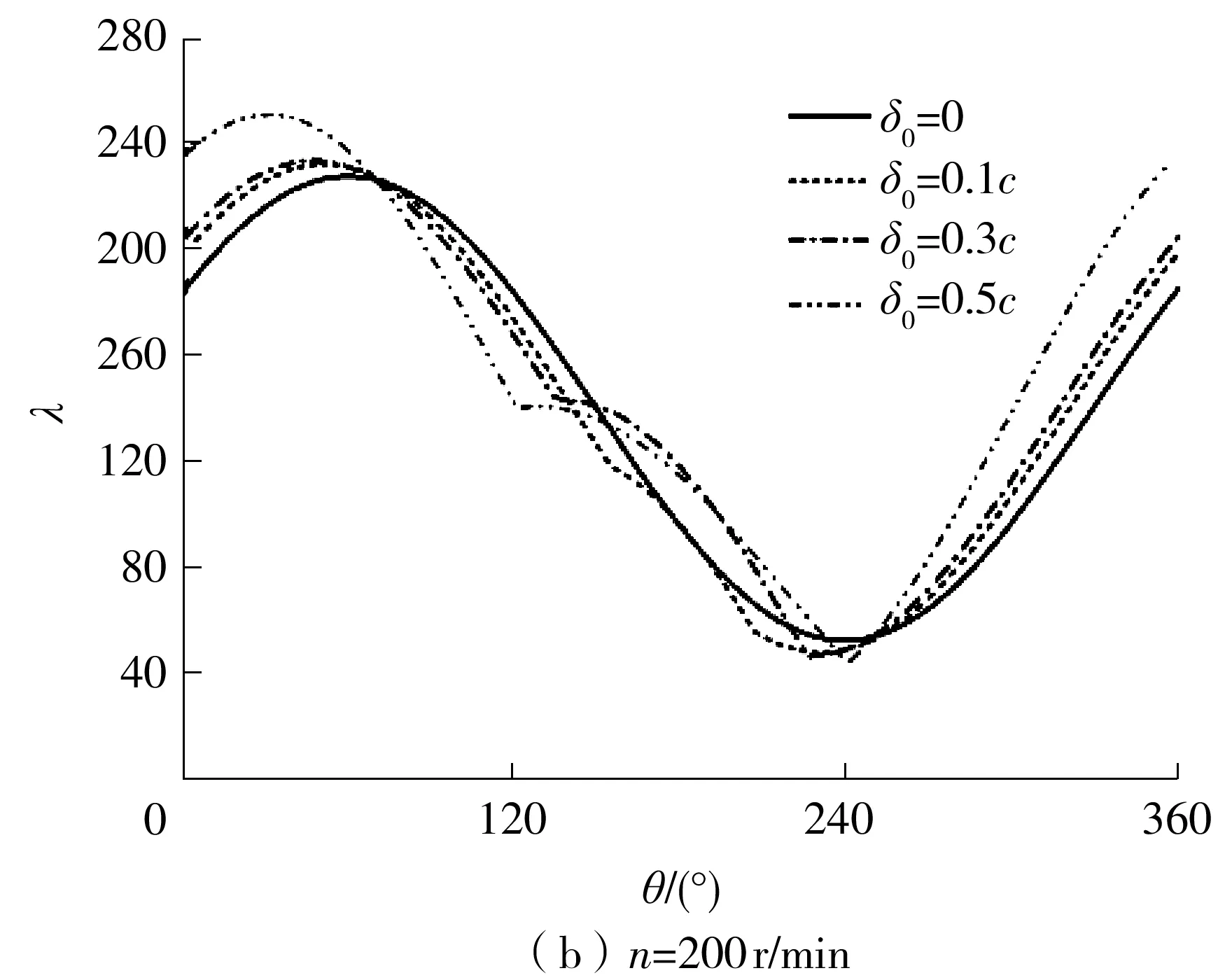
图5 最大磨损深度对轴承中截面油膜厚度分布的影响

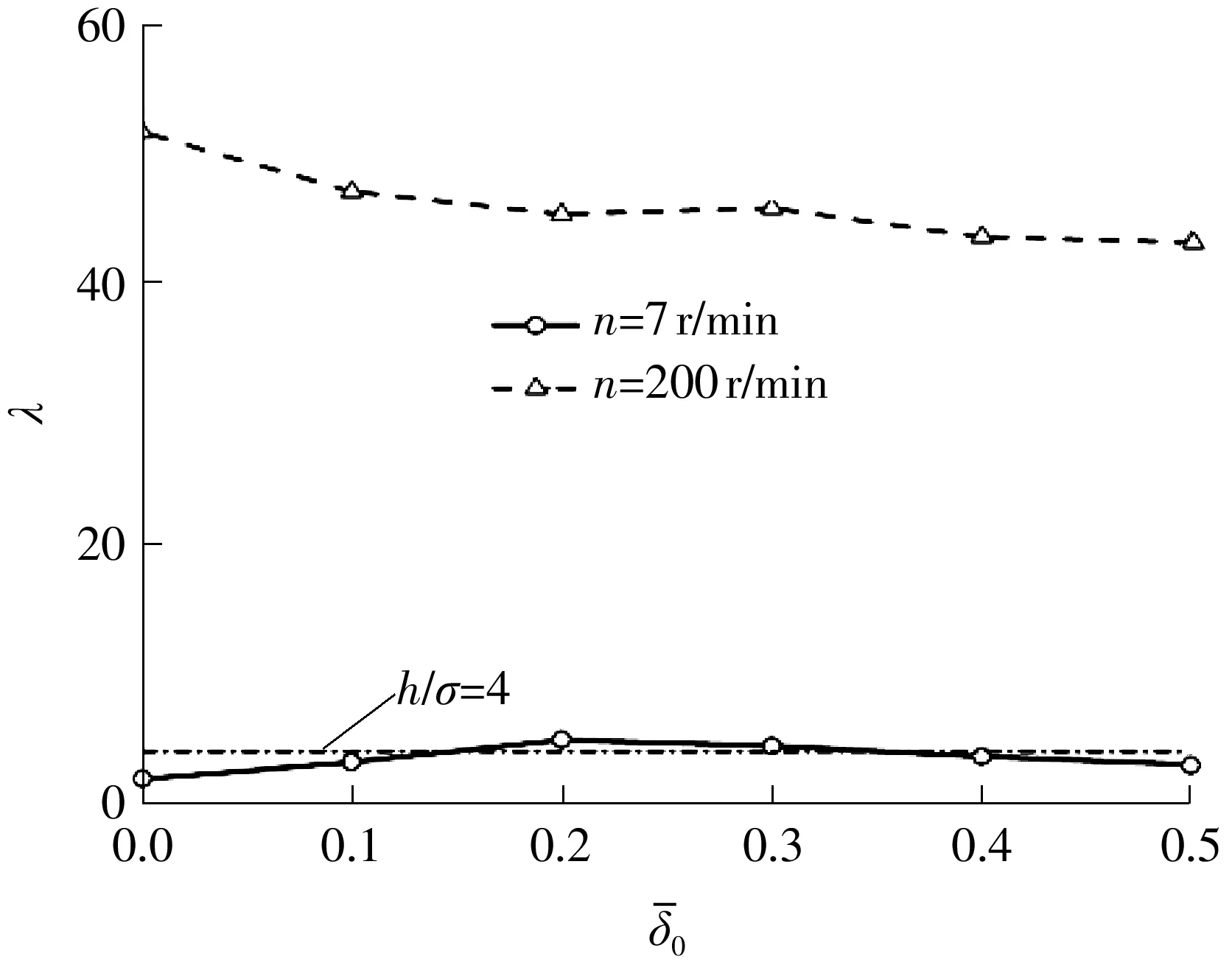
图6 最小膜厚比随相对磨损深度的变化

3.2 磨损对平均流体动压力分布的影响

轴承磨损后其平均流体动压力分布在不同工况下发生了不同的变化，如图7所示。在低速工况下，最大平均流体动压力随着磨损深度的增加先降低后增加，而在高速工况下则与之相反。这是因为在低速工况下，偏心率大，磨损使收敛楔变得缓和，扩大了流体动压力的作用区域(见图7(a))，使最大平均流体动压力降低；而在高速工况下，偏位角较大，磨损使收敛楔变陡，减小了流体动压力的作用区域(见图7(b))，使最大平均流体动压力上升，这与3.1节的结论相符。

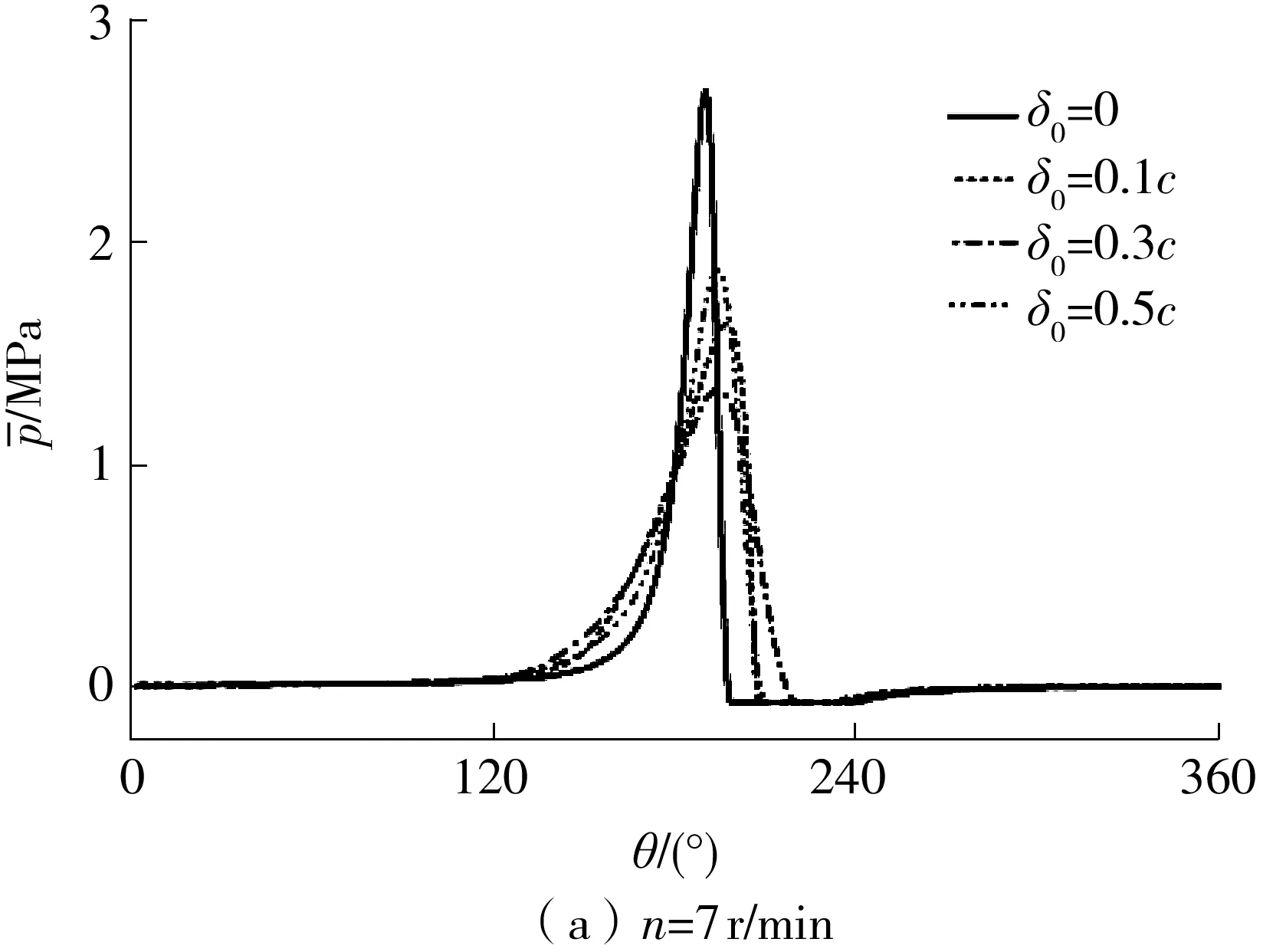
图7 最大磨损深度对轴承中截面平均油膜压力分布的影响

3.3 磨损对轴心位置的影响

图8为不同转速下轴承轴心的位置。由图中可知：随着转速的增加，偏心率减小，偏位角增大；当轴瓦最大磨损深度为0.1c时，与未磨损轴承相比，两者的轴心位置相近；随着磨损深度的增加，与未磨损轴承相比，磨损轴承的轴心位置相差越来越远，偏离原来的设计，且在低转速下，轴承下沉至磨损区域，偏位角减小，偏心率大于1。

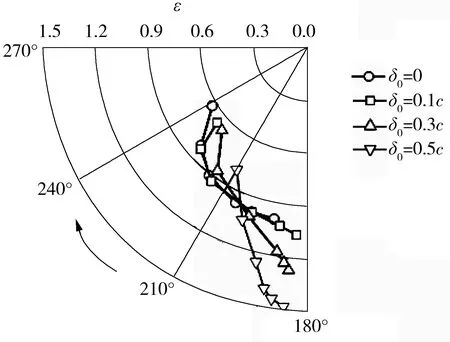
图8 轴承的轴心位置Fig.8 Position of axial center in the bearing

3.4 磨损对润滑状态的影响

Stribeck曲线用来描述摩擦系数与润滑状态之间的关系。图9为不同最大磨损深度下轴承的Stribeck曲线。在工程领域，摩擦系数最小的点被认为是混合润滑和流体动压润滑的转折点。根据这个标准，当轴瓦最大磨损深度分别为0.1c、0.3c、0.5c时，由混合润滑转向流体动压润滑的临界转速分别为6 、6和8 r/min。未磨损轴承的临界速度为11 r/min，说明不同的最大磨损深度均显著改变了轴承的润滑状态，适当的磨损有利于轴承快速实现流体动压润滑，而随着磨损深度的增加，需要更大的转速才能实现由混合润滑向流体动压润滑状态的转变。这是因为在小磨损深度下，扩展了流体动压力的作用区域，增加了油膜厚度，使微凸体接触载荷对摩擦力的贡献减小，因此在混合润滑阶段，

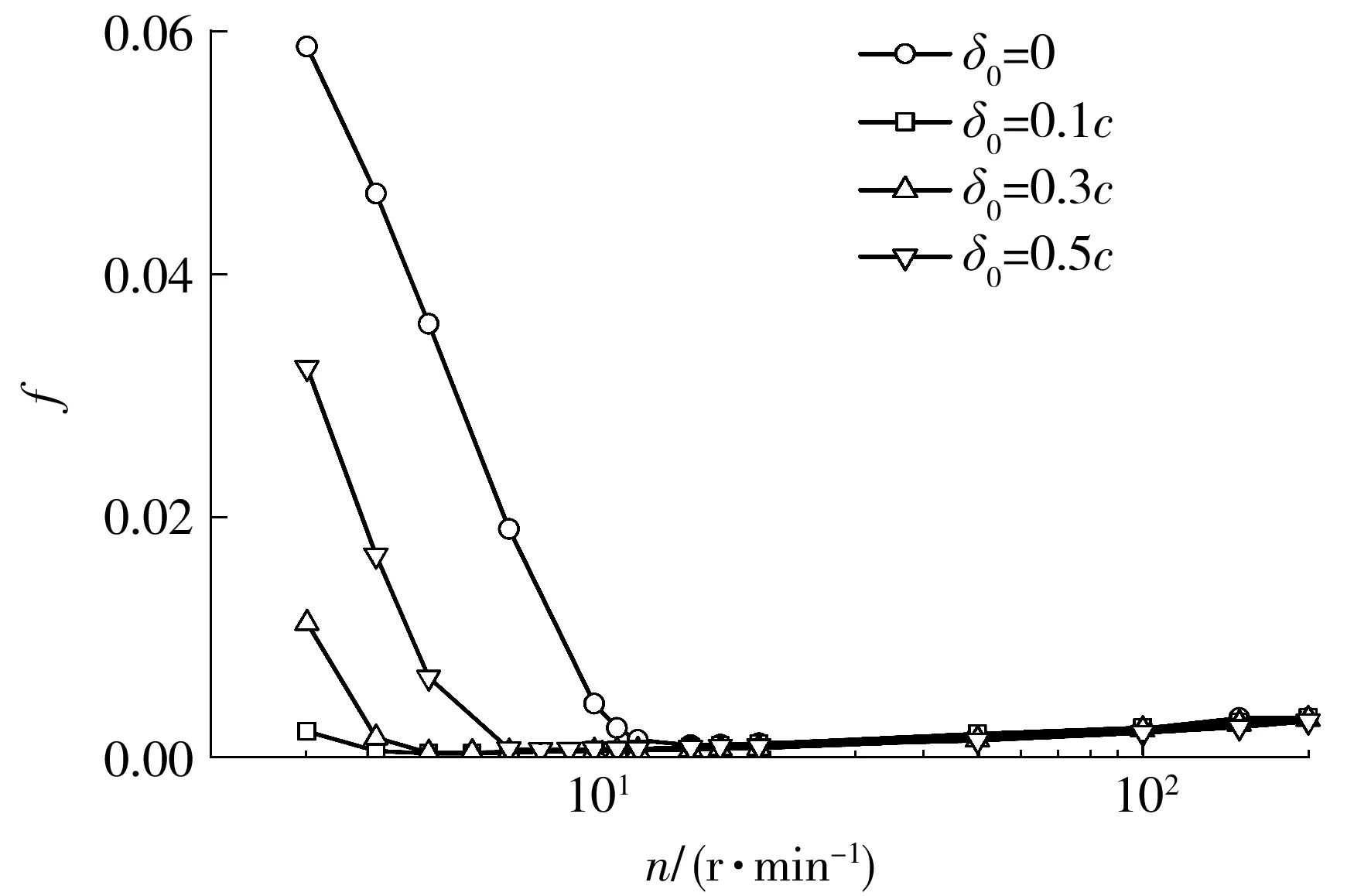
图9 不同最大磨损深度下轴承的Stribeck曲线

摩擦系数降低且能以较低的转速由混合润滑转为流体动压润滑。随着最大磨损深度的增加，摩擦系数逐渐上升，且需要更大的转速才能使轴承由混合润滑转为流体动压润滑，即最大磨损深度的增加逐渐对轴承润滑性能产生不利的影响。

4 结论

(1)磨损导致油膜厚度发生显著的变化，尤其在高速工况下。在低速工况下，磨损使最小膜厚比增大，而在高速工况下则与之相反。

(2)磨损改变了平均流体动压力的分布。在低速工况下，磨损使最高平均流体动压力先下降后上升，流体动压力的作用区域增加，而在高速工况下则与之相反。磨损深度的增加对轴承流体承载力逐渐产生不利的影响。

(3)磨损改变了轴心位置，使轴心偏离原来的设计。

(4)磨损使混合润滑阶段的摩擦系数先下降后上升。小磨损深度有利于降低混合润滑阶段的摩擦系数，且能以较低的转速实现由混合润滑转向流体动压润滑。随着磨损深度的增加，临界转速增大。