基于茶文化视角的中心极限定理的教学设计

熊 梅，张大林

（黔南民族师范学院数学与统计学院，贵州都匀 558000）

中心极限定理是概率论与数理统计中十分重要的定理，是概率论与数理统计课程教学中的一个重难点。中心极限定理的重要性在于，不管一个随机变量是离散型还是连续型，也无论这个随机变量服从什么分布，当这种相互独立的随机变量的个数增加时，其和的分布都趋于正态分布。因此，只要和式中加项的个数充分大，就可以不必考虑和式中的随机变量服从什么分布，都可以用正态分布来近似。然而，在实际教学过程中，由于中心极限定理本身的抽象性和结果的多样性使得学生易产生畏难情绪，导致学生很难准确深入理解中心极限定理的实质。

1 茶文化对创新思维培养的价值

对世界文化影响比较深远的中国传统文化中，茶文化是其中之一。茶文化包含了丰富的哲学思想，其中就有道家的“天人合一”及儒家“中庸”之道等优秀思想。所以，茶文化中能体现出遵循事物的发展规律，实现人与自然的和谐。这种和谐不是妥协适应，而是各个事物间能相互吸纳融合，使得各个事物间能以恰到好处的状态存在，并且达到一种平衡。茶文化中的这些哲学思想在对社会大众心智的启迪起着非常重要的作用。将茶文化的思想内涵渗透给学生，有利于他们在学习上能戒骄戒躁，踏实稳重，认真务实，树立正确的人生三观。同时，将茶文化的哲学思想融入到教学的各个环节中，可以促进创新培养新方式方法的诞生，对于提高学生的创新水平有着重要的意义。[1]本文在茶文化视角下，将教学设计与实验项目相结合，运用数学软件（如Matlab，Mathematic，Maple等）实现中心极限定理的仿真模拟，培养学生的学习兴趣，加深对定理的理解。

2 中心极限定理的表述

在一般的教材中，中心极限定理是一组定理：林德伯格（Lindeberg）-莱维（Levy）中心极限定理（独立同分布中心极限定理）、De Moivre-Laplace中心极限定理（二项分布的正态近似）和Liapunov中心极限定理（独立但不同分布中心极限定理）[2]。其中De Moivre-Laplace中心极限定理是独立同分布中心极限定理的特殊情况，而Liapunov中心极限定理则比独立同分布中心极限定理更具有一般性。

设Yn服从二项分布b(n，p)，引入随机变量Xk，在第k次试验中

De Moivre-Laplace中心极限定理设在独立试验序列中，事件A发生的概率，随机变量Yn表示“事件A在n次独立试验中发生的次数”，则对于任何实数x有下式成立：

独立同分布中心极限定理（Lindeberg-Levy中心极限定理）设随机变量相互独立，服从相同的分布，并且数学期望和方差都存在且方差不为0，即，则对于任何实数x有下式成立：

Liapunov中心极限定理设随机变量相互独立，且数学期望，方差，记。若Bn满足如下Lindeberg条件：存在δ＞0，使得n→∞ 时，有

3 中心极限定理的实验项目设计

3.1 数值近似实验项目

将所得的经验分布函数和正态分布函数的值列入下表。比较两个分布函数在相同点的值，发现它们的最大误差不超过0.06，说明用标准正态分布函数来近似Z的经验分布函数的效果还是比较好的。

F1000与 Φ0.1的比较

3.2 图形模拟实验项目

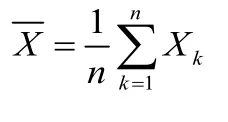
图1 样本容量n=1时的分布 图2 样本容量n=5时的分布图3 样本容量n=10时的分布

图4 样本容量n=20时的分布 图5 样本容量n=40时的分布图6 样本容量n=80时的分布

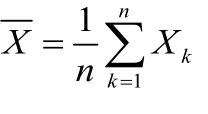
4 结束语

数学软件的使用，为中心极限定理的实验教学提供了便利.不仅对于抽象的中心极限定理，可以通过图形直观展示，加深学生对概念本质的理解.利用数学软件实施实验教学，既可以提高学生的学习兴趣和编程能力，还可以培养学生数学直觉和创造力，是一个不错的教学设计项目和实施方案.