用好数式通性，从“数”向“式”自然过渡

应佳成

摘  要：“式”是“数”的拓展与一般化，作为运算对象，对“式”的学习是真正的代数学习. 在教学中如何引导学生实现从“数”到“式”的自然过渡？笔者认为需要用好“数”与“式”之间的具体与一般关系，用好研究方式与研究结构的一致性，即用好数式通性，帮助学生从“数”的学习顺利过渡到“式”的学习. 对学生数式通性观念的培养是一个逐步渗透、逐步递进的过程. 文章从对“式”的认识、对运算律的遵循、对算理的理解和技能的落实、对代数体系的构建等不同发展阶段阐述如何实现从“数”向“式”的自然过渡，并提出了后续思考.

关键词：数式通性;迁移类比;运算能力

2020年10月20日，笔者有幸参加了由中国教育学会中学数学教学专业委员会、福建省教育学会数学教学委员会在福建建宁主办的“中央苏区、革命老区中学数学教师培训”活动. 活动中，浙江省杭州市富阳区永兴学校的毛大平老师（以下统称“执教教师”）开设了“整式”一课，以下是笔者从数式通性视角对式的教学展开的思考.

从本质上看，由于“式”是“数”的抽象，因此，在式的运算中，数的运算本质不变. 从数学的整体性来看，式的运算继承了“数”的运算的法则和运算律，与数的运算保持一致. 从思想方法来看，“式”是代数教学的开端，由于“式”是“数”的一般化，与“数”相比，既有继承也有发展，数式通性是在“式”的研究中具有统领地位的思想方法. 用好数式通性，从“数”向“式”自然过渡，让学生能够用看“数”的眼光看“式”、能够像运算“数”一样熟练地运算“式”，能够从认知上将“数”与“式”进行统一，能够建立初步的代数观念. 那么，如何实现自然过渡？如何体现数式通性？笔者认为，作为一种重要的数学思想，对学生进行数式通性观念的培养是一个逐步渗透、逐步递进的过程，本文将就此展开具体阐述.

一、理解“式”，用看“数”的眼光看“式”

从发展的角度看，用字母表示数是式的发展基础;从知识领域看，用字母表示数是数的进一步抽象，是更具有一般意义的数. 在小学阶段，学生已经知道用字母可以表示数，学习过用字母表示运算律，因此，学生对用字母表示数的学习并不是零基础的. 但这并不意味着学生有对“式”进行直接运算的能力，在对“式”进行运算之前，需要学生对“式”有充分的认识，从“数感”过渡到“式感”，对“式”有完备的认识，为运算打好基础.

1. 理解字母的运算逻辑

2. 明确“式”的构成要素的含义

由于数有运算单位，自然需要确定式的运算单位. 单项式是式的运算的最小单位，对单项式的构成要素本质的认识决定了整式的运算水平. 数式通性是认识单项式构成要素的重要思想，从单项式的结构中可以明确看出构成要素. 例如，5a3b表明它的运算关系是[5 · a · a · a · b]，但是此结构与多个因数相乘不同，数是个别的，a3b代表的是类型，是运算结构，系数（5a3b中的5）、字母（5a3b中的a3，b）是单项式的构成要素，说明单项式是式的运算的最小单位. 在以上认知过程中，教师需要帮助学生理解字母可以表示数，字母也可以用符合条件的具体的数来替换，这与数字因数是有差异的. 基于对数字因数和字母因数的对比与分析，发现式与数之间有继承、有差异. 式可以兼容数，是数的运算结构的一般化表示，从“数”过渡到“式”，明确“式”也是运算对象.

3. 用“式”抽象數量关系

随着学生对“式”的认识水平的提升，需要进一步培养学生抽象数量关系，并用“式”表示这些关系的能力. 例如，用归纳法表示简单的数列1，2，4，8，16，…，2n - 1的通项公式等. 在对这个问题的解决过程中，蕴含着“发现数的规律、用字母替换数、用式表示规律”等一系列思维过程，这都是从“数”向“式”过渡的良好载体.

二、遵循运算律，像算“数”一样去算“式”

整式的运算建立在数的运算基础之上，数的运算是式的运算的特殊情形. 但是初学阶段的学生缺少这样的整体视角，因而用好数式通性，帮助学生自然地实现从数的运算迁移到式的运算是学好式的运算的关键.

1. 用字母替换数，明确“式”可以算

整式的加减是融合数与式的学习、培育数式通性思想的最佳载体. 整式的加减运算的关键是合并同类项，在学习过程中要为学生设计合理的迁移机会，抓好思维发展的细微环节. 学生已经知道“式”是“数”的进一步抽象及推广，是运算对象，那么自然就会产生一个问题：“式”不等同于“数”，那么整式到底能不能相加减呢？因此，在整式的加减的教学时，要充分注意“式”与“数”的联系，类比数的运算探求整式加减运算的法则和规律. 例如，可以通过设计具有分配律结构特征的数的运算进行迁移. 第一步，先来计算如下三个算式：[22×5+78×5;] [22×52+78×52;] [22×5×6+78×5×6，] 显然，以上的运算利用分配律是非常容易完成的;第二步，将上述算式中的“5”和“6”换成其他的任意数，利用分配律依然可以顺利计算出结果，并且发现能够替换“5”和“6”的数有无数组;第三步，联想到用更具有一般性的字母表示数，将上述问题中的“5”换成“a”，“6”换成“b”，就此迁移完成[22a+78a，22a2+78a2，] [22ab+78ab]的运算.

在对“式”进行运算的初始阶段，要考虑到学生的学习是新旧知识相互影响与整合的过程，处理好从“数”到“式”的过渡，借助“字母表示数的意义”用字母替换数字，明确这样的“式”可以运算是非常重要的. 章建跃博士曾经做出阐述：从数字到字母，用字母表示数，其意义是使数学表达趋于抽象性、普遍性，对字母进行运算、推理所获得的结果是普遍成立的.

2. 分析运算律，明确“式”如何算

在前文阐述“式”能不能运算的过程中，已经交织着分配律的使用，事实上，“能不能算”与“怎样算”是相互交织的同一个问题. 在计算[22a+78a，] [22a2+][78a2，] [22ab+78ab]的过程中，离不开运算律，只有使用分配律，才能通过改变运算顺序将两个同类单项式合并，完成从“数”到“式”的学习迁移. 因此，教师要引导学生重点思考运算的依据，并利用依据对“式”进行运算，进一步归纳总结出合并同类项法则. 从数的运算到式的运算，运算法则和运算律的继承是运算得以实施的核心. 帮助学生类比迁移数的运算结构构建式的运算结构，是发展学生代数认知体系的关键环节.

在多项式加减运算学习之初，会有部分学生对于[2x2-5x-24x-3x2-2]这样的计算题不能理解，导致运算错误率较高. 究其原因，还是学生对新法则本质的不理解造成的，抓不住根本的运算规律导致已有基础和目标之间形成了差距，影响学习进程. 针对这样的问题，教师在教学中使用运算法则的同时要强调分配律所起的作用，并且不断强调算理，在每个步骤之后都强调运算本质，帮助学生将新法则化归为已有知识经验，在理解的基础上再进行运算，就可以有效解决问题.

再如，在整式的乘法中，多项式的乘法要利用分配律转化为单项式的乘法，而单项式的乘法又要利用交换律和结合律转化为幂的运算，各种式（整式、分式、二次根式）的运算都是在用运算律进行等价转换. 讲清楚这样的本质对于提升学生的数学整体观念非常重要.

三、“数”“式”统一，建立初步的代数观念

代数的基本精神就是灵活运用运算律去谋求问题的统一解法. 例如，有理数运算的关键在于弄懂算理，理解数的运算过程的实质;多项式的运算性质是数式通性最为直接的發展. 抓住数式通性也就抓住了从算术到代数过渡的枢纽.

我们知道，有理数运算是整个代数运算的基础，对有理数的研究过程（数−运算和逆运算−运算律−大小关系）提供了研究一个代数对象的基本思路. 因此，有理数的研究具有基础地位和作用. 基于对有理数运算基础地位的认识，教师需要边学习边构建研究框架，目的不仅仅是使学生学好有理数运算，更重要的是通过研究框架的构建，将代数知识条理化、系统化，为式的运算构建基础. 有理数的运算结构如图1所示.

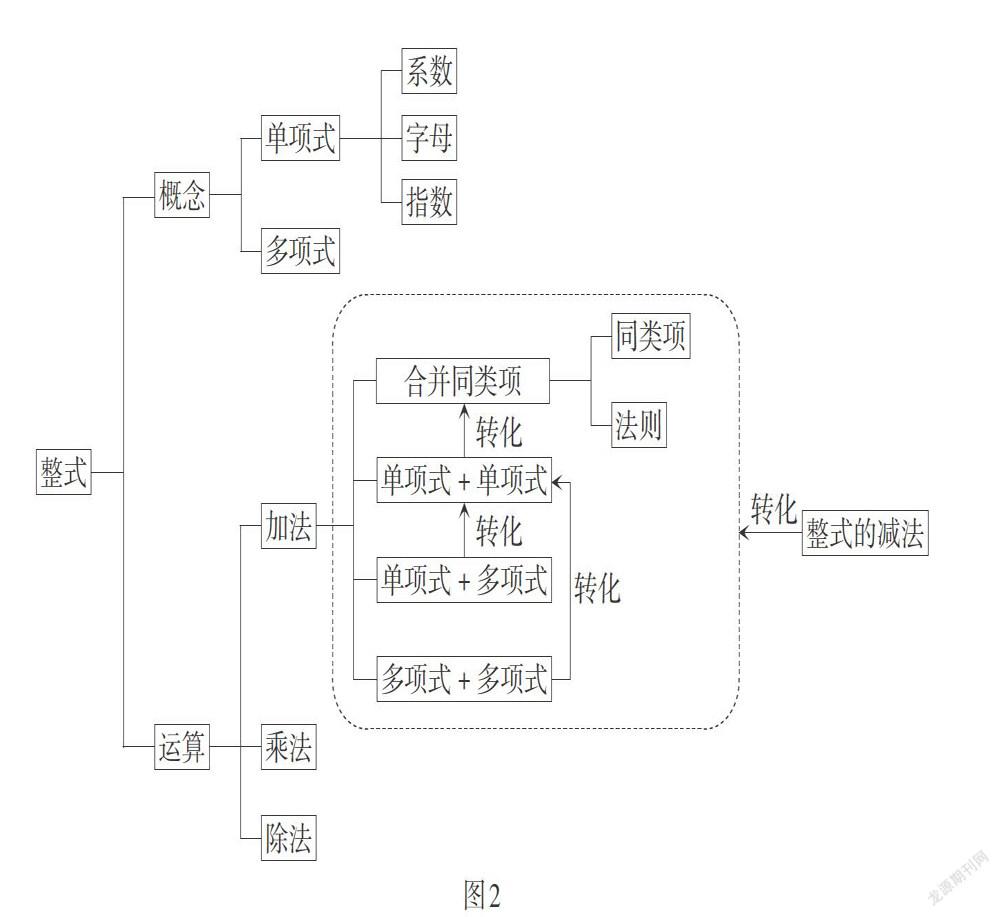
站在整体视角看式的学习，“式”与“数”在研究结构上是一致的. 从“数”拓展到“式”，尽管运算对象发生了变化，但是研究结构并没有发生实质性的变化. 概念和运算是两个主要研究的板块，加、减、乘、除是基本运算，利用相反数将减法统一成加法，利用倒数将除法统一成乘法，其根本都是运用了逆运算，这与数的研究也是一致的.“式”的研究结构如图2所示.

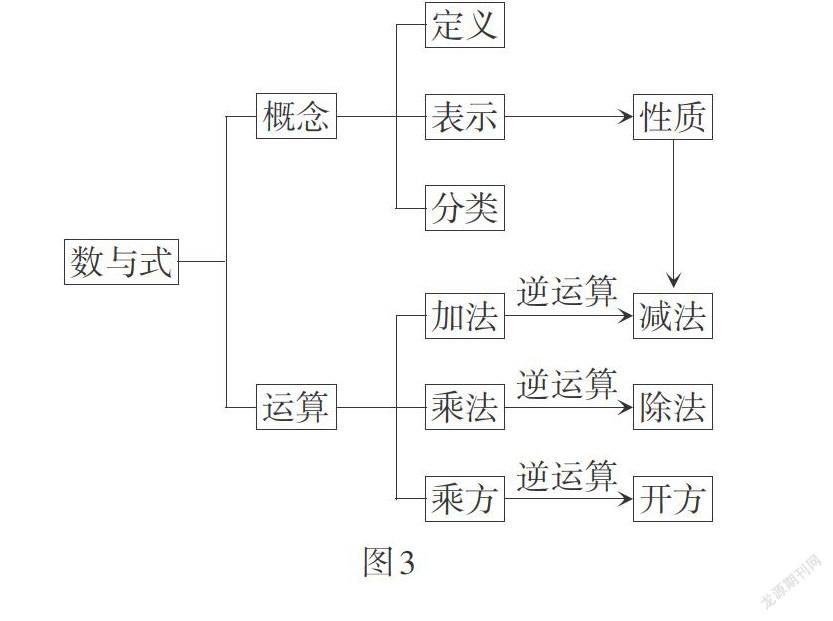
从数式通性的角度看，从数的运算扩展到“式”的运算，之所以研究结构没有发生根本变化，因为“式”与“数”的研究结构是高度抽象后的统一.《普林斯顿数学指南》一书中也指出，从长期看来，数学家慢慢放松“数”或“量”这些模糊的概念，而紧紧抓住代数结构这个比较形式的概念，到头来，每个数系无非就是可以在其上运行的实体的集合. 基于以上对比，将数与式的研究结构统一，如图3所示.

四、用好数式通性，发展学生的能力

1. 发展学生的运算能力

数学运算是解决数学问题的基本手段，运算的过程是演绎推理的过程. 式的运算能力是初中阶段需要发展的重要运算能力，培养式的运算能力有助于学生理解运算的算理，寻求合理、简洁的运算途径解决问题. 与数的运算一致，式的运算技能的落实需要在阐明原理的基础上规范思考、形成解决问题的基本步骤. 从能力培养层面看，步骤化操作中蕴含着运算技能的培养：运算对象的认识（如明确观察式子，划出同类项等）—运算方法的认识（如用运算律进行项的交换、结合等）—按步骤进行操作（得到运算结果）—形成自动化（思维和能力的提升）. 这样，学生面对一串算式，就能够明确每一步需要做什么，流畅的运算是对概念的进一步巩固，是对基础知识和基本技能的落实，是对思维的逻辑性的有益训练，使解决问题的过程更加有序. 从更高层次看，这是数式通性的更高水平的体现. 项武义先生在《基础代数学》中指出，在各种各样的代数问题中，我们总是运用各种代数运算（如加法、乘法等）来分析量与量之间的关系，系统、有效地分析代数问题中的量. 由于我们常用的数系运算律对于所有数字皆普遍成立，所以其做法都可以广泛地应用到任何一个只需用到那些数系运算律的代数系统（即可以假设所处理的符号满足数系通性）. 初中所学的多项式代数就是上述做法的一个典型例子.

2. 培养学生的迁移能力

整式的运算能力只是式的运算的起点，学生在整式学习中所获得的用数式通性研究问题的经验的迁移是更为重要的能力. 例如，在后续分式的学习中，数式通性同样发挥着重要作用. 分数与分式是具体与抽象、特殊与一般的关系，分式的概念、基本性质、约分与通分、四则运算法则，是从分数的概念、基本性质、约分与通分、四则运算法则中经过再抽象而产生的，根据这种关系，两者具有一致性，也可以说是数式通性. 因此，就可以确定分式单元从研究框架到具体研究过程，都是高度类比分数的研究完成的. 数式通性依然是自然、合情、合理地实现从分数向分式过渡的方法，整式的研究为其提供可借鉴、可类比的重要经验.

基于已有的认知经验去认识新的研究对象，学生的认知不会产生断层. 从心理学角度看，数式通性实质上是数的运算迁移或顺应，这种迁移既包括研究框架的迁移，也包括运算法则和运算律的继承. 现代心理学关于迁移现象的研究表明，如果学生在学习时，对学过的知识、技能和要领掌握得牢固，且又善于分析思辨，那么所学的知识、技能和概念会对另一种知识、技能、概念产生有益的影响和推动，这是学习的正迁移. 在教学中，有效利用正迁移的规律，有利于学生举一反三、触类旁通，发现“式”的研究方法.

3. 培养学生思考问题的方式

从更高的视角看，人的学习能力是不断发展完善的，用好数式通性统一代数问题的解决方式的过程，也是一种经验的积累，有助于学生形成数学方法与思想，学会有逻辑地思考问题，把握事物之间的关联和发展脉络，形成合乎逻辑的思维品质和理性精神，从而为其他知识领域的学习提供经验，真正提高学生的数学素养.

参考文献：

[1]TIMOTHY GOWERS. 普林斯顿数学指南（第一卷）[M]. 齐民友，译. 北京：科学出版社，2014.

[2]项武义. 基础代数学[M]. 北京：人民教育出版社，2004.

[3]章建跃，鲍建生. 深化课程改革，提高数学教育教学质量：暨第十一届初中青年数学教师优秀课展示与培训活动总结[J]. 中国数学教育（初中版），2020（4）：2-20.

[4]李海东. 承上启下，注重基础，做好算术到代数的过渡：人教版《义务教育教科书·数学》七年级上册介绍[J]. 中学数学教学参考（中旬），2012（8）：8-12.

[5]王红权. 理清教什么是怎么教的必要条件：谈合并同类项教学设计的要点[J]. 中国数学教育（初中版），2020（7 / 8）：14-18.