改进蜻蜓算法及其在特征选择中的应用

王万良，朱凯莉，李伟琨，赵燕伟，介 婧

(1.浙江工业大学 计算机科学与技术学院，浙江 杭州 310023；2.浙江工业大学 机械工程学院，浙江 杭州 310014；3.浙江科技学院 自动化与电气工程学院，浙江 杭州 310023)

0 引言

随着信息时代的到来，学习数据趋向于大规模、高维度，同时伴有复杂噪声，给模型的训练与学习带来了挑战。一个好的学习样本是训练分类器的关键，样本中的不相关或冗余信息会影响分类器的性能。因此，充分对数据进行分析挖掘来提取数据中的关键特征和潜在信息具有重要的研究价值和意义[1]。互联网、物联网等新一代信息技术在工业领域的应用使工业企业拥有的数据日益丰富，工业大数据应用因此得到更多关注。工业大数据是在工业领域信息化中产生的数据，这些数据中隐含着与工业生产制造相关的知识，合理地应用这些数据可以帮助企业提高效率、降低成本。工业大数据的典型应用包括产品创新、产品故障诊断与预测、工业生产线物联网分析[2]、工业企业供应链优化等。其中，产品故障诊断与预测通过监测生产流程中传感器的数据来分析整个生产流程，一旦某个流程偏离标准即可产生报警信号，从而尽快找到问题，减少损失。一个复杂的现代半导体制造过程通常通过监测从传感器或过程测量点收集的信号进行统一监管，然而并非所有信号在特定的监测系统中都具有同样的价值。测量信号包含有大量不相关信息和噪声，有用信息常常隐藏在其中，工程师们通常会得到大量冗余信号，如果将每种类型的信号视为一个特征，则可以应用特征选择来识别最相关的信号，然后使用这些信号确定导致生产线产量出现偏差的关键因素，这将有助于提高工艺产量，缩短学习时间，并降低单位生产成本。

特征选择旨在通过从大量原始特征中选择一小部分相关特征子集，消除无关和冗余的特征，来减少数据的维数，加快学习过程，简化学习模型。根据对特征子集的评价准则，可以将特征选择算法分为过滤式(filter)和封装式(wrapper)[3]。过滤式特征选择和后续学习(分类)算法无关，一般利用数据的统计性能评价特征快速排除非关键噪声，缩小优化特征子集搜索的范围，其计算简单、速度快、通用性好；封装式特征选择需要预设后续学习算法，使用选择的特征子集训练分类器，将分类性能作为特征子集的评价标准，该方法在速度上比Filter方法慢，但是其所选择的优化特征子集的规模相对小得多，非常有利于关键特征的辨识，而且准确率比较高，缺点是泛化能力较差，时间复杂度较高[4]。封装式特征选择由于其较高的准确率，是现在特征选择研究领域的热点之一。目前国内外研究主要集中在特征表示、搜索机制和评价函数上。在特征表示方面，为了降低搜索空间维数，Hong等[5]通过预设需要选择的特征数量，设计了一个二元向量来表示特征，其中预定义了一个数pd，将pd位二进制函数转换成十进制数作为被选特征的索引，从而将特征表示的总长度减少为pd与预设特征数量的乘积。在搜索机制方面，由于进化算法出色的全局搜索能力和较强的通用性，研究主要集中于通过改进各类进化算法来搜索特征空间。Zhang等[6]将骨干粒子群优化(Bare Bones Particle Swarm Optimization, BBPSO)算法结合最近邻算法应用于特征选择，并设计了一种强化记忆策略来更新局部最优粒子；Hsu等[7]用决策树进行特征选择,采用遗传算法(Genetic Algorithm, GA)寻找使决策树分类错误率最小的一组特征子集；Xue等[8]在粒子群优化(Particle Swarm Optimization, PSO)算法中引入初始化机制、个体最优更新机制和全局最优更新机制3种机制，所提改进算法在计算时间、特征数量和分类性能上均有提高。在评价函数方面，多数研究使用不同的方式将分类性能和特征数量组合成单个适应值函数，近期出现了很多将分类性能和特征数量作为两个单独的目标，引入多目标算法进行特征选择的方法，例如Tan等[9]将改进的GA与神经网络模型结合用于特征选择；Xue等[10]将多目标PSO算法引入特征选择并与其他流行的多目标优化算法、单目标方法进行对比分析，实验表明所提出的两种多目标PSO算法能获得更好的结果。另外，封装式特征选择算法也被广泛应用于各个领域，马玉敏等[11]选取支持向量机(Support Vector Machine, SVM)作为分类器，以二进制PSO优化算法进行特征选择，通过特征选择获得的动态调度策略分类模型实现了当前生产状态下的最优调度策略实时调度；Vieira[12]提出一种改进二进制PSO算法，在特征选择的同时优化SVM核参数，并将优化过参数的SVM模型应用于脓毒症患者的死亡率预测；Chiang等[13]将Fisher判别分析与GA结合,用于在化工故障中辨识关键变量，取得了较好的效果；Chen等[14]通过在SVM中引入余弦距离来消除分类器构造过程中的不相关或冗余特征，同时进行特征选择和SVM参数学习，构造了一种封装式特征选择算法，并将该算法应用于滚动轴承的故障诊断和阿尔茨海默病早期轻度认知障碍的诊断中；Chen等[15]通过GA和SVM构成特征选择算法，建立了商业危机诊断模型；Vignolo等[16]提出一个基于GA和K最近邻(K-Nearest Neighbor, KNN)的多目标封装式特征选择算法用于人脸识别，取得了较好的效果。

蜻蜓算法(Dragonfly Algorithm, DA)[17]是最近提出的一种新的群智能优化算法，该算法具有良好的全局搜索能力，已应用于各种优化问题，并取得了较好的效果。虽然DA在许多优化问题上表现良好，但是与大多数群智能算法一样均存在求解精度不高的问题，对此Sree等[18]提出一种具有记忆算子的混合DA，有效提高了DA的求解精度，但需要较大的迭代次数。

本文在DA的基础上结合序列浮动后向选择提高了DA的搜索精度，并结合KNN分类器提出一种封装式特征选择算法对半导体生产线各过程状态进行特征选择，以降低状态维度，确定生产过程中导致下游产量波动的关键因素，帮助提高产量并降低公司生产成本。另外，将所提算法应用于生产线机械手的动作识别，有助于提高生产线的安全质量和生产效率。

1 算法设计

1.1 基本蜻蜓算法

DA是由Seyedali Mirjalili于2015年提出的一种新型群智能优化算法，该算法主要学习了蜻蜓群体的两种行为模式——静态群体和动态群体，将这两种群体行为近似对应到群智能算法的全局探索和局部开发。在静态群体中，蜻蜓会分为几个子群体在不同区域飞行寻找食物；在动态群体中，蜻蜓会聚集成一个大群体沿着一个方向飞行。另外，可将蜻蜓的个体行为归纳总结为5种模式：①避撞行为，避免和邻近个体相碰撞；②结队行为，和邻近个体的平均速度保持一致；③聚集行为，向邻近个体的平均位置移动；④觅食行为，靠近食物源；⑤避敌行为，避开天敌。

在静态群体中，蜻蜓会聚集为一个小群体在小范围内来回飞行，并捕食小型飞行昆虫，该状态下蜻蜓的主要行为是聚集、觅食和避敌，其主要特征是飞行路径的局部移动性和突变性；在动态群体中，大量的蜻蜓会聚集成群，并往一个方向进行长距离迁徙[19]，其主要行为是避撞、聚集和结队，飞行路径的方向一致性是动态群体的主要特征。这两种群体中的蜻蜓个体均依靠5种主要行为更新其自身所在的位置。

食物所在位置和天敌所在位置分别从当前发现的最优解和最差解中选择。蜻蜓群体的飞行行为被认为是这5种个体行为的正确结合。为了在搜索空间里更新蜻蜓的位置并模拟其飞行行为，设置了步长向量(ΔX)和位置向量(X)。

步长向量

ΔXt+1=(sSi+aAi+cCi+fFi+eEi)+ωΔXt。

(1)

式中：s,a,c,f,e分别为蜻蜓5种行为的权重；Si,Ai,Ci,Fi,Ei分别为蜻蜓的避撞、结队、聚集、觅食和避敌行为向量；ω为惯性权重；t为当前的迭代次数。

当有邻近蜻蜓时，位置向量

Xt+1=Xt+ΔXt+1；

(2)

当周围无邻近蜻蜓时，定义蜻蜓的随机游走行为为

Xt+1=Xt+Le′vy(d)×Xt。

(3)

式中：d为位置向量维数；Le′vy为设定的飞行函数，由两个随机数和一个常数计算得到。

虽然DA对函数优化问题表现出了良好的性能，但是求解精度仍有待改善。因此，本文将改良的序列浮动后向选择(Sequential Backward Floating Selection, SBFS)算法加入DA来提高算法的开发能力，从而提高求解精度。

1.2 局部序列浮动后向选择机制

局部序列浮动后向选择(Partial Sequential Backward Floating Selection, PSBFS)机制的灵感来自SBFS算法。SBFS算法[20]是一种启发式搜索算法，搜索从全集开始，每轮在已选择的特征中选择一个子集x，使剔除子集x后的评价函数达到最优，再从未选择的特征中选择子集z，使加入子集z后的评价函数达到最优，如此循环直到选择的子集大小达到设定的要求。SBFS机制要从特征全集开始循环搜索，故而搜索速度慢，计算耗时，不适合特征数量较多的情况。PSBFS机制从DA当前搜索到的全局最优解而非全集开始搜索，删除能使删除后的判据值最大的特征，再添加能使判据值更大的特征，直到判据值不再增加，最后将新找到的更优解作为DA的食物源进入下一轮迭代。简而言之，PSBFS机制截取SBFS算法的核心步骤执行一次后向选择和一次前向选择后找到更优的解，将其更新为DA的食物源位置，在下一轮迭代时引导蜻蜓群体向更优的位置搜索。因此，PSBFS机制通过在DA找到的最优解附近搜索缩短了搜索过程，其作为DA的补充提高了算法的局部开发能力，使算法有潜力找到更优的解集，从而提高整个算法的求解精度。PSBFS机制的具体流程如下：

步骤1DA搜索得到的特征子集为Sk，k表示Sk中特征的数量，J(Sk)为子集的判据值，S为特征全集。寻找能使删除该特征后判据值最大的特征J(Sk-sd)>J(sk-s)，即从Sk中找出sd，使得J(Sk-sd)>J(Sk-s)，s为Sk中的任何一个特征。从集合Sk中删除sd。更新Sk-1=Sk-sd。

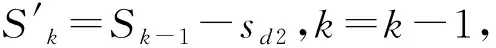
由于引入的PSBFS机制会增加计算时间，不利于大规模数据的特征选择，并不是每一代都引入PSBFS机制进行进一步搜索，而是设定控制参数决定是否在当前代引入PSBFS机制。

1.3 算法结构和流程

改进的蜻蜓算法(DA-PSBFS)在基本DA基础上，通过设置一个随迭代数递减的控制参数rc，随机在某些迭代中以DA当前搜索到的最优解为初始状态运行PSBFS机制，以增加DA的局部开发能力，从而提高算法的求解精度。r为一个0～1之间的随机数,当r>rc时，运行PSBFS机制在DA当前搜索到的最优解领域继续寻找更好的解；否则，跳过PSBFS机制直接进入下一代迭代。

(4)

式中Max-iter为算法的最大迭代次数。

算法框架如图1所示。

1.4 DA-PSBFS特征选择算法组成

改进的DA较好地兼顾了算法的全局搜索能力和局部开发能力，具有一定的优势。特征选择也是优化问题中的一类，因此将改进的DA作为搜索策略应用于特征选择，需要考虑特征的表示方式、初始化策略和评价函数的选择(包括评价指标和分类器的选择)等。

1.4.1 特征表示和初始化策略

特征选择是一个二元优化问题，特征子集以一个二进制向量表示，其中向量的长度基于数据集的属性数量。向量中的每个值都用0或1表示，1表示选择该属性，0表示不选择该属性。给定特征全集F={f1,f2,…,fN}，N为特征数量，于是特征子集可以用二进制向量表示为S{s1,s2,…,sn},si∈{0,1},i=1,2,…,N，si=1表示第i个特征fi被选择，si=0表示特征fi不被选择。在基本DA阶段，蜻蜓更新位置信息由步长向量与原位置向量相加得到，结果均为连续型数值，而特征子集的特征取值只可以是0或1。在不修改结构的情况下，将连续数值转换为二进制值有效且易实现的方式是转换函数。转换函数将步长信息作为输入量，输出为0或1。本文采用的转换函数为[17]。

(5)

由此，蜻蜓个体的位置更新公式为[17]

(6)

种群初始化时个体各维位置的取值为一个0～1间的随机数r，r>0.5则该维特征取1，r≤0.5则该维特征取0，从而在初始得到一个随机的特征子集。

1.4.2 评价函数

特征选择可以被认为是一个多目标优化问题，存在两个相互矛盾的目标：最少的选定特征和更高的分类精度。选择的特征数量越少，分类精度越高，解决方案越好。分类精度是将选择的特征子集作为分类器输入训练分类器，再用分类器对测试数据集进行分类后计算得到的分类准确率。为了平衡每个解中选择特征的数量(最小)和分类精度(最大)，采用线性加权的方式将两个目标组合成一个单目标函数[21]，即

(7)

式中：Acc为分类器分类正确率，这里使用KNN分类器；|S|为特征子集中特征的数量；N为数据集的特征数量；α，β为两个权重系数，分别对应分类质量和子集大小的重要性，α∈[0,1]，β=1-α。

2 实验仿真

2.1 数据集选择

算法实现均在Dell PowerEdge R930(24盘)服务器上完成，其核心配置包含多个Xeon E7-4820V4*2型号的CPU。为了评估所提方法的性能，实验在来自UCI数据库的9个特征选择基准数据集上进行。表1所示为所用数据集的详细信息，包括每个数据集中属性和实例的数量。

表1 实验数据集列表

2.2 实验结果

2.2.1 DA与DA-PSBFS对比

PSBFS算法在基本DA当前找到的最优解附近搜寻更优解，可能影响到算法的收敛速度。因此，以Congress和Ionosphere数据集为例，图2所示为所提算法与DA在搜索过程中随迭代次数的增加而变化的适应值曲线，其中适应值函数综合了分类精度和特征子集的特征数量。

从图2a可见，原算法在21代时收敛于0.055，改进算法于63代时收敛于0.037，引入的PSBFS虽然使算法收敛更缓，但是找到了更优解。图2b中，改进算法在48代收敛于0.064 5，原算法在73代收敛于0.070，改进算法更早收敛，这是由于改进算法在前期仍然有可能执行PSBFS机制找到更优解，引导算法向更优的区域搜索并收敛。

为了检验所提PSBFS算法对DA开发能力的影响，表2列出了加入PSBFS前后所得的实验结果，包括分类精度和所选择的特征数量，结果均为5次实验的平均值。其中，α=0.99,β=0.01,Max-iter=100。

表2 加入PSBFS前后对比分类精确度、被选的平均特征数及计算时间

续表2

2.2.2 与其他进化及群智能算法对比

为了测试所提算法的整体能力，将改进DA与当前流行的群智能算法和进化算法进行对比。其中，ABACO(advanced binary ant colony optimization)[21]是一种改进的二进制蚁群特征选择算法，在特征选择问题中有良好的表现；GA和PSO均为经典的进化和群智能算法；二进制骨干粒子群优化(Binary Bare Bones Particle Swarm Optimization, BBBPSO)算法[22]、蚁狮算法(Ant Lion Optimization, ALO)[23]和带有模拟退火的鲸鱼优化算法(Whale Optimization Algorithm with Simulated Annealing, WOASA)[24]分别是2015年和2016年提出的新型群智能算法，在各类优化问题上均有良好的表现，并在特征选择领域得以应用。

表3和表4分别从分类准确性和所选特征数量两个方面与当前流行的进化和群智能算法(ALO,GA,PSO,WOASA)在上述9个数据集上的表现进行比较。实验设置的种群数量均为60，最大迭代次数均为100次，分类算法K=5；ABACO和BBBPSO算法额外的实验参数均采用文献中的设置；实验结果为5次实验的平均值。Full列出的是用特征全集进行分类得到的分类精确度。

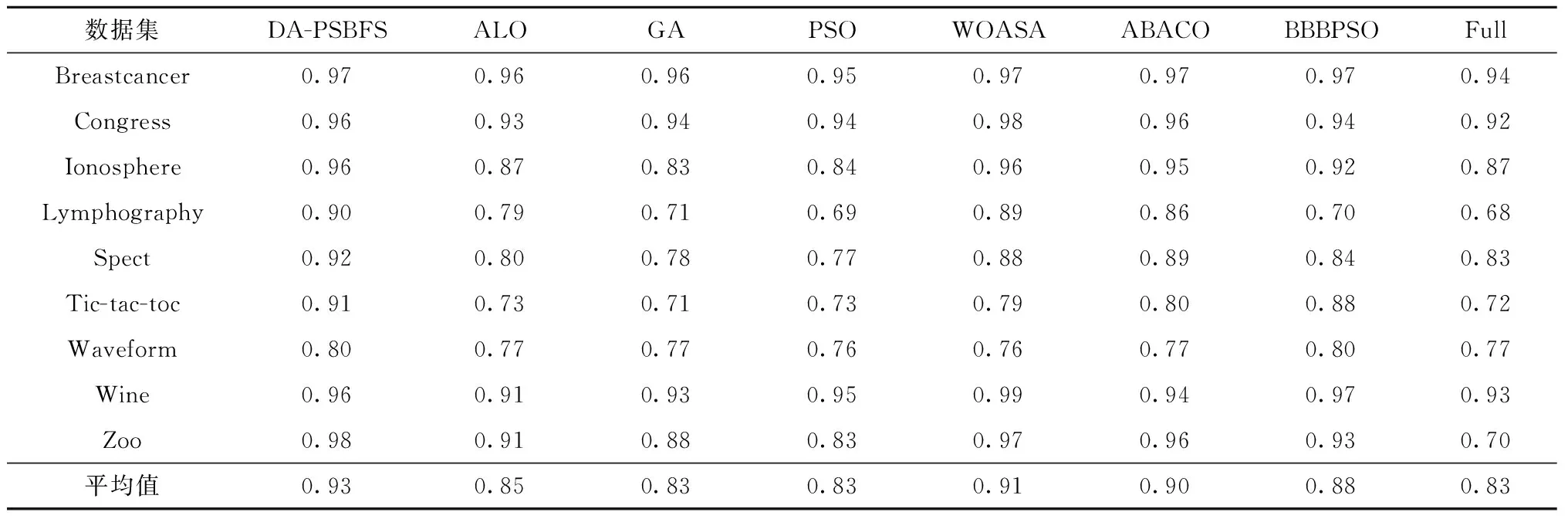
表3 平均分类精确度与其他进化及群智能算法对比

表4 平均选择的特征数量与其他进化及群智能算法对比

由表3可知，所提算法在上述所有实验数据集上的分类性能均优于ALO,GA,PSO算法，在7个数据集上较优于WOASA和ABACO，在6个数据集上较优于BBBPSO。另外，所选择的特征子集训练的分类器的分类精度明显优于基于特征全集训练的分类器，证明算法通过特征选择减少了不相关和冗余特征的影响，提升了分类器的性能。图3直观地展示了所提出算法较对比算法在分类精度上的优越性。

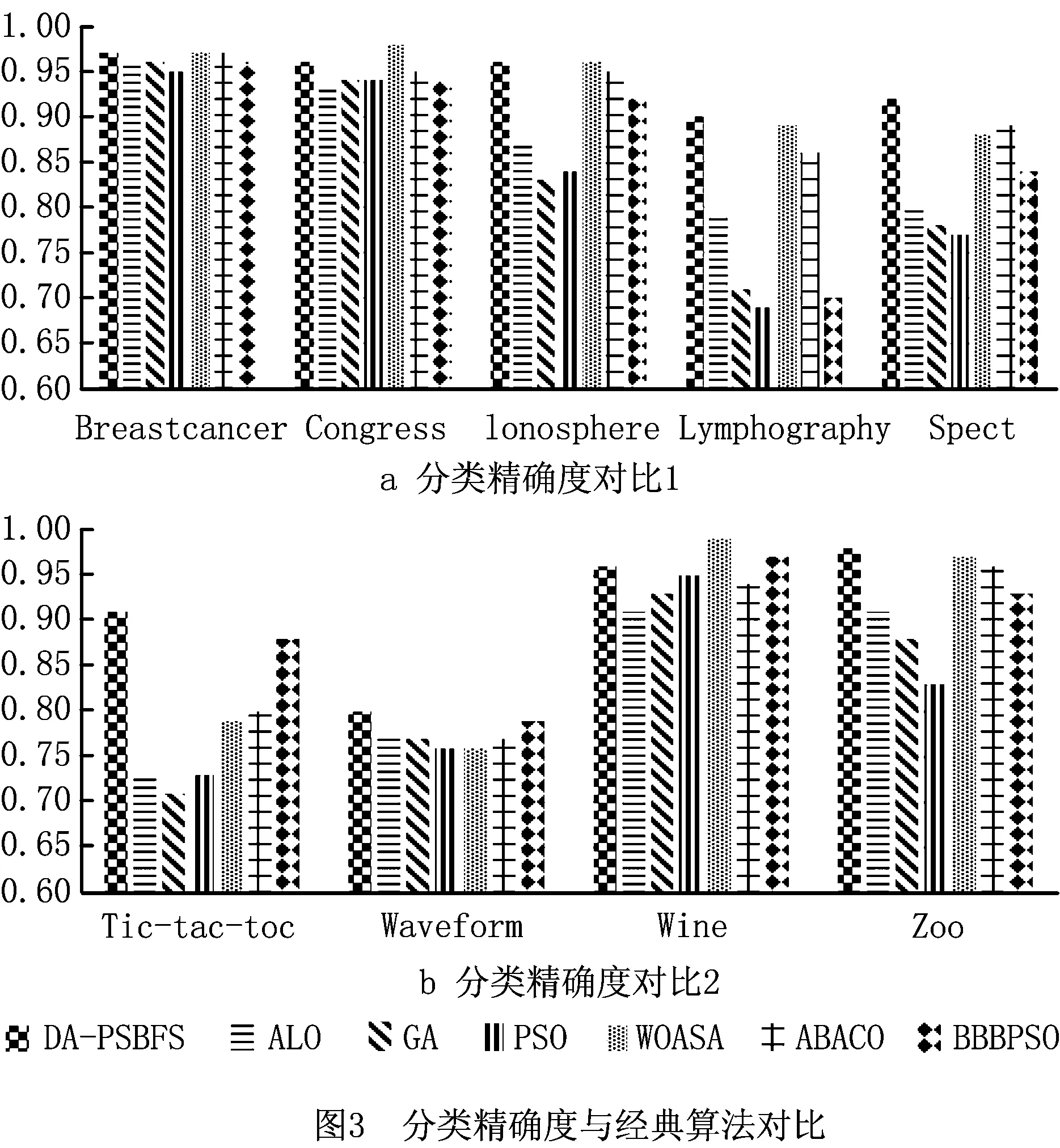
表4所示为用于测试的数据集所包含的特征和实例数，并给出了所提算法与当前流行的算法运行5次取得的平均特征数量，最后列出了在所有测试数据集上分别运行各算法后选择的特征数量平均值。

由表4可知，所提算法在5个数据集上取得了最小的特征数量，在余下4个数据集上选择的特征数量接近最好结果。从总体平均值可以发现，所提算法寻找的特征子集最精简，总体表现优于所有对比算法。由此证明所提算法能够高效完成特征选择，降低数据维度，简化学习模型。

2.3 实例应用

通常通过监测从传感器或过程测量点收集的信号，可以对复杂的现代半导体制造过程进行统一监管，然而并非所有信号在特定的监测系统中都有价值。测量信号既包含有用信息，又包含大量不相关的信息和噪声，识别其中的关键特征有利于提高生产效率、降低成本。以本次实例的数据集为例，该数据集来源于SECOM公司的半导体生产线，其中包括1 567个实例，每个实例代表具有591个相关测量特征的单个生产实体。标签表示内部线路测试合格与否，-1表示合格，1表示不合格。在该数据集上应用所提出的特征选择算法各运行10次，实验结果如表5所示。

表5中列出了10次运行结果的中值、最好值、标准差及选择的特征数量。可见，所提特征选择算法兼顾较好的分类精确度和较精简的特征数量，其精确度中值均优于对比算法，精确度最好值优于GA和PSO算法，接近最优的WOASA；在选择的特征数量指标上，所提特征选择算法优于所有对比算法。通过算法确定了导致生产线产量波动的关键信号，对这些信号进行监测有助于提高工艺产量并降低单位生产成本。

表5 SECOM数据集结果

另外，生产流水线上常配备机械手参与生产装配，对机械手进行监测可以快速定位问题。考虑到半导体生产线的装配速度较快，尽早发现异常并做出修正能较在大程度上保证生产安全高效。以下是一个机械手的数据集，该机械手可以完成5种动作，因此用5个标签标记这5种动作。数据集中记录了7万个实例，每个实例包含36个特征。应用所提算法对该数据集进行特征选择，实验结果如表6所示。

表6列出了10次运行结果的中值、最好值、标准差及选择的特征数量。可见，所提算法的分类精确度中值高于所有对比算法，最好值也接近最优。通过算法能够确定判断机械手动作的关键特征，重点关注关键特征有助于提高生产线的安全系数和生产效率。

表6 机械手数据集结果

3 结束语

本文提出基于改进DA的特征选择算法，将改进的PSBFS与基本DA融合，在DA当前发现的最优解附近进行局部搜索，从而提高DA的开发能力。工业大数据中隐含有与工业生产制造相关的知识，合理地应用这些数据可以帮助企业提高效率、降低成本。由此，将所提算法应用于生产线数据特征选择，基于分类精度和所选的特征子集大小两个指标，将本文算法与封装型特征选择算法中最相关的算法进行了对比分析。根据实验结果，所提算法在两个评价指标上均较优于对比算法，而且特征选择对分类效果影响显著，缺点是计算时间相对更长，当数据量极大时很难进行实时动态调整。因此，下一步的研究目标是考虑更高效的特征表示方式或先进行过滤式特征选择的混合方法，从而降低计算时间，以应用于更大范围的特征选择问题。