考虑剔除虚假云服务的制造云服务优选
2020-09-10江泽豪伊德景朱光宇
江泽豪,伊德景,朱光宇
(福州大学 机械工程及自动化学院,福建 福州 350116)
0 引言
随着云制造平台的快速发展,吸引了大量云用户和制造商,云池中的云服务急剧增多,但质量水准参次不齐,其中不乏一些虚假的制造云服务,恶意竞争的制造商通过发布虚假信息、提供虚假的服务评论和供应厂商来迷惑云用户,不但伤害了云用户的利益,而且危害了其他制造商的权益。因此,制造云服务的可信度评估、虚假云服务剔除及在此基础上的制造云服务优选成为本领域研究的焦点。
马文龙等[1]提出一种基于服务质量感知的云服务选择模型,通过评判不诚实评价信息来评价服务质量,为用户选择最佳云服务;陶飞等[2]对制造云服务进行可信评估,并对服务进行组合搭配;魏乐等[3]选择5个因素衡量云服务的可信度,并采用加权平均的方法计算制造云服务的可信值;马华等[4]定义了云服务的个性化特征,利用相似度函数识别特征共同体,通过个性化特征加权值来评估可信度;李超[5]建立了一个多指标评价模型对云服务的可信度进行评估;刘钻石等[6]通过选取6个制造云服务指标作为可信特征集,提出基于D-S(Dempster-Shafer)理论的云服务评价方法;Chiregi等[7-8]利用拓扑衡量方法完成云服务综合可信评估;Singh等[9]搭建了多维信任评估系统对云服务进行选择。
云制造环境下,针对制造云服务有效性和综合质量评估的研究是建立在云平台上存在大量可靠且真实的制造云服务,而实际上有些制造云服务存在虚假行为,通过文献分析可知,现有文献对剔除或识别虚假云服务的研究较少,或者对虚假云服务的识别程度较小甚至并未识别虚假云服务,有关虚假云服务的识别仅依赖于用户的反馈。
本文以商业化运营的工程机械交易云平台“铁臂商城”作为数据源,采用3个步骤进行基于虚假云服务剔除的制造云服务优选:①基于蒙特卡洛模拟估计超体积的虚假云服务剔除;②建立基于遗传算法(Genetic Algorithm, GA)的模糊c均值聚类算法(Fuzzyc-Means algorithm, FCM)进行制造云服务可信度评估,结合层次分析法(Analytic Hierarchy Process, AHP)和熵值法提出云服务组合赋权综合评价模型来计算云服务综合评价值;③将云服务的可信度等级与综合评价值结合,对云服务进行优选排序,得到最佳制造云服务。
1 数据获取与量化
“铁臂商城”是行业内首家网上购置工程机械的交易平台,聚集了国内外工程机械大小品牌的各种型号,其种类丰富、型号齐全,经过多年运营,积累了庞大的客户交易量。
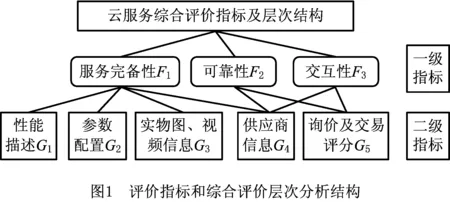
为了获取平台上不同数据类型的云服务信息,本文针对该平台开发了一个网页爬虫,通过网页爬虫爬取特定位置所需的云服务信息。分析平台上影响云服务可信度评估和质量综合评价的因素,确定爬取每个云服务的10项信息,将10项信息归类为云服务ID和5项评价指标。品牌和型号为云服务ID,5项评价指标分为两级,一级指标分别为云服务的完备性、可靠性、交互性,二级指标包括云服务性能描述、云服务参数配置、服务提供者的实物操作图或视频描述,供应商信息,询价和交易评分信息。图1所示为评价指标和综合评价层次分析结构图。
上述信息需要采用不同的处理方式转化为定量指标才能用于后续云服务的识别、评价和优选。不同指标的量化方式如下:
(1)性能描述信息 平台上对每一个云服务性能的描述差异较大,因此本文以性能描述的详细程度对其进行量化。描述云服务的字数越多,详细程度越高。例如针对挖掘机,随机抽取爬取数据的50个样本,计算描述性能的字数,通过主观评判将性能描述信息量化为0~100之间的数,并分为五段数值。量化公式为:
z1(w)=
(1)
式中:z1为云服务性能描述信息量化的数值;w为性能描述的字数。5个分段区间临界值通过计算取样值得到。
(2)参数配置信息 对参数的项数进行量化。由于工程机械自身的性能参数较多,云服务的参数项数越多,对云服务描述得越详细,云服务的综合质量越好。将参数配置项数量化为0~100之间的数。量化公式为
(2)
式中:z2为参数配置信息量化的数值;e为某云服务参数的项数;emax和emin分别为某类工程机械在云平台上参数项数的最大值和最小值。
(3)实物操作图或视频描述信息 以提供的实物操作图(视频)的多少作为量化依据,将操作图(视频)数量从0~5(含>5)张(个)对应不同量化值,对应的量化数值z3=0,20,40,60,80,100。
(4)供应商信息 供应商对云服务能否达成交易起重要作用。将云服务的供应商数量化为0~100之间的数,量化公式为
(3)
式中:z4为品牌供应商信息量化的数值;A为某云服务供应商的数量;Amax和Amin分别为某工程机械云服务供应商数量的最大值和最小值。
(5)询价和交易评分信息 该项信息包括询价数量、评价总人数、交易的平均评分、有效评价个数和平均询价时间。平台上的这些信息为量化数据,可借鉴式(2)将其量化到0~100之间,取平均值作为询价和交易评分的数值z5。
2 虚假制造云服务的特点和剔除方法
2.1 虚假制造云服务的特点
通过分析平台数据总结归纳认为,虚假制造云服务信息分化严重,特点有:①制造云服务提供的基础信息(包括性能属性、参数配置和实物操作图)不全或无相关信息内容。例如,在无基础信息的情况下,拥有比较高的平均评分、较多的询价数量,且评论都是一边倒的好评。②基础信息完备,但无交易人数和交易评分,而且没有供应商信息等。由于虚假制造云服务涉及多个评价指标,评判虚假制造云服务需要综合考虑多个指标因素。
2.2 基于蒙特卡洛模拟估计超体积的虚假云服务剔除方法
选用超体积(hypervolume)作为衡量多个因素的综合指标,计算每个云服务多维指标的超体积值,根据超体积值识别虚假制造云服务,并将其剔除。计算过程中超体积方法考虑了解集的收敛性、均匀性和广泛性[10],因此特性优良。
本文所建的云服务评价指标体系为高维数据,包括5个指标(5维数据),而且每个云服务的多维数据必然存在超体积值。通过比较其云服务的超体积值与选定的标准超体积来判断云服务的数据是否达到标准,以此识别云服务的真实性。超体积算法不但可以综合分析多个指标属性,而且能够通过异常结果发现两极分化现象[11]。
由于超体积算法在高维空间中的计算时间太长[12],本文选择基于蒙特卡洛模拟估计的超体积算法计算云服务评价指标的超体积值,蒙特卡洛模拟估计能够从已知概率分布抽样建立各种估计量。文献[13]证明,该算法设定的采样点越多,计算的估计值越接近准确值,而且用时较少。
采用基于蒙特卡洛模拟估计计算云服务评价指标的超体积过程如下:
P={P1,P2,…,Pk,…,Pn}为包含任意n个制造云服务的集合,S∶{(z1,z2,…,zj,…,zM)∈P|∀1≤j≤M,lj≤zj≤uj}为云服务的评价指标,其中:M为云服务评价指标的个数(维数),zj为指标值,uj和lj分别为指标的上下限。所有指标形成的多维空间最大体积
(4)
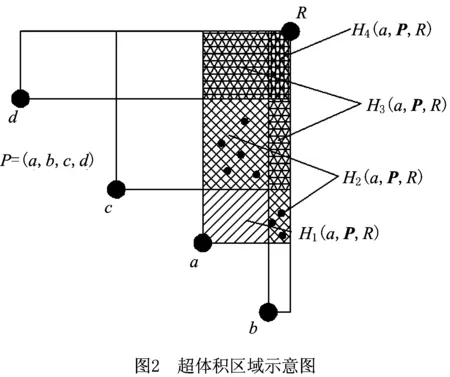
定义1a为某云服务指标在评价指标多维空间中代表的一个点,P为云服务集合,R为参考点。将P中所有云服务评价指标投影到二维平面,表现为点,如图2中的点a,b,c,d所示,a点与参考点R形成的矩形与其他点形成的矩形有交集,用H(a,P,R)表示a与参考点R所围成矩形区域,Hh(a,P,R)表示a与参考点R所围成矩形的第h个区域。图1中,H(a,P,R)是所有阴影构成的矩形,由H1(a,P,R),H2(a,P,R),H3(a,P,R),H4(a,P,R)组成。
超体积算法需预先设定参考点R,则云服务集合P与参考点R构成一个评价指标多维空间,n个云服务点P1,P2,…,Pn随机分布在多维空间中。运用蒙特卡洛思想,计算n个云服务在各区域中的分布数量占总云服务数量的比值,用该比值和总体积计算各区域所占的体积。判断云服务评价指标点Pk是否在区域Hh(a,P,R)(1≤h≤q,a∈P,q为区域的数量)中的两个依据为:①在多维空间中,确认Pk是在参考点R的“下方”,即R的各维数据均大于Pk,使得Pk被参考点R支配;②确认点Pk支配的云服务点的集合Y不是空集。如果两个条件满足,则点Pk在区域Hh(a,P,R)中,有h=|Y|,且a∈Y,说明a在第h部分区域。如图2所示,H2(a,P,R)两块区域中的点分别支配集合Y=(a,c)和Y′=(a,b)的云服务点,故h=|Y|=2。如果上面两个条件有一个不满足,则Pk不在区域Hh(a,P,R)中。

定义2用于统计h区域中采样点的数量。
通过上面的定义及说明,计算对应部分的体积估计值:
(5)
由大数定理可知,适当增加n可以逼近对应超体积的真实值。因为多个不同的云服务点和共同的参考点分别围成的区域间可能重叠,所以设置共享权重系数
(6)
则a对应的蒙特卡洛估计超体积值
(7)

由于虚假云服务的特点,采用蒙特卡洛估计超体积法计算得到的这类云服务评价指标蒙特卡洛估计超体积值较大,通过设定超体积最低标准值,判别云服务是否为虚假或恶意云服务。
由超体积算法以及设定的最低标准值云服务点可知,任意云服务与最低标准值云服务点(以下称为标准点)存在3种关系:
(1)支配标准点 这类云服务的各维数值大于标准点,其超体积值小于标准点的超体积值,这类云服务被认定为非虚假或非恶意的云服务,可以全部保留。
(2)被标准点支配 这类云服务的各维数值小于标准点数值,认定为虚假云服务点,其超体积值大于标准点的超体积值,这类云服务能够完全剔除。
(3)与标准点互不支配 这类差异性表现在云服务某些维度的属性值小于标准点数值,甚至极小,根据超体积算法综合考虑各个维度,剔除其中超体积值大于标准点超体积值的云服务,即将这类云服务认定为虚假云服务。
超体积算法处理这部分云服务时,可能会保留一些质量不好的云服务,但是通过后续的聚类算法能够保证不将这类虚假云服务推荐给用户。
3 基于遗传算法的模糊c均值聚类算法对云服务的可信度评估
为了给用户推荐优秀的云服务或云服务集合,并使被推荐的云服务各维数值相差不悬殊,本文综合考虑各维度属性,利用聚类算法评价云服务的可信度等级,该方法能够明确两个不同集合云服务的差异,并保证不选择未能识别的虚假云服务,而且后续操作只需考虑优秀的云服务集合,从而减少数据处理量。
分析现有文献可知,本文将模糊聚类应用于云服务可信度评估,能够通过改进的模糊聚类方法划分云服务可信度等级,将可信度等级最高的云服务聚类集推荐给云用户。本文采用聚类算法将所有云服务归为A(好),B(良好),C(较好),D(一般),E(差)5个可信度等级集合。
3.1 模糊c均值聚类算法
定义3P={P1,P2,…,Pk,…,Pn}⊆ΩM是制造云服务空间ΩM中的一个有限数据集合,M为云服务评价指标的维数,n为云服务的个数,则对P的c(2≤c≤n)个模糊聚类划分是一个c×n矩阵U=(uik)cn∈Ωc×n,模糊分类矩阵U满足如下条件:
0≤uik≤1,1≤i≤c,1≤k≤n;
式中uik为第k个云服务属于第i类的隶属度值。
基于上述定义,FCM描述为求(U,V)使下式最小化:
(8)
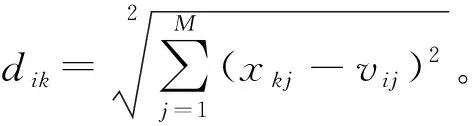
式(8)是一个关于(U,V)的约束优化问题,利用极值点的K-T(Kuhn-Tucker)必要条件,得到如下迭代公式:
i=1,2,…,c,k=1,2,…,n。
(9)
i=1,2,…,c,j=1,2,…,M。
(10)
FCM流程为:①设定聚类个数c和模糊系数m,初始化聚类中心V0和收敛精度ε,令迭代次数t=1;②用式(9)计算Ut+1;③用式(10)计算Vt+1,令t=t+1;④若‖Vt+1-Vt‖<ε或达到最大迭代数tmax,则输出Vt+1,否则返回步骤②继续迭代。
3.2 面向云服务可信度评估的基于遗传算法的模糊c均值聚类算法
由于FCM在聚类过程中容易因初始值不佳陷入局部收敛点,有学者将FCM与不同群体智能算法结合[14-16]。如果与GA结合,则可将GA算法的染色体设置为隶属度矩阵或聚类中心,染色体若为隶属度矩阵,则迭代搜索和寻优性能较低,不能满足算法需要。本文提出面向云服务可信度评估的基于GA的FCM采用聚类中心为GA的染色体。
3.2.1 初始聚类中心的选取
设聚类数为c,初始聚类中心V0=[v1,v2,…,vi,…,vc]T,有vi=[vi1,vi2,…,vij,…,viM],则
vij=rand×(max(zij)-min(zij))。
(11)
式中:rand∈(0,1);max(zij)和min(zij)分别为n个云服务中第j维数据的最大值和最小值。
3.2.2 算法步骤
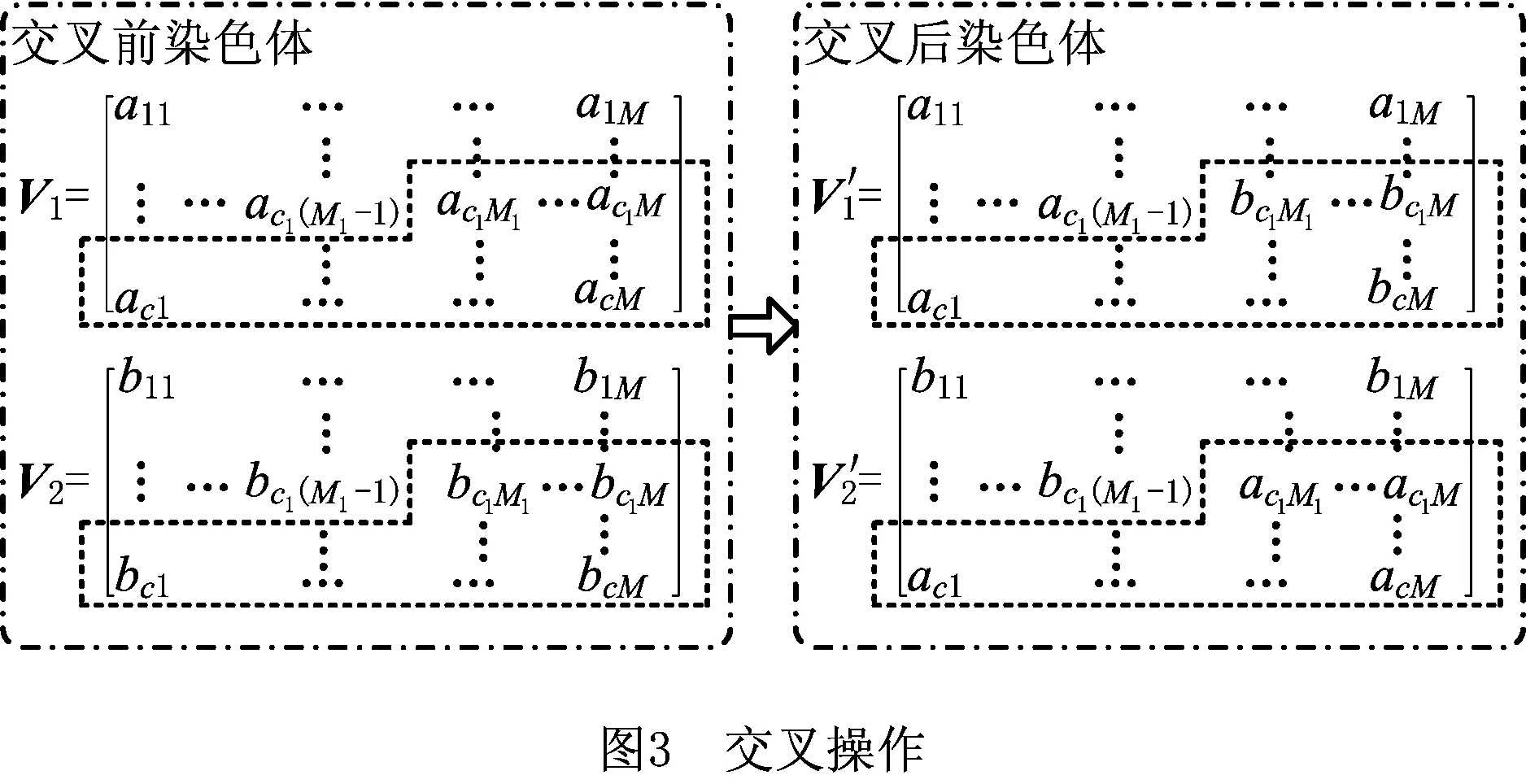
面向云服务可信度评估的基于GA的FCM操作包括编码、生成初始群体、选择、交叉、变异。
(1)编码 基于制造云服务的数据集特点,本文采用元胞数组对聚类中心进行编码,每个染色体,即每个元胞对应一个聚类中心,为c×M矩阵,染色体V=(vij)cM∈Rc×M。
(2)生成初始群体 利用式(11)生成Num个初始聚类中心V0,即为初始群体Po。
(3)选择操作 计算当代群体中每一个个体(聚类中心)的适应度,按适应度大小用轮盘选择法选择用于交叉的父本。
将每个分类集到各自聚类中心的欧式距离之和最小化作为聚类准则,建立适应度函数
(12)
i=1,2,…,c,j=1,2,…,M。
(13)
基于以上方法,面向云服务可信度评估的基于GA的FCM的步骤为:
(1)设置参数模糊指数m、模糊聚类数c、种群规模Num、外部档案个数Enum、交叉概率Pc、变异概率Pm、最大迭代次数tmax。
(2)获取初始聚类中心,得到初始聚类中心种群Po,t=0。
(3)用式(12)计算适应度值,为保留父代个体的优越性,建立外部档案,选取适应度值大的个体放入外部档案。
(4)基于FCM计算模糊分类矩阵U,更新聚类中心种群为Po′。
(5)利用遗传算子对Po′进行选择、交叉、变异操作,得到种群Po″。
(6)计算3个种群Po,Po′,Po″中个体的适应度值,更新外部档案。
(7)判断是否满足终止条件,不满足则t=t+1,返回(4);满足则输出外部档案中适应值最小的基因为聚类中心Vt。
3.3 云服务可信度评估等级判定
对3.2节得到的云服务聚类中心Vt,按照下式判断可信度评价等级:
(14)
式中VGi表示第i个聚类中心M维数据值的乘积,按乘积大小决定可信度等级,乘积越大,可信度等级越高,分级按照A,B等依次类推。
3.4 聚类算法验证
为了验证算法的有效性,同时考虑聚类效果的可视性,实验选择对5项评价指标进行主成分分析,确定用于测试的3项指标。对第1章云服务信息中5项评价指标(性能描述、参数配置、实物图或视频、供应商、询价评分)中的3项开展测试,结果如表1所示。从表1中选取方差百分比大的3个指标值,即性能描述、云服务参数配置、服务提供者的实物操作图或视频描述,用本章聚类算法对云服务进行聚类。
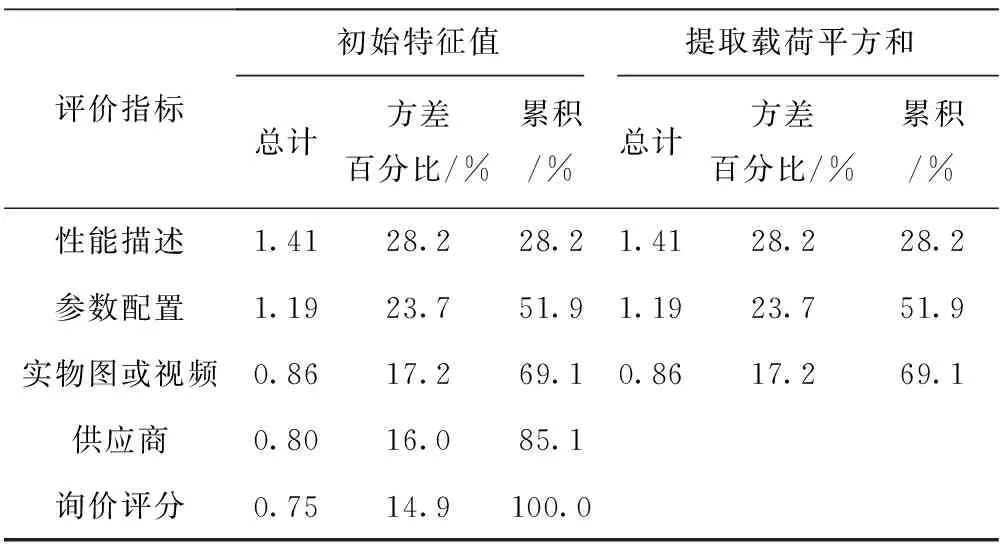
表1 主成分分析总方差
聚类算法参数为:模糊指数m=2,模糊聚类数c=5,种群规模Num=50,外部档案个数Enum=10,交叉概率Pc=0.8,变异概率Pm=0.2,最大迭代次数tmax=150。聚类结果如图4所示。图中3个坐标为主成分分析后选定的3个指标,x1轴代表性能描述,x2轴代表参数配置,x3轴代表实物图或视频供应。
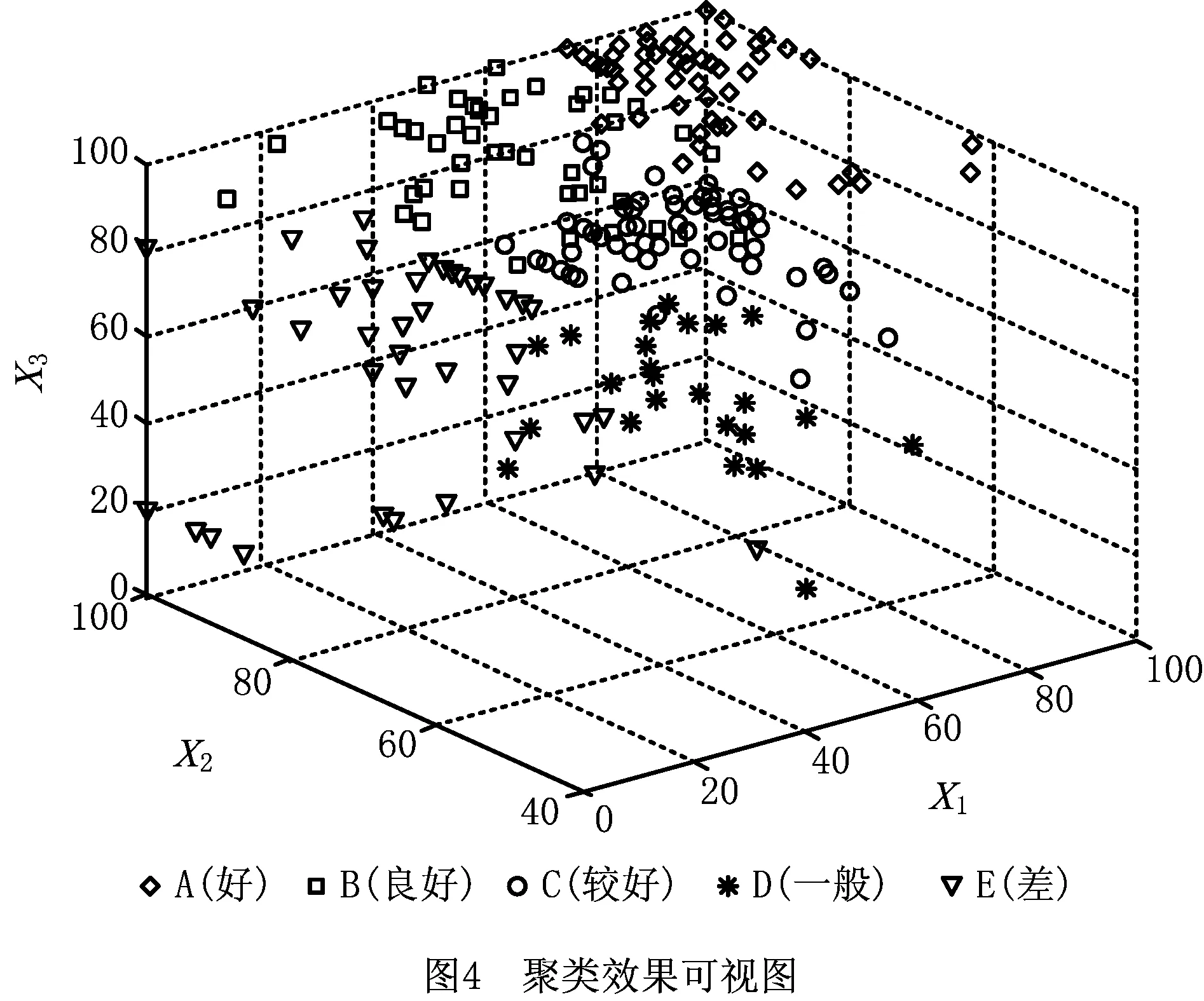
从图中看出基于GA的FCM精准地将云服务集分为5个聚类,A类云服务聚类明显,B与A或C类的交界处存在一些模糊状态,分界线不明显,一些点在聚类时出现偏差。总体上,面向云服务可信度评估的基于GA的FCM对云服务的聚类比较理想,满足实验要求。
4 制造云服务组合赋权综合评价
由于各指标对云服务质量的影响程度不同,从主观和客观的角度考虑,在“好”、“良好”集合中选择云服务进行评价,并按照评价分数从高到低优先推荐给使用者参考,从而确保与标准点互不支配的未被剔除的虚假云服务点不被选择。建立如图1所示的指标层次分析结构,通过层次分析法和熵值法分别计算指标权重和组合权重,然后进行综合评价,得到各云服务的评价值。
为克服AHP层次分析法主观性较强、不依赖数据,熵值法数据之间缺少横向比较、过于依赖数据的缺点,本文将两种方法结合,形成组合赋权评价法。按照层次分析结构,对云服务评价指标构造一级指标层判断矩阵F和二级指标层判断矩阵GF1,GF2,GF3,完成矩阵一致性检验(计算矩阵最大特征值λmax、一致性指标CI、一致性比率CR)、层次单排序和层次总排序,确定每项指标的权重αj,即主观权重。AHP法的详细流程请参见文献[17]。熵值法中,经过5个步骤计算云服务二级指标层的5项指标,即构造判断矩阵,进行归一化处理,计算每项指标熵值ej、指标差异系数εj和每项指标熵值权重βj(即客观权重)。具体流程请参考文献[18],AHP法与熵值法的综合评价流程请参考文献[19-23]。
上述两种评估方法不同,得到的权重也不同,为了避免两个权重之间差异较大,对所得权重进行一致性检验,公式为
(15)
式中d(αβ)为距离,表示两种方法确定权重的一致性程度,当0≤d(αβ)≤1时,赋权结果通过一致性检验。
对一致性检验后的权重进行组合赋权,步骤如下:
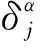
j=1,2,…,M。
(16)
(2)为使得到的两权重差异最小,以组合赋权法的权重与主客观权重之间的误差平方和最小为目标:
(17)
wj=0.5αj+0.5βj。
(18)
(4)采用式(18)得到每个云服务的组合赋权权重,以此计算某个制造云服务的综合评价值
(19)
5 基于可信度和综合评价的制造云服务优选
基于可信度和组合赋权综合评价值的制造云服务优选过程如下,优选过程中设定可信度评价等级的优先级别高于综合评价值:
(1)当云服务评价等级相同时,根据综合评价值VCS的高低进行优选。
(2)当云服务评价等级不同时分为两类:①云服务i的评价等级优于云服务j,且VCS,高于云服务j,则选择云服务i;②云服务i的评价等级优于云服务j,但VCS低于云服务j,若评价等级相邻,且VCS在允许误差δ(δ<10)范围内,则选择云服务i,否则选择云服务j;若评价等级相差至少两个级别,则优先选择可信度级别高的云服务。
6 实验分析
某用户采购中大型挖掘机,希望推荐10个云服务优选方案。通过网页爬虫技术获取“铁臂商城”平台上300个挖掘机云服务,爬取包括ID在内的3 000条云服务信息,对得到的数据进行量化处理。
6.1 虚假云服务识别
设超体积参考点R=[101,101,101,101,101],每一云服务的评价指标都对应一个超体积值,设定最低标准值,计算最低标准值对应的超体积值,作为超体积大小的衡量标准。如果云服务超体积大于最低标准值对应的超体积差值,则判定该云服务为虚假云服务,反之判定为真。
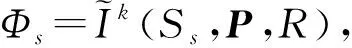

表2 虚假云服务剔除结果
6.2 可信度评估
利用基于GA的FCM对剔除虚假云服务后含260个云服务数据的数据集进行可信度等级评估,算法参数与3.4节一致。经算法优化后,可信度聚类中心为

上述矩阵从上到下分别对应云服务可信度的5个等级A,B,C,D,E,如表3所示。
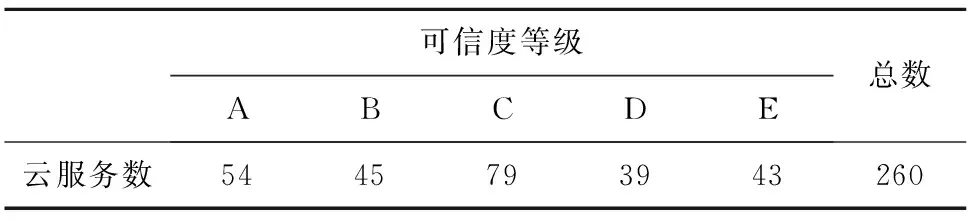
表3 可信度等级分类统计表
6.3 组合赋权综合评价
建立一级指标判断矩阵及权重如表4所示。
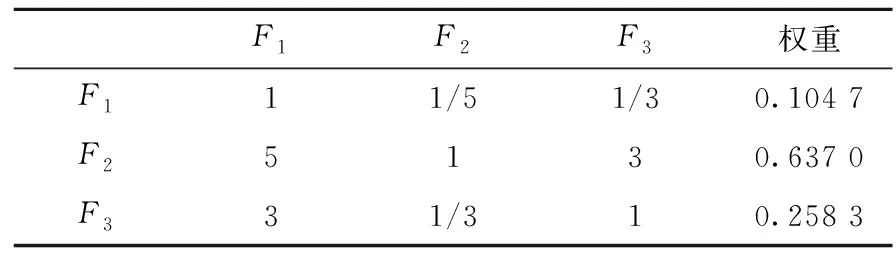
表4 一级指标判段矩阵及权重
由表可得λmax=3.038 5,一致性指标CI=0.019 3,随机一致性指标RI=0.58,一致性比率CR=0.033 2<0.1,判断矩阵符合一致性要求。
建立二级指标判断矩阵及权重,如表5~表7所示。
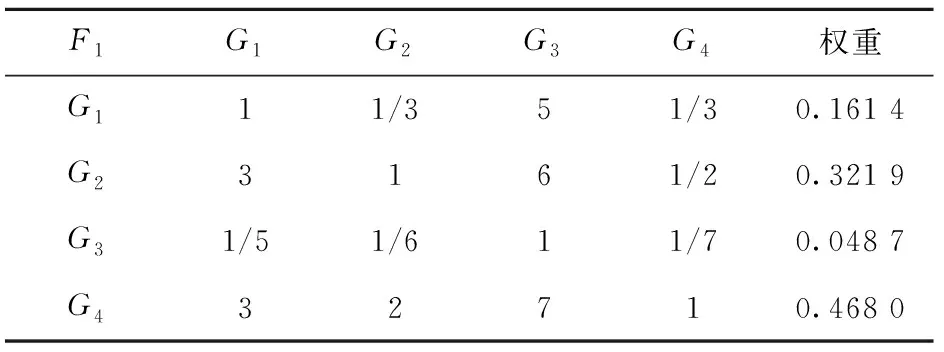
表5 服务完备性的二级指标判段矩阵及权重
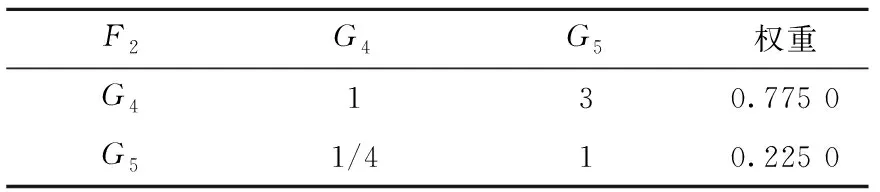
表6 可靠性的二级指标判段矩阵及权重
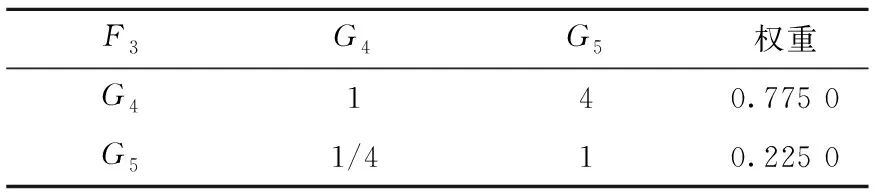
表7 交互性的二级指标判段矩阵及权重
由表可得λmax=4.138 7,CI=0.046 2,RI=0.90,CR=0.051 4<0.1,判断矩阵符合一致性要求,是满意一致性矩阵。
由表可得λmax=1.866 0,因为判断矩阵为二阶矩阵,RI=0,所以判断矩阵符合一致性要求,是满意一致性矩阵。因为表7数据与表6相同,所以也是满意一致性矩阵。
通过层次总排序得AHP法各指标的总权重,如表8所示。
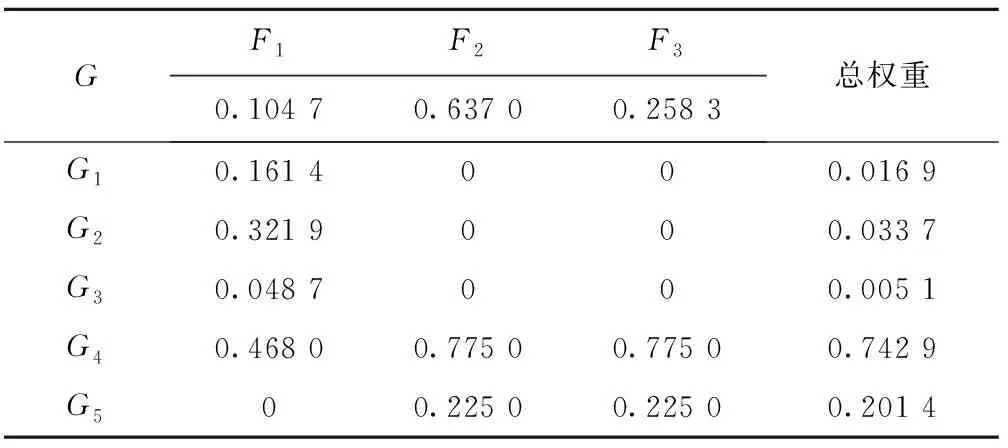
表8 AHP法各指标的总权重
利用熵值法求得5项指标的熵权重,如表9所示。

表9 每项指标熵值权重
采用式(15)对AHP法和熵值法得到的权重进行一致性检验,得d(uv)=0.551 4<1,权重通过一致性检验。
由式(19)得各指标的组合权重,如表10所示。

表10 每项指标的组合权重
6.4 方案优选
由于可信度等级为A的云服务有54个,不需要对其他等级云服务进行赋权综合评价,将A集合中的云服务推荐给用户,对挖掘机云服务进行组合赋权综合评价,根据评价指标选取综合评价值前10个云服务作为用户的优先参考,其各项指标如表11所示,基于可信度和综合评价的结果如表12所示。
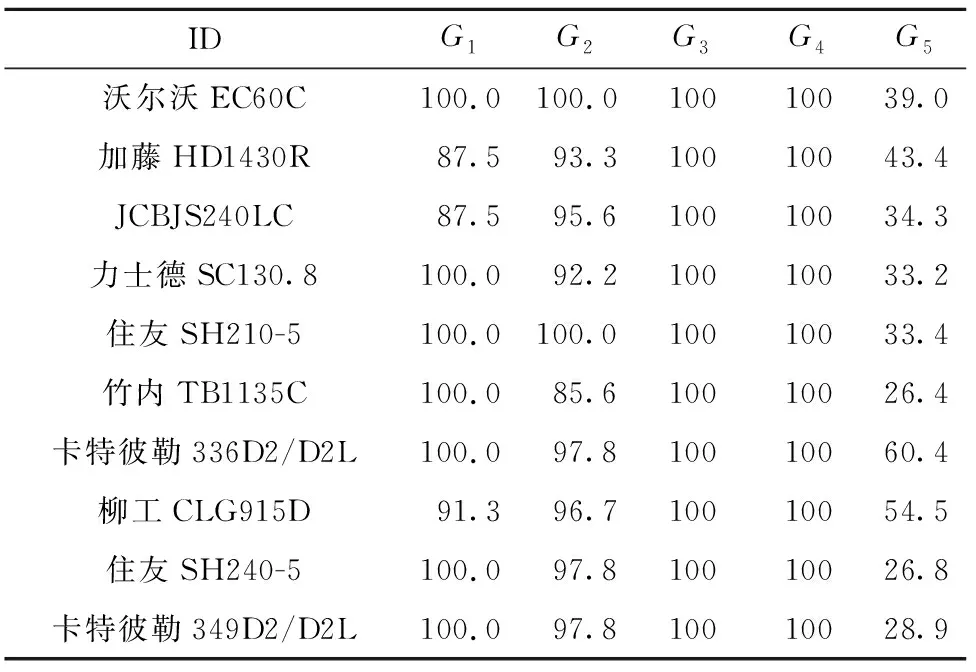
表11 选取的10个云服务指标

表12 实验结果
按照第5章给出的基于可信度和综合评价值的组合制造云服务优选方案确定本实验推荐的优秀云服务集合A,提供给用户参考的优先级较高的云服务按照挖掘机ID排序依次为ID7-ID8-ID1-ID5-ID4-ID2-ID10-ID9-ID3-ID6。
7 结束语
云制造服务模式的提出为全球制造业服务模式转型奠定了坚实的基础,而且这种新的制造服务模式对改善我国制造业发展现状、促进制造业服务水平升级具有积极作用,可以很好地满足我国目前制造业发展市场的需求。制造云服务的虚假识别和云服务推荐优选研究是云制造服务模式发展中的关键技术之一,本文提出一种基于超体积的算法来识别和剔除虚假云服务,并根据可信度等级结合综合评价值建立云服务优化评估算法,对云服务进行优选。所提算法实现了虚假制造云服务识别和云服务最优选择,通过实例也验证了算法具有有效性和优越性。
