基于平面光栅的机床几何误差测量与辨识

郭世杰，梅雪松，姜歌东+

(1.内蒙古工业大学 机械工程学院，内蒙古 呼和浩特 010051；2.西安交通大学 机械工程学院，陕西 西安 710049)

0 引言

几何精度是评价机床性能的重要参数[1-2]，几何误差是机床几何精度的直接体现，也是决定机床加工精度的重要误差源[3-5]，通过实施误差补偿技术可以有效保证和提升机床的几何精度[6]。误差补偿技术包括误差建模、误差测量及辨识、误差补偿，其中误差测量及辨识是误差预测的关键，是开展误差补偿的前提[7]。因此，几何误差辨识值的准确性决定了预测结果的优劣，实施高效、准确地辨识对提升机床精度具有重要作用。

国内外众多研究院所针对几何误差测量及辨识方法进行了广泛研究，并提出诸多有效方案[8-11]。根据几何误差辨识方法的差异性，几何误差测量分为以测量仪器为核心的直接测量辨识法和以测量策略为核心的间接测量辨识方法[12-13]。在直接测量法中，最为常用的是激光干涉仪和跟踪仪。韩飞飞等[14]基于雷尼绍XL-80型激光干涉仪直接测量并辨识了直线轴定位误差、直线度误差和角度误差，并分析了直线轴定位误差与相应轴向误差向量间的关联性；Cheng等[15]利用API-6D激光干涉仪经多次测量量化了四轴卧式镗床的空间几何误差分布特征；Ibaraki等[16]利用激光跟踪仪测量了机床工作空间内测点3个方向的误差向量，通过最小二乘法确定了几何误差的数值。目前，API-6D型激光干涉仪和Renishaw XM-60型激光干涉仪可实现一次安装测量并辨识6项几何误差，但前者需配备电子水平仪直接测量滚转角，后者成本较高且光路校准繁琐，测量结果易受周围环境影响[1]，因此API-6D和Renishaw XM-60型6自由度几何误差测量系统未被ISO 230系列标准[17]推荐。激光干涉、跟踪仪和球杆仪(Double Ball Bar，DBB)是间接测量方法常用的测量仪器，间接测量法利用规划的空间测量轨迹和所建立的综合误差模型进行几何误差解耦辨识。Li等[18]在九线法和十二线法[19]的基础上提出十三线法，并对三轴机床的21项几何误差进行了辨识；He等[20]提出双路激光测量方法，利用激光干涉仪测量空间轨迹的几何关系辨识了直线轴滚转误差以外的其他几何误差项；田文杰等[21]利用DBB测量了空间共球面三圆弧轨迹，并利用岭回归方法辨识了直线轴的全部几何误差，通过与最小二乘法的拟合结果对比验证了所提测量方案的可行性；Lee等[22]利用DBB对五轴机床旋转轴连接误差和运动误差进行了同步辨识；Guo等[23]利用DBB在4个位置测量圆轨迹，辨识了五轴机床旋转轴的全部连接误差。ISO 230-1[17]标准推荐采用基于激光干涉仪测量的空间体对角线测量方法和激光干涉仪测量的分步体对角线测量方法，然而体对角线检测方法假设角度误差较小，而且测量结果仅能作为机床精度的评价手段，不能测量误差项的精准值；分步对角线法因为测量路径多，所以在测量过程中会耦合动态误差。DBB和跟踪仪的综合精度为1 μm～101μm，达不到亚微米，针对这一不足，Knapp等[24]设计了精度为纳米级的平面光栅测量系统，即GGE(gross grid encoder)，该系统同时具备激光干涉仪和DBB的功能，可以测量机床工作空间内任一平面上的复杂轨迹；Du等[25]利用Haidenhaim平面光栅在三轴机床上测量圆轨迹、直线轨迹和折线轨迹，提出8种角度误差辨识方案，并辨识出三轴机床的21项几何误差值。对高精密机床而言，ISO有使用GGE测量圆轨迹来评价机床精度的规定，但对利用其设计何种方式的测量轨迹来辨识几何误差数值的研究尚停留在探索阶段，现有的利用GGE检测机床几何精度的方法较少[1,26]，已有测量方法由于测量路径为复合轨迹，测量过程存在间断性，容易受安装误差的影响。因此，如何利用测量读数精度可达纳米级的GGE高效准确地测量和辨识数控机床几何误差是当前机床研究领域的热点。

为了完善现有研究方法，本文在已有研究基础上提出一种基于平面光栅的面—线测量和辨识新方法。通过3次安装，在3个相互垂直的平面内分别通过测量一次直线轨迹来规划路径，减少由于安装在特定位置而产生的安装误差累积效应，并统一各测量平面的测量基准点与误差原点之间的位置关系。根据多体系统理论建立综合几何误差模型，依次辨识垂直度误差、俯仰误差、偏摆误差、定位误差、直线度误差和滚转误差在内的21项几何误差值。最后采用基于激光干涉仪的九线法进行几何误差测量和辨识，对比验证本文方法的有效性。

1 数控机床几何误差建模

1.1 几何误差的定义

根据刚体假设，空间中的物体有6个自由度。实际状态下刚体在相应的自由度上存在与理想状态偏离的代数值(偏差值)，对数控机床而言，该偏差值源于零部件在制造和装配过程存在的缺陷和不精确问题，最终形成几何误差。以Y直线轴为例，其6项几何误差如图1所示。

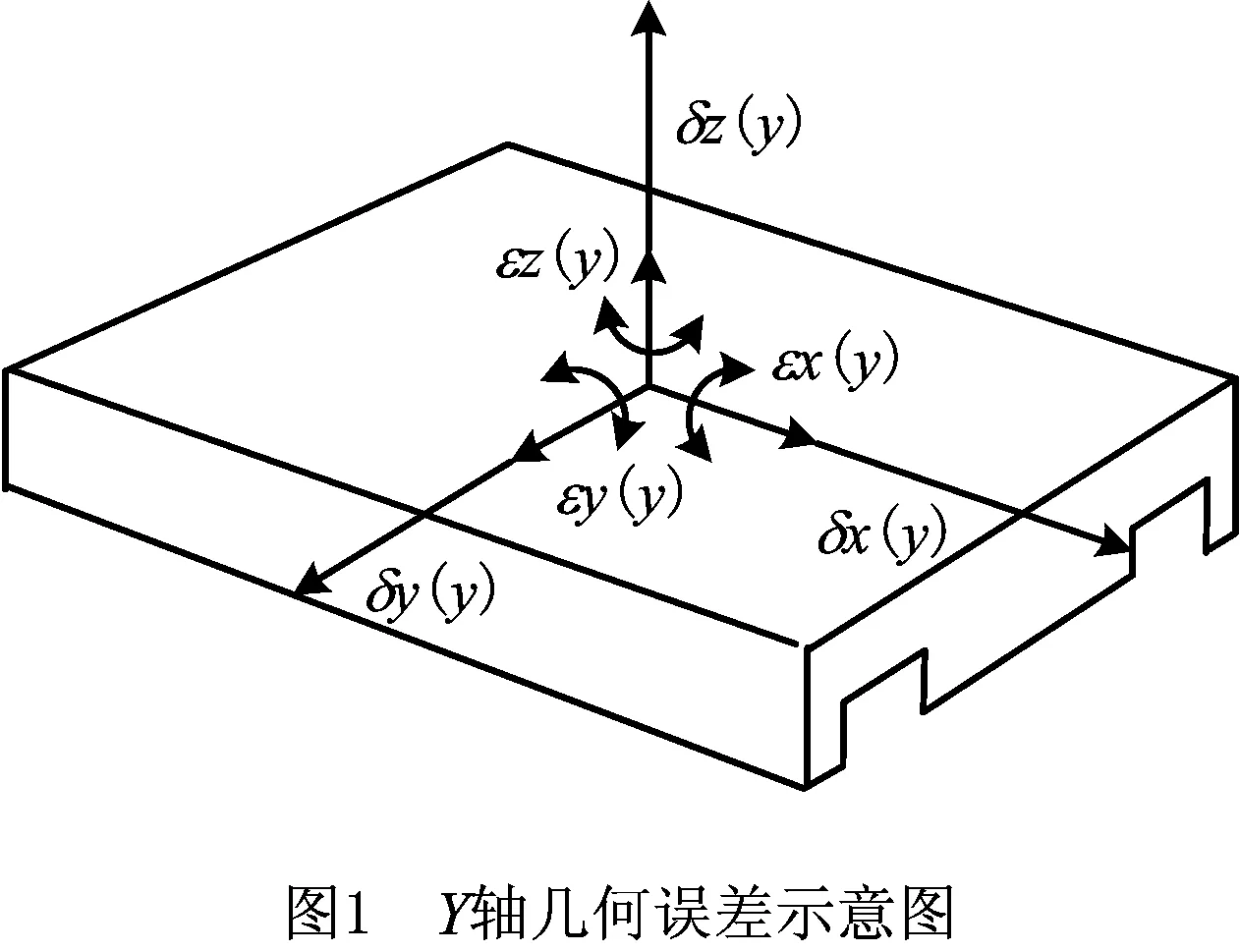
Y直线轴包括3项线性误差(δx(y)，δy(y)，δz(y))和3项角度误差(εx(y)，εy(y)，εz(y))。图1的误差元素δi(j)，εk(j)中，δ表示定位误差和直线度误差，ε表示滚转误差、俯仰误差和偏摆误差，i表示误差所在的方向，k表示角度误差所绕的方向，j表示运动的直线轴。另外，3个直线轴之间的3项角度误差即垂直度误差Slm，S表示垂直度误差，l，m表示两个直线轴。三轴机床的21项几何误差如表1所示。

表1 机床几何误差的定义

1.2 机床结构及坐标系的建立

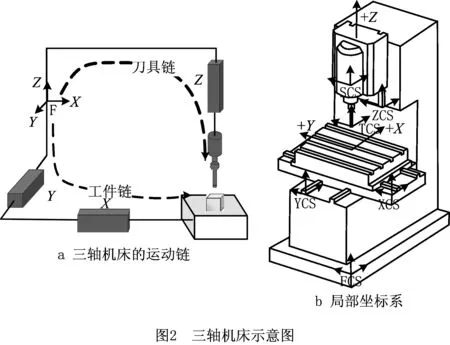
根据多体系统理论，三轴数控机床可视为由刀具链和工件链组成的多体系统，如图2a所示。三轴数控机床的运动部件主要包括X，Y，Z轴导轨、工作台、主轴、刀具等，X，Y，Z三轴联动可完成空间范围内的运动，其利用刀具和工件之间的相对运动进行切削加工。

将机床抽象成多个部件，每个部件看作一个刚体，图2a中的三轴机床属于XYFZ型，F表示机床床身，其左边的字母表示工件链(工件相对于床身移动)，右边的字母表示刀具链(刀具相对于床身移动)。在机床床身上建立机床坐标系FCS(foundation coordinate system)，以及固结于X，Y，Z轴上的局部坐标系XCS(X-axis coordinate system)，YCS(Y-axis coordinate system)，ZCS(Z-axis coordinate system)，各局部坐标系的方向与机床坐标系的方向相同(如图2b)，工件坐标系WCS (workpiece coordinate system)、主轴坐标系SCS(spindle coordinate system)和刀具坐标系TCS(tool coordinate system)分别与工作台、Z轴和主轴连接。

1.3 机床几何误差建模

三轴数控机床可视为典型的多体系统，由各局部坐标系之间的位置关系可知WCS与XCS、SCS与ZCS、TCS与SCS之间的位置变换关系可用单位矩阵表征[27-28]。刀具安装于机床的主轴上，主轴端的安装制造精度较高，工件通过专用夹具安装于工作台端，利用约束限制其自由度，可忽略主轴、刀具及被加工件几何误差的影响。理想状态下，机床各个部件在X，Y，Z轴驱动下沿正向运动x，y，z距离时，相邻两部件之间的位置变化关系表示为：

(1)

在此状态下，工件切削接触点与刀尖切削点完全重合，工件链上各局部坐标经齐次变换传递至机床坐标系的位置与刀具链经坐标变换传递至机床坐标系的位置相同，即：

(2)

(3)

(4)

机床在实际运行过程中需要考虑各项几何误差对运动部件位姿的作用，即各位置误差和角度误差对位置变换矩阵产生的影响。当工作台沿Y轴导轨运动距离y时，用齐次坐标变换表达6项几何误差，忽略高阶误差项，可得由YCS到FCS的变换矩阵为

(5)

同理，当工作台沿X，Z轴导轨分别运动x，z时，X轴的6项几何误差和垂直度误差Sxy影响X轴的位姿，Z轴的6项几何误差和垂直度误差Sxz，Syz影响Z轴的位姿，利用空间齐次坐标变换表达上述几何误差项，忽略高阶误差项，基于小角度假设可定义角度误差的正弦函数等于其本身，余弦函数等于1，从而得到由XCS到YCS的变换矩阵(式(6))和由ZCS到FCS的变换矩阵(式(7))：

(7)

在实际状态下，工件链末端的被加工件切削点与刀具链末端的刀具接触点并不重合，即存在相对位置偏差，此时有:

(8)

(9)

(10)

由理想状态和实际状态下工件切削点和刀尖点的位姿关系，将上述几何误差的齐次矩阵带入式(10)可知

(11)

化简后得到如图2所示的XYFZ型三轴立式数控机床的空间几何误差模型为:

(12)

利用式(12)可进行几何误差辨识和几何误差预测，与常规几何误差模型相比[28-29]，式(12)所表达的误差模型包括了XYFZ类型三轴数控机床的全部几何误差(21项)。将刀尖点和工件的被切削点按刀具链、工件链分别变换至机床床身参考坐标系，能够统一几何误差的表达基准，使误差测量和误差辨识更灵活。

2 基于平面光栅的测量及辨识方案

面—线法利用平面光栅测量设定轨迹的坐标值，分别在三轴数控机床的运动平面XOY(平面Ⅰ)，XOZ(平面Ⅱ)，YOZ(平面Ⅲ)上根据预定轨迹进行测量，然后根据顺序采用相应的辨识方法分别辨识耦合的几何误差值，仅需在3个平面分别连续测量5条线段即可快速辨识得到三轴数控机床的全部空间几何误差项。

2.1 测量方案及路径规划

设置YOZ，XOZ水平测量方向的边界靠近测量坐标系的Z轴，XOY面的起始测量点设在区域的原点。当利用L10和L12辨识X轴的定位误差时，先进行角度误差辨识，再使用其与L10的数据进行分析，求得X轴上定位误差的值，此时因为AⅠ点的Y坐标不为0，所以Y轴的偏摆误差不为0，使Y坐标中耦合了Y轴偏摆误差，误差虽小但难以解耦。同理，在辨识Y轴定位误差时，也受到X轴角度误差的影响。因此，在辨识时将每个测量平面的基准点AⅠ通过几何关系统一至相同基准下。面—线法的测量轨迹如图3所示。

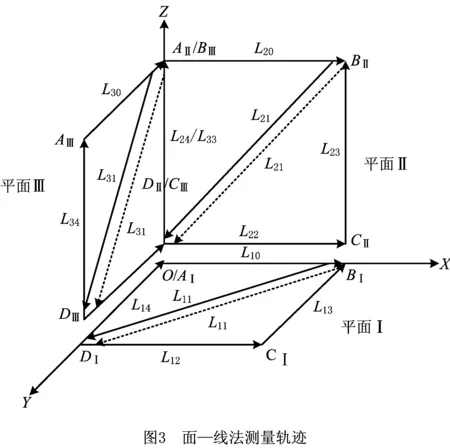
定义平面XOY，XOZ，YOZ分别为测量平面Ⅰ，Ⅱ，Ⅲ。针对测量平面Ⅰ，GGE测头的相对移动路径为AⅠ→BⅠ→DⅠ→CⅠ→BⅠ→DⅠ→AⅠ，所形成的测量路径如图3所示，其中虚线表示同一路径的第二次测量曲线，因此所记录数据不作为误差辨识的原始数据。同理，在测量平面Ⅱ和测量平面Ⅲ上划定相似的测量路径AⅡ→BⅡ→DⅡ→CⅡ→BⅡ→DⅡ→AⅡ和AⅢ→BⅢ→DⅢ→CⅢ→BⅢ→DⅢ→AⅢ。

2.2 几何误差辨识方法

测量过程中，以AⅠ点为基准点分析每个测量平面，辨识得到各项误差后，通过平面几何关系先将测量平面Ⅱ和测量平面Ⅲ的误差统一为以AⅡ点为基准，最后根据AⅡ点与O点的误差关系统一全部误差的基准。基于面—线法的测量辨识流程如图4所示。

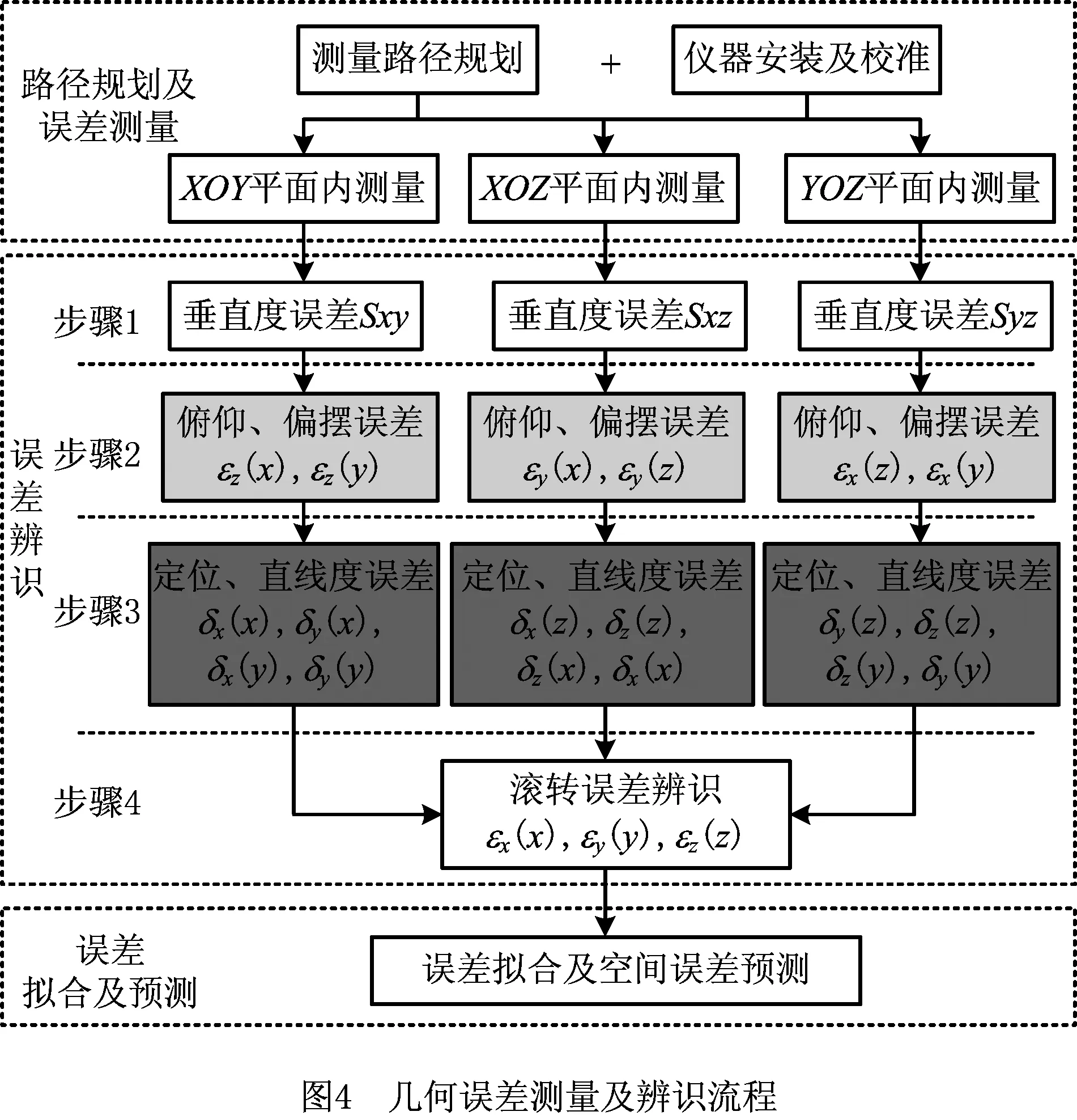
几何误差辨识步骤如下：

(1)垂直度误差测量及辨识

以测量平面Ⅰ为例，与平面Ⅰ有关的垂直度误差Sxy的几何关系如图5所示。

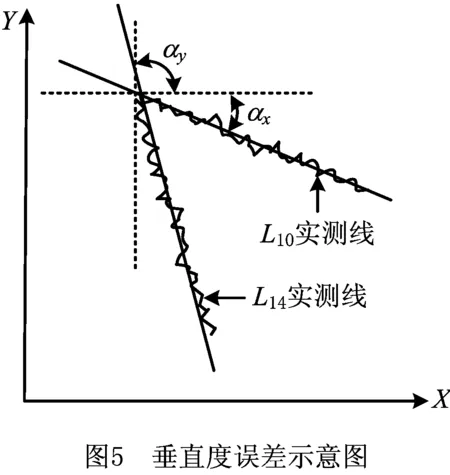
在图5中，以路径L10和路径L14为基准线，Sxy是以X轴为基准要素、以Y轴为被测要素的垂直度误差，实际测得的路径趋势线是与设定直线轨迹存在偏转角度的倾斜直线，根据多个测点的测值，采用最小二乘法拟合求出路径L10和L14的趋势线L0y=a0x+b0，L4x=a4x+b4，其中：

(13)

式中(xi,yi)为各测点的实际坐标值。

利用两条测量路径的趋势线斜率即可求出倾角αx,αy∈[0,π]，进而求出两轴间的垂直度误差为：

αx=tan-1a0,αy=tan-1a4；

(14)

(2)俯仰误差、偏摆误差的辨识

利用Sxy的辨识值，将路径L10和路径L12的趋势线旋转至平行X轴，消除耦合的垂直度误差影响，得到路径上修正的测点坐标为(xxl0,yxl0)，(xyl0,yyl0)；将路径L13和路径L14的趋势线旋转至平行Y轴，消除耦合的垂直度误差影响，得到路径上修正的测点坐标(xxl1,yxl1)，(xyl1,yyl1)。测量路径L10，L12，L13，L14上的测点理论值分别为(x1x,y10)，(x1x,y11)，(x11,y1y),(x10,y1y)，根据测点理论坐标值和修正坐标值确定路径L10上X轴测量范围内各测点的坐标偏差

Δx0=xxl0-x1x，

(15)

X轴测量范围内在Y方向的坐标偏差

Δy0=yxl0-y10。

(16)

在路径L14上采用相同方法得到Y轴测量范围内各测点的坐标偏差

Δy4=yxl0-y1y，

(17)

Y轴测量范围内在X方向的坐标偏差

Δx4=xyl0-x10。

(18)

路径L12上各测点的X坐标偏差值

Δx2=xxl1-xxl。

(19)

路径L13上各测点的Y坐标偏差值

Δy3=yyl1-yyl。

(20)

利用测量路径L12和路径L10上各测点处X的坐标偏差值，根据偏差值与几何误差之间的关系，可知X轴在XOY平面内的偏摆角度误差

(21)

根据测量路径L13和路径L14上各测点的X坐标偏差值，测量Y轴在XOY平面内的偏摆角度误差为

(22)

(3)定位误差、直线度误差辨识

消除角度误差对测量路径L10的影响以后，辨识得到X轴的定位误差δx(X)和Y向直线度误差δy(X)分别为：

δx(x)=Δx0+εzx·x10；

δy(x)=Δy0-εzx·y1x。

(23)

同理得到Y轴的定位误差δy(Y)和X向直线度误差δx(Y)分别为:

δx(y)=Δx4+εzy·y1y；

δy(y)=Δy4-εzy·x10。

(24)

类似地，对测量平面Ⅱ和测量平面Ⅲ进行轨迹测量，可辨识平面Ⅱ的垂直度误差Syz、俯仰角度误差与偏摆角度误差εx(z)，εx(y)，以及直线度和定位误差误差δy(y)，δz(y)，δz(z)，δy(z)。同理，可完成对平面Ⅲ内的角度误差εy(x)，εy(z)，以及直线度和定位误差δx(x)，δz(x)，δz(z)，δx(z)的辨识。

(4)滚转误差辨识

完成3个测量平面除滚转误差外的误差辨识后，结合已经建立的三轴机床空间几何误差模型式(12)，在3个测量平面上对各轴测量范围内存在重合段的公共区域进行滚转角度误差辨识。测量平面Ⅰ内误差模型中Δz=0时，可确定ΔxⅠ和ΔyⅠ与相关几何误差的函数关系为：

(25)

对于测量平面Ⅱ，误差模型中Δy=0时，可确定ΔxⅡ和ΔzⅡ与相关几何误差的函数关系为：

(26)

对于测量平面Ⅲ，误差模型中Δx=0，可确定ΔyⅢ和ΔzⅢ与相关几何误差的函数关系为：

(27)

利用式(25)～式(27)建立包括3项滚转几何误差的正定方程组，利用已经辨识出的定位误差、直线度误差、垂直度误差、俯仰偏摆角度误差和初始坐标值，可直接确定3个直线轴的滚转误差εx(x)，εy(y)，εz(z)。

3 实验验证

本文采用Haidenhaim KGM182光栅测量系统在配备华中8型的三轴数控机床上进行基于面—线法的几何误差测量实验。Haidenhaim KGM182光栅测量系统的参数指标如表2所示。

表2 GGE测量系统参数指标

该机床的X/Y/Z行程为850/560/650 mm，定位精度分别为0.016/0.012/0.012 mm，重复定位精度分别为0.008/0.006/0.005 mm；根据现行国际标准ISO 10791-2[30]和GB/T 20957.2-2007[31]的规定以及KGM182光栅测量系统的安装精度要求，GGE的安装过程中需采用千分表使平行度和垂直度分别小于0.01和0.015；通过调整扫描头与垫片间距，使读数头和光栅圆盘之间的间隙为0.5 mm。为保证3个平面内的平面光栅相互垂直，即3个平面内的平面光栅组成一个测量空间，3个测量平面内GGE的具体安装过程如下：

(1)当在XOY平面内测量时，使光栅的基准面平行于工作台的X轴方向，即利用千分表校准光栅和机床工作台的平行度，保证平行度误差小于0.01 mm，平面光栅与工作台间的垂直度由制造精度保证。

(2)当在YOZ平面内测量时，使光栅的基准面平行于工作台的Y轴方向，即利用千分表校准光栅和机床工作台的平行度，使其平行度误差小于0.01 mm。然后，利用专用工装的制造精度控制GGE沿Z轴方向的精度，并通过微调使垂直度小于0.015 mm。

(3)当在XOZ平面内测量时，需使用专用工装配合GGE的安装，使光栅的基准面平行于工作台的X轴方向，即利用千分表校准光栅和机床工作台的平行度，使其平行度误差小于0.01 mm。然后，利用专用工装的制造精度控制GGE沿Z轴方向的精度，并通过微调使垂直度小于0.015 mm。

为降低系统误差引起的测量不确定度对精度的影响，根据国际标准ISO 230-2[32]的规定连续进行5次测量，几何误差的辨识值为5次测量结果的均值。提高面—线法辨识精度的关键是对垂直度误差的准确辨识，为验证垂直度误差辨识结果的准确性，采用KGM182型平面正交圆光栅测量系统作为垂直度误差测量设备。以X轴为基准要素，Y轴为被测要素，测量范围内X轴和Y轴间的垂直度为被测要素与基准线之间的夹角，利用垂直于基准线之间的距离和测量范围有效值的比值可以补偿垂直度误差。测量半径R=50 mm，进给速度F=200 mm/min，测量整圆并记录误差值；利用数控系统的垂直度补偿功能，设补偿轴为X轴，基准轴为Y轴，将测量分析得到的垂直度误差值转换为角度值传入数控系统，并以测量原点为参考点进行X轴与Y轴间的垂直度误差补偿。补偿完成后，以相同的进给速度和测量半径在补偿前的测量位置再次对标准圆进行测试，获得XOY平面内以X轴为基准要素、Y轴为被测要素的垂直度。同理可确定Y轴和Z轴、X轴和Z轴间的垂直度误差。误差补偿前后，3个平面内测量辨识的误差测量曲线如图6～图8所示。

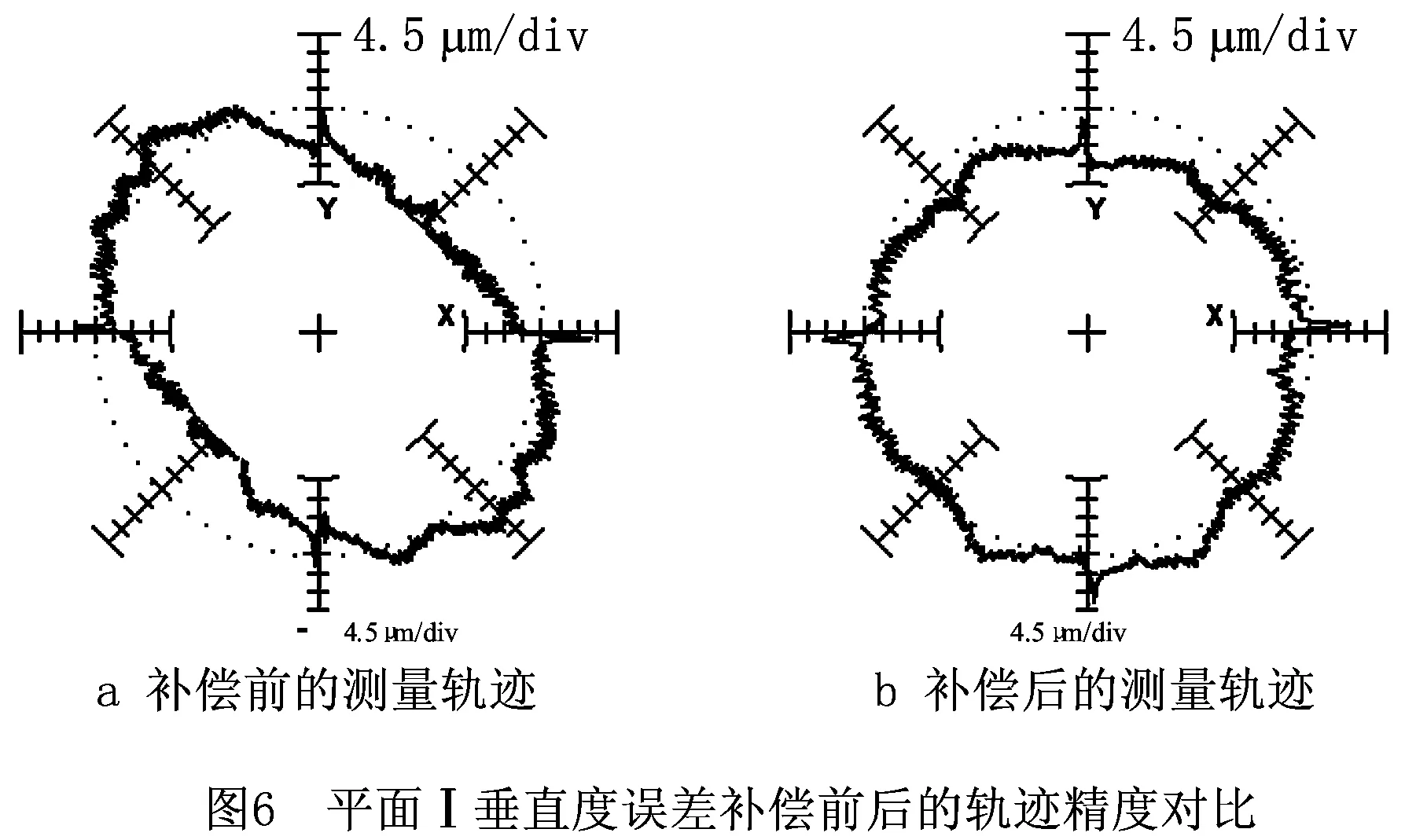
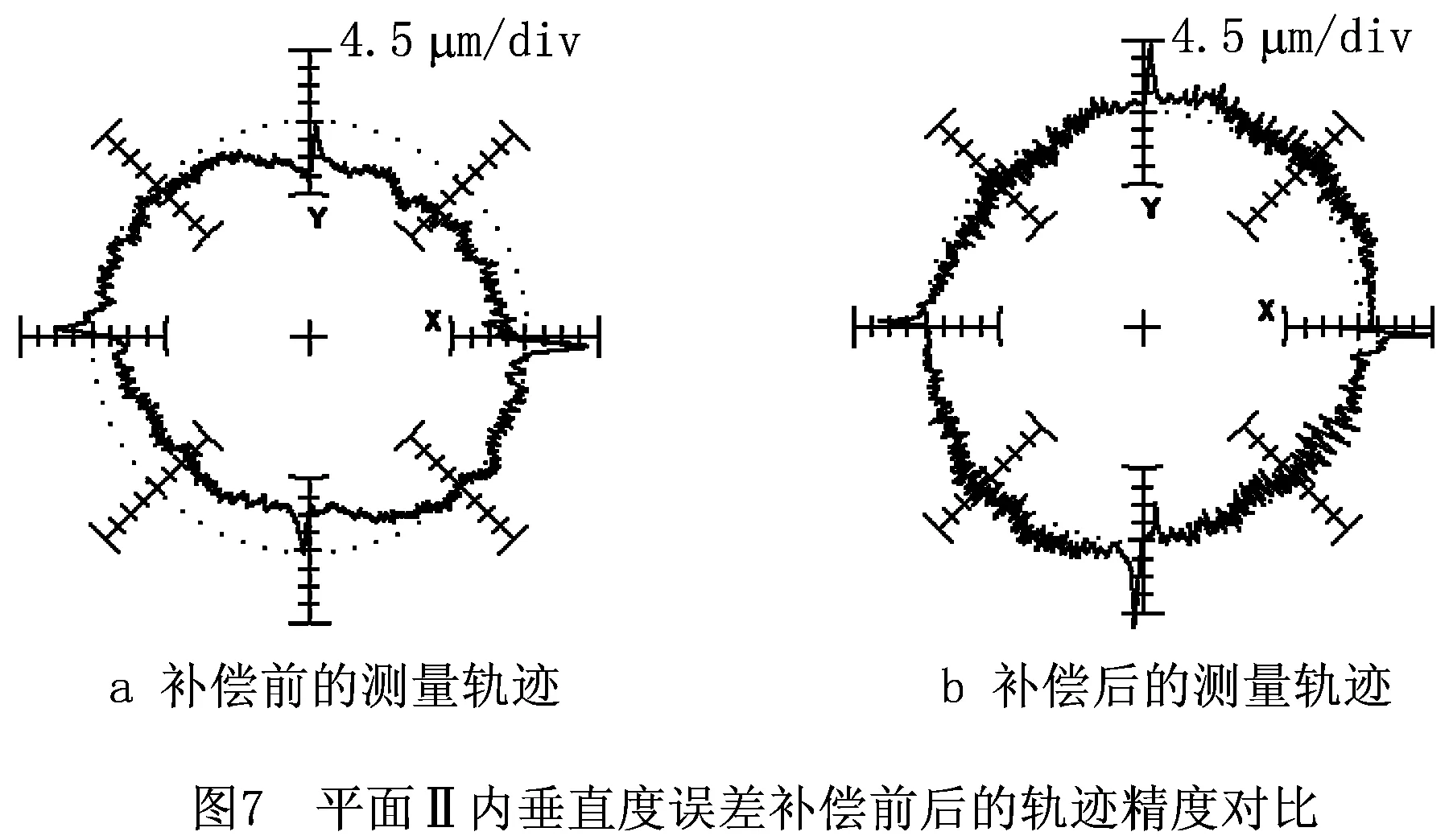
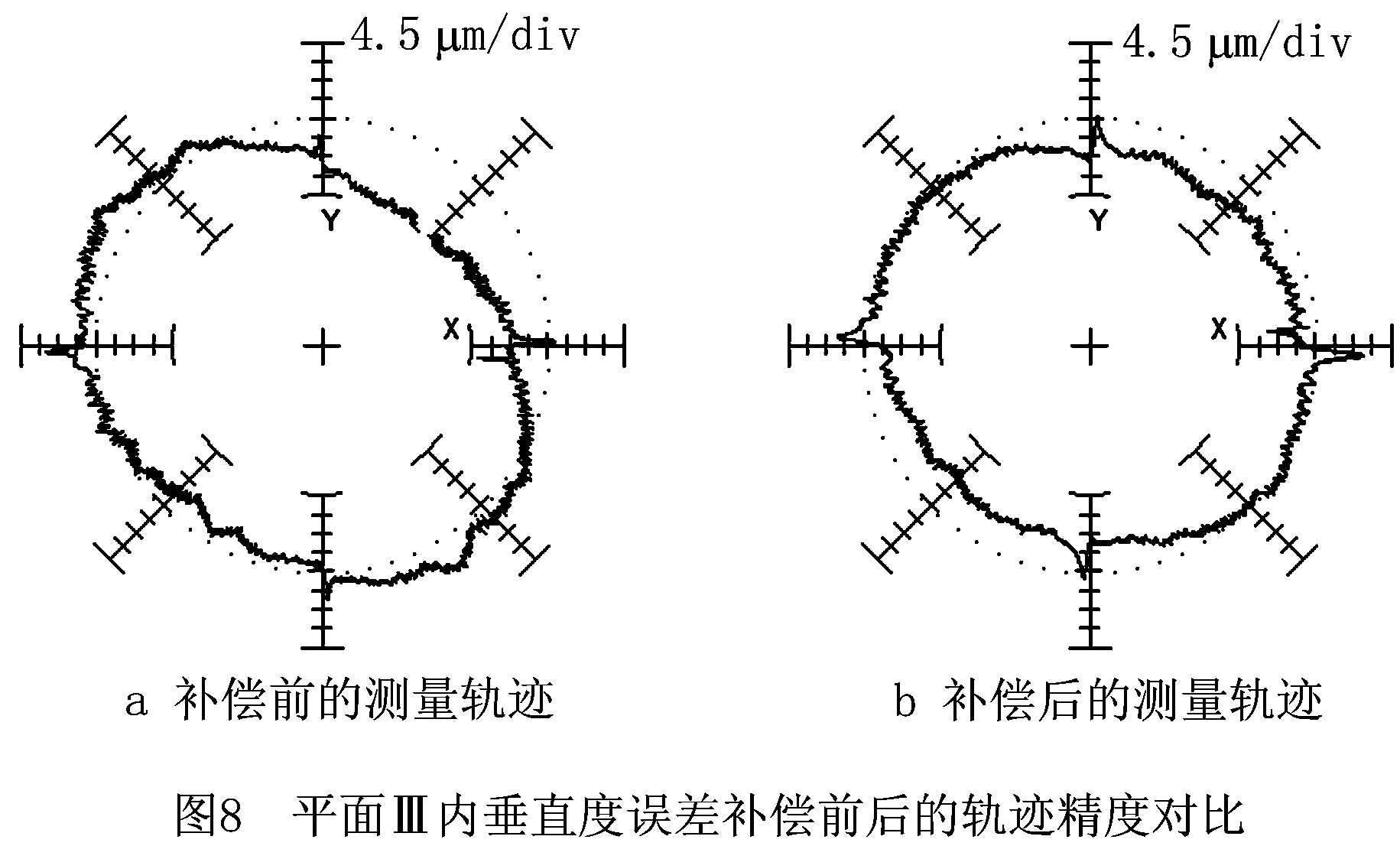
使用平面光栅配备的测量分析软件ACCOM对补偿前后测得的标准圆轨迹进行误差分析，补偿前分析得到X，Y两轴之间100 mm测量范围内的垂直度误差在补偿前为-271.538 5 μm/m，补偿后为-10.842 μm/m，垂直度误差降低96.1%；Y，Z两轴之间100 mm测量范围内的垂直度误差在补偿前为-112.362 μm/m，补偿后为-10.677 μm/m，垂直度误差降低90.5%；X，Z两轴之间100 mm测量范围内的垂直度误差在补偿前为-141.465 μm/m，补偿后为-3.441 μm/m，垂直度误差降低97.6%。这表明面—线法得到的3项垂直度误差准确，可以有效保证其他项几何误差的准确辨识。

3个平面的测量现场如图9所示。在每个测量平面内，测量路径为相对测量参考点中心对称的100 mm×100 mm正方形测量区域的4条边和1条对角线。

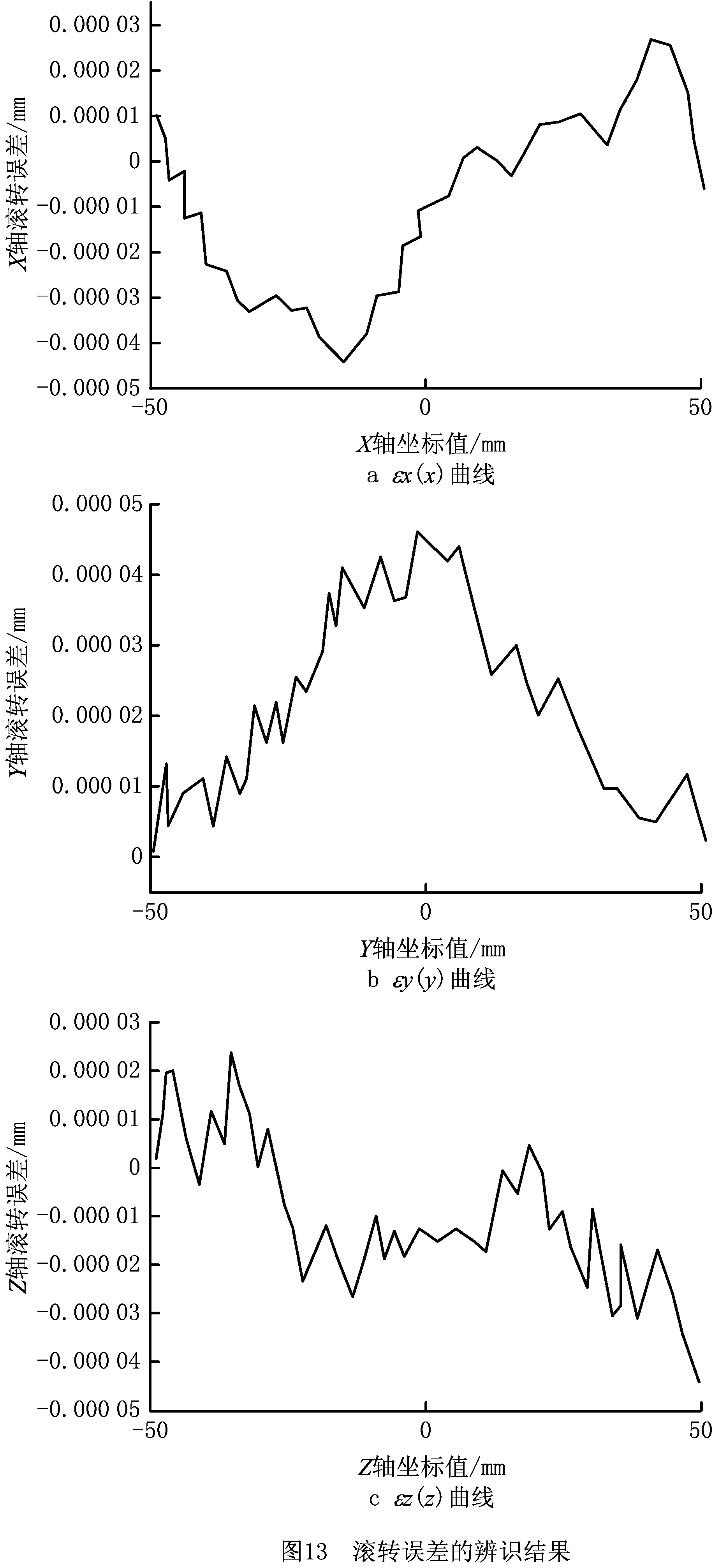
测量平面Ⅰ内的测量参考点坐标为(140.000,138.100,303.113)，测量平面Ⅱ内的测量参考点坐标为(100.000,138.100,225.000)，测量平面Ⅲ内的测量参考点坐标为(140.000,178.100,225.000)。为降低机床动态误差和热误差对测量结果的影响，令测量时的机床进给速度F=60 mm/min。根据设计的测量路径编写运行G代码，分别在机床的3个测量平面安装平面光栅，完成设计路径的误差测量，并记录测量误差数据。平面Ⅰ、平面Ⅱ和平面Ⅲ内的辨识结果分别如图10～图12所示，滚转误差的辨识结果如图13所示。

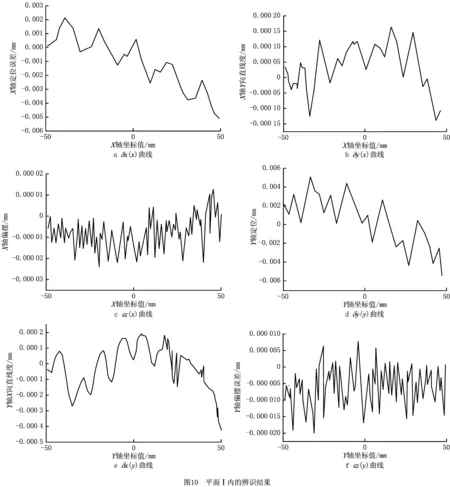
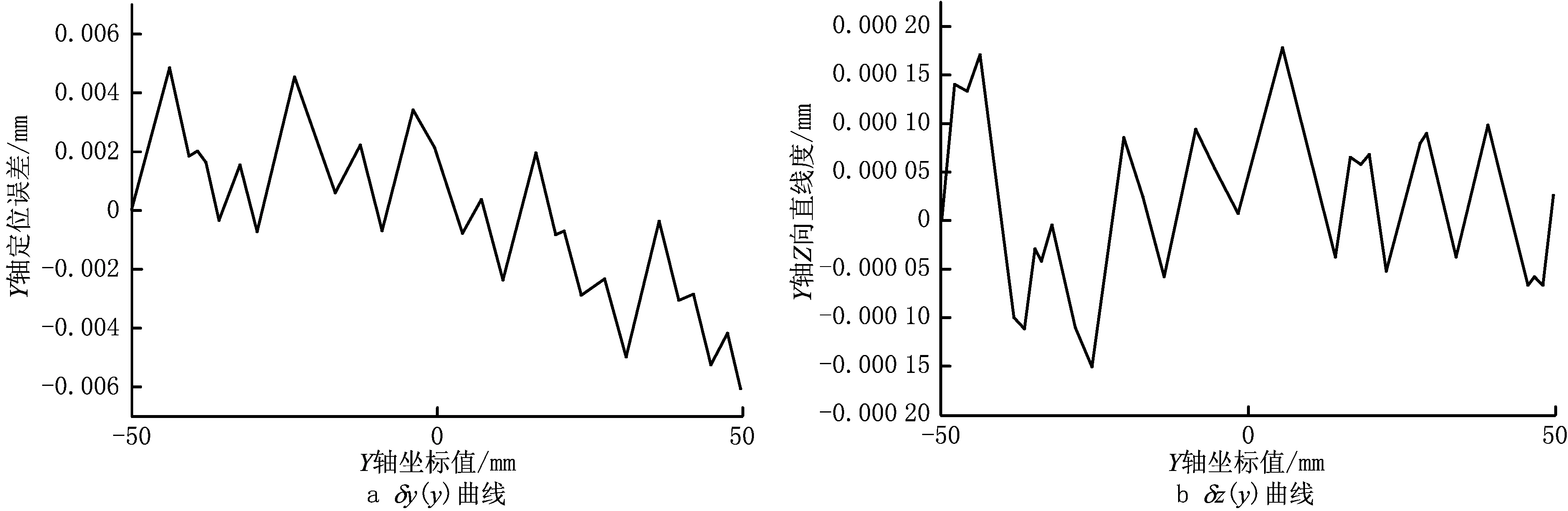
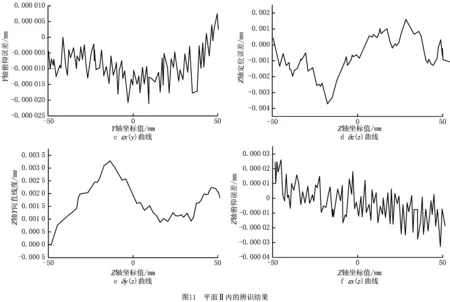
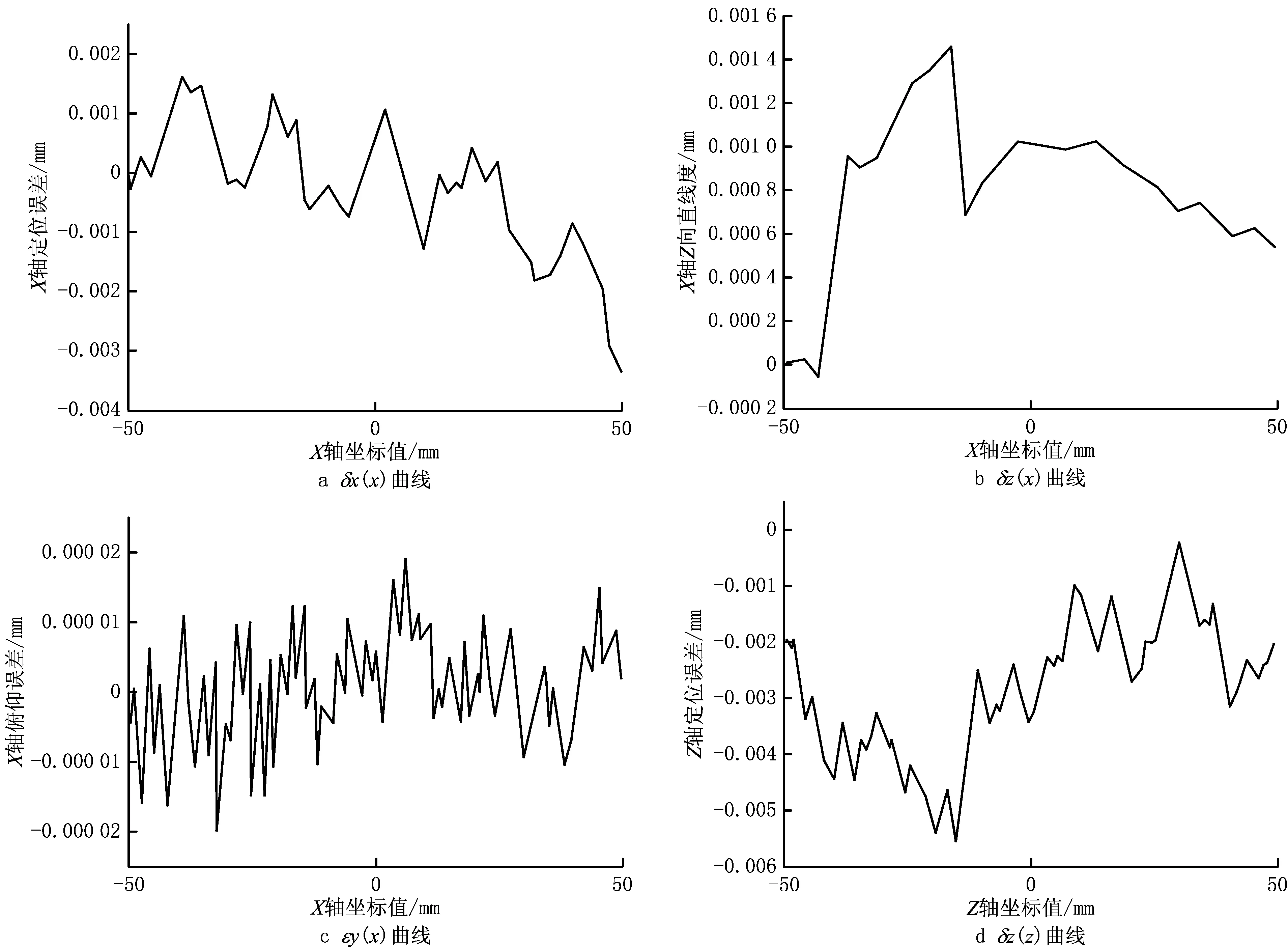
为验证面—线法测量结果的准确性，利用辨识值及综合误差模型(即式(12))对测量范围内的综合误差向量进行预测，同时利用九线法[19]在相同测量范围内进行几何误差测量和辨识，基于激光干涉仪的几何误差测量如图14所示。

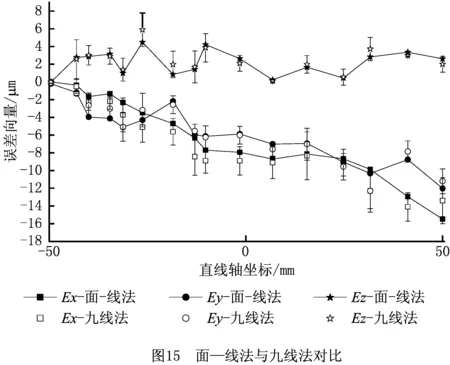
根据九线法辨识值计算三项误差向量值，结果如图15所示。由图15可知，基于面—线法的误差向量Ex，Ey，Ez与利用九线法的测量辨识值确定的误差向量变化趋势基本一致，面—线法的误差向量在九线法误差向量的分布区域内，两种方法的Ex，Ey，Ez之间最大偏差分别为2.4 μm，2.0 μm，1.4 μm，平均偏差为0.77 μm，0.61 μm，0.44 μm，偏差小于机床重复定位精度，说明测量结果的一致性较好，辨识结果有效。

4 结束语

本文根据目前机床检测精度高、速度快的要求，提出一种基于平面光栅的面—线精密机床空间几何误差测量和辨识方法，通过单轴和两轴联动在3个测量平面内分别连续测量一次直线轨迹，可快速实现三轴机床21项几何误差的准确辨识。该测量方法仅需3次安装，少于现有的利用激光干涉仪、球杆仪和平面光栅的几何误差测量方法，有效避免了安装误差对辨识结果的影响，高效精确的辨识方法可应用于工业现场三轴数控机床和五轴数控机床的精度评价。通过实验对比显示，基于面—线法的误差向量变化趋势与九线法结果一致，两种方法误差向量间的最大偏差为2.4 μm，平均偏差为0.77 μm，几何误差检测结果的精度较高。

本研究利用平面光栅检测任意平面内运动轴的轨迹精度，可实现几何误差的精确辨识，由于平面光栅测量范围有限，存在无法一次检测机床整个工作空间内几何误差的情况。另外，除几何误差以外，测量系统的安装误差与热误差是影响机床准静态精度和决定平面光栅测量精度不确定度的重要因素，溯源并降低以上两类误差对平面光栅测量方法的影响对进一步提升辨识精度、提高机床准静态精度具有重要意义，这也是后续研究的关键问题。