基于量化状态系统的多体系统动力学求解方法
2020-09-10李志华贺英良吴晨佳
李志华,贺英良,吴晨佳
(杭州电子科技大学 机械工程学院,浙江 杭州 310018)
0 引言
在机械、航空、航天、兵器、机器人等领域中,多体系统动力学为大量机械系统进行动态性能评估和优化提供了强有力的理论工具与技术支撑,是当今力学领域的研究热点和难点之一[1]。多体系统在运动过程中,由于不同构件之间的特性参数存在较大差异,或者柔性体大范围运动与构件本身较小弹性变形之间存在耦合,使得动力学方程呈现刚性,对这类刚性方程进行求解是多体系统动力学控制中的难点问题之一。
目前,多体系统动力学方程常见的数值解法有Newmark法、Wilson-θ法、Houbot法、Runge-kuta法和Gear法等[1-4],这些方法均基于时间离散的数值积分方法。当动力学方程为刚性,采用这些传统的数值积分方法求解时,为了保证求解过程稳定,需要强制使用隐式算法,因为所有显式方法都必须显著减少积分步长来确保数值的稳定性,而隐式算法需要在每一个积分步中调用迭代算法来解一个2n维的非线性代数方程组,其过程繁琐而复杂,计算成本随系统规模的增大显著增加[5]。
量化状态系统(Quantized State System, QSS)方法是一种新的数值积分方法,其与传统基于时间离散的积分方法明显不同,QSS对状态变量进行离散,即系统的状态变量以量子为单位跃迁,依次计算每次状态变量跃迁所需要的时间,从而推进积分。这一思想最早由Zeigler等[6]提出,并由Kofman等[7]首次实现。在求解一般动力学方程时,QSS不但具有稳定性强、精确度高等优点,而且计算过程完全不需要迭代,可以大大提升仿真效率[7]。
通过线性估计状态变量跃迁所需时间的方法称为一阶QSS方法。Kofman[8]后续又给出高阶的QSS2和QSS3算法,这些算法采用高次曲线估计跃迁时间来提高算法精度。然而作为一种显式算法,QSS在求解刚性系统时会出现仿真数值振荡现象(即不稳定现象)[9],因此不能完全应用于刚性系统。为解决这一问题,Migoni等[10]提出一阶后向QSS(Backward QSS, BQSS)算法,然而该算法精度不高(只有一阶精度),在非线性系统中,误差范围大可能会出现假性平衡点,使仿真无法正常进行。因此,近年来国外学者对QSS方法的改进从未间断,并将其应用于多个领域,例如文献[11]将其应用在建筑通风与空调系统仿真计算中,得到了较好的效果。
目前,国内只有北京航空航天大学的朱雨童等[12-13]和清华大学电机系的檀添、李帛洋、杨祎、秦建[9,14-16]等将QSS方法应用于具有间断和刚性的电力电子系统仿真求解中,并取得了一定的效果。
本文针对具有非线性和刚性特性的多体系统动力学,提出一种基于量化状态系统的多点校正(Multi-point Correction QSS, MCQSS)显式求解算法,该方法在保留QSS显式计算特性的同时,引入多点校正思想对状态变量导数进行修正,有效提高了算法的精度和稳定性。通过对多体系统的经典算例双摆进行仿真求解,验证了MCQSS算法的有效性,同时与传统数值积分方法、QSS方法和BQSS算法进行了性能对比。
1 量化状态系统方法
连续系统数值仿真需要离散化,例如Euler,Runge-kutta等传统方法是对时间进行离散,QSS方法是对状态变量进行离散,即将状态变量离散成一个个量子,计算状态变量由一个量化状态跃迁到另一个量化状态所用的时间,以此推进积分。需要说明的是,量子是事先给定的,类似于传统数值积分算法中的时间步长,量子的大小将直接影响求解的精度和速度。
连续系统的数学模型可用常微分方程组表示,将常微分方程组化为如下形式的状态方程:
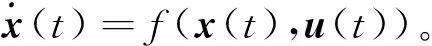
(1)
式中:x为状态向量;u为输入量。
对该系统进行量化处理,可得

(2)

(3)
式中:Δqj为状态变量的量子;εj为迟滞宽度,为了在不增加误差的条件下减少模型震荡,迟滞宽度εj与量子Δqj相同。
状态变量x各分量跃迁时需要变化的值为:
(4)
式中:qj为量化向量q的第j个分量;xj为状态向量x的第j个分量。

(5)
tj+1=tj+Δtj;
(6)
(7)
2 基于量化状态系统的多点校正显式算法
针对QSS方法无法求解刚性系统和BQSS算法精度不高、在非线性系统中仿真稳定性差的问题,提出一种MCQSS显式算法。该算法在QSS和BQSS的基础上,引入多点校正思想对状态变量导数进行修正,大幅提高了仿真中每步时间节点的精度,从而控制了误差范围,避免求解非线性刚性系统时出现扰动项,有效提高了算法精度和稳定性,同时保留了QSS方法显式计算无需迭代的特点,提高了算法的仿真效率。
假设动力学方程最终可化为常微分方程形式

(8)
相应经量化处理后可表示为

(9)

qj(t)=
(10)
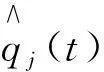
(11)
(12)

(13)


(14)
由3个修正值确定该段的拟合函数斜率最终值fj,
(15)
利用修正后的最终斜率确定状态变量此步的最终时间步长:
(16)
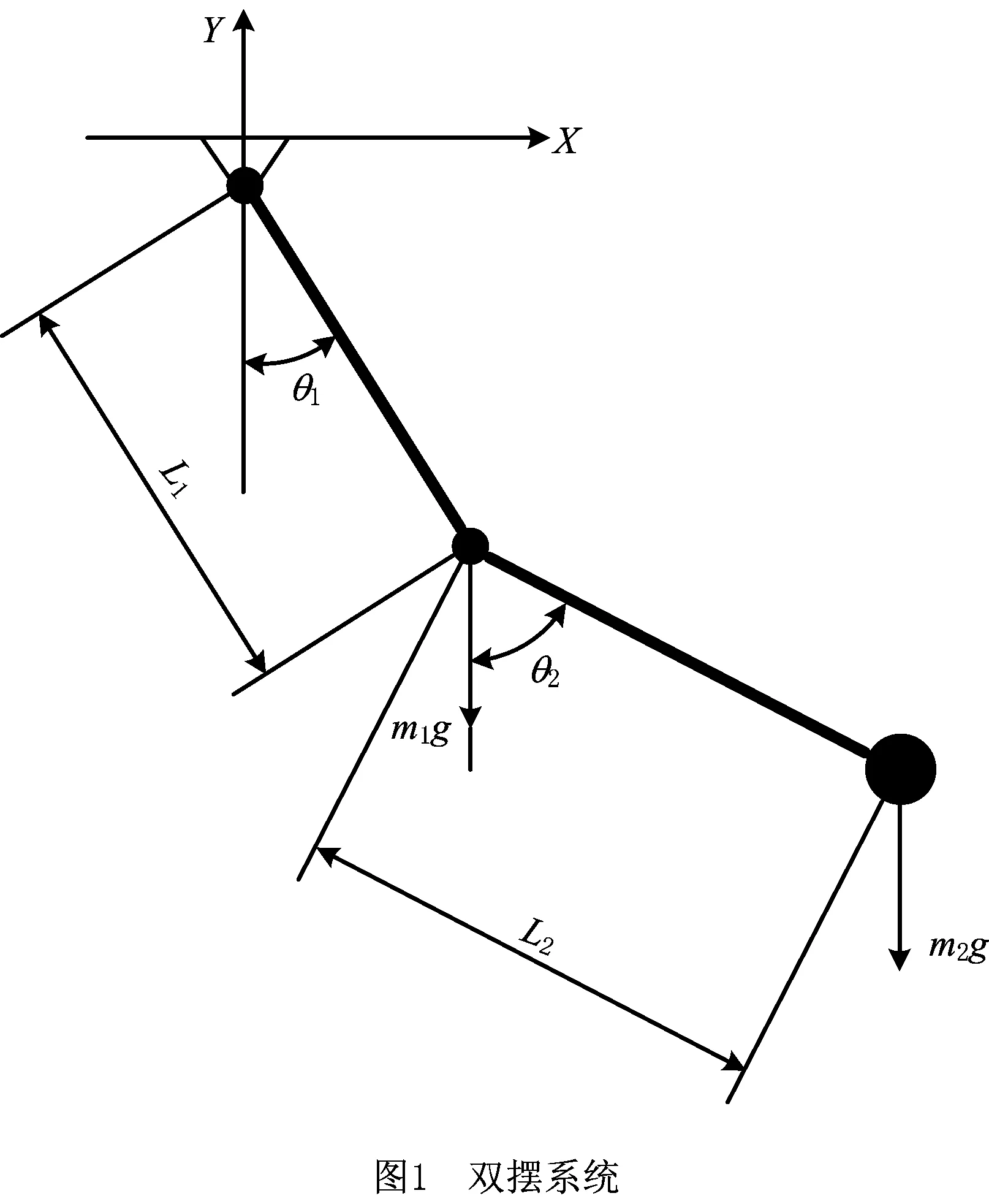
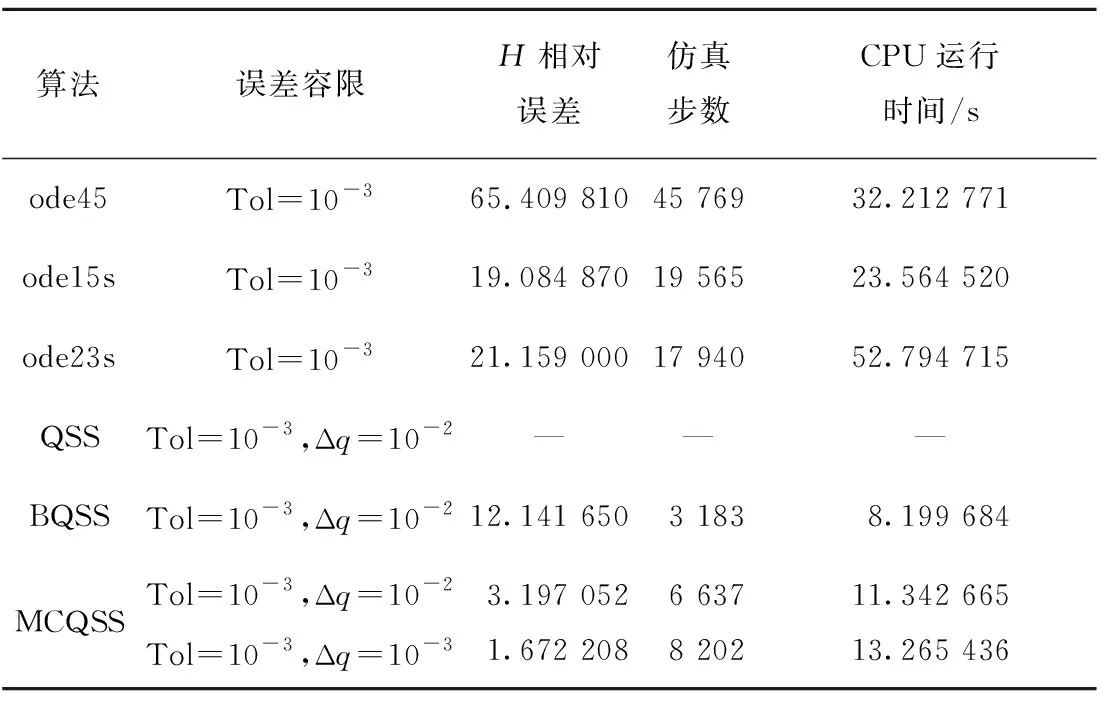
while(tj end if K1=f(tj,xj) Δtj=Δxj/fj//本步推进时长 end while 本章以典型多体系统双摆为例,将MCQSS算法与传统数值积分方法(ode45,ode23s,ode15s)、QSS方法和BQSS算法从仿真精度与仿真效率两方面进行性能对比。仿真条件如下: (1)计算机硬件配置为Intel i5-3427U处理器,CPU运行速度为1.80 GHz,操作系统为Windows 8.1。 (2)各算法均在MATLAB R2014b平台上实现。 (3)对所有的算法设置相同的误差容限,即Rel.Tol=Abs.Tol=10-3,同时将MCQSS算法中的量子大小分别设为Δq=10-2和Δq=10-3。 (4)总能量H的相对误差计算公式为 (17) 式中:u[k]为各算法求得总能量H的值;udassl[k]为微分代数系统求解器(Differential Algebraic System Solver, DASSL)算法在很小误差设定(10-9)下求的总能量H的值,在此作为基准值[17]。DASSL算法是一种使用后向差分公式的多步隐式求解方法,是求解刚性方程常用的时间积分方法。因为该方法需要使用牛顿法对差分方程进行迭代求解,虽然需要占用较大的资源且时间较长,但是精度较高[18],所以大多数仿真工具使用DASSL或其变种作为刚性方程的默认求解器[11]。 如图1所示的双摆系统,若m1和m2的质量相差悬殊,则可以使双摆系统动力学方程呈现刚性[19]。这里取m1=1 kg,m2=500 kg,两根摆杆长度l1=l2=1 m,不计重量。 采用拉格朗日方法对其建模,取系统的广义坐标q=[θ1θ2]T,则广义质量矩阵与广义力矩阵分别为: (18) (19) 式中θ1和θ2为两根摆杆与竖直方向所成的角度。 双摆系统的动力学方程为 (20) 系统的动能T、势能V和总能量H分别为[20]: (21) V=-m1gl1cosθ1-m2g(l1cosθ1+l2cosθ2); (22) H=T+V。 (23) 将该双摆系统的动力学方程式(20)化为如式(8)所示的常微分方程形式: (24) 对于本文的理想双摆系统(即不计空气阻力、铰链约束无摩擦),根据能量守恒定律,由给定的初始条件可知系统总能量始终保持为零。采用不同算法仿真双摆系统的总能量H,得到如图3所示的轨迹,其中QSS无解。由图3可见,DASSL的求解结果最好,MCQSS算法的结果较理想,其他算法精度较差。随着仿真时间的增加,它们的累积误差越来越大,特别是ode45,不但精度差,而且还会出现不稳定现象;MCQSS算法能将误差控制在一个较小的范围内,说明其精度和稳定性较好。 图3中,DASSL的求解结果最好,MCQSS算法的结果较理想,它们之间的异同之处如下: (1)DASSL算法是基于时间离散的数值积分方法,MCQSS算法是基于状态变量离散的积分方法。 (2)DASSL算法为隐式方法,在很小误差设定(10-9)下,得到图3中最好的结果(即精度最高),但计算时间长;本文方法为显式方法,在误差设定为10-3时,得到图3中较理想的结果(即精度较高),且计算时间短。 各算法对双摆系统总能量的求解结果如表1所示,可见QSS无解,说明其不适合求解刚性系统;相比ode45,MCQSS算法精度提高了20倍,效率提高了近3倍;相比ode15s和ode23s,MCQSS算法精度提高了近7倍,效率提高了1倍多;相比BQSS算法,在CPU运行时间相差不大的情况下,MCQSS算法精度提高了3倍多。 表1 各算法结果比较 为了研究量子大小对MCQSS算法性能的影响,分别设置了两个不同的量子值来仿真求解。由表1可见,当量子值减小时,CPU运行时间相差并不大,但是仿真精度却提升较多。 针对多体系统动力学刚性方程求解问题,本文尝试采用基于状态变量离散的积分方法,提出一种MCQSS显式算法,通过求解双摆系统动力学刚性方程得到如下结论: (1)ode45是显式算法,稳定性较差,很难兼顾仿真的精度和效率,且很难满足刚性系统在实际求解中的需要。 (2)ode15s和ode23s是传统数值积分方法中求解刚性系统较好的算法,本文MCQSS算法在仿真精度与仿真效率两方面比ode15s和ode23s更具优势。 (3)QSS方法不适合求解刚性系统,BQSS算法尽管能求解刚性系统,但其精度不如MCQSS算法,可见MCQSS算法中的导数修正值对提升精度是有效的。 (4)适当减小量子值能在几乎不增加仿真运行时间的同时有效提高仿真精度。 下一步将开展基于量化状态的混合系统求解方法研究,以扩展QSS方法的应用范围。


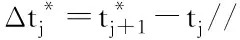
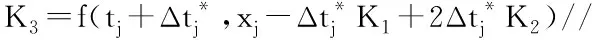
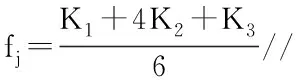

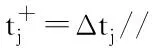
3 算例

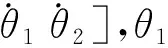


4 结束语
