基于改进粒子群算法的超声悬浮陀螺仪转子位置控制优化设计

朱 炼，盖昊宇

(1.安徽工商职业学院 应用工程学院，安徽 合肥 231131；2.哈尔滨工程大学 自动化学院，黑龙江 哈尔滨 150001)

陀螺仪是一种精密的惯性测量元件，其应用较为广泛。利用新的物理原理来设计新型陀螺仪，可以提高陀螺仪的精度和可靠性。目前已经投入使用新型陀螺仪主要有激光陀螺仪[1]、光纤陀螺仪[2]、静电陀螺仪[3]、微机电系统陀螺仪[4]等。

超声悬浮陀螺仪是一种利用超声波产生的悬浮力使陀螺仪转子悬浮的新型陀螺仪。该陀螺仪具有测量精度高、成本低的特点，具有广阔地市场前景。近年来，国外一些机构和学者先后开展了超声悬浮陀螺仪的研究[5-6]。Hiromi[5]等学者研究了超声波振动产生声场使转子悬浮的原理、行波通过粘性力诱导使转子旋转的原理以及转子运动误差；Takeshi[6]等学者进行了超声悬浮实验，初步设计了超声悬浮样机并计算出了悬浮刚度。我国也有一些学者开展了超声悬浮陀螺仪的研究[7-10]。陈耕潮[7]研究了超声悬浮陀螺仪的多物理场耦合，利用有限元法分析了定子和转子间的声场分布情况；陈超[8]等初步设计了超声悬浮陀螺仪结构并制造了样机，试验了其悬浮特性；李繁[9]对超声悬浮陀螺仪转子进行了设计优化，并进行了样机驱动实验；朱金冬[10]等详细设计了全自由度超声悬浮陀螺仪的三轴支承结构，在此支承结构的基础上，推导出了转子的悬浮力。这些国内外学者的研究多侧重于超声悬浮结构设计以及转子悬浮特性及悬浮力的计算，在转子位置偏移控制的设计中，主要是利用转子超声悬浮力的负支承刚度特性对其进行控制。这种利用超声悬浮力对转子位置进行控制，很难满足转子动态性能的要求。设计超声悬浮陀螺仪转子位置控制系统，对于提高陀螺仪的测量精度十分重要。

1 超声悬浮陀螺仪转子的声悬浮力分析

超声悬浮陀螺仪转子被密封在由三对球碗组成的超声支承鞍内，如图1所示，S1-S6为三对球碗状支承鞍，中间为球形转子。通过激励电源使球碗表面产生超声波，从而使转子悬浮。

图1 球碗状支承鞍

在平面声场的条件下，面积dS对转子的声辐射力为

(1)

式中ρ为空气的密度，c为声波在空气中的传播速度，l为超声振幅，d为悬浮高度，n0为面积dS法向单位矢量。

我们以x轴方向转子受力为代表来进行分析。根据文献[10]，在温度、空气密度以及超声振幅一定的情况下，处于图1所示结构的转子在x轴方向上受到的超声悬浮力为

(2)

式中d0为转子外表面与支承鞍间的额定间隙，R0为鞍体半径，S0为一块鞍体的面积，d为悬浮高度，θ、φ为球坐标系参数。

当转子的几何中心位于支承鞍内中心时，转子处于平衡。如果转子受到外界干扰使转子位置产生x轴方向偏移时，转子在x轴方向上受到悬浮合力为

(3)

此时，转子在x轴方向上的位置偏移Δx与超声悬浮力的关系为

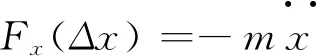
(4)

由于转子模型的负刚度特性，转子能够回到支承鞍内的中心位置。但为了使转子系统具有更好地动态性能，我们设计了控制器模块，并用改进粒子群优化控制器模块的参数。转子的位置控制回路如图2所示。

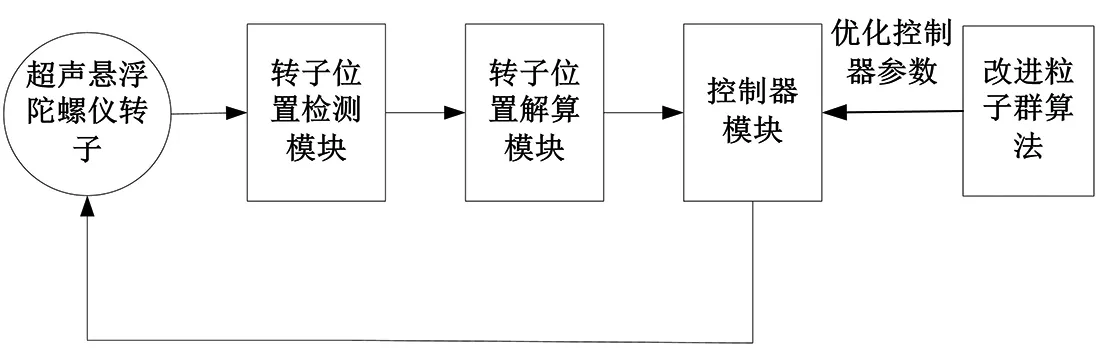
图2 转子的位置控制回路

2 改进粒子群算法

粒子群算法(PSO)是模拟鸟类觅食行为的一种启发式算法，其算法如下：

设m个粒子组成的种群为X=(X1,X2,···,Xm)，其中第i个粒子在N维空间的位置表示为Xi=(xi1,xi2,···,xiN)T。第i个粒子在N维空间的速度表示为Vi=(vi1,vi2,···,viN)T，其个体最优位置为Pi=(pi1,pi2,···,piN)T，gd为粒子群的最优位置。

在迭代中，粒子通过(5)、(6)式来进行速度和位置更新。

(5)

(6)

式中，k为当前迭代次数，vid为粒子速度，ϖ为惯性权重，d=1,2,···,N，i=1,2,···,m，c1、c2为学习因子，r1、r2为在[0,1]区间的随机值。

粒子群算法在迭代后期产生的粒子会越来越趋同，使算法的收敛变慢且难以得到全局最优解。我们对粒子群算法进行改进，改进粒子群算法能够较好地解决上述问题。具体如下[11]：

将(5)式调整为：

(7)

运用改进粒子群算法优化转子控制器参数的流程如图3所示。

图3 改进粒子群算法优化转子控制器参数的流程

3 算法仿真

转子控制器结构的数学模型为[12]：

(8)

以转子工作时工况条件最差的单位阶跃函数为干扰信号输入，采用改进粒子群算法优化转子控制器参数n(i)、d(i)。为了找到全局最优解，我们设代价函数为：

(9)

当转子受到外界单位阶跃干扰时，按照如下值选取改进粒子群算法的参数：种群数 s =50，N = 100，学习因子c1=2，c2=3，c3=0.7，惯性权重ϖ=0.6。迭代80次后，转子控制器参数的粒子更新在|n(i)|<0.65，|d(i)|<0.75范围内，代价函数值在0.03范围内，满足系统要求。同时，除了c3外，我们也按照上面值来选取粒子群算法的参数，来比较系统响应性能。

当转子受到外界单位阶跃干扰时，转子系统在无优化算法、粒子群算法和改进粒子群算法下，得到如图4所示的响应曲线。

图4 单位阶跃响应

从图3中可以看出，运用改进粒子群算法优化转子位置控制器参数后，单位阶跃响应的超调量由原来的约30%降低到约10%，粒子群算法也只能使超调量降到到约18%；而且运用改进粒子群算法，系统响应时间也明显减少。转子位置控制的动态性能明显改善。

4 结论

超声悬浮陀螺仪转子位置控制的动态性能是陀螺仪系统的重要性能，它能够直接陀螺仪的测量精度。根据超声悬浮陀螺仪转子和支承鞍的结构，分析转子所受的声悬浮力，设计转子系统的位置控制器。采用改进粒子群算法优化控制器参数，使转子系统阶跃响应的超调量、响应时间等动态性能明显改善，而且明显优于粒子群算法。同时也说明了改进粒子群算法的寻优能力好于粒子群算法。转子系统的动态性能的改善，有利于转子系统更快稳定，这对于陀螺仪系统有重要意义。