有色金属矿山安全生产风险预测系统研究

刘 兵，汪令辉，李全明，陈友良

(1.中国科技大学 计算机科学与技术学院，安徽 合肥 230027；2.铜陵职业技术学院，安徽 铜陵 244061；3.铜陵有色金属集团公司，安徽 铜陵 244000；4.中国安全生产科学研究院，北京 100012)

预测分析可以判断和推测未来事物的发展趋势，水平等。它在对象已知信息的基础上，利用各种定量的分析理论、方法，估计和测算事物未来的某些特征和发展状况[1]。预测分析是一种重要的工具，常常在通过事物的过去、现在的分析，来估计未来。在预测分析的基础上建立决策，可以有效的减少决策的盲目性。在矿山生产领域，其中占有重要地位的有色金属矿山安全生产，在它的风险预测实际操作中，首先确定预测目标，并抽取和预测目标相关的各个因素，对这些因素进行筛选、归纳。建立因素和预测目标之间的近似函数表达式，即确定数据模型。进行训练后，在安全生产风险预测中，输入因素特征值，即可得出相应的预测目标值，从而提供预测，为安全生产决策提供参考。

1 风险预测步骤

有色金属矿山风险预测的过程中，主要通过分析如下主要步骤来逐步实现：

1)首先要确定数据源，并根据需要，抽取待分析数据。

2)对抽取到的数据进行数据清洗、相关性分析、数据转换等方式的数据预处理。

3)利用训练数据，寻找合适预测方法，并建立预测模型。

4)利用测试数据对3)中生成的模型进行训练、并进行评估，并选出最优预测模型。

5)利用最优预测模型对目标进行预测预警。

具体风险预测流程的建立过程，如图1所示。

图1 有色金属矿山风险预测流程

2 模型数据

有色金属矿山安全生产的预测目标是矿柱的稳定性。

影响安全生产的风险因素归纳为这样几个方面：空区埋深、空区跨度、安全区规模、空区密集程度(单位区间内的空区个数)、空区存在时间、空区高度。

因素数据获取为安徽铜陵有色某大型矿山2017年下半年监测数据(不涉及泄密)，获取数据3572条，经过去燥、筛选，共得有效建模数据1293条。配置如图2所示。

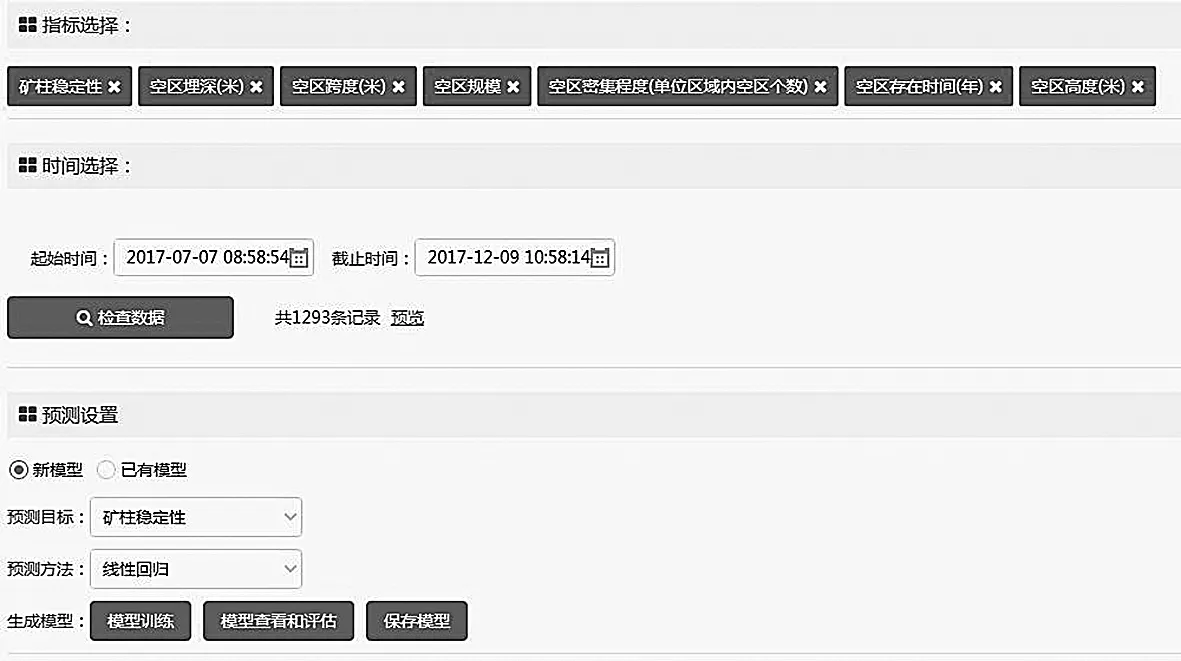
图2 安全因素及预测指标配置

3 风险预测建模及评估

比对数据和预测目标，在有色金属矿山的安全因素数据和预测目标之间，主要通过三种数据模型来进行评估，并根据数据训练的结果进行评估，选择合适的风险预测模型。

选择了三种模型来进行训练及评估比对：线性回归模型、BP神经网络模型和回归树预测模型。

3.1 线性回归预测模型

因变量和自变量之间的关系是直线型的称为线性回归模型，它利用线性回归方程可对所研究的现象进行预测和控制。它的公式如式1所示：

yi=ei+β1x1+β2x2+…+βpxp

(1)

线性回归方程是一个组合问题，已知一些数据，如何求里面的未知参数，给出一个最优解。在方程中将参数求解问题，转化为求最小误差问题，求出一个最接近的解。

模型与数据误差最小的形式是模型与数据差的平方和最小。这就是损失函数的来源。可以通过最小二乘法来求解这个函数[2]。

最小二乘法是通过误差平方和的最小化形式来匹配函数。如对于如式2的n组观察值

((X1,Y1),(X2,Y2),…,(Xn,Yn))

(2)

可以通过若干条曲线来拟合，如果能够选择通过样本数据中心的曲线，它的拟合误差(总残差)最小，那么就得到最佳拟合函数。

拟合误差可以通过残差和最小、残差绝对值和最小和残差平方和最小这三个指标来衡量。其中残差和存在之间的互相抵消问题，残差绝对值和的计算十分麻烦。残差平方和的计算比较容易，得到的值还具有良好的拟合性，所以选择残差平方和的形式来拟合曲线。计算的过程如下：

残差平方和达到最小的值为式3：

(3)

平方损失函数的值Q为式4：

(4)

(5)

(6)

从而求得平方损失函数的极值点。

在预测系统中将安徽铜陵某矿山的数据拟合，选择参与采空区矿柱稳定性预测分析的指标，并确定预测目标为矿柱稳定性，选择线性回归预测方法，然后开始训练模型。查看得到的线性回归模型信息，如图3所示，得到的误差值为0.12。

图3 线性回归模型信息

3.2 BP神经网络预测模型

B-P神经网络算法的网络结构是一个前向多层网络，它将学习过程分为“正向传播”和“误差的反向传播”，原理如图4所示。样本数据从正向到输出层的传播过程中，如果不符合期望值，就转为反向传播[3]。“误差的反向传播”过程中，将误差在各个单元上逐层分摊，并获取各层误差，同时将此作为修正的数据。“正向传播”和“误差的反向传播”循环多次进行，直到获取最小误差为止[4-6]。

图4 B-P神经网络原理图

在预测系统中将安徽铜陵某矿山的数据拟合，选择参与预测分析的指标，并确定预测目标。选择神经网络预测方法，然后开始训练模型，如图5所示。

图5 神经网络模型配置Figure 5 Neural network model configuration

查看得到的神经网络模型信息，如图6所示。BP神经网络预测模型得到的误差为0.13。

图6 神经网络模型信息Figure 6 Neural network model information

3.3 回归树预测模型

决策树是最广泛的数据模型之一，它采取自上而下的形式，每一个结点采取最佳的属性，并对树进行裁剪，从而训练出合适的模型。其中CART(分类回归树，Classification And Regression Tree)是一种重要的决策树模型[7-9]。它既可以用于创建分类树，也可以创建回归树。

CART创建分类树的过程中，将最小Gini(基尼指数)信息增益作为特征结点划分决策树。用熵来度量决策树的决策选择过程的ID3算法及其改进的C4.5算法能够尽可能的挖掘信息，但生成的决策树分支多，规模大。另外，为了避免过度拟合，还需要对CART树进行裁剪。预测时，将特征值和决策树的叶子节点匹配，即可得到预测类别[10-11]。

CART回归树观察值是连续的，可以通过训练数据在树中得出的值创建预测规则[10]。但在这各情况下，不能进行最优划分，所以要用到最小剩余方差(Squared Residuals Minimization)来进行回归树(Regression Tree)的划分。通过最小剩余方差的划分可以使子树的误差方最小。创建模型树时，如3.1所述，每个叶子是一个线性回归模型。

在预测系统中将安徽铜陵某矿山的数据拟合，选择参与预测分析的指标要求，并确定预测目标。选择回归树预测方法，然后开始训练模型，如图7所示。

图7 回归树模型配置Figure 7 Regression tree model configuration

查看得到的回归树模型信息，如图8所示，误差值为0.09。

图8 回归树模型信息

4 模型选择与模型预测

4.1 模型选择

通过3中对线性回归模型、BP神经网络模型和回归树预测模型三种模型下，安徽铜陵某矿山安全预测模型的计算。在不同的预测方法下，数据得到不同的预测模型。

根据实验分析，可以得出在上述示例中，线性回归预测模型、BP神经网络预测模型、回归树预测模型预测分析的误差分别为0.12、0.13和0.09，可以得出误差最小的是回归树模型。因此安全生产风险预测模型选择误差最小的回归树模型作为最优预测模型。

为了验证预测模型，将安徽铜陵有色某矿山最新监测指标数据输入到训练好的有色金属矿山指标预测模型，模型会实时给出最新的预测结果，显示预测值为0.2。预测结果可以用于预警以及辅助决策，如图9所示。

图9 模型预测

4.2 模型选择分析

回归树预测模型取得比线性回归预测模型、BP神经网络预测模型更小的误差，分析主要是如下的原因：

1)线性回归模型是简单易用的预测模型，通过自变量和因变量的关系来拟合曲线，但由于影响因子的多样性、变化性和复杂性，对于比较复杂，庞大的数据，线性回归就不是很准确。有色矿山安全预测中，提供预测因素的多样，数据复杂、庞大，这些因素导致线性回归预测误差不如另外两种模型。

2)BP神经网络对复杂的数据建模比较有优势，但它对训练数据的要求比较庞大，只有用大量的数据进行训练后，才有较高的准确性，本文提供的数据对BP神经网络模型的训练可能不够，所以它的误差比回归树模型要大一点。

3)回归树对复杂的非线性关系有较大的优势，适合于较复杂的模型，且进行合理的修剪后，拟合度更高。

因为上面的原因，采用回归树预测模型进行学习后，经过验证，可以更好的进行有色矿山安全生产风险模型的建立。

5 结束语

矿山安全生产事关重大，关计国计民生，通过挖掘原有数据，并在此基础上建立风险预测模型，可以有效增加生产，保障矿山安全生产。本文利用有色金属矿山监测数据，通过回归预测模型、BP神经网络预测模型、回归树预测模型三种建模的比较，选择回归树模型作为安全生产风险预测模型，通过以上研究分析，可以得出如下结论：

1)在线实时数据监测和网络数据抓取是有色金属矿山企业安全生产风险数据获取的两种主要方式，通过数据提取、挖掘分析、建模应用等操作步骤完成有色金属矿山企业安全生产风险预测[12-14]。

2)文中采取线性回归预测模型、BP神经网络预测模型、回归树预测模型三种预测分析并进行比较，选择误差最小的回归树模型作为最优预测模型，能更加准确地得到预测结果。

3)矿山除了自然资源的矿藏外，生产数据也是一个具大的宝藏，要充分利用和挖掘这个宝藏，对于保障生产有着重要的作用。

4)下一步还要进一步利用这些数据，对于生产的时间，效率，产量等进行决策支持。