开关磁阻电机损耗计算研究综述
2020-09-10刘寅遐朱学忠卢迪墨杨姗姗
刘寅遐,朱学忠,卢迪墨,周 洲,杨姗姗
(南京航空航天大学 自动化学院,南京 210016)
0 引 言
开关磁阻电机(Switched Reluctance Motor:SRM)是一种典型的机电一体化调速电机,其调速系统兼具直流调速系统和交流调速系统的优点。该电机具有制造成本低、坚固可靠、结构简单、方便维护、可控参数多,在宽广转速、功率范围内输出高、效率高及容错性好等优点。目前,研制的几十瓦到千瓦级的开关磁阻电机已成功广泛应用于风力发电、车辆牵引、卷扬机和泵等工业领域[1]。
但由于其电机铁心不同部分的磁通各不相同,且存在高度的局部饱和现象,致使开关磁阻电机性能分析较为困难,给铁损的计算及热分析带来了很大的难度[2]。上世纪80年代末,就有开关磁阻电机铁心损耗相关计算的文章发表[3],本文查阅了大量关于开关磁阻电机损耗的国内外文献,将对开关磁阻电机的损耗计算进行综述。
开关磁阻电机的损耗主要包括铜线损耗、机械损耗、杂散损耗和铁心损耗。
1 铜线损耗分析
开关磁阻电机损耗的重要组成部分,由于开关磁阻电机中的电流波形不是正弦波,因此比较难以精确估算不同转速下开关磁阻电机的铜损耗。其电流波形主要取决于励磁电流、速度和开关策略等工作条件[4]。
常规电机的铜线损耗包括基本铜损耗和附加铜损耗。基本铜损耗是指电流流经定子绕组和转子绕组时所产生的焦耳热;附加铜损耗是由交流电在定子绕组上发生的趋肤效应和邻近效应引起的额外损耗以及定子绕组各股线之间循环电流引起的杂散铜损耗[5],但开关磁阻电机只有定子上装有绕组,转子上没有绕组,所以只有定子上产生铜线损耗,转子不产生铜线损耗。
开关磁阻电机稳态运行时,忽略绕组表面的集肤效应,可用以下公式计算绕组铜损[6]:
(1)
式中,q为电机相数,Irms为一相绕组电流的有效值,RP为相绕组的电阻。
若相电流波形已知,则相电流的有效值可按下式计算:
(2)
式中,Nr为转子齿数,θon为开通角,θp为关断角。
除了以上公式进行铜线绕组的粗略计算,目前主要使用有限元法对绕组铜损进行计算。其中,文献[7]提出一种可以快速建立有限元模型并自动模拟SR电机的方法,文献[8]对提出的二维模型在允许的精确范围内,能够快速计算出绕组铜损,文献[9]针对不同控制策略下的绕组损耗进行了分析,并通过对比发现,将绕组定位在定子磁轭上,可以减小交流铜损耗,文献[10]提出的基于微扰法的二维模型简化方法,可以精确快速地计算机器铜损耗。
2 铁心损耗
开关磁阻电机是一种特殊的双凸极结构,其铁心磁场变化规律复杂,铁心的不同部位磁通密度不同,存在着很高的局部饱和现象,供电波形复杂,工作在步进状态,无法用常规方法计算其损耗[11]。
2.1 实验法
铁损值可以用实验的方法近似测量,这也是测量开关磁阻电机铁损值最早的方法。
2.1.1 基于傅里叶分解法的实验法
对电机中在不同频率、不同幅值的正弦磁场中的铁损进行测量,总结成铁损密度与磁场频率和幅值关系的查找表W(B,f),然后通过磁路分析或有限元分析得到铁心的磁密波形,再通过傅里叶分解得到磁密谐波的振幅和频率,最后通过查找表W(B,f)求出各次谐波对应的铁损,从而求和得到电机铁心的总损耗。总涡流损耗和总磁滞损耗分别用以下公式估算:
(3)
式中,Wei为第i个单元单位体积铁心的涡流损耗,Whi为第i个单元单位体积铁心的磁滞损耗,Vi为第i个单元的体积,Bk为第k次谐波的磁密幅值,fk为第k次谐波的频率,n为计及的最高次谐波次数,N为铁心总单元数目。
2.1.2 基于磁密峰值法的实验法
在对电机铁损计算精度要求不高的情况下,可以仅考虑铁心磁密波形的基波,忽略谐波的影响,通过实验的方法测得铁心在基频磁密峰值下的涡流和磁滞损耗密度,总结形成能体现单位体积铁心损耗与磁场频率和幅值关系的查找表W(Bmax,f),则总涡流损耗和总磁滞损耗可通过以下公式估算:
(4)
式中,Bmax为磁密峰值,f为磁密频率。
基于磁密峰值法的实验方法只需要在基波频率下测量不同幅值正弦磁场中的铁损,其工作量小于傅里叶分解法,但由于它不考虑磁密谐波分量对铁心损耗的影响,所以其计算精度低于傅里叶分解法。这两种方法都是通过实验的方法来测量不同正弦磁场下的电机铁损值,都难以精确测量,因此在计算电机铁损时较少采用实验法。
2.2 数值计算法
2.2.1 损耗分离模型
铁损的产生过程非常复杂,对其进行精确计算十分困难,文献[12]中Krishnan及Materu假设定子磁通波形是三角波,将傅立叶分解用于分离开关磁阻电机铁损的基波分量和谐波分量,推导了电机不同部位磁通频率的一般表达式,并得出铁心损耗主要发生在转子内部且为励磁电流和速度的函数的结论。文献[13]中Hayashi和Miller提出一种将铁损分为磁滞损耗与涡流损耗,该模型中磁路不同部分的磁通关系由基于Krishnan-Materu模型的矩阵形式给出,涡流损耗通过改写STEINMETZ方程求得,磁滞损耗是基于单极磁密波形由实验方法确定。
在此基础上,Bertotti等提出了目前工程上广泛应用的损耗分离模型,即按铁损产生机理将其分为涡流损耗Pe、磁滞损耗Ph以及附加损耗Pc三部分,具体模型[14-19]:
PFe=Pe+Ph+Pc
(5)
式中,PFe为单位体积的总铁损(W/m3),Pe为单位体积的涡流损耗(W/m3),Ph为单位体积的磁滞损耗(W/m3),Pc为单位体积的附加损耗(W/m3)。
在低频中等磁场和强磁场中,铁损主要由涡流损耗和磁滞损耗组成,因此,在计算铁心损耗时常常忽略附加损耗Pc的影响。
文献[20]在计算SR电机铁损时,对定转子轭部和极部的磁密波形进行分解,提出了一种改进的Steinmetz方程。
2.2.2 椭圆旋转模型
在实际中,电机定子铁心的磁化方式较为复杂,不同位置的磁化方式各有差异,既包含交变磁化,也包含圆形旋转磁化,因此我们将其称为椭圆形旋转磁化。
在圆形旋转磁场中,铁磁材料的磁滞损耗在起始时随着磁感应强度的增加而增加,但磁感应强度到达一定值时,磁路饱和,旋转磁滞损耗开始下降。而交变磁滞损耗则没有下降的现象。图1为日本学者T. Matsuo等实验测得的50A 1300 硅钢片两种磁滞损耗曲线[21-22]。

图1 50A1300硅钢片的旋转磁滞损耗和交变磁滞损耗
旋转磁滞损耗的特性规律是基于大量实验总结得出的,目前尚未完全弄清其内在机理,J.G. Zhu等人经过大量实验,采用曲线拟合的方法,建立了圆形旋转磁化损耗模型[23]:
Pr=Phr+Pcr+Per=Phr+Kcr(fBm)2+Ker(fBm)1.5
(6)
式中,Pr为铁心损耗(W),Phr为磁滞损耗(W),Pcr涡流损耗(W),Per为附加损耗(W),Kcr为涡流损耗系数,Ker为附加损耗系数。
其中,磁滞损耗Phr可用如下表达式模拟
(7)
式中,Phr为圆形旋转磁化条件下的磁滞损耗(W),Bm为旋转磁密幅值(T),Bs为材料的饱和磁密(T),a1、a2、a3为和材料有关的系数,S是硅钢片的截面积(m2)。
当椭圆短轴为零时,为交变磁化,当短轴与长轴相等时,为圆形旋转磁化。下式为计算铁损的椭圆旋转模型:
Pt=Pth+Ptc+Pte
(8)
式中,Pth为总磁滞损耗(W),Ptc为总涡流损耗(W),Pte为总附加损耗。
其中
(9)
式中,Phrk为k次磁密谐波按圆形旋转磁化计算的磁滞损耗(W),RBK为k次磁密谐波椭圆形轨迹中的短轴和长轴之比(RBK=Bkmin/Bkmaj),Phak为k次磁密谐波按交变磁化计算的磁滞损耗(W)。
(10)
式中,Kca为交变磁化涡流损耗系数,Bkmin为k次磁密谐波椭圆磁场的短轴(T),Bkmaj为k次磁密谐波椭圆磁场的长轴(T)。
(11)
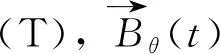
椭圆旋转模型具有较高的计算精度,但在计算前需要通过二维铁损测试设备得到在圆形旋转磁化和交变磁化条件下铁磁材料的损耗曲线来对照拟合相关的系数。而目前而言,仅在少数大学和研究所拥有二维铁损测试设备,因此损耗系数难以获得,影响了该方法的推广与应用。
2.2.3 正交分解模型

(12)

该方法将谐波磁场和旋转磁场都考虑在内,其损耗系数可通过硅钢片厂家提供的损耗曲线(交变磁化方式下)拟合得出,易实现、精度高。
此外,文献[27] 提出了基于铁心损耗与相位的等效电路模型,以使得计算结果更为准确。文献[28]采用考虑了小滞环的磁滞损耗计算数学模型进行计算,对于涡流损耗,在采用传统正弦磁通波形计算公式的基础上,加上涡流损耗修正因子计算。
在铁损计算中,有限元法也应用得十分广泛,文献[29]采用有限元法对四相开关磁阻电机的磁场模式进行了分析研究,阐述了各部分铁心中磁场变化周期及规律,并借助谐波分析方法估算了电机铁心损耗。文献[30]提出了一种通过有限元分析来确定磁通波形的高速开关磁阻电机铁损测量方法。
SR电机的磁场与其电机结构、控制方式、绕组连接方式均有关系,关于各种不同工况的SR电机铁心损耗研究,将成为今后的研究重点。文献[2]研究了不同绕组连接方式下,SR电机铁心损耗的情况。文献[31]分析了在滞环电流控制和单脉冲模式下,定、转子区域的磁通密度波形和铁心损耗。文献[32] 研究了不同类型的短节距绕组布置以及不同铁心叠片材料对开关磁阻电机铁损的影响。文献[33]提出了一种相位间强耦合开关磁阻电机的铁心损耗计算方法。文献[34]研究了一种新型无轴承开关磁阻电机的铁心损耗特性。
3 机械损耗分析
机械损耗分为轴承损耗和风摩损耗,轴承损耗是由转轴和轴承之间的机械摩擦造成的,可以通过改善轴承与转轴之间的润滑等措施来减小损耗;风摩损耗是电机旋转过程中转子表面与空气之间的摩擦所造成的,可通过改变转子结构,减小转子表面与空气的接触面积等措施来减小风摩损耗。
机械损耗表达式为:
Pfw=aw×V×ωq
(13)
式中,aw为风阻系数,V为不考虑定子部分的空气体积,q为曲线拟和参数,ω为角速度。
不同电机的风阻系数差异也很大,这与电机的装配方式、负载和运动等因素有关,这些系数通常是由电机的实验结果推出。在计算机械损耗相关系数的实验中,主要采用的方法是测量励磁电源关断后的电机减速率[35]。图2为测量未知系数的具体过程,首先使电机空载运行,达到一定转速后,断开励磁电源,记录减速率产生的转矩和功率,测量得到电机转子转速的变化率,从而得到机械损耗与转速间的关系曲线,再利用曲线拟合方法,来求得轴承损耗和风摩损耗的变化曲线,最后,推导出公式(13)中的未知系数。
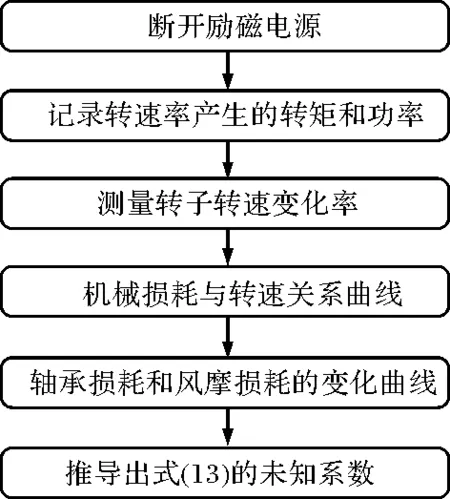
图2 公式中未知系数的求解过程
单个电机之间存在差异,其机械损耗系数差异也很大,因此公式(13)仅适用于计算同一样机在不同转速下的机械损耗。该公式在样机的设计过程中意义不大,只能用于校验设计样机的机械损耗。
4 杂散损耗分析
杂散损耗的产生与漏磁、相电流分布不均匀、气隙磁通分布不规则以及气隙中的机械缺陷等因素密切相关,计算较为复杂,目前尚没有精确的杂散损耗计算公式。在电机设计过程中,杂散损耗可近似为总损耗的6%[36]。开关磁阻电机的杂散损耗计算公式如下:
Ps=(P1-P2)×6%
P1=T1·Ω
P2=U2·I2
(14)
式中,P1为原动机输给电机的机械功率,P2为发电机输给负载的功率,T1为原动机输出的转矩平均值,Ω为原动机旋转角速度,U2为输出直流电压平均值,I2为功率变换器输出电流平均值。
5 结 语
开关磁阻电机近年来发展迅速,损耗分析对于电机而言,在提升性能、增强可靠性等方面扮演者重要的角色。本文对开关磁阻电机的损耗计算方法进行了综述,介绍了电机中铜线损耗、铁心损耗、机械损耗、杂散损耗四种损耗方式,其中着重对铁心损耗的实验法和数值计算法进行了说明。
