基于NSGA-Ⅲ的开关磁阻发电机多目标优化设计

李 洁，李艺辉，刘作军

(河北工业大学 人工智能与数据科学学院，天津 300132)

0 引 言

开关磁阻发电机(Switched Reluctance Generator, SRG)因具有结构简单、坚固，成本低，低速运行性能好，可控参数多，高容错性等诸多优点，在风力发电[1]、航空航天[2]等领域具有十分广阔的应用前景[3]。

由于SRG存在转矩脉动大、噪声大等问题，SRG的实际应用受到限制。为解决SRG转矩脉动较大的问题，国内外学者在SRG本体设计参数[4]、控制参数[5]优化等方面进行了大量研究。一般而言，SRG需优化多个性能指标以保证发电机全面高效的运行性能，因此，SRG多目标优化方法的研究具有重要意义[5]。

目前，电机多目标优化方法主要包括传统的多目标优化方法和基于进化算法的多目标优化方法[6]。其中，传统的多目标优化方法主要通过评价函数法[7-8]、目标规划等方法将多目标问题转化为单目标问题求解。但是，在SRG多目标优化设计中，由于优化目标间相互制约，采用传统的多目标优化方法得到的最优解无法使多个优化目标同时达到最优。而基于进化算法的多目标优化方法通过寻优得到一个Pareto解集，决策者可从多组优化方案中依据偏好选择最优解，弥补了传统多目标优化方法的不足。基于遗传算法的多目标优化进化算法具备遗传算法较强的全局搜索能力和鲁棒性[9]。其中，快速非支配排序遗传算法(NSGA-Ⅱ)引入了拥挤度和精英策略保持了种群多样性，提高了电机优化的精度和效率[10-11]。但是，改善了种群分布的改进NSGA-Ⅱ[13]无法正确估量三目标及三目标以上优化问题的拥挤程度，在优化3个及以上目标的电机优化设计中存在不足。因此，文献[13-14]提出一种基于参考点的非支配排序遗传算法(Non-dominated Sorting Genetic Algorithm Based on Reference Point, NSGA-Ⅲ)，以参考点与种群的关联操作代替NSGA-Ⅱ的拥挤度选择机制，可从精英策略方面更好地解决包含3～15个优化目标的多目标优化问题。

本文提出一种基于NSGA-Ⅲ的SRG多目标优化方法，利用响应面法(Response Surface Methodology, RSM)对SRG的优化目标进行回归建模，在保证拟合精度的基础上采用NSGA-Ⅲ对SRG结构参数和控制参数同时进行优化，通过全局寻优得到Pareto最优解集，为决策者提供多种解决实际工程问题的优化方案。

1 SRG初始设计

本文依据SRG设计方法[15]计算得到如表1所示的1kW四相8/6极SRG样机的主要设计参数。

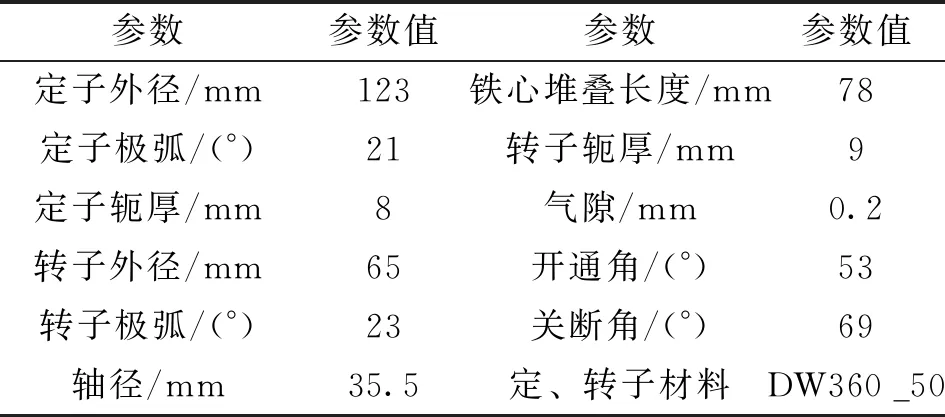
表1 四相8/6极SRG初始设计尺寸

利用Ansys/Maxwell软件对SRG模型进行有限元静态及瞬态仿真分析，得到恒功率额定工况下SRG的性能如表2所示。

表2 额定工况下的SRG性能

2 SRG性能参数化分析

运用Maxwell软件对SRG转矩脉动、效率、功率密度进行参数化分析。各参数设定如表3所示的初值，通过有限元仿真得到定子极弧βs、转子极弧βr、定子轭厚Ys、转子轭厚Yr、定子内径Dsi、开通角θon、导通角θc变化对SRG性能的影响，如图1所示。

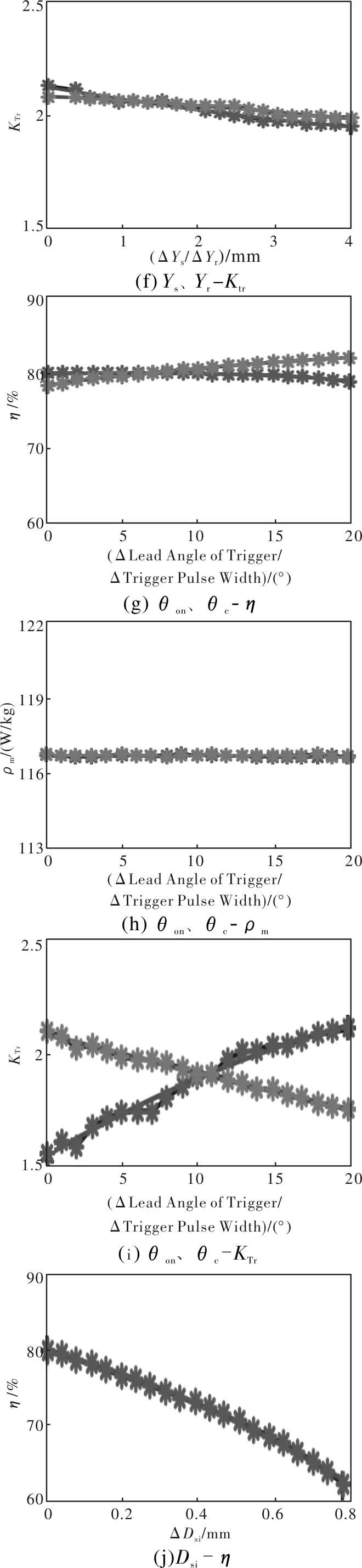
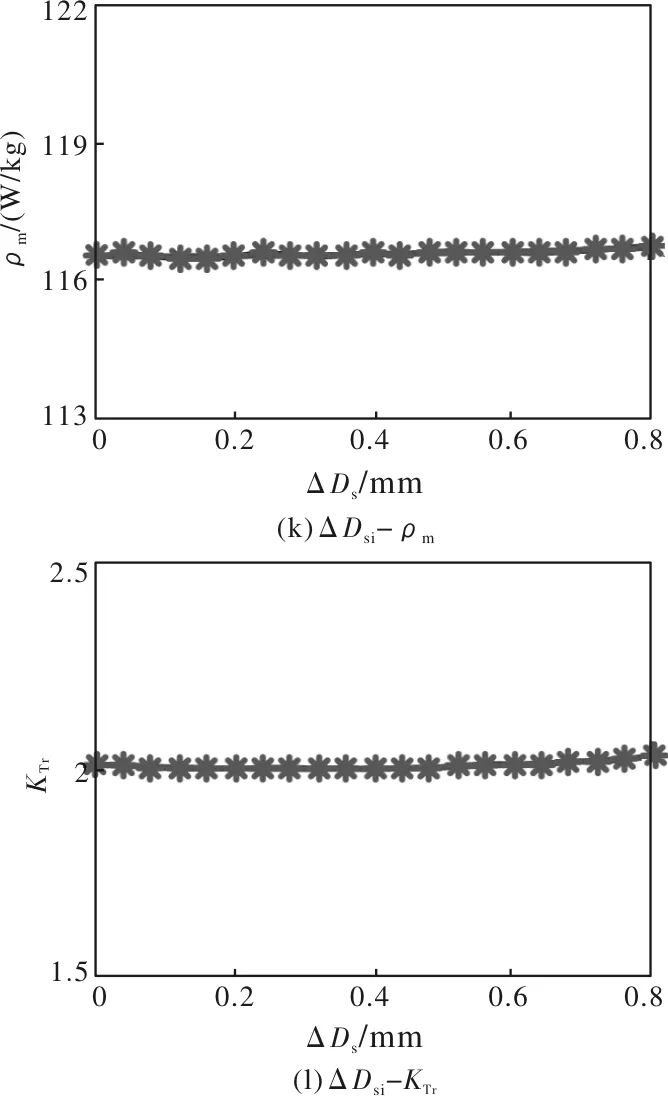
图1 SRG参数对发电机性能的影响

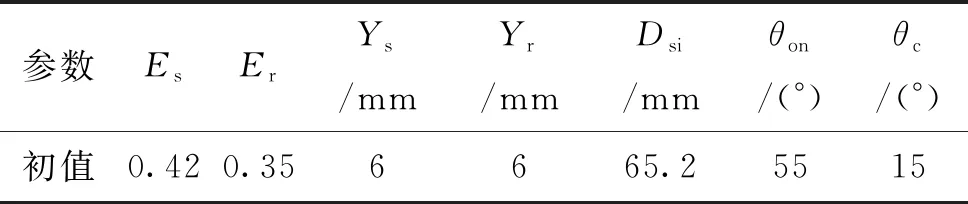
表3 参数化分析的初始值设置

图1直观反映了各参数变化下SRG性能的变化趋势。图1(d)中，发电机效率分别随Ys的增大、Yr的减小而增大，在额定功率附近1%的范围内变化；图1(h)、图1(k)中，随θon、θc的增大，SRG功率密度在额定值附近0.1%范围内变化；从图1(a)、图1(g)、图1(j)中可以得到，转子极弧系数Er大于0.4会导致发电机效率降低，随着气隙增大，效率呈线性下降趋势，适当增大θc及Ys使发电机效率呈现小幅度增大趋势；图1(e)、图1(f)中，Ys、Yr增大时，发电机质量增加，恒功率工况下SRG功率密度和转矩脉动随着轭厚增大呈线性减小趋势；图1(c)、图1(i)中，增大βs使得转矩脉动增大，转子极弧系数超过0.42时会增大转矩脉动；随着θon的减小、θc的增大，转矩脉动减小，提高了发电机的运行性能。

3 基于NSGA-Ⅲ的SRG多目标优化设计

3.1 优化目标及优化变量

为满足SRG高效稳定的运行需求，本文求解SRG多目标优化问题：

(1)

式中，η(x)为SRG效率；ρm(x)为SRG功率密度；KTr(x)为SRG稳定运行周期内的转矩脉动系数。

考虑到定子极磁密对SRG运行铁耗的影响，铁心轭部的结构强度以及发电机运行过程中的温升和铜耗等因素，设置定子极磁密Bps、定子轭部磁密Bcs、定子绕组电流密度JCu满足式(1)中的性能约束。

通过对SRG的参数化分析，选取对发电机性能影响较大的参数为优化变量：定子极弧βs、转子极弧βr、定子轭厚Ys、转子轭厚Yr、定子内径Dsi、开通角θon及导通角θc：

X=[x1,x2,x3,x4,x5,x6,x7]T

(2)

3.2 SRG优化目标的响应面建模

采用中心复合试验设计(CCD)[16]方法进行优化变量的5水平采样，通过Expert Design软件得到采样结果如表4所示。

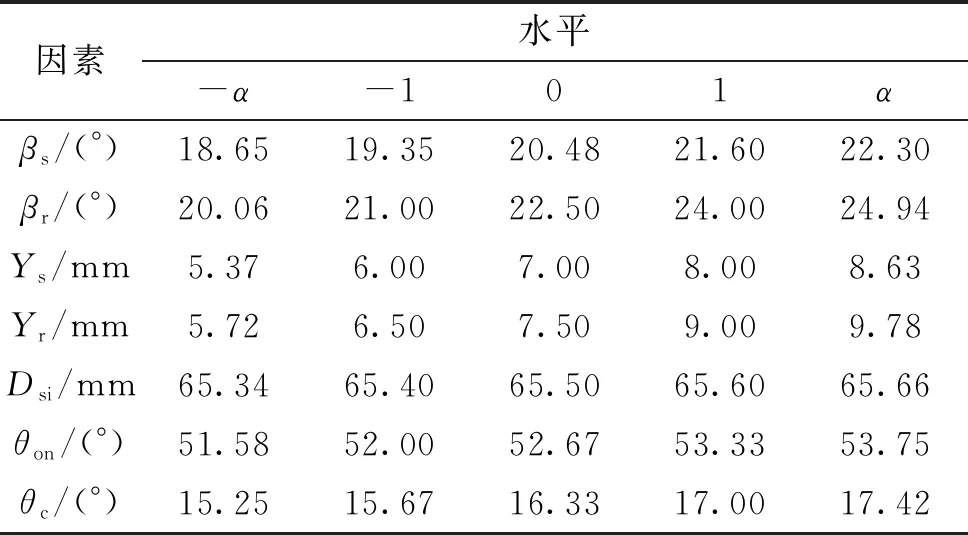
表4 因素及水平参照表

利用Maxwell软件对不同水平下的参数组合进行有限元仿真分析得到143组对应响应值，如表5所示。

表5 因素与响应试验数据

对表(5)中的试验数据进行多元二次回归拟合，得到SRG转矩脉动KTr、发电机效率η、功率密度ρm响应面模型的函数表达式(3)～(5)：(SRG响应面模型的具体表达式见附录)

KTr(x)=fKTr(x1,x2,x3,x4,x5,x6,x7)

(3)

η(x)=fη(x1,x2,x3,x4,x5,x6,x7)

(4)

ρm(x)=fρm(x1,x2,x3,x4,x5,x6,x7)

(5)

SRG优化目标响应面模型回归分析如表6所示。

表6 SRG优化目标响应面模型回归分析表

有效信号与噪声比值Adeq.Precision>4，变异系数C.V.%<10，响应面模型有较高的可信度和精确度；P值(Model Prob>F)均小于0.01，响应面模型显著，拟合度好，具有高度统计学意义；多元相关系数R2及校正系数Adj.R2均大于0.9，各响应面模型预测准确度较高。因此，构造的SRG优化目标响应面模型拟合度好，可信度与精度较高。

3.3 NSGA-Ⅲ优化算法

NSGA-Ⅲ预定义一组与种群数量相近的参考点，将种群数量为N的第t代父代种群Pt与经过交叉、变异生成的子代种群Qt合并，对种群数量为2N的合并种群Rt=Pt∪Qt进行基于参考点的非支配排序以及参考点与种群个体的关联操作，筛选出新的种群数量为N的集合St为新的父代种群。

NSGA-Ⅲ优化算法的主要操作：

(1)参考点的选取：

本文采用Deb and Jain方法生成内、外两层参考点，不仅减少参考点数目，而且保证了参考点的广泛分布[14,17]。外层参考点由Das and Dennis方法生成，结合式(6)～式(8)得到外层参考点集S1：

(6)

(7)

(8)

基于外层参考点，由式(9)得到内层参考点集S2：

(9)

则(M-1)维超平面上预定义的参考Rt=Pt∪Qt点集为S=S1∪S2。

(2)理想点初始化：

(10)

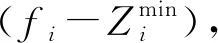
(3)基于关联操作的精英选择机制：

(11)

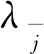
重复K次直到满足种群Pt+1的个体数为N。

NSGA-Ⅲ优化算法的流程图如图2所示。

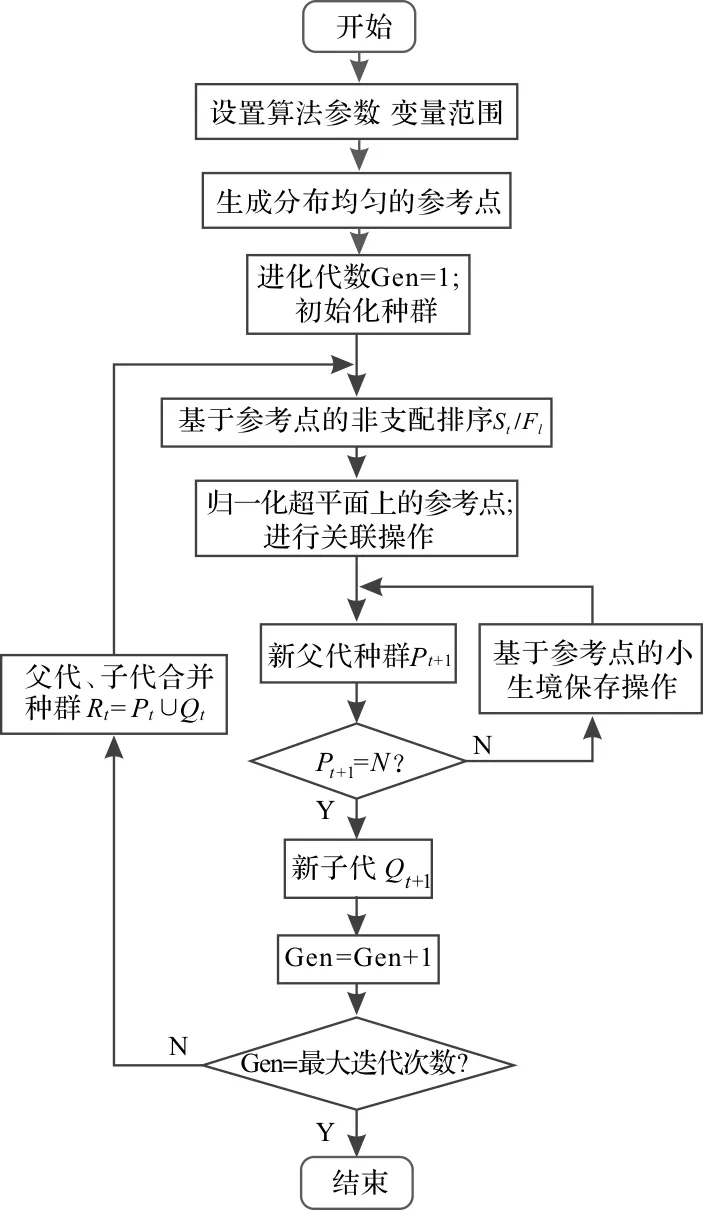
图2 NSGA-Ⅲ优化算法流程图

4 优化与仿真分析

利用NSGA-Ⅲ对1kW四相8/6极SRG的转矩脉动、效率及功率密度响应面模型进行多目标优化，设置种群规模N=200，交叉分布参数ηc=30，变异分布参数ηm=20，最大迭代次数GMax=500。得到如图3所示Pareto前沿。

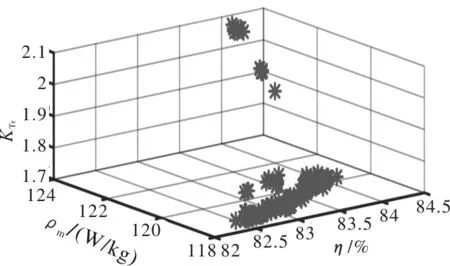
图3 Pareto前沿

图中Pareto解集中所有解的约束违反度为0，均为满足SRG性能约束的可行解。SRG优化后的模型应满足：KTr<2.0619，η>80.54%，ρm>117.2574 W/kg，在三维空间不易看出各优化目标间的制约关系，将三维视图转换为二维视图对两两优化目标间的制约关系进行分析，得到如图4所示优化目标约束后的可行解二维剖面图。

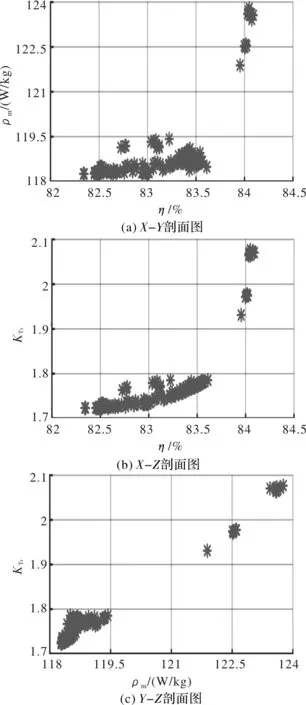
图4 Pareto前沿剖面图

由图4二维剖面图可行解的分布分析得到SRG转矩脉动与发电机效率、功率密度相互制约：转矩脉动与发电机效率、功率密度呈现正相关趋势。决策者可依据偏好选取最优解，在图4(b)SRG功率密度约束下，取7组不同效率下的SRG可行解验证优化效果，7组解的分布如图5所示。

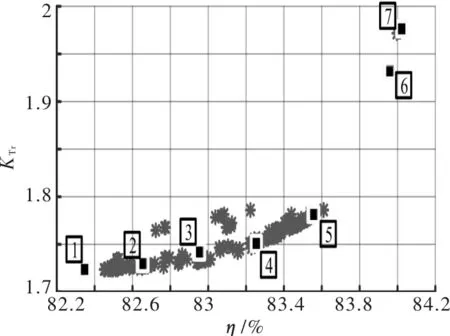
图5 约束后的Pareto可行解分布

图5的7组优化方案中，方案1转矩脉动最小，方案7功率密度、发电效率最大。表7、表8对其优化结果进行分析。(表7中的θon和θc均为电角度)

表7 基于NSGA-Ⅲ的SRG优化方案

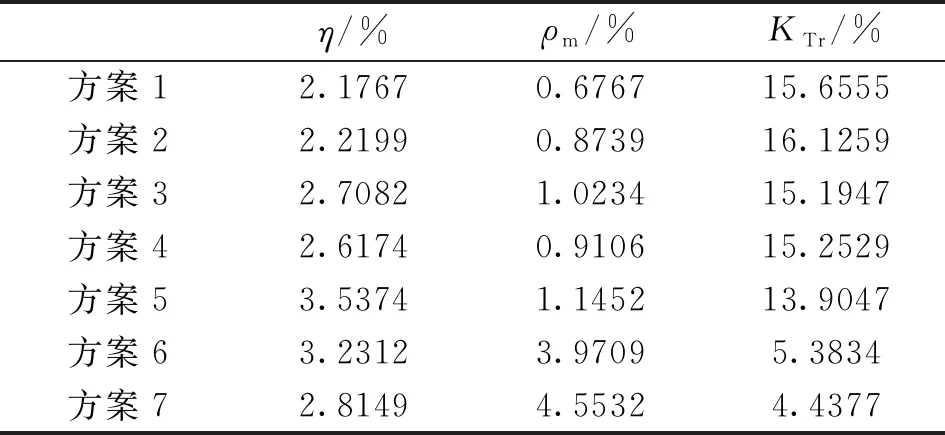
表8 SRG优化方案的结果分析

表7列出的7组优化方案的参数组合从不同程度上优化了SRG三个目标函数，给出了SRG的多目标优化解。利用有限元仿真对7组方案进行有限元分析，通过相对误差分析验证其准确性，如表9所示。

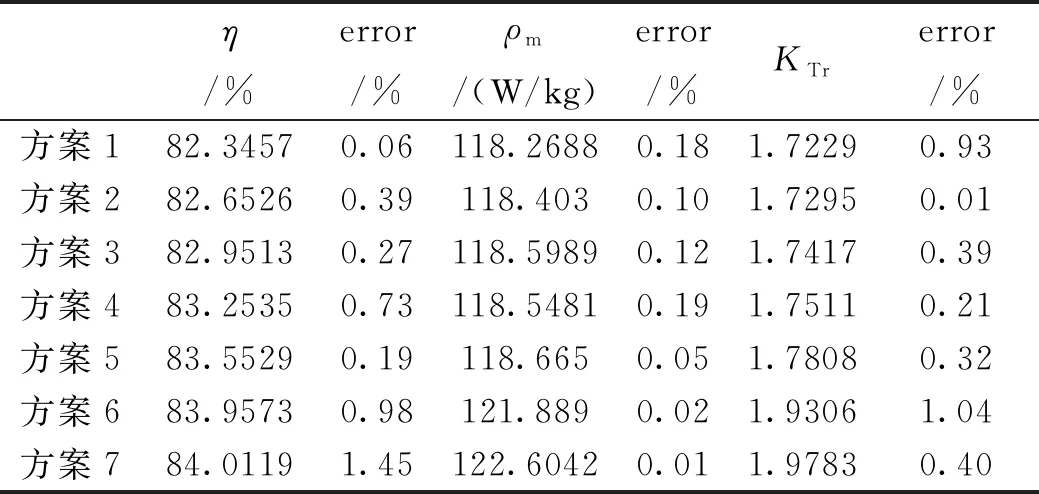
表9 基于NSGA-Ⅲ的SRG优化方案误差分析

表9中，通过7组方案中的SRG响应面模型与有限元模型的误差分析数据表明，响应面模型相对误差均小于1.5%，可见，SRG响应面模型优化精确度较高。

5 结 论

本文主要进行了SRG结构参数与控制参数的多目标优化设计方法研究。建立以转矩脉动、效率、功率密度为优化目标的SRG多目标优化模型，通过对优化目标的参数化分析确定优化变量。利用RSM方法建立SRG优化目标函数的回归模型，采用NSGA-Ⅲ优化算法进行最优化解算。通过仿真分析并对比了SRG优化前后的发电机运行性能，所选取7组Pareto可行解的优化方案均能在减小SRG转矩脉动的同时，提高发电机整体运行效率及功率密度，有效地改善了SRG的运行性能，最后通过有限元仿真验证了SRG回归模型的准确性。