基于海量序列数据的公交用户群体出行预测研究

冯 路，钱 宇，白梦娜，袁 华

基于海量序列数据的公交用户群体出行预测研究

冯 路，钱 宇*，白梦娜，袁 华

（电子科技大学 经济与管理学院，四川 成都 611731）

在海量序列数据中，预测群体用户在未来一段时间中的可能行为模式是一个非常有意义且具有挑战性的研究问题。本文以公交用户群体出行为例，通过引入相空间重构法，利用海量序列数据对大型系统建立模型来模拟其动态演化模式。同时，考虑到一般相空间预测方法在大数据情况下的不足，提出了相似性拐点方法进行预测前的相似点的自动挑选工作，该方法不但降低了预测过程中的相似度计算复杂度，同时也显著提升了预测效果。实验证明，本文的方法对于探讨利用海量（周期性）序列数据进行系统建模，以及预测一段时间内的群体行为提出了新的思路。

海量序列数据；相空间重构；相似性；预测

0 引言

公共交通是我国城市居民出行的重要交通方式，实现对公交用户群体出行行为的准确预测，对于提升公共资源使用效率[1]，优化城市公共交通的管理，促进城市计算智慧化具有重要意义[2]。

交通流相关的预测研究经历了很长时间的发展。最常用的研究方法是直接探讨交通流数据中的数据变量相关性，即各种参数（回归）方法。简单的如历史平均法和各种（非）线性回归模型[3]。这类方法操作简单且计算方便，但是预测精度较低。因此，进一步的研究中开始重视数据的时序相关性，进而形成了目前最成熟的时序预测方法――自回归移动平均模型（ARMA/ARIMA），它的各种模型在交通预测领域有着广泛的应用[4,5,6]。但是该类模型需要比较平稳的序列数据，抗干扰和波动性差。为了提高模型的稳定性和预测精度，一些考虑参数的智能方法，如Kalman滤波[7]、支持向量机（SVM）[8,9]、贝叶斯网络[10]、神经网络[11-13]以及它们的组合[10,14]方法等都被应用到研究中。这类方法的预测精度虽然很高，但是通常会面临复杂的数据及特征选择问题[15,16]。神经网络虽然很适合模拟数据的非线性关系，但模型训练过程收敛速度较慢，容易陷入局部最优。随着研究的不断深入，人们逐渐认识到以往的方法多是基于对系统基本结构的假设来进行对系统的预测，而城市交通是一个非常复杂的巨型系统[17]。因此，有研究分别从多因素、非参数方法和非线性系统的角度来分析预测交通流。多因素的研究认为，公交客流不仅受到用户自身的影响，还受到诸如经济状况、天气等多因素的影响[13]。非参数（回归）方法研究不需要任何先验知识，在有特殊情况时预测更有效[18-20]，能反映交通数据本身的非线性特征[20]。而非线性系统则引入非线性和系统动力学的方法对交通流动态及混沌特性进行识别，进而为短时交通流在小数据量上的预测提供基础[17,21]。

前述研究的共同问题是仅仅只针对短时交通流量的预测进行研究，而较长时间交通流的合理预测则能更好地为交通管理提供服务[22]。但是，传统方法在处理长时间预测任务时，由于观察（数据）的局限，容易陷入过渡预测（Over Prediction）的情况[23]。随着智慧交通的出现，人们期望利用公交大数据对较长时间的用户群体出行行为实现精准预测。然而，传统建模预测方法在大数据环境下面临着技术挑战[24]：一是系统复杂度高，内部成分（如用户）多样，应用场景也不尽相同，很难从中提取出具有代表性的用户行为；二是系统快速演变，这使得基于样本的模型很快就不能反映系统当前的情况。此外，在大数据下对复杂系统建模而不考虑混沌特征可能导致不可预期的结果[25]。因此，我们需要一个基于海量数据驱动且更稳定的建模方案来实现对公交出行系统的历史状态描述和未来状态预测功能。

城市公交是一个复杂的非线性系统[17,20]，积累了海量用户出行数据。为了对其建立稳定的数据驱动的系统模型并实现较长时间的系统状态预测，本研究将首先引入相空间重构法[26]来描述海量公交群体行为产生的数据序列的性质和规律。相空间重构是数据驱动的建模方法[27]，它以Takens嵌入定理[28]为基础，具有很好的数学性质。由于能够较好地捕捉时间序列的动态等价性，它被广泛应用于复杂系统特征描述和状态预测[17,21,29]。然后，本文提出了一种新的方法来预测目标点的下一状态。为此，作者先计算出目标点在相空间中尽量多的相似点集合。接着，利用目标点与其相似点之间的相似性变化拐点，从大量相似点里自动挑选“最相似”的点集合。最后，通过拟合这些“最相似”点与其临近下一状态点的关系来实现预测。实验结果表明，本文提出的新方法在大数据环境下，能够同时达到避免过渡预测和提高预测精度的目的。

1 延迟坐标相空间重构

1.1 问题定义

混沌时间序列重构相空间的工作始于Packard等人的研究[26]，他们提出了重构相空间的两种方法：导数重构法和延迟坐标重构法。鉴于数值微分的计算过程对误差很敏感，普遍采用的是以Takens嵌入定理为基础的延迟坐标相空间重构法。该方法利用时序系统某一状态变量() 的延迟变量(+) 来构造一个维的状态向量，即：

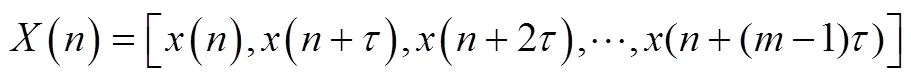
这样，从一维混沌时间序列中可以重构一个与其原动力系统在拓扑意义下等价的相空间。() 即是相空间中的点。实际应用中，如果对延迟时间和嵌入维数作出合理选择，那么我们能够在重构的相空间中将反映时间序列特征规律的轨迹恢复出来，并构造一个反应邻近序列关系的映射来实现预测：

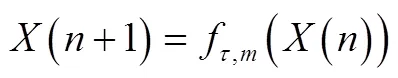
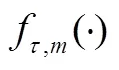
1.2 延迟时间τ的确定

确定延迟时间的方法主要有互信息法[30,31]和自相关函数法[32]。互信息法是通过计算时间序列的互信息值，并寻找到互信息第一个极小值所对应的时间延迟作为重构相空间的延迟时间。互信息法并不能保证互信息总存在极小值，即使存在，也有可能是系统的震荡引起的，而且计算互信息也相对较复杂。自相关函数法，是通过计算自相关函数来确定延迟时间，自相关函数的定义为：

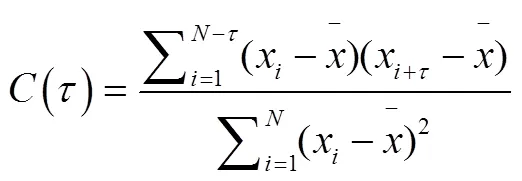
1.3 嵌入维数m的确定

根据Takens嵌入定理[28]，嵌入维数应满足≥ 22+1，这里2为吸引子的关联维数。关联维数是判别吸引子类型以及复杂程度的表征量，它可以描述系统在整个变化中稳定性和确定性的程度。显然，如果关联维数2确定，则嵌入维数的范围也随之确定。本文采用的是由Grassberger和Procaccis提出的G-P算法[33]来估计关联维数2。

在确定的情况下，考察维重构相空间中的两个不同点：

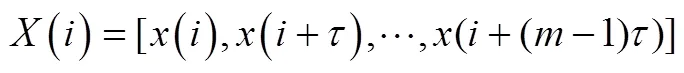
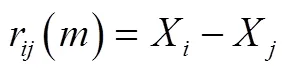
给定一个距离阈值，计算所有距离小于的“相点对”数占全部“相点对”数的比例，即

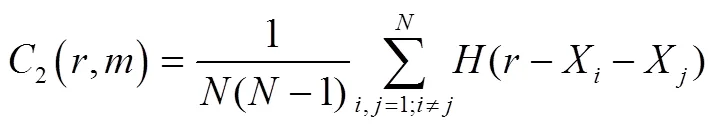
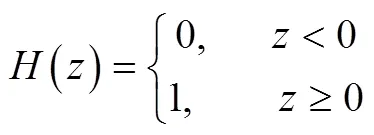
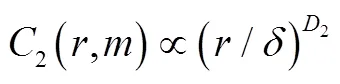
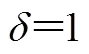
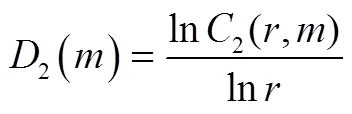
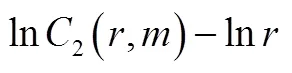
2 基于重构相空间的预测方法

显然，在局部预测算法中选择一个合适的值非常重要。然而，在大数据环境下选择也将面临困境：如果选取的较小，则参与预测的历史点很少，模型容易受到噪音点很大的影响或者对那些与当前点非常相似点产生过拟合；反之，如果选取的较大（这也是在大数据环境下的通常做法），参与预测的历史点很多，此时固定的个点与() 相似性变化会变得剧烈。而且，随着预测的任务从传统的预测一个点的值提升到需要预测一段时间的值，则对于每一轮（不同的）预测任务选定的个相似点中与() 真正相似的点的个数并不相同。这样，如果预测过程中一直选取一样的值，那么预测结果将会有很大误差。为了获得() 的真正相似点的集合，在值较大的情况下，我们提出一个基于相似性拐点的方法来剔出那些与() 不太相似的点。假设获得的拐点位置为1 ≤≤，显然只有相似性关系排在前的相似点才与() 最相似。这样，在减少计算的过程中还可以提高预测精度。

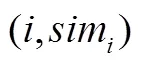
表1 相似性拐点算法

表2 基于相空间重构的预测算法

获得() 的个最相似点及相似性关系的拐点位置之后，则可以获得个相似状态点及其各自对应的个下一状态点。通过考察这2个点之间的一一对应关系就可构建最合适的映射关系(·)。最终，可以利用(·) 来实施有效的预测。预测的计算过程见算法2（表2）。

给定训练集重构的相空间，预测算法首先获得() 的个最相似点(Line 3-5)；然后调用算法1获得相似性关系的拐点位置(Line 6-7)；最后，通过拟合这个() 的相似点来获得映射关系(·) (Line 8-12)。为了减少运算复杂度，本文采用简单线性回归的方法进行局部拟合：

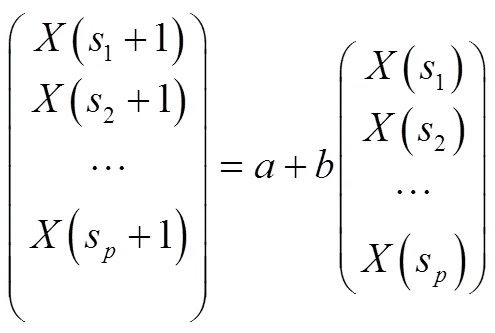
3 相空间生成实验

3.1 数据

实验数据为2014年8月1日至12月31日共5个月内广州市某公交线路的用户全部乘车记录。该公交线路每天运行时间为早上5:00 到晚上23:00，共18小时。以一张公交卡识别一个独立的用户（乘客），共有用户近162万人。用户乘车时需要刷卡一次，并且在系统中生成一条记录其消费行为的数据，共生成4,857,644条记录且以刷卡的顺序存储。原始数据集大小为2.12G。另外，考虑到用户在本线路乘车（刷卡）平均刷卡3 次，且刷卡频次呈长尾分布。且为了方便计算，剔除5个月里乘车次数不满10 次的乘客，剩下有效用户共78,704人，共有1,829,119 条乘车刷卡记录，平均23.2 次。

本研究的预测目标为：一段时间里，公交系统中每个工作小时的用户群体出行情况。为此，我们以小时为单位并将同一时间区间的所有乘车数据累计汇总。然后，取2014年12月8日之前的2,340小时（每天只考虑公交线路正常工作的18小时）的用户群体乘车情况作为训练集，之后的三周共378 小时作为预测的测试集。训练集中用户出行情况如图1所示。其中，横轴为2014年8月1日开始到2014年12月8日为止的工作小时序列，纵轴为对应的汇总乘车人次。此外，横轴200 附近的数据为缺失值，1000 附近的数据为国庆节数据。为了检验抗噪音特性，实验并未对缺失值和异常值进行特殊处理。而且，在4.4小节我们对刷卡次数较少的用户数据也进行了讨论。

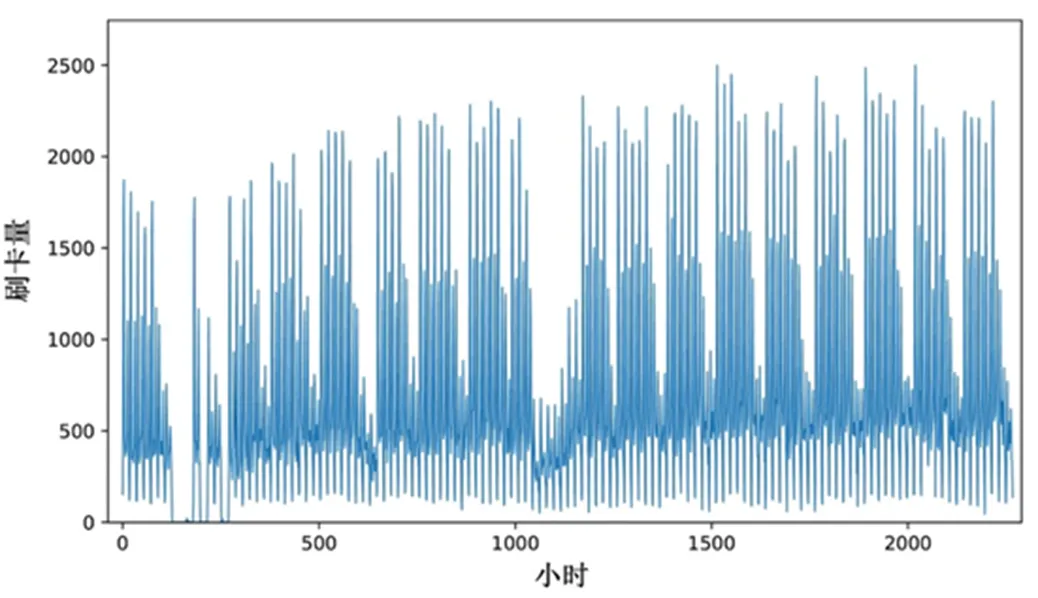
图1 训练数据集中用户的日常公交出行分布

Figure 1 Distribution of daily bus trips for users in the training data set

3.2 确定初始延迟时间

在确定初始延迟时间时，通常使用实际观测数据做出自相关函数随延迟时间变化的函数图像，然后观察图像的变化。将实验的训练数据以小时为单位分割后，当延迟时间取不同值时，自相关函数根据式(2)画出的图像如图2所示。其中可以发现看出，自相关函数衰减到经验值1时，附近可选的延迟时间值有= 1 和= 2。本文的后续实验中选取了最接近1的= 2 作为延迟时间。

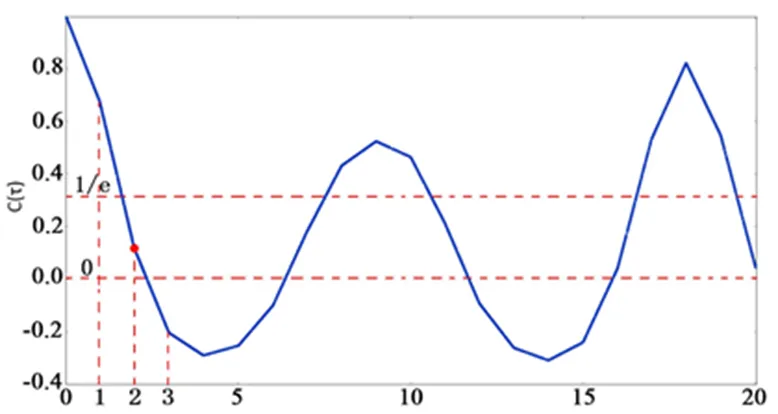
图2 自相关函数值图像

Figure 2 Image of autocorrelation function values

3.3 确定初始嵌入维数m

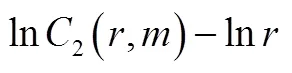
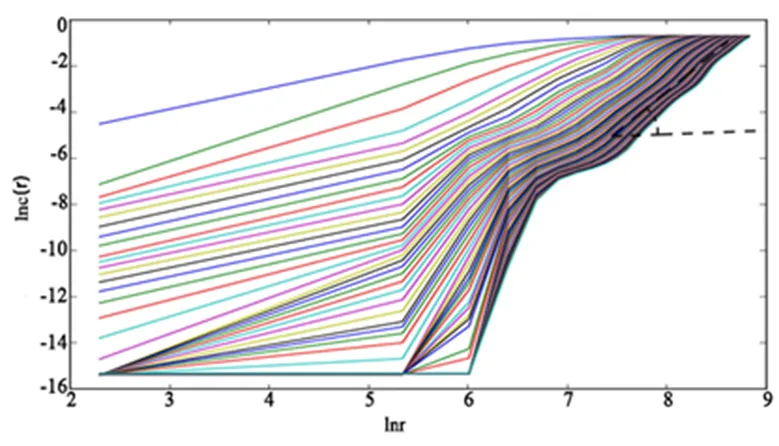
图3 关系曲线

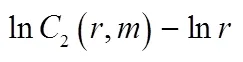
3.4 参数影响及相图变化趋势

前面的实验得出结论：最合适的延迟时间为2，嵌入维度大于等于5。为了印证这个结果是否合理，本文针对嵌入维数和延迟时间做了拓展实验。对于一个合理的相空间映射，在映射空间上，数据应该表现出明显的混沌吸引子，且各点取值应该偏多样化。基于此，我们需要根据前面计算得到的延迟时间值和嵌入维度范围，将公交出行数据（训练集）映射到高维相空间后进行相应的观察。由于嵌入维度太大，本文利用主成分分析法（PCA[34]）将相空间映射点降维到三维空间来可视化相图，从而观察实验结果。

当延迟时间= 2 保持不变，嵌入维数分别取5, 15, 25, 35, 45, 55 得到的相图如图4所示。从图4中的变化趋势可以看出：随着嵌入维数的变化，系统相图也在发生变化。总体上可以看出嵌入维数范围（= 5）则是相图趋于稳定的下界；随着嵌入维数的增加，相图逐渐趋近于平稳。这一实验结果说明了对相空间重构的影响：嵌入维数越大，相图就越趋于平稳。

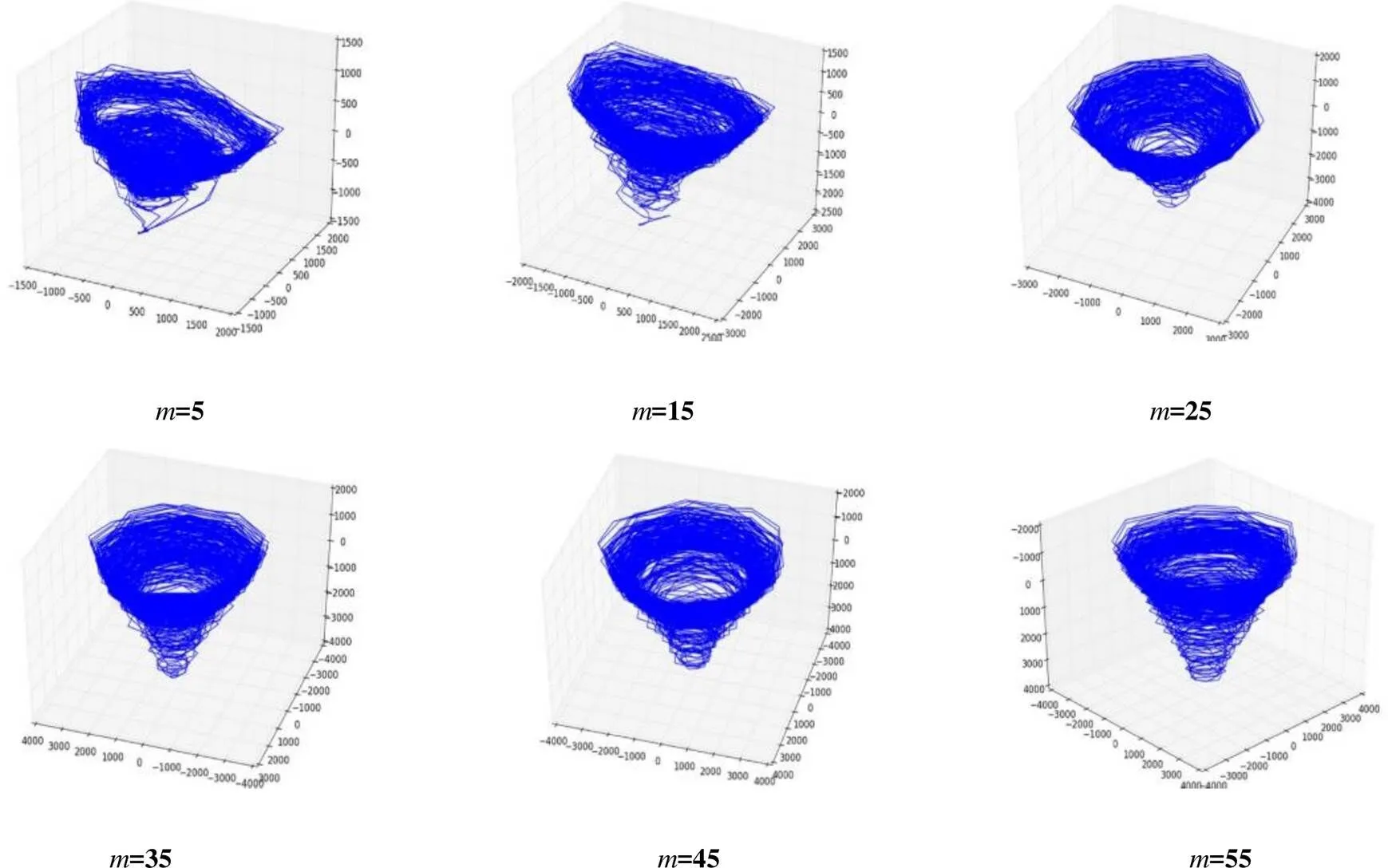
图4 不同嵌入维数m 得到的相图

Figure 4 Phase diagrams from different embedding dimensions m

在清楚了的影响前提下，我们可以选择一个较大的嵌入维数值（例如= 50），利用实验来观察延迟时间对相空间构建的影响。变化延迟时间从1 变到9，我们得到的相图如图5所示。可以从图5中的趋势看出：当延迟时间为= 2 时，所对应的相图最为稳定且吸引子状态更多样化；虽然= 1 所对应的相图也不错，但是稳定性和吸引子状态多样性都弱于= 2 的情况。这与图2的实验结果相吻合。然而当延迟时间分别为3, 5, 6, 7, 8 和9 时，相图虽然看上去很有规律，但没有表现出多态，只是在少数几个状态间跳跃变换。

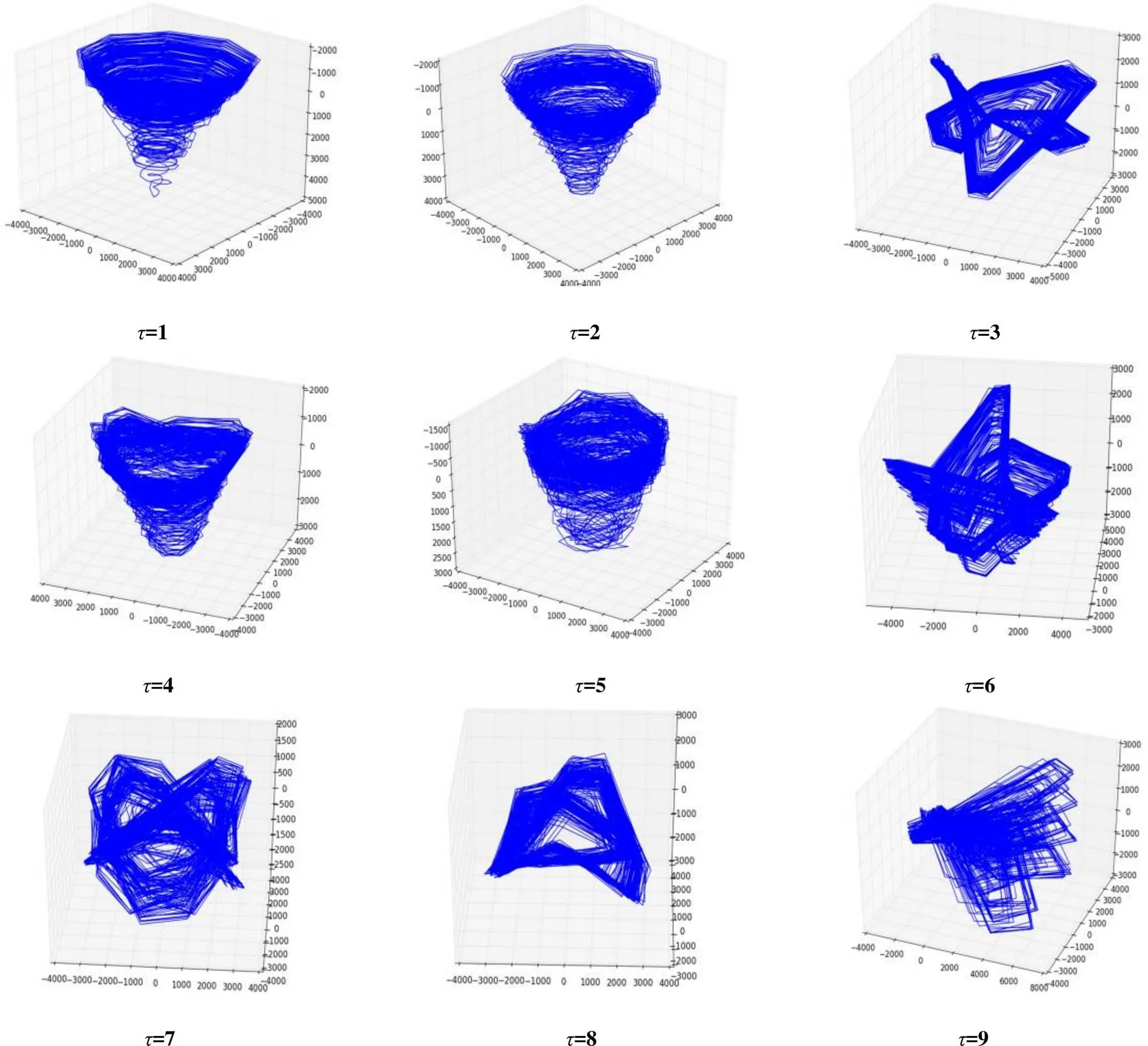
图5 不同延迟时间τ得到的相图

Figure 5 Phase diagrams from different delay times τ

4 用户群体出行预测实验

4.1 预测评价指标

对于提出的公交出行预测目标，本文采用两个评价指标为：平均绝对百分误差（MAPE）[35]和希尔不等系数（TIC）[36]。其定义分别如下：

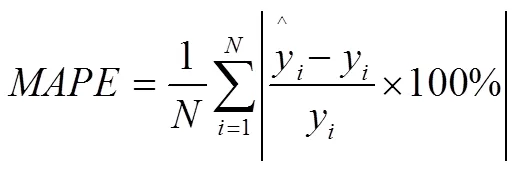
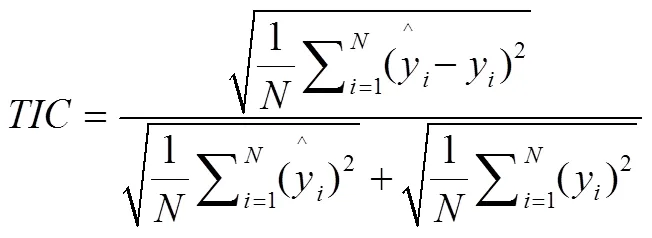
4.2 预测结果

传统的预测方法认为每一个目标点都具有相似的近似点数量，因此取的相似点数目完全一样，为固定值，这样的假设显然不合理。图6给出了四个需要预测的目标点与其最相似的= 20 个点的相似度变化曲线。图中红色的点为这20个点中与目标点相似性排序的拐点。如果设定0= 10，对于= 5 图中这类目标点与其相似点的相似度变化拐点0，因而需要在排序为到的相似点集合中继续计算相似性续拐点，直到找到的拐点排序大于0。对于= 16 类似的目标点，它们与相似点之间的相似度变化很均匀，如果不找拐点，对其影响不大。而对于= 13 和= 11图中的目标点，能明显找出一个相似度变化剧烈变化的地方。拐点之后的点虽然还在目标点相似度排序的前20 范围中，但是它们与目标点的相似度差已迅速增大。如果将这些通过固定值方法找到的所有点一视同仁，（尤其是值比较大时）将会导致拟合效果欠佳。

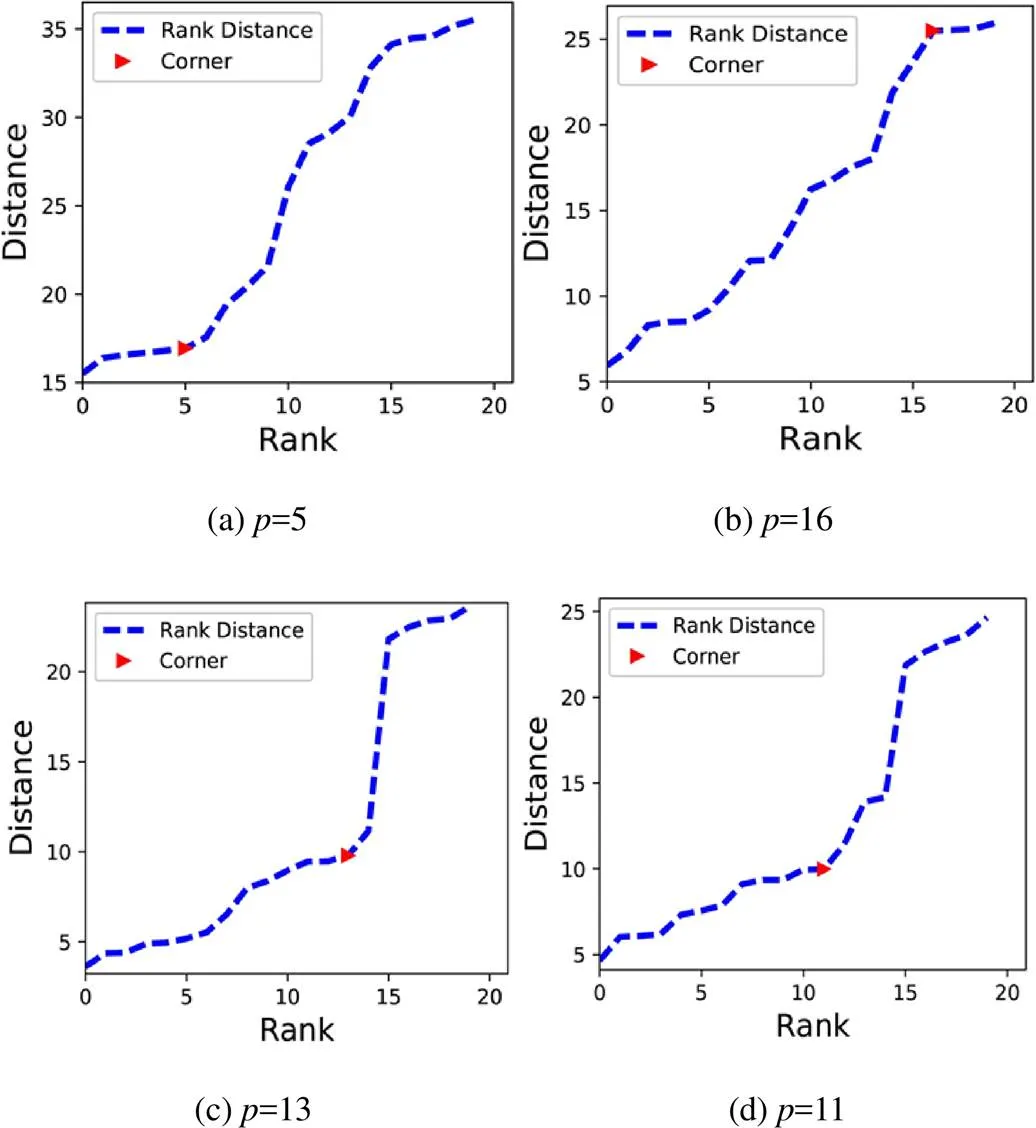
图6 部分目标点与相空间中20个最相似点的相似度变化曲线示例

Figure 6 Examples of similarity curve between some target points and the 20 most similar points in phase space

在一个值比较大的相似点集合中，将拐点之前的点看作是目标点的“最相似”点集，本文提出了一个实现更准确预测的新思路：找到足够多的，且与目标点“最相似”的历史状态点，进而通过拟合这些“最相似”点与各自下一时刻点之间的关系对系统下一状态的进行预测。为了说明这一方法的优势，表3为当延迟时间为= 2，嵌入维数为41到60时，本文的方法和传统固定值（= 20）方法的MAPE和TIC指标具体变化情况对比（其中*表示用找相似性拐点的方法的预测结果）。可以看出，本文提出的找拐点的方法，不仅MAPE 值有相当可观的下降（约10%），而且TIC值也有很大程度的降低，且稳定时TIC值小于0.1，这表明拟合效果很好。

进一步，我们选择表3中预测效果最好的实验参数（延迟时间为2，嵌入维数为53），本文方法在测试的三周共378 小时上的预测值与真实值的匹配结果如图7所示（其中蓝线为真实值，红线为预测值）。

为了更清晰地展现实验效果，我们从图7的全部时间中选出四个时间片段（即0-30小时，100-130小时，200-230小时，300-330小时）的实验情况进行放大展示，结果如图8所示。图中的蓝线（实线）表示真实发生的刷卡数据，红线（虚线）表示本文方法的预测结果。实验结果表明，本文方法的预测结果能够很好地拟合公交用户真实的刷卡行为。

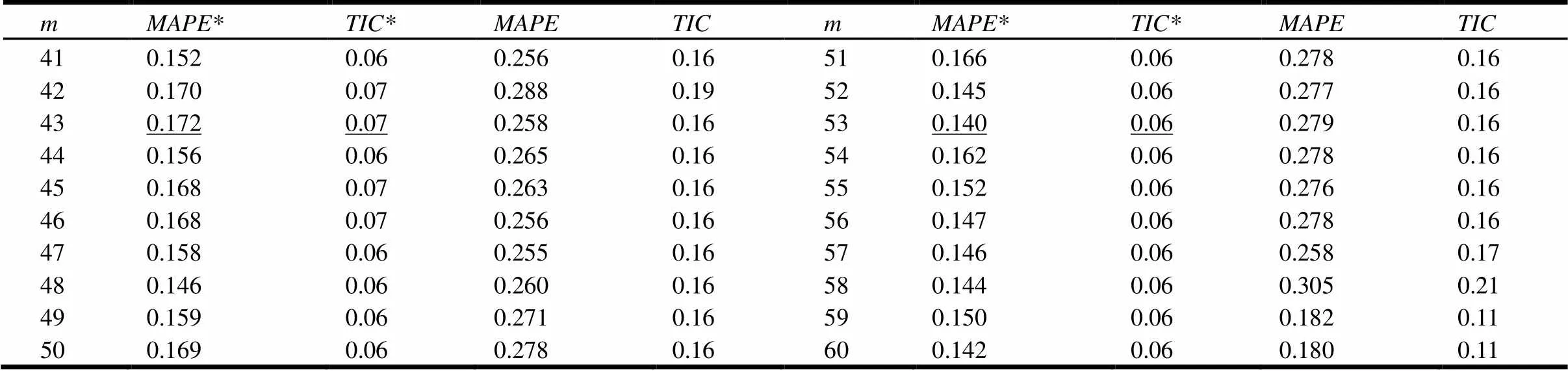
表3 新方法与固定值方法（k = 20）预测结果的MAPE和TIC变化情况对比

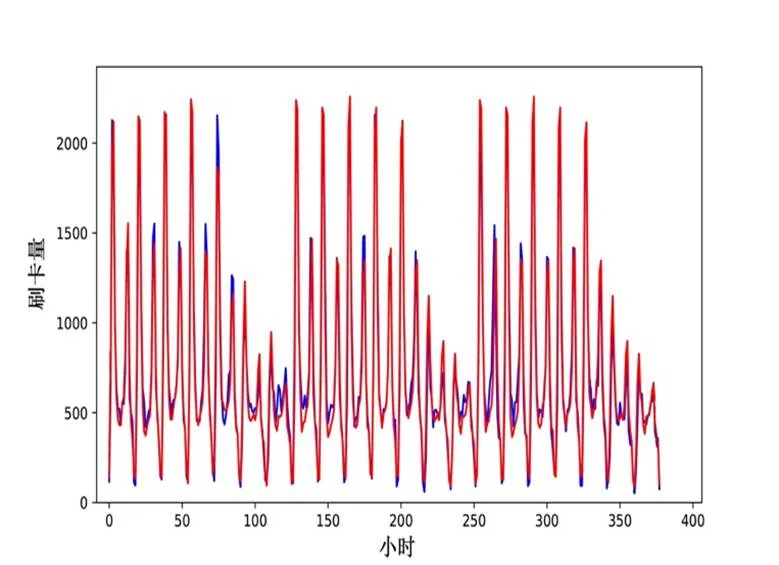
图7 预测值与真实值的匹配结果示意（τ = 2, m = 53）

Figure 7 The matching result between the predicted value and the real value（= 2,= 53）

4.3 对比实验

本文的方法与时间序列预测研究中常用的“ARMA模型”和“对应位置回归”（Cor Reg）[19]两种方法进行了对比实验。ARMA模型是最常用的平稳时间序列拟合模型。对应位置回归方法认为系统的周期中具有相关性的时间点在状态上也应该相关。因此需要一定先验知识来确定周期（延迟时间），以及在一系列相关的状态集合上，再运用回归（如非参数K-NN）进行相关性拟合来实现预测。例如，若要预测某个星期一早上8点的公交流量，则在数据集中去寻找所有星期一早上7点的数据，并回归拟合这些数据与其下一时刻（星期一早上8点）的关系。这里需要先验地确定时间延迟为7天（一周），并找到预测目标（星期一早上8点）的相关状态集合（所有星期一早上7点）。

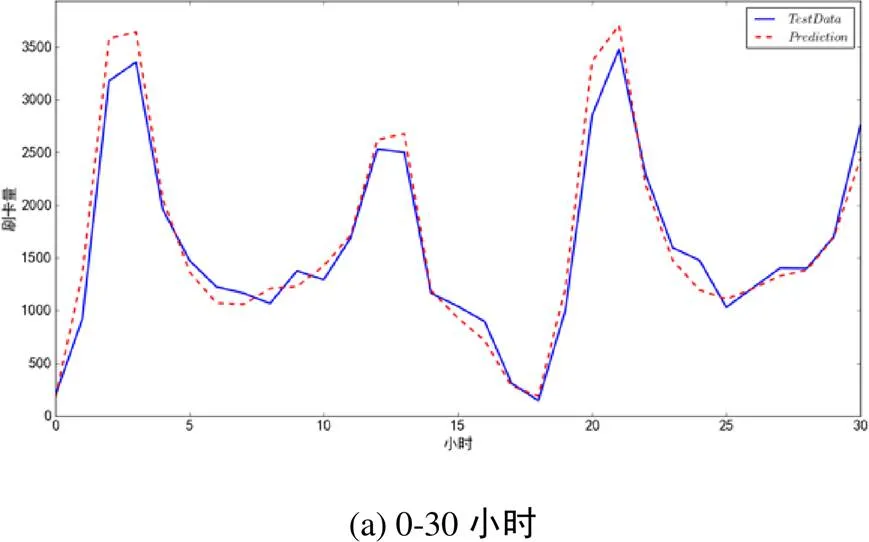
图8 预测值与真实值在四个时间片段上的放大显示效果

Figure 8 Enlarged display effect of predicted value and real value in four time segments

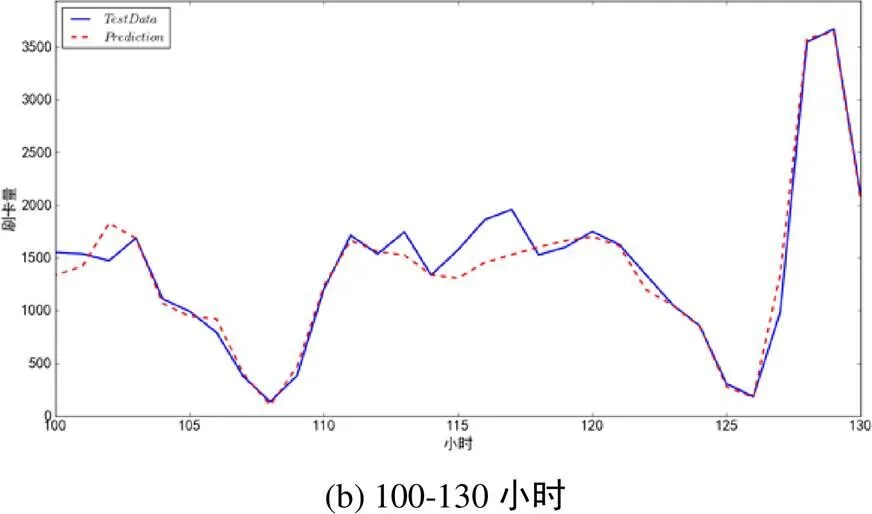
图8（续） 预测值与真实值在四个时间片段上的放大显示效果

Figure 8(continue) Enlarged display effect of predicted value and real value in four time segments

表4为在公交大数据集上，三种预测方法的MAPE值和TIC值。本文提出的新方法无论是MAPE值还是TIC值都优于其他两种方法。值得一提的是，对于Cor Reg方法，其MAPE值和TIC值虽然与本文提出的方法很接近，但是此方法基于很强的先验知识，在实际应用中，很可能因为数据缺失或异常值导致预测结果很不稳定。

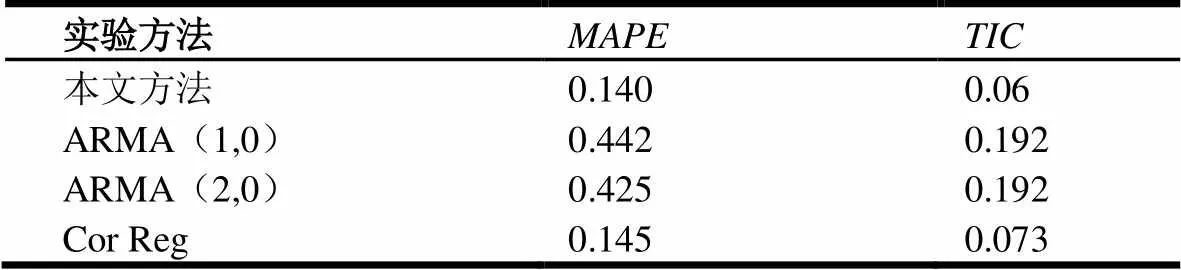
表4 对比实验结果

4.4 讨论

在前述实验中的数据中，我们剔除了5个月时间里乘车次数不满10 次的乘客，用剩余部分38%的数据对乘客的公交出行行为进行预测。但是我们进一步发现，乘车次数不满10 次的这类乘客虽然人均刷卡次数较少，但是人数众多且占到近62%的刷卡记录。显然，被剔除的乘客乘车次数虽少但数量巨大，也应当作为被预测的群体之一。

本部分的实验工作，用于讨论分析本文方法对于噪音数据的处理能力。本文将乘车“刷卡次数”作为变量进行考虑。分别以“刷卡次数”= 1次，= 2次，…，直到= 15次分别作为不同的依据进行数据划分。即每次实验中我们把“刷卡次数”大于等于次的作为一部分实验数据；同时将对应的“刷卡次数”小于次的作为另一部分实验数据。这样我们可以获得15对的数据集，可以用来检验在不同噪音水平下本文方法的预测效果。检验的指标仍然采用MAPE值和TIC值，实验结果见图9。

图9中蓝色实线表示“刷卡次数”小于数据集的预测结果（图中用标识），红色虚线表示“刷卡次数”大于数据集的预测结果（图中用标识）。首先，随刷卡次数的增加，图中的红色虚线均低于蓝色实线。这表明刷卡次数多的用户比刷卡次数少的用户表现出更强的出行规律性。其次，图中的蓝色实线呈逐步下降趋势，意味着本文预测方法的准确度在不断提高。即随着刷卡次数的增多，用户乘坐公交车的规律性也在不断增强。最后，图中的红色虚线存在缓慢上升趋势，表明那些刷卡次数非常多的用户，其乘车非规律性的出行行为也在随之增加，本文预测方法的准确度将会受到一定影响。

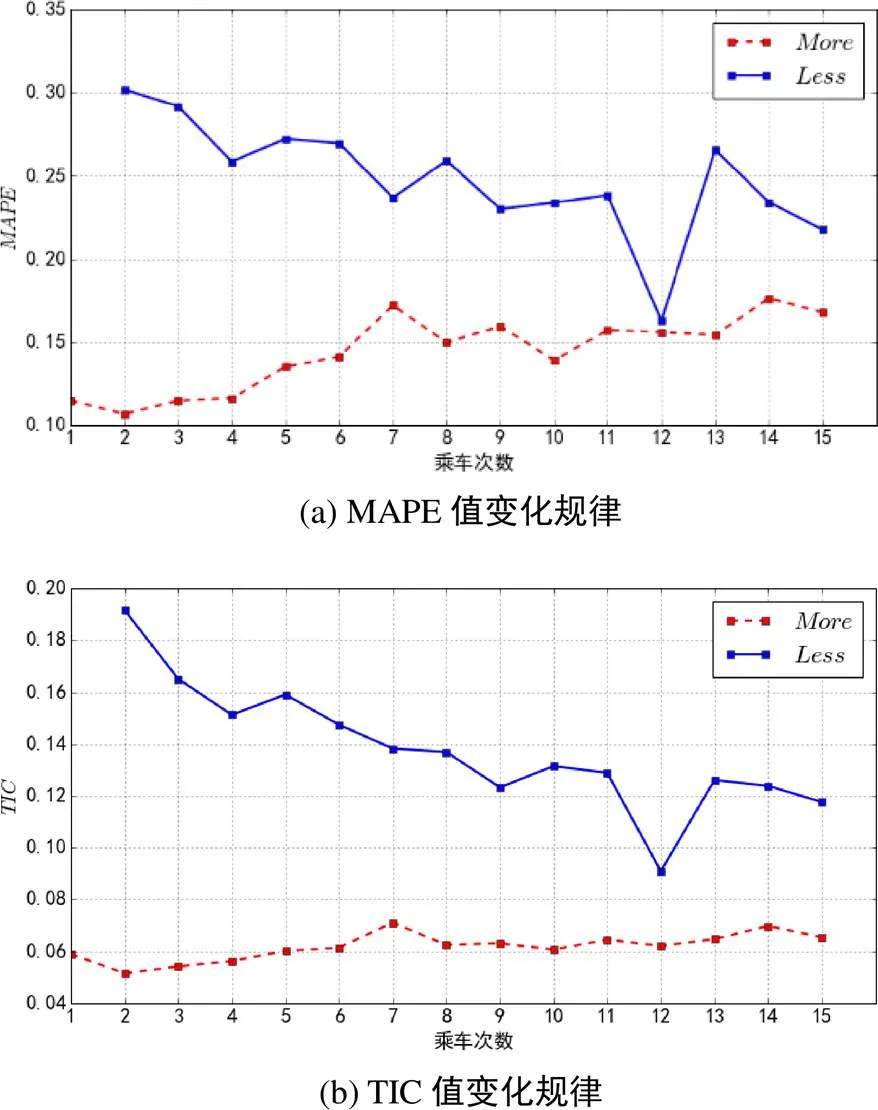
图9 剔除不同“噪音”数据的预测结果变化实验

Figure 9 Experiments of changing prediction results by excluding different “noise” data

5 结论

公交系统实现智能化的关键是对公交客流的全面、准确把握和预测。公交客流的刷卡行为可以生成海量序列数据，因而如何利用这些海量序列数据，来提高对群体用户在未来一段时间中的可能行为的预测效率是一个非常有意义的研究问题。但是，传统的建模预测思路在大数据环境下会面临模型数据选择的合理性和长期预测的准确性挑战。

本文引入相空间重构的方法研究了海量序列数据的系统建模，让更多的系统数据参与到模型构建过程中来。此外，为了获得更准确的预测结果，本文通过先构建一个较大的相似点集合，并在此基础上通过寻找拐点的方法，无监督地根据目标点的不同进而选择不同的（最）近似点数量，以至于对预测模型结果进行优化。该方法不但降低了预测过程中的相似度计算复杂度，同时也显著提升了预测效果。实验证明，本文提出的方法对于利用复杂系统的海量（序列）观察数据进行系统建模，以及基于模型预测较长一段时间的群体行为模式提供了新的思路和方法。

[1] 杨浩雄, 李金丹, 张浩, 刘淑芹. 基于系统动力学的城市交通拥堵治理问题研究[J]. 系统工程理论实践, 2014, 34(8): 2135-2143.

Yang H X, Li J D, Zhang H, Liu S Q. Research on the governance of urban traffic jam based on system dynamics[J].Systems Engineering-Theory & Practice, 2014, 34(8): 2135-2143.

[2] Yu Zheng, Licia Capra, Ouri Wolfson, Yang Hai. Urban Computing: Concepts, Methodologies, and Applications[J]. ACM Transaction on Intelligent Systems and Technology, 2014, 5(3), 38:1-55.

[3] Liang Dai, Wen Qin, Hongke Xu, et al. Urban traffic flow prediction: A MapReduce based parallel multivariate linear regression approach[C]. In Proceedings of the 17th International IEEE Conference on Intelligent Transportation Systems, 2014: 2823-2827.

[4] M. Gong, X. Fei, Z. H. Wang, et al. Sequential framework for short-term passenger flow prediction at bus stop[J], Journal of the Transportation Research Board, 2014, vol. 2417: 58–66.

[5] 朱广宇, 王雨晨, 张彭等. 基于变点发掘的城市轨道交通客流预测模型[J]. 中南大学学报(自然科学版), 2016, 47(6): 2153-2159.

Zhu G Y, Wang Y C, Zhang P. A forecasting model for urban rail transit passenger flow based on change-point detection method[J]. Journal of Central South University (Science and Technology), 2016, 47(6): 2153-2159.

[6] 梁昌勇, 马银超, 陈荣等. 基于SVR-ARMA组合模型的日旅游需求预测[J]. 管理工程学报, 2015, (1):122-127.

Liang C Y, Ma Y C, Chen R. The Daily Forecasting Tourism Demand Based on SVR-ARMA Combination Model[J]. Journal of Industrial Engineering and Engineering Management, 2015, (1):122-127.

[7] 张春辉, 宋瑞, 孙杨. 基于卡尔曼滤波的公交站点短时客流预测[J]. 交通运输系统工程与信息, 2011, 11(4): 154-159.

Zhang C H, Song R, Sun Y. Kalman Filter-Based Short-Term Passenger Flow Forecasting on Bus Stop[J]. Journal of Transportation Systems Engineering and Information Technology, 2011, 11(4): 154-159.

[8] 袁健, 李茂同, 范炳全. 短时交通流预测FSMSVR模型[J]. 系统工程与理论实践, 2014, 34(6): 1607-1613.

Yuan J, Li M T, Fan B Q. A FSMSVR model of short-term traffic forecasting[J]. Systems Engineering-Theory & Practice, 2014, 34(6): 1607-1613.

[9] Yuxing Sun, Biao Leng, Wei Guan. A novel wavelet-SVM short-time passenger flow prediction in Beijing subway system[J], Neurocomputing, 2015, Volume 166: 109-121.

[10] 王建, 邓卫, 赵金宝. 基于贝叶斯网络多方法组合的短时交通流量预测[J]. 交通运输系统工程与信息, 2011, 11(4): 147-153.

Wang J, Deng W, Zhao J B. Short-Term Freeway Traffic Flow Prediction Based on Multiple Methods with Bayesian Network[J]. Journal of Transportation Systems Engineering and Information Technology, 2011, 11(4): 147-153.

[11] Wei Y, Chen M C. Forecasting the short-term metro passenger flow with empirical mode decomposition and neural networks[J]. Transportation Research Part C: Emerging Technologies, 2012, 21(1): 148–162.

[12] Zhao S Z, Ni T H, Wang Y, et al. A new approach to the prediction of passenger flow in a transit system[J], Computers & Mathematics with Applications, 2011, 61(8): 1968-1974.

[13] Y. Mo, Y. Su. Neural networks based real-time transit passenger volume prediction[C]. In Proceedings of the 2nd International Conference on Power Electronics and Intelligent Transportation System (PEITS), 2009, pp. 303-306.

[14] 沈国江, 王啸虎, 孔祥杰. 短时交通流量智能组合预测模型及应用[J]. 系统工程理论实践, 2011, 31(3): 561-568.

Shen G J, Wang X H, Kong X J. Short-term traffic volume intelligent hybrid forecasting model and its application[J]. Systems Engineering-Theory & Practice, 2011, 31(3): 561-568.

[15] Isabelle Guyon, Andr´e Elisseeff. An Introduction to variable and feature selection[J]. Journal of Machine Learning Research, 2003, 3:1157-1182.

[16] JoséA. S´aez, J. Luengo, F. Herrera. Predicting Noise Filtering Efficacy with Data Complexity Measures for Nearest Neighbor Classification[J]. Pattern Recognition, 2013, 46(1): 355-364.

[17] 董超俊, 刘智勇, 邱祖廉. 基于混沌理论的交通量实时预测[J]. 信息与控制, 2004, 33(5):518-522.

Dong C J, Liu Z Y, Qiu Z L. Prediction of Traffic Flow in Real-time Based on Chaos Theory[J].Information and Control, 2004, 33(5):518-522.

[18] 张晓利, 贺国光, 陆化普. 基于K-邻域非参数回归短时交通流预测方法[J]. 系统工程学报, 2009, 24(2):178-183.

Zhang X L, He G G, Lu H P. Short-term traffic flow forecasting based on K-nearest neighbors non-parametric regression[J]. Journal of Systems Engineering, 2009, 24(2):178-183.

[19] 张晓利, 陆化普. 非参数回归方法在短时交通流预测中的应用[J]. 清华大学学报(自然科学版), 2009, 49(9):39-43.

Zhang X L, Lu H P. Non-parametric regression and application for short-term traffic flow forecasting[J]. Journal of Tsinghua University (Science and Technology), 2009, 49(9):39-43.

[20] 张涛, 陈先, 谢美萍等. 基于K近邻非参数回归的短时交通流预测方法[J]. 系统工程理论实践, 2010, 30(2): 376-384.

Zhang T, Chen X, Xie M P,. K-NN based nonparametric regression method for short-term traffic flow forecasting[J]. Systems Engineering-Theory & Practice, 2010, 30(2): 376-384.

[21] 张洪宾, 孙小端, 贺玉龙. 短时交通流复杂动力学特性分析及预测[J]. 物理学报, 2014, 63(4): 55-62.

Zhang H B, Sun X D, He Y L. Analysis and prediction of complex dynamical characteristics of short-term traffic flow[J]. Acta Physica Sinica, 2014, 63(4): 55-62.

[22] 周浩, 胡坚明, 张毅等. 基于隐Markov模型的短时交通崩溃事件预测[J]. 清华大学学报(自然科学版), 2016, 56(12): 1333-1340.

Zhou H, Hu J M, Zhang Y,. Short-term traffic breakdown prediction using a hidden Markov model[J]. Journal of Tsinghua University (Science and Technology), 2016, 56(12): 1333-1340.

[23] Kenneth Button. Transport safety and traffic forecasting: An economist’s perspective[J], IATSS Research, 2014, 38(1):27-31.

[24] 孟小峰, 慈祥. 大数据管理：概念、技术与挑战[J]. 计算机研究与发展, 2013, 50(1): 146-169.

Meng X F, Ci X. Big Data Management: Concepts，Techniques and Challenges[J]. Journal of Computer Research and Development, 2013, 50(1): 146-169.

[25] Lei L, Shulin Z, Zhilou Y, et al. A big data inspired chaotic solution for fuzzy feedback linearization model in cyber-physical systems[J]. Ad Hoc Networks, 2015, Volume 35: 97-104.

[26] Packard N H, Crutchfield J P, Farmer J D, et al. Geometry from a time series[J]. Physical review letters, 1980, 45(9): 712.

[27] Wu, C. L., K. W. Chau, Y. S. Li. Predicting monthly streamflow using data-driven models coupled with data preprocessing techniques[J]. Water Resources Research, 2009, 45: W08432.

[28] Takens F. Detecting strange attractors in turbulence[M]. Dynamical systems and turbulence, Warwick 1980. Springer Berlin Heidelberg, 1981: 366-381.

[29] 董春娇, 邵春福, 李娟等. 基于混沌分析的道路网交通流短时预测[J]. 系统工程学报, 2011, 26(3):340-345.

Dong C J, Shao C F, Li J,. Short-term traffic flow prediction of road network based on chaos theory[J]. Journal of Systems Engineering, 2011, 26(3):340-345.

[30] Fraser A M, Swinney H L. Independent coordinates for strange attractors from mutual information[J]. Physical review A, 1986, 33(2): 1134.

[31] Rosenstein M T, Collins J J, De Luca C J. Reconstruction expansion as a geometry-based framework for choosing proper delay times[J]. Physica D: Nonlinear Phenomena, 1994, 73(1): 82-98.

[32] Abarbanel H D I, Brown R, Sidorowich J J, et al. The analysis of observed data in physical systems[J]. Rev. Mod. Phys, 1993, 65(4): 1331-1392.

[33] Grassberger P, Procaccia I. Measuring the Strangeness of Strange Attractors[J]. Physica D: Nonlinear Phenomena. 1983, 9(1-2): 189- 208.

[34] Shukuan L, Jianzhong Q, Guoren W, et al. Phase Space Reconstruction of Nonlinear Time Series Based on Kernel Method[C]. In Proceedings of the 6th World Congress on Intelligent Control and Automation, 2006, pp. 4364-4368.

[35] Armstrong J S, Collopy F. Error measures for generalizing about forecasting methods: Empirical comparisons[J]. International journal of forecasting, 1992, 8(1): 69-80.

[36] Theil H. Economic forecasts and policy[M]. Amsterdam: North- Holland Publishing Company, 1958.

Study on prediction of public transportation user group trips based on massive sequence data

FENG Lu, QIAN Yu*, BAI Mengna, YUAN Hua

( School of Management and Economics, University of Electronic Science and Technology of China, Chengdu 611731, China)

In massive sequence data, predicting the behavioral patterns of user groups over a period of time in the future is a very meaningful research endeavor. In this field, research on the behavioral patterns of public transportation user groups is particularly representative and reflective of the main characteristics of urban residents and cities, as public transportation is the primary means by which urban residents travel. To improve the efficiency of public resource use and optimize the management of urban public transportation, it is of great significance to promote the intellectual development of urban computing.

Traffic flow-related prediction research has undergone a long period of development. Previous research considered only the prediction of short-term traffic flow, however the reasonable prediction of long-term traffic flow may provide better services for traffic management. With the emergence of intelligent transportation, people expect to use public transit big data to accurately predict the travel behavior of long-term user groups.

Taking the behavior of public transport user groups as an example, this paper introduces the phase space reconstruction method to predict the nature and regularity of mass transit group sequence behaviors, and uses massive sequence data to model the large-scale system to simulate its dynamic evolution process. However, the phase space reconstruction method faces two problems: one is the selection of number of similar points in the phase space; the other is the quality of the phase space reconstruction.

With respect to the first problem, after the general phase space reconstruction method maps the data to the phase space, the K-proximity method is normally used to find similar points within the time frame for prediction. However, this method is sensitive to the adjacent number of values K and produces a large error. Given these flaws, this paper proposes the similarity inflection point method for the automatic selection of similar points before prediction, that is, the most similar P points are automatically selected for prediction in a large K-near neighborhood. This method not only reduces the complexity of similarity calculation in the prediction process, but also significantly improves the prediction effect.

With respect to the second problem, previous studies have only evaluated the quality of phase space reconstructions through prediction effects. This paper not only measures the quality of the phase space reconstruction from the forecast result, but also compares and defines relationships between different prediction results and phase diagrams through a series of parameter experiments. The parameter experiments show that the phase diagram changes significantly under different parameters, and that there is a certain correlation between the high-quality phase diagram and high-precision prediction. This shows that the phase space reconstruction method can better describe the behavioral patterns of public transportation user groups, and shows the effectiveness of the prediction method used for the phase space reconstruction in this paper.

The final experimental results show that the method in this paper has obvious advantages over other time series prediction methods. The similarity inflection point method proposed in this paper, in particular, has significantly improved the prediction accuracy. At the same time, this paper proposes new ideas for exploring the use of massive (periodic) sequence data for system modeling and predicting group behavior over a period of time.

Massive sequence data; Phase space reconstruction; Similarity; Prediction

2017-12-28

2018-08-27

Supported by the National Natural Science Foundation of China (71572029, 71671027, 71490723, 71271044)

TP311

A

1004-6062(2020)04-0126-009

10.13587/j.cnki.jieem.2020.04.014

2017-12-28

2018-08-27

国家自然科学基金资助项目（71572029、71671027、71490723、71271044）。

钱宇（1978—），女，重庆人；电子科技大学经济与管理学院副教授，博士；研究方向：信息经济学与商务智能。

中文编辑：杜 健；英文编辑：Boping Yan