喷丸强化纯铝表面完整性的数值研究*
2020-09-06
(安徽理工大学机械工程学院,淮南 232001)
机械零部件的失效大多起源于其表面及亚表面,原因在于金属材料表面不能胜任苛刻的服役条件,例如磨损、疲劳、腐蚀和表面氧化等。零部件表面的几何形貌、粗糙度、残余应力状态、加工硬化和显微组织结构等参量共同决定着其失效抗力,这些参量之和统称为表面完整性[1]。因此,提高材料的表面完整性,对于延长机械零部件的使用寿命和发挥材料的潜力起着重要的作用。
喷丸强化是一种十分灵活并且经济高效的表面强化技术,广泛应用于航空航天、车辆、船舶、医药、核电、国防军工和过程机械等领域。在喷丸强化过程中,弹丸流从喷嘴中发射,以20~150m/s的速度冲击工件表面,好似成千上万个小金属锤连续击打受喷表面,使得工件表层材料在再结晶温度下产生拉伸弹塑性变形,不均匀的弹塑性变形会促使材料表面硬化[2],引入残余压应力[3],并诱导表层晶粒细化[4],但也会在受喷表面上产生很多的凹坑,造成一定大小的表面粗糙度[5]。张少平等[6]研究了喷丸强化对TC17钛合金表面完整性,并将喷丸强化提高疲劳寿命的机制归结于引入较深的残余压应力层,较高的表面硬化程度和表层晶粒的细化。钱昂等[7]对AerMet100 钢进行了喷丸强化处理并开展了表面完整性测试,分析了喷丸强化对材料表面形貌、粗糙度、晶粒细化程度、硬度、残余应力和显微组织的影响,发现喷丸强化能够有效提高材料的表面完整性,显著提高了AerMet100钢的疲劳抗力和疲劳寿命。王欣等[8]采用不同强度陶瓷丸喷丸强化FGH96 粉末高温合金,研究了受喷合金的疲劳性能和表面完整性,结果发现适宜的喷丸强化工艺可以缓解结构应力集中对粉末合金疲劳性能的削弱。
喷丸强化效果的影响因素众多,有弹丸种类、弹丸大小、弹丸的喷射速度、弹丸流量、喷嘴的移动速率、喷嘴到待喷表面的距离,喷嘴与待喷表面的夹角、以及待喷材料的力学性能等。工程中通常采用喷丸覆盖率[9]和喷丸强度[10]两个标准化参量来作为喷丸强化的工艺参数,然而不同的喷丸覆盖率和喷丸强度可以得到相同喷丸强化效果。目前喷丸强化工艺参数的优化和确定主要基于试验和操作人员的经验,试验研究喷丸强化过程存在费用高、周期长、实施不便等缺陷,另外需要大量的试错试验才能探究材料的喷丸强化机理[11]。近年来,随着数值计算方法和电子计算机的发展,采用数值模拟的方法研究喷丸强化过程已受到广大研究人员的青睐。现存的喷丸强化数值模型有:单丸冲击模型[12]、对称胞元喷丸有限元模型[13]、随机喷丸模型[14]、耦合DEM-FEM(离散元素法-有限单元法)喷丸有限元模型[15]和基于SPH(光滑粒子动力学)的喷丸有限元模型[16]等。其中,对称胞元喷丸有限元模型和随机喷丸有限元模型较为常用,对称胞元喷丸有限元模型有计算效率高的优点,但不能有效模拟相邻凹坑的搭接和重叠;相反,随机喷丸模型能够模拟相邻凹坑之间的重叠,但计算成本高。
结合对称胞元喷丸有限元模型和随机喷丸有限元模型的优点,本文发展一种新型的喷丸强化有限元模型。在该喷丸有限元模型中,多弹丸连续冲击工件的待喷表面,形成的凹坑中心分布在一个圆周上,基于该圆周上凹坑的分布计算喷丸覆盖率,通过改变弹丸个数分析不同喷丸覆盖率下受喷表面的几何形貌、粗糙度、残余应力、加工硬化和晶粒细化,进而实现数值研究喷丸强化纯铝的表面完整性,以优选喷丸强化工艺参数,进一步促进喷丸强化工艺的工业生产应用。
数值建模
1 本构模型
为了研究喷丸强化纯铝的表面完整性,采用基于位错密度演化的本构模型,表征纯铝材料在喷丸强化过程中的动态力学行为,本构模型的表达式可写为[17-19]:

式中,σ1是材料的初始屈服应力;M是泰勒系数;η是一个材料常数;G是材料的剪切模量;b是BURGERS矢量;rγ˙是分解剪切应变率;0γ˙表示参考分解剪切应变率;m表示与应变率硬化相关的敏感指数;f表示位错胞壁的体积分数;ρw和ρc分别表示位错胞壁和位错胞内的位错密度。在金属材料的塑性变形过程中,位错胞壁和位错胞内的位错密度演化可采用一组耦合方程进行表征[20-21]:
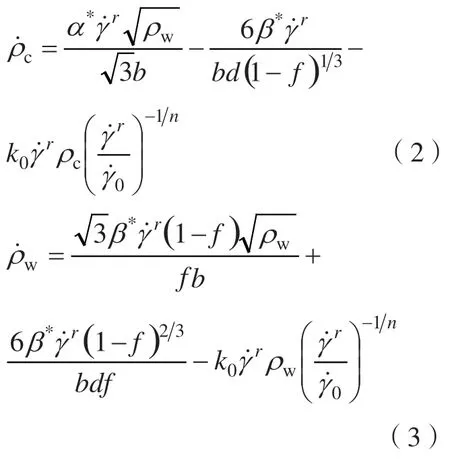
式中,α*、β*和k0分别是与位错的生长、移动和湮没相关的材料参数,n是率相关的敏感指数,d表示平均晶粒尺寸。式(2)和(3)右边的第1项表示位错胞界面上由于FRANK-READ 源激活引起位错胞内的位错生长率;第2项表示位错内的一部分位错转移到位错胞壁并成为位错胞壁的组成部分;第3项表示位错胞内螺型位错的交滑移之间或刃型位错的攀移之间的交互湮没。平均晶粒尺寸与总体位错密度ρt的平方根成反比[20-21]:

式中,K是一个材料常数,总体位错密度可表示为位错胞壁ρw和位错胞内ρc的加权和[20-21]:

式中,f的演化可以采用一个唯像公式进行表征[20-21]:

式中,f0和f∞分别表示f的初值和饱和值,f0>f∞,rγ~是1个用于表征f衰减速率的常数。
式(2)~(6)组成的位错密度演化模型,可用于预测金属材料在塑性变形过程中增加的位错密度和细化的晶粒尺寸[20-21]。对于纯铝材料,基于位错密度演化的本构模型的相关参数如表1[22]所示。
2 有限元建模
基于ABAQUS 有限元分析平台,建立如图1所示的喷丸强化纯铝计算模型,直径为12mm,高2mm。采用三维八节点减缩实体单元(C3D8R)划分网格,通过单元尺寸敏感性分析确定最小网格尺寸为15µm。开发用户材料子程序(VUMAT)将基于位错密度演化的本构模型嵌入有限元软件(ABAQUS/Explicit),赋予单元材料属性,表征纯铝在喷丸强化过程中的动态应力-应变响应。
采用半球壳形的解析刚性体模拟直径3mm的弹丸,刚性体的参考点位于球心,并将整个弹丸的质量赋予在该参考点上。在弹丸的参考点上施加初始速度场,初始速度大小为25m/s,方向垂直于待喷表面。多弹丸冲击待喷表面的位置点分布于距离靶面圆心1.5mm的圆周上,如图1所示,共模拟4、8、16和24个弹丸冲击的工况。对于4个弹丸冲击工况,相邻弹丸在面内的夹角为90°;对于8、16和24个弹丸冲击工况,相邻弹丸之间的面内夹角分别为45°、22.5°和15°。模型的底面固定,上表面承受多弹丸的连续冲击载荷,利用罚函数算法计算弹丸与受喷表面之间的接触,摩擦系数取0.3。

表1 纯铝多尺度本构模型的材料参数Table1 Material parameters of pure aluminum multi-scale constitutive model
结果与讨论
为了定量研究喷丸强化纯铝的表面完整性,在待喷表面上创建一条圆周路径,如图1所示,分析在不同喷丸工况下沿该圆周路径分布的节点位移(表面形貌和表面粗糙度)、残余应力、屈服应力(表面加工硬化)和晶粒尺寸(晶粒细化)。
1 表面形貌和粗糙度
在不同的喷丸工况下,弹丸冲击靶面形成的凹坑形貌如图2所示。显然可见,4个弹丸冲击靶面形成十分鲜明的4个凹坑,并且凹坑的形状和尺寸基本相同,这表明当相邻弹丸在面内的夹角等于90°时,弹丸冲击形成的凹坑互不影响。与4个弹丸冲击工况不同的是,8个弹丸冲击作用下,相邻凹坑之间产生明显的塑性堆积。对于16和24个弹丸的喷丸工况,受喷表面上凹坑的分布仍然呈现出很好的轴对称性,但相邻凹坑之间存在重叠部分,并且重叠部分压盖了它们之间的塑性堆积。
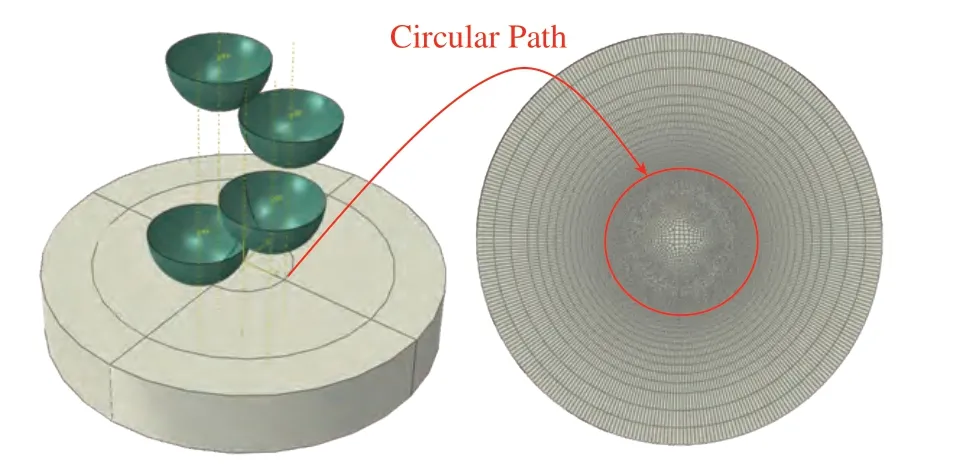
图1 喷丸强化有限元模型Fig.1 Finite element model of shot peening
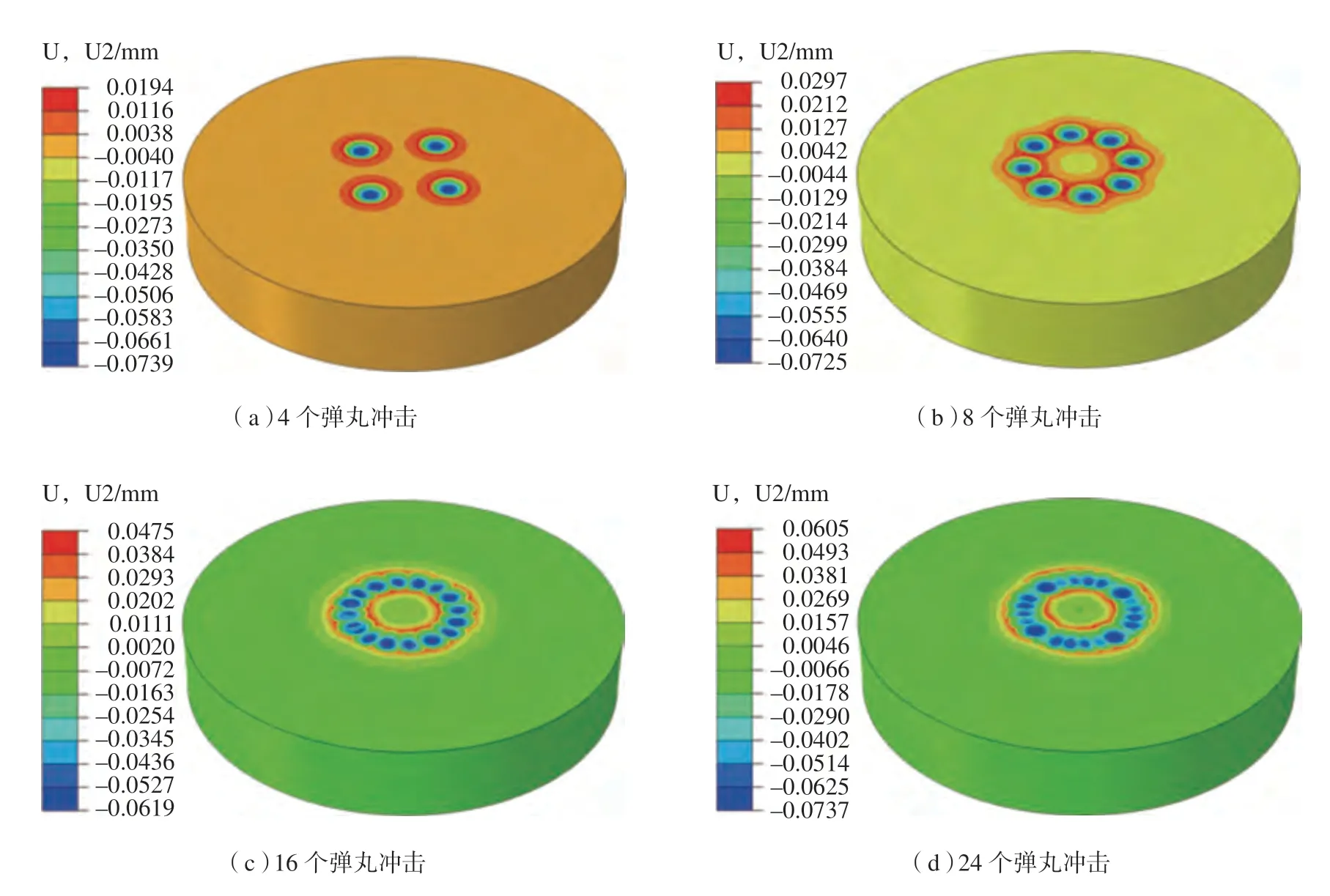
图2 受喷表面形貌Fig.2 Shot-peened surface morphologies
图3 展现了沿圆周路径分布的表面形貌。通过交互比较,更加直观地得到图2的结论。在图3中,随着弹丸个数的增加,沿圆周路径分布的凹坑数目相应增加,以该圆周路径计算的喷丸覆盖率随之增大。对于8个弹丸冲击工况,如图2(b)和3(a)所示,相邻凹坑之间产生塑性堆积,因此可认为8个弹丸冲击可使圆周路径上喷丸覆盖率达到98%,即完全喷丸覆盖率。16和24个弹丸冲击就分别对应圆周路径上200%和300%喷丸覆盖率。基于图3中沿圆周路径(如图1中的红色实线所示)分布的表面形貌,根据算术平均粗糙度的计算公式:
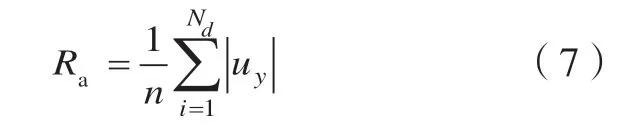
式中,uy表示受喷表面的节点位移和Nd表示节点的个数,可比较不同喷丸工况下的表面粗糙度:对于4个弹丸冲击,Ra=47.1µm;对于8、16和24个弹丸冲击,Ra分别为93.9µm、33.6µm和20.9µm。因此可以得到:随着喷丸覆盖率的增加,受喷表面表面粗糙度随之增大,但达到完全喷丸覆盖率后,受喷表面粗糙度逐渐减小,但减小的幅度也随之减小,表面受喷表面粗糙度逐渐趋于稳定。
2 表面残余应力

图3 沿圆周路径分布的表面形貌Fig.3 Surface morphologies distributed on circular path within shot-peened surface

图4 沿圆周路径分布的表面残余应力Fig.4 Residual stresses distributed on circular path within shot-peened surface
弹丸冲击后,受喷表面不均匀的弹塑性变形会形成表面残余应力,图4给出了沿圆周路径分布的表面残余应力,该残余应力的方向为圆周路径的切向。由图4(a)可见,在多弹丸的连续冲击作用下,受喷表面形成残余压应力和残余拉应力;当弹丸个数由4个增加到8个时,表面残余压应力显著增大,但表面最大残余拉应力变化并不明显;当弹丸个数由8个增大到16个时,表面残余压应力变化不再明显;当弹丸个数进一步增大到24个时,如图4(b)所示,表面残余应力的分布几乎不变。因此可以得到:随着喷丸覆盖率的增加,受喷表面上的残余压应力增大,但达到完全喷丸覆盖率之后,受喷表面残余压应力趋于稳定。然而,从图4中可以看到,在高喷丸覆盖率下受喷表面的局部区域仍然呈现表面残余拉应力状态,这主要归结于相邻弹丸撞击位置的相互作用。多弹丸理想化地依次冲击受喷靶面,圆周路径上有部分节点处于相邻弹丸撞击位置的重叠区域,该区域受到相邻弹丸冲击产生的拉应力作用。
3 表面加工硬化
常规喷丸强化是一种冷加工技术,金属材料表面经过喷丸强化后,其强度和硬度均有所提高[23]。不同喷丸工况下,沿圆周路径分布的表面屈服应力如图5所示,该屈服应力根据式(1)计算得到。由图5(a)可见,当弹丸个数小于8时,受喷表面最大屈服应力基本相同;当弹丸个数增加到16时,受喷表面的最大屈服应力增大至154MPa,比8个弹丸的工况大16MPa。当弹丸个数为24时,由图5(b)可见,相对于8个弹丸的工况,受喷表面的屈服应力进一步增大,但增加的最大幅度只有9MPa。因此可以得到:随着喷丸覆盖率的增加,受喷表面上的屈服应力增大,但达到完全喷丸覆盖率之后,受喷表面屈服应力增加的幅度逐渐减小,表明受喷表面硬化变得愈加困难。
4 表面晶粒细化
近年来的研究发现,喷丸强化诱导材料表面晶粒细化是喷丸技术的微观强化机制[23]。根据Hall-Petch关系式,金属材料的屈服应力与其晶粒尺寸的平方根成反比。因此,从图5中屈服应力的提高可以推断受喷表面的晶粒细化。根据式(4),不同喷丸工况下,沿受喷表面圆周路径分布的晶粒尺寸如图6所示,显然与图5中受喷表面屈服应力分布相对应。由图6(a)可见,当弹丸个数小于8时,喷丸强化诱导材料表面细化的晶粒尺寸基本相同;当弹丸个数增加到16时,受喷表面上最小晶粒尺寸细化至1.3µm,比8个弹丸工况小0.5µm;当弹丸个数为24时,由图6(b)可见,相对于8个弹丸的工况,受喷表面的晶粒尺寸进一步细化,但细化的幅值只有0.2µm。因此可以得到:随着喷丸覆盖率的增加,受喷表面上的晶粒尺寸不断细化,但达到完全喷丸覆盖率之后,受喷表面上晶粒细化的幅度逐渐减小,表明受喷表面的晶粒细化变得愈加困难。
5 表面等效塑性应变
喷丸强化在受喷表面上形成表面粗糙度、残余应力场、加工硬化和晶粒细化都与材料表面的塑性变形有关。塑性变形量可采用等效塑性应变进行表征,图7给出了不同喷丸工况下沿受喷表面圆周路径分布的等效塑性应变,显然与图3~6相对应:当弹丸个数小于8时,受喷表面最大等效塑性应变基本相同;当弹丸个数增加到16时,受喷表面沿圆周路径分布的等效塑性应变随之增大,最大等效塑性应变增大至0.62,相对于8个弹丸工况增加了0.4;当弹丸个数进一步增加至24时,由图7(b)可见,相对于16个弹丸工况,尽管最大等效塑性应变相对于16个弹丸工况仍然增加了0.4,但大部分受喷表面等效塑性应变的变化并不明显,即受喷表面等效塑性应变与表面粗糙度、残余压应力、屈服应力以及晶粒细化的变化趋势保持一致。

图5 沿圆周路径分布的屈服应力Fig.5 Yield stresses distributed on circular path within shot-peened surface
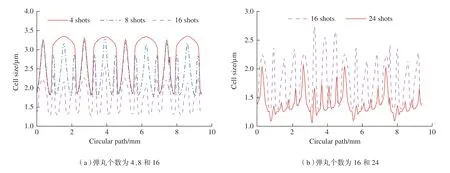
图6 沿圆周路径分布的晶粒尺寸Fig.6 Cell sizes distributed on circular path within shot-peened surface

图7 沿圆周路径分布的等效塑性应变Fig.7 Equivalent plastic strains distributed on circular path within shot-peened surface
结论
(1)随着喷丸覆盖率的增加,表面粗糙度和表面残余压应力增大,但达到完全喷丸覆盖率后增加的幅度逐渐减小并逐渐趋于稳定。
(2)受喷表面的加工硬化和晶粒细化随着喷丸覆盖率的增大变得愈加困难。
(3)受喷表面的塑性变形与表面粗糙度、残余压应力、屈服应力以及晶粒细化的变化趋势保持一致。
