凹坑结构对麻面管流动与传热特性的影响分析

2020-02-24闫顺林

科学技术与工程 2020年1期

闫顺林, 张莎, 何仑

(华北电力大学能源动力与机械工程学院,保定 071003)

纵向涡强化传热技术一直是强化换热研究的重点,除在换热表面安装纵向涡发生器外,常将换热管表面加工成非光滑表面异型管以增强换热[1-4]。而非光滑表面结构参数决定了换热管性能优良与否,为此,中外学者对各种异型管粗糙表面结构进行了大量研究。

刘晓兵[5]对酒窝板强化换热进行数值模拟,得出窝径为12 mm、窝高4 mm、窝距为21 mm时换热板片的换热及流动阻力达到最佳匹配。Li等[6]对交错双斜向内肋换热管进行了数值研究,结果表明斜向内肋在低Re区使换热强化,努塞尔数Nu和阻力系数f均随肋高增大而增大,斜度为45°的内肋换热效果较优。贾宝光[7]对不同内肋结构参数的间断横纹内肋管进行模拟研究,得出在Re=400时,结构参数c=50°、p=5 mm、e=0.6 mm、a=2.7 mm的内肋管换热效果最好,综合换热评价指标可达2.5。闫顺林等[8]对麻面管管内凸胞侧进行模拟研究,得出不同Re范围的较优结构参数也不同,麻面管比光管的Nu提高16%～40%,f增加15%～53%,综合传热性能指标为1.05～2.5；Burgess等[9]对流体通道内酒窝坑的影响进行实验研究,得出在Re=12 000～70 000下,通道局部和平均努塞尔数均随酒窝深度的增加而增加。

现提出一种新型麻面换热管,使用麻面凹坑结构诱导流体域产生涡流来达到增强换热的目的。基于大部分已知文献为对流体流经异型管凸胞侧的研究,主要对流经管外不同高径比凹坑的情况进行分析,研究凹坑结构对麻面管传热与流动特性的影响。

1 数值模拟方法

1.1 物理模型及网格划分

麻面管物理模型如图1所示。为研究不同凹坑高径比h/d在不同进口油速v下对φ22 mm×2.4 mm麻面管传热与流动特性的影响,在凹坑深度h=0.9 mm的前提下,令凹坑直径为1.5、1.6、1.7、1.8、1.9、2.0 mm分别获得高径比为0.6、0.563、0.529、0.5、0.474、0.45的凹坑结构,各模型具体参数如表1所示。

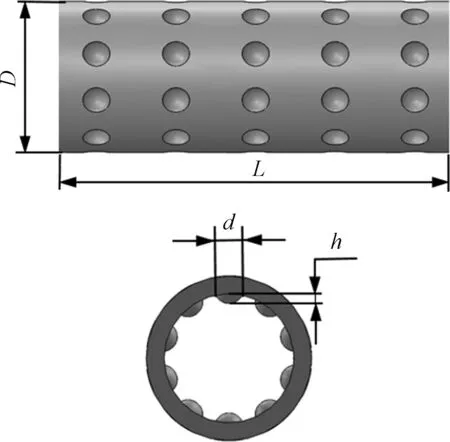
麻管管长为L,外径为D,凹坑直径为d,凹坑深度为h图1 麻面管物理模型Fig.1 Physical model of pitted pipe

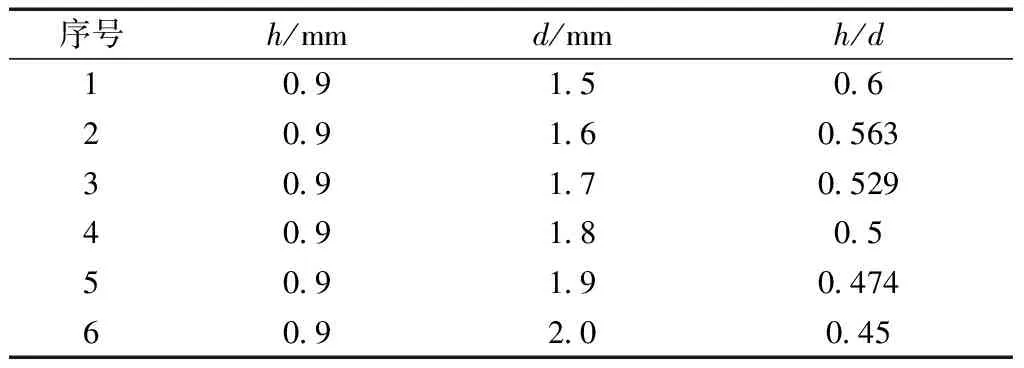
序号h/mmd/mmh/d10.91.50.620.91.60.56330.91.70.52940.91.80.550.91.90.47460.92.00.45

利用Workbench对计算模型进行网格划分,并在流体域与管壁两侧的接触面利用膨胀层进行局部加密,以提高近壁处数值求解的准确度,网格划分如图2所示。对不同网格数量麻面管的模拟计算结果如图3所示,可看出网格数86万的Nu与f均处于稳定状态,说明网格密度已满足模拟精度要求。为节省计算时间,选择网格数为86万进行模拟计算。

图2 计算模型网格划分Fig.2 Grid division of the computing model

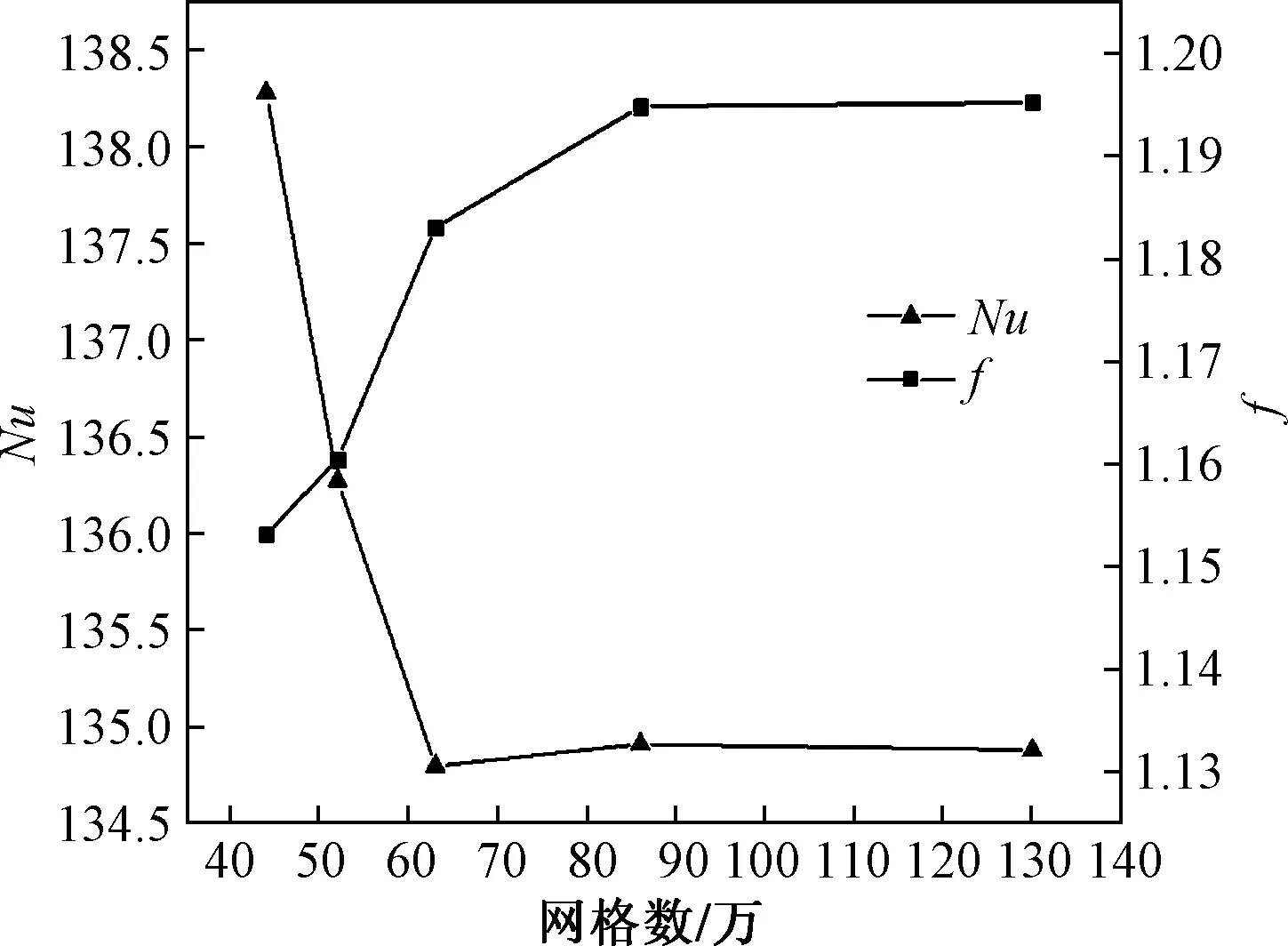
图3 网格无关性验证Fig.3 Verification of grid independence

1.2 数学模型及数据处理方法

润滑油横掠麻面管三维稳态流动与传热满足质量、动量和能量守恒定律,基本方程[10]如下：

质量守恒方程:

(1)

动量守恒方程:

(2)

流体域能量守恒方程:

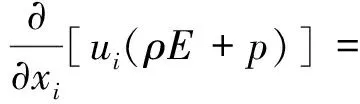
(3)

固体域能量守恒方程:

(4)

式中:i，j=x，y，z；u为流体速度,m/s；p为压力,Pa；ρ为密度,kg/m3；keff为有效热导率,W/(m·K)；E为内能,J/kg；T为温度,K；Sh为热源项,J；Jj′为组分扩散通量；τij为应力张量；λ为固体导热系数,W/(m·K)。

为比较不同高径比凹坑结构对麻面管传热与流动特性的影响,使用努塞尔数Nu与阻力系数f进行数据处理,其定义式为[11]

(5)

(6)

式中:h′为换热管平均对流换热系数,W/(m2·K)；de为换热管当量直径,m；λ为润滑油导热系数,W/(m·K)；Δp为润滑油进出口压力差,Pa；ρ为润滑油密度,kg/m3；v为润滑油平均进口流速,m/s。

1.3 边界条件及数值计算方法

换热管材质为紫铜,管内走水,管外走油,水与紫铜的物性参数如表2所示。DTE24润滑油物性参数引自文献[12]。润滑油黏度设置成随温度线性变化,密度、导热系数等其他物性参数设置为常数[12]。进油口与进水口设置为速度入口条件,进口油温50 ℃,进口水温30 ℃,进口平均水速3 m/s；出油口和出水口均设置为压力出口条件；管壁固体域与两侧流体域接触面均设置为耦合壁面边界条件,耦合交界面的温度及热流密度连续；外壁面设为无滑移绝热壁面。

表2 水与紫铜的物性参数Table 2 Physical properties of water and copper

湍流模型选择RNGk-ε,提高精度且适应低雷诺数黏性流动与近壁湍流旋涡[15]；压力与速度梯度耦合选用Simplec算法求解；壁面采用增强壁面函数法处理；动量、能量方程及湍动能耗散率采用二阶迎风离散格式；模拟结果各项残差收敛值达到10-6精度。

2 计算结果及分析

2.1 凹坑场态分析

为分析不同高径比凹坑结构对麻面管流动特性的影响,在麻面管截面z=62.8 mm处的速度矢量图与流线图,选取某部位凹坑的局部放大图进行详细分析,取样点如图4所示。

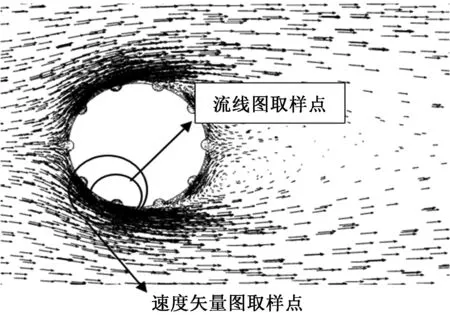
图4 麻面管流动特性分析凹坑取样点Fig.4 Pit sampling areas of pitted tubes flow forcharacteristics analysis

v=1.8 m/s时,z=62.8 mm截面处的流线图如图5所示,随高径比越小,凹坑内的旋涡区越扁平；高径比(h/d=0.563)偏大时,涡结构偏向凹坑后缘；高径比(h/d=0.45)偏小时,涡结构偏向凹坑底部。这是由于流体冲击凹坑后缘进入凹坑,动能惯性使大部分流体沿凹坑周缘旋转流动,随高径比越小,凹坑越扁平,回流形成的涡形越扁平。高径比偏大时,流体从主流区进入凹坑的偏转角度相对较小,冲击凹坑后缘获得的动能较小,且凹坑周缘反向摩擦力使动能进一步减小且产生较大流速梯度,同时产生的压力梯度使前缘高压区压迫旋涡偏离凹坑中心至后缘；高径比偏小时,流体偏转获得的动量较大,使反向摩擦力的影响较小,旋转流主要受凹坑形状影响,凹坑越扁平,涡形越偏向凹坑底部。

图5 v=1.8 m/s时z=62.8 mm截面处的流线图Fig.5 Streamline diagram at z=62.8 mm section when v=1.8 m/s

v=1.8 m/s时,z=62.8 mm截面处的速度矢量图如图6所示，可知凹坑高径比h/d=0.5的旋涡区充盈度最好；高径比h/d=0.563的凹坑周缘低速旋转流动状态良好,但与高径比h/d=0.5相比明显旋转流的流速较低,在旋涡中心容易发生滞流；高径比h/d=0.45的流体大多沿凹坑周缘快速旋转流出,凹坑中心旋转流较少。这是由于高径比(h/d=0.45)偏小,凹坑后缘过于平缓,只有少量主流区流体被拦截进入凹坑,且进入凹坑流体的偏转角度较大,使具有较大动能惯性的旋转流体紧贴凹坑周缘流出。当高径比(h/d=0.563)偏大,流体偏转进入凹坑的动能较小,凹坑周缘反向摩擦力使流体动能进一步减弱,致使凹坑旋涡中心因流速过低容易出现滞流现象。

图6 v=1.8 m/s时z=62.8 mm截面处的速度矢量图Fig.6 Velocity vector diagram at z=62.8 mm section with v=1.8 m/s

v=1.8 m/s时,z=62.8 mm截面处的温度矢量图如图7所示，可知凹坑h/d=0.5的麻面管比h/d=0.45与h/d=0.563的流体域温度变化更明显,说明麻面管的传热性能随凹坑高径比增加不是单调变化关系,且h/d=0.5时的传热效果较好。这是由于高径比偏小(h/d=0.45)时,进入凹坑的旋转流较少且流速较快,不利于管壁边界层能量与动量的充分与及时交换；当高径比偏大(h/d=0.563)时,结合速度场可知凹坑低速旋涡区充盈度较高有利于传热,但凹坑面积的减小使麻面管总有效传热面积大幅度减小,抑制了增强传热的优势,使麻面管传热性能减弱。

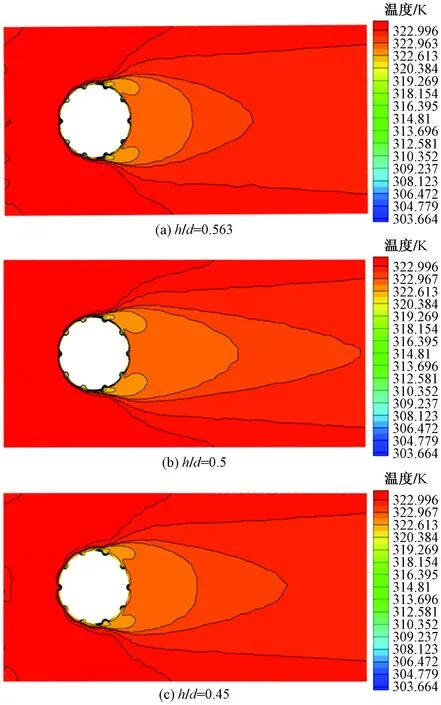
图7 v=1.8 m/s时z=62.8 mm截面处的温度矢量图Fig.7 Cloud diagram of temperature at z=62.8 mm section with v=1.8 m/s

2.2 凹坑结构对流动与传热特性的影响

不同凹坑直径d下Nu与f随油速v变化曲线如图8所示，可知随着进口油速的增加,不同凹坑结构麻面管与光管的Nu均升高,f均减小。且麻面管的Nu均高于光管,f均小于光管。造成麻面管Nu较高的原因一方面是由于凹坑的存在增加了换热管的总有效传热面积,另一方面凹坑的存在加强了管壁周围的涡流扰动,使能量与动量的交换加剧。造成麻面管f较小的原因是凹坑内部存在着低速旋流,与凹坑外部流体接触使流经凹坑后的主流速度降低,湍动能损耗减小；凹坑内部的反转气流在凹坑底部产生的摩擦阻力与来流相反,摩擦阻力在凹坑底部作为一种附加动力产生推动效应[16]。两种效应的叠加使凹坑具有减阻作用,使相同进口油速横掠下的麻面管阻力比光管更小。同时由图8可知d=1.8 mm时为Nu与f的转折点,更加明确的数据关系显示如图9所示。

不同进口油速v下Nu与f随h/d变化曲线如图9所示，由图9(a)可知在相同进口油速下,h/d从0.45～0.5的Nu呈上升趋势,但h/d=0.5～0.6的Nu呈下降趋势,h/d=0.5处为Nu最高点。造成这种现象的原因是在h/d=0.45～0.5内,凹坑随高径比越小越平缓,越不利于附近流体碰撞凹坑后缘,使凹坑内旋转流较少不利于传热,同时流体冲击凹坑后缘进入凹坑的偏转角较大使旋转流流速较高,在凹坑停留时间较短也不利于传热。在h/d=0.5～0.6内,陡直的后缘利于流体进入凹坑产生低速旋转流,但高径比越大,凹坑直径越小,麻面管的有效传热面积越小,使麻面管传热效果再次降低。且由h/d=0.5两侧的降低差值可知,有效传热面积的减小对麻面管的传热性能影响较大。

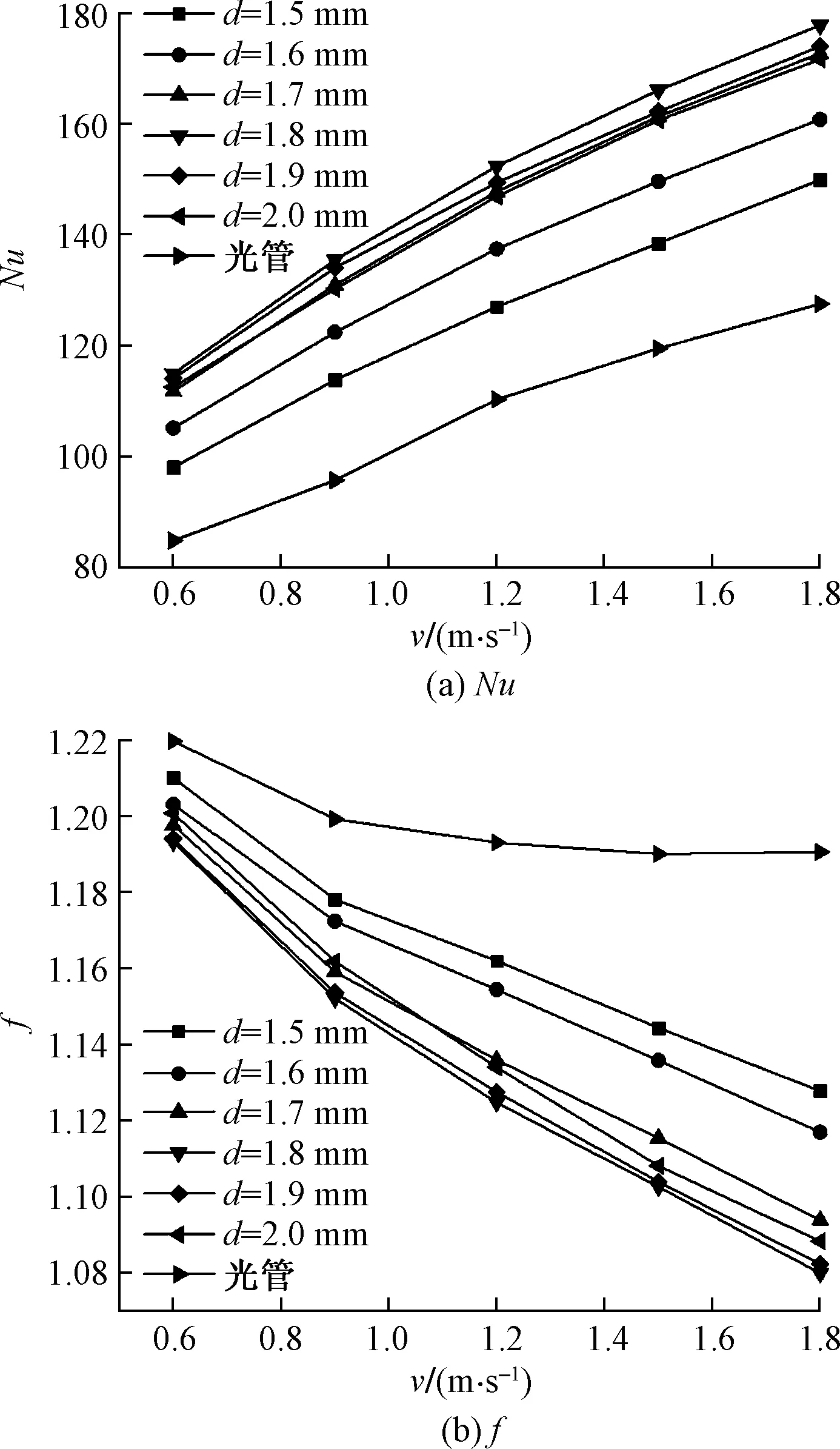
图8 不同凹坑直径d下Nu与f随油速v变化曲线Fig.8 Curves of Nu and f with different pit diameters d and different oil speeds v

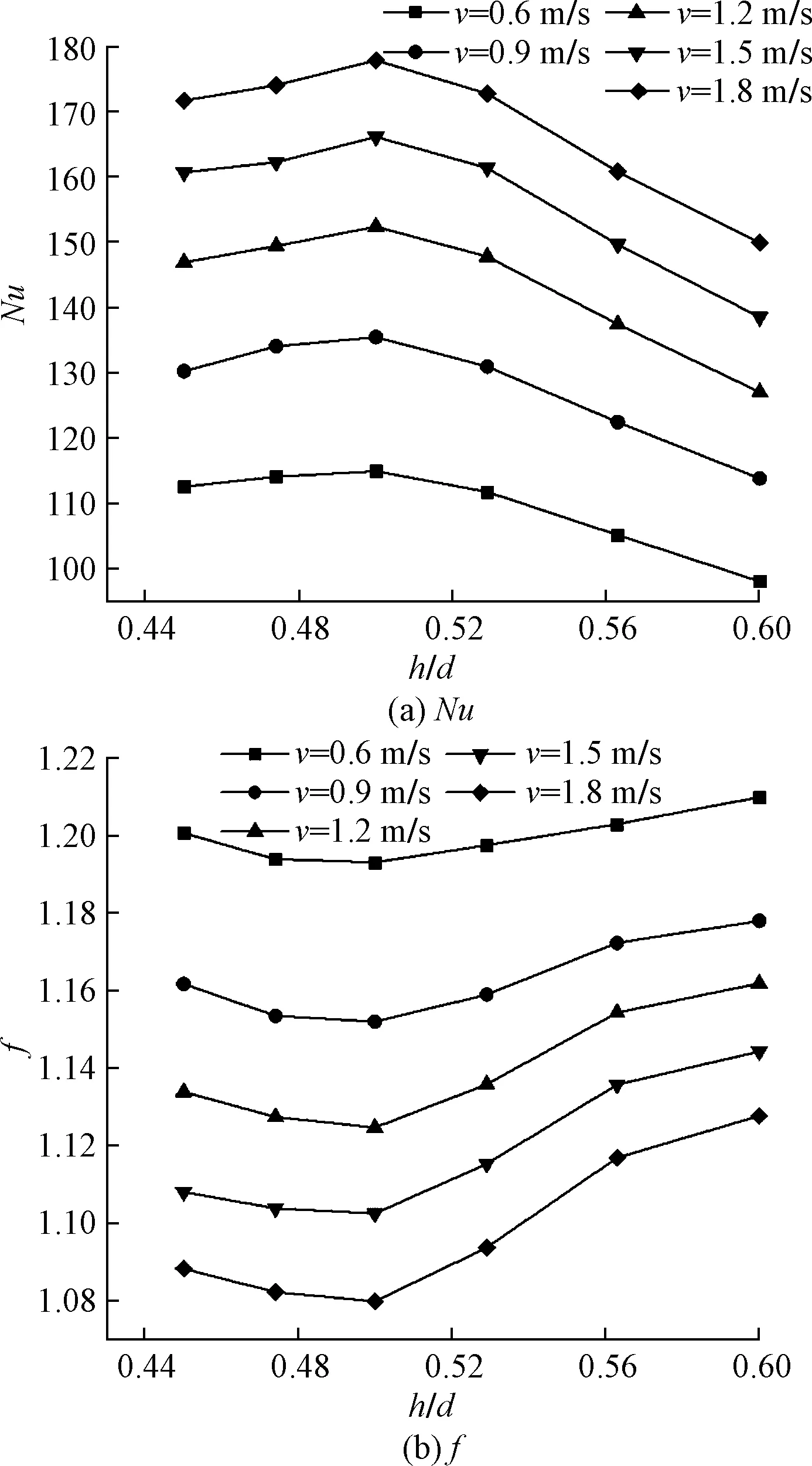
图9 不同进口油速v下Nu与f随h/d变化曲线Fig.9 Curves of Nu and f with different in let oil speeds v and different h/d

由图9(b)可知在相同进口油速下,h/d=0.45～0.5的f呈下降趋势,但h/d=0.5～0.6的f呈上升趋势,在h/d=0.5处达到f最低点。这是由于在h/d=0.45～0.5内,高径比越小,主流区进入凹坑的流体偏转角度越大,获得的动量惯性越大,高速流体经凹坑周缘后汇入主流时对主流区的冲击越大,使麻面管阻力越大；在h/d=0.5～0.6内,高径比越大,麻面管的凹坑越深,越容易在凹坑内部形成流动死区使麻面管阻力增大。结合Nu与f可知,凹坑高径比h/d=0.5时,麻面管的Nu最高,f最低,该凹坑高径比下麻面管的综合传热性能最好,此时为本研究范围内的最优凹坑结构。