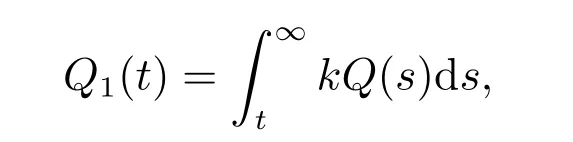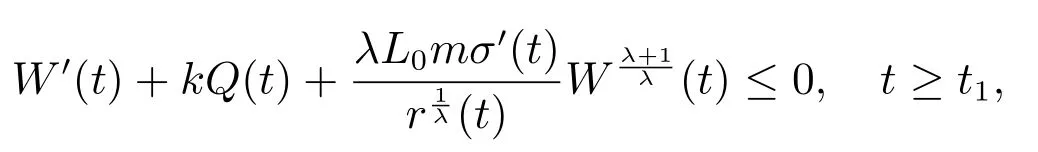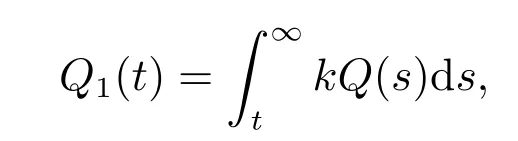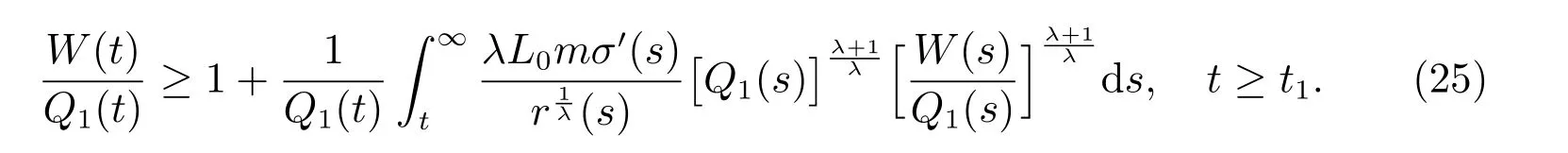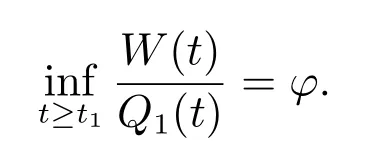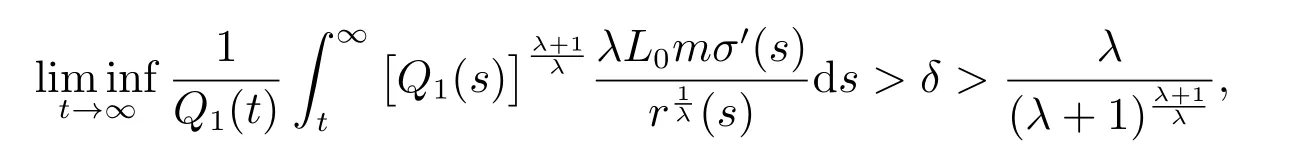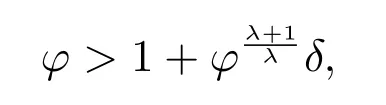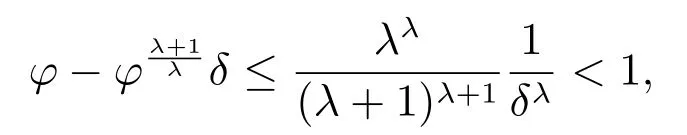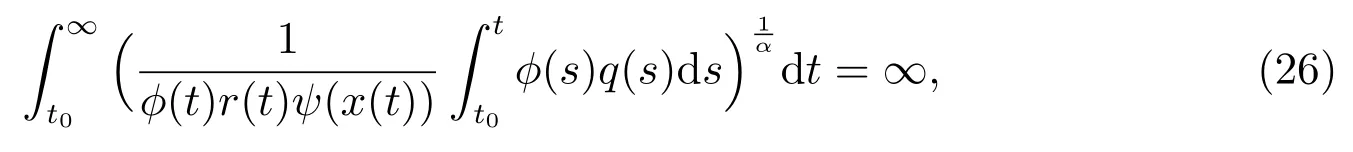二阶拟线性中立型时滞微分方程的振动性

2020-09-05李文娟李书海

工程数学学报 2020年4期

关键词：增函数赤峰二阶

李文娟, 李书海, 汤获

(1- 赤峰学院数学与统计学院，赤峰 024000; 2- 赤峰学院应用数学研究所，赤峰 024000)

1 引言

本文考虑二阶拟线性中立型微分方程

其中z(t)=x(t)+p(t)x(τ(t)), r ∈C1([t0,∞),R), p 和q ∈C([t0,∞),R), α 和β 是两个常数.本文总假设下列条件成立：

(H1): α>0, β >0;

(H2): 0 ≤p(t)≤1, q(t)≥0;

(H3):

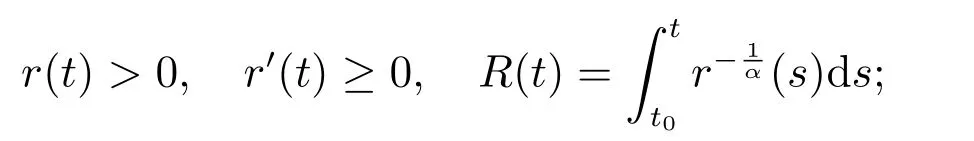
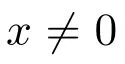
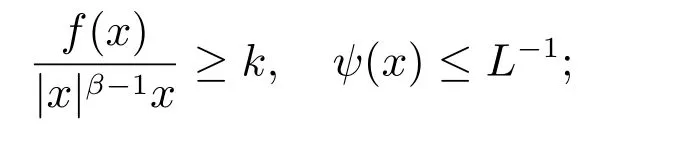
(H5):

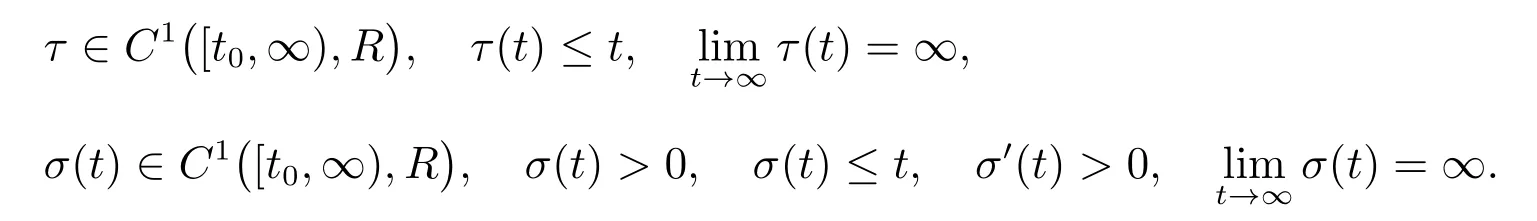
设Tx=min{τ(T),σ(T)}, T ≥t0.若x ∈C1([Tx,∞),R)适合

r(t)ψ(x(t))|z′(t)|α−1z′(t)∈C1([Tx,∞),R),

且在[Tx,∞)上满足方程(1)，则称x 为方程(1)的一个解.本文仅考虑方程(1)的非平凡解，即对一切t ≥Tx，方程(1)在[Tx,∞)上的解x 满足sup{|x(t)| : t ≥T} > 0 情形.如果方程(1)的解有任意大的零点，则称其解为振动的，否则，称它为非振动的.若方程(1)的一切解均为振动的，则称方程(1)为振动的.

近年来，二阶拟线性中立型微分方程在自然科学和工程技术中的应用日益广泛，许多学者对其振动性的研究有着浓厚的兴趣.2010 年，文献[1]考虑了拟线性中立型微分方程

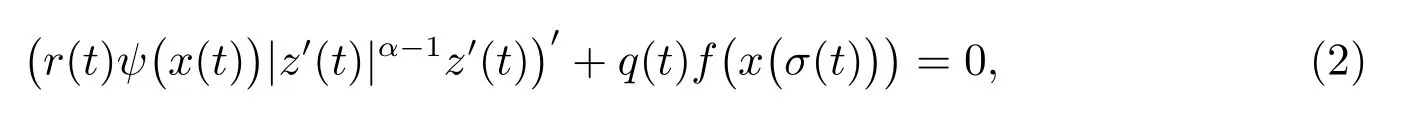
其中

2011 年，文献[2]考虑了Emden-Fowler 中立型方程

其中

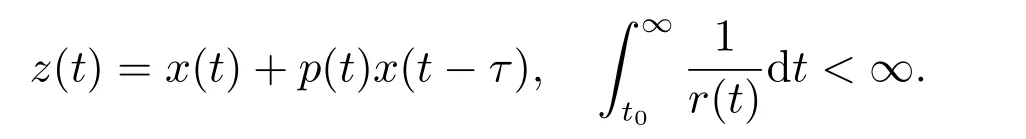
2012 年，文献[3]考虑了拟线性中立型方程

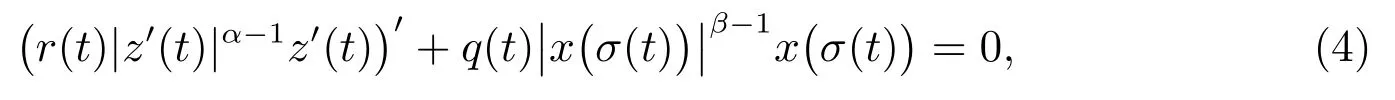
其中

z(t)=x(t)+p(t)x(τ(t)), α ≥β >0.

2015 年，文献[4]进一步研究了方程(4)，分别给出了当α ≥β >0 和β ≥α>0 时，方程(4)新的振动准则，改进了文献[3]的结果.

最近，Agarwal 等人在文献[5]中考虑了半线性中立型微分方程

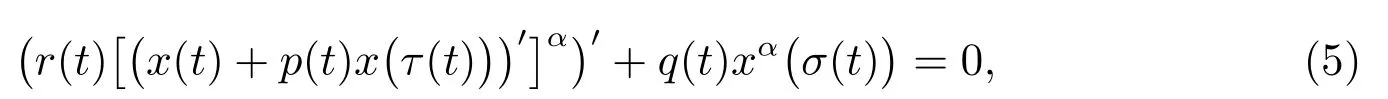
讨论了非正则条件，即

下方程(5)新的振动准则，改进了文献[1]的结果.我们注意到，虽然Emden-Fowler 中立型方程(3)不含在半线性方程(5)中，但它在粒子物理学中有非常重要应用，且上述方程(2)–(5)均为本文所考虑方程(1)的某些特例.在上述工作的基础上，本文通过导出新的Riccati 不等式，利用积分平均方法给出方程(1)新的振动准则，所得结果改进了文献中已有结果.

下面，我们分别讨论在非正则条件(6)和正则条件

下方程(1)的解的振动性.

2 主要结果及证明

定理1设条件(H1)–(H5)和(7)成立，且存在函数ρ ∈C1([t0,∞),R+)和0 < m ≤1，使得

成立，其中

则方程(1)振动.

证明设x 为方程(1)的一个非振动解.不失一般性，不妨设x 为最终正解，则存在t1≥t0，使得当t ≥t1时，有x(t) > 0, x(τ(t)) > 0, x(σ(t)) > 0.如果x 为最终负解，可用同样的方法来讨论.由方程(1)和假设条件可得到

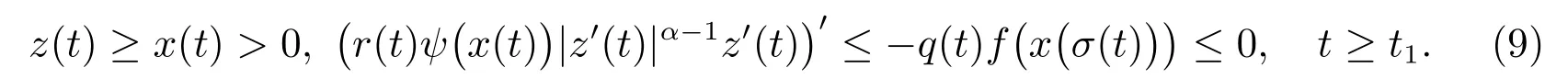
因此，r(t)ψ(x(t))|z′(t)|α−1z′(t)是非增函数且z′(t)最终保号，于是z′(t)仅有两种可能.可断言z′(t)>0，否则假设z′(t)<0, t ≥t2≥t1.

利用函数r(t)ψ(x(t))|z′(t)|α−1z′(t)是非增函数可知，存在正常数h，使得

即

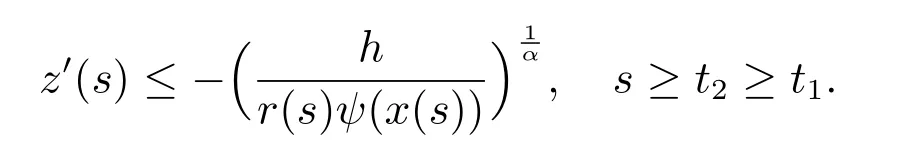
对上式从t2到t 积分，得

另一方面，由于r(t)ψ(x(t))|z′(t)|α−1z′(t)是非增函数且z′(t)>0，故有

r(t)ψ(x(t))(z′(t))α≤r(σ(t))ψ(x(σ(t)))(z′(σ(t)))α, t ≥t1,

即

又由τ(t)≤t 和z′(t)>0，可得

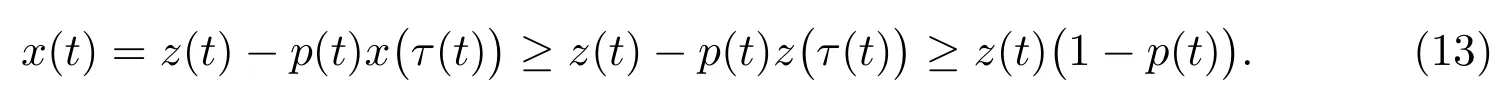
再由条件(H4)、方程(1)和(13)式，得

其中Q(t)=q(t)[1 −p(σ(t))]β.定义函数

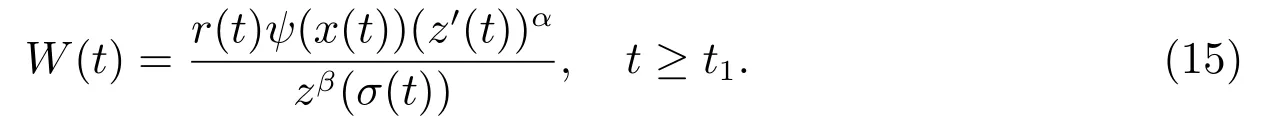
显然W(t)>0.利用(13)–(15)式，可得

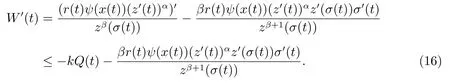
接下来，我们分两种情况讨论(16)式：

1) 当α ≤β 时，由(12)式和(16)式可得

令

又

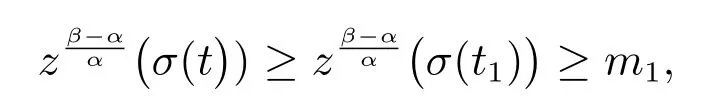
故有

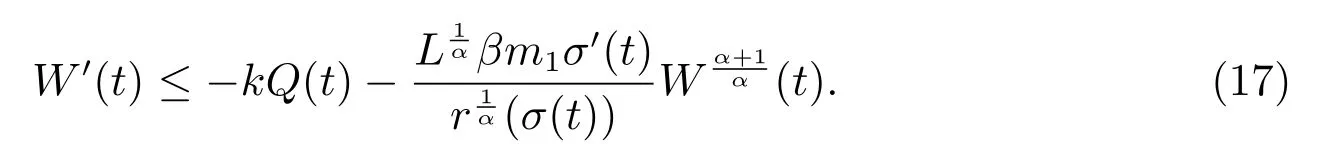
2) 当α>β 时，由(14)式得

(r(t)ψ(x(t))(z′(t))α)′≤−kQ(t)zβ(σ(t))≤0,

即

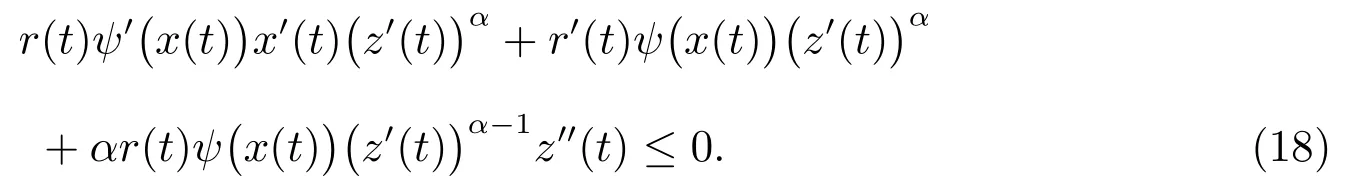
由(18)式可得z′′(t)≤0，从而有

再由z′(t)≤z′(σ(t))和(16)式可得

即

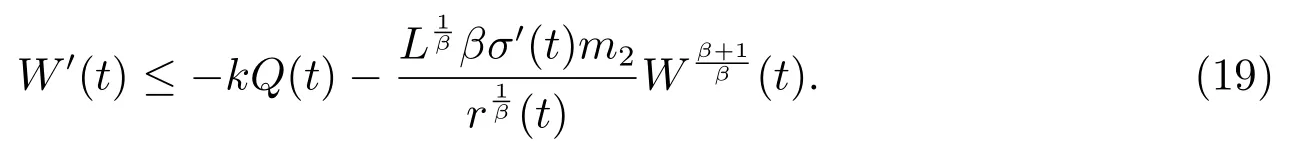
由条件(H3)知r′(t)≥0，又由(16)式知W′(t)≤0.综上，由(17)式和(19)式，我们有

其中

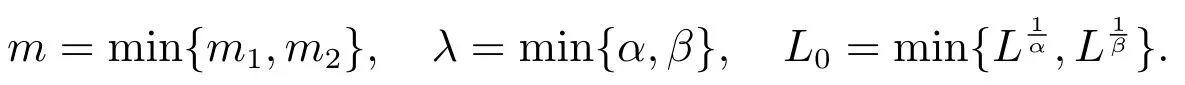
将(20)式两端同时乘以ρ ∈C1([t0,∞),R+)，并从t1到t 积分，可得

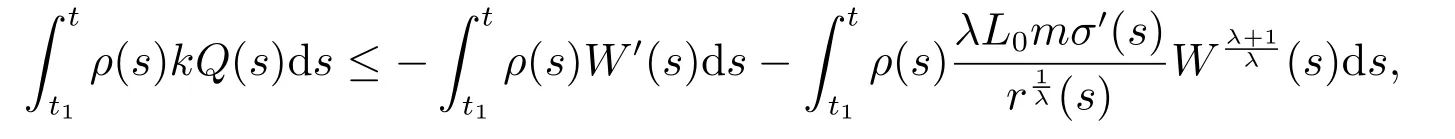
即

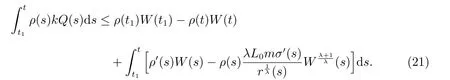
借助不等式

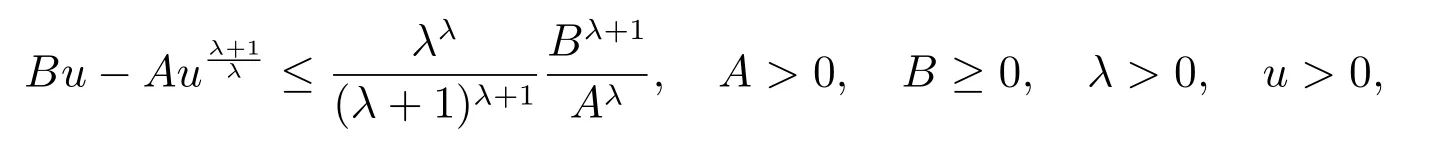
和(21)式，可得

由(22)式可得

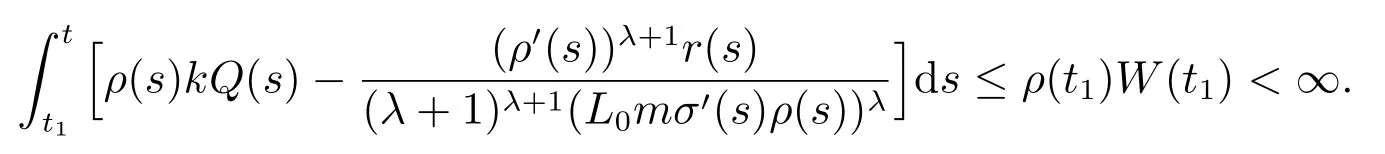
当t →∞，易知上式与条件(8)矛盾，故x 是方程(1)的振动解.

注1定理1 是将二阶线性微分方程

(r(t)x′(t))′+q(t)x(t)=0

的Leighton-Wintner 振动定理推广到拟线性中立型微分方程(1)情形，从而使前者成为定理1 的特例.另外，在本文中，若令方程(1)中的ψ(x(t)) = 1, f(x) = |x|β−1x，则方程(1)退化为文献[3]中的方程(1).但不同的是，文献[3]中的定理2.1 仅考虑方程(1)在α ≥β > 0 条件下的振动结果，而本文的定理1 则考虑方程(1)在α > 0, β >0 条件下的振动结果.

定理2设条件(H1)–(H5)和(7)成立，存在0