非线性尘埃等离子体孤立子波变分迭代解

徐建中, 汪维刚, 莫嘉琪

(1- 亳州学院电子与信息工程系，亳州 236800; 2- 合肥幼儿师范高等专科学校基础部，合肥 230011;3- 安徽师范大学数学与统计学院，芜湖 241003)

1 引言

近来在全球气候变暖的情形下，加上人为等因素引起的大气反常的事件，导致了大气气候的极端事件出现的几率增加，譬如沙尘暴和雾霾等情形不断地出现.大气中尘埃的扩散现象对人们的生产和生活带来了巨大的灾害.这种气候对空气污染受到学术界的很大的关注.为改善大气的质量和控制空气中尘埃的污染，人们需要清楚大气中尘埃颗粒物的分布状况.但是空气中尘埃颗粒物的产生有许多因素，这样就影响了控制环境污染措施的制定.因此，我们需要对大气尘埃颗粒物的了解并要在对气象和尘埃污染数据监测和预报的基础上开展更精细的计算，然后由计算的结果采取合适的措施.这样有助于减少相应的环境污染和灾害，促使大气环境改善.

近年来，许多学者对大气尘埃的研究十分重视[1,2]，Zhao 等对等离子体分离流的燃烧和控制作了研究[3]，Zhang 等对非恒温的等离子体作的分析[4]，Wang 等研讨了一类等离子体在屏障排放状态下的影响[5]，冯依虎等求出了大气量子等离子体孤立子波的渐近解[6]，很多科学工作者还研究了尘埃振动调制方面的稳定性[7]，Duan 等研究了一类尘埃等离子体的非线性波[8,9]，何广军等讨论了尘埃颗粒大小及尘埃荷电量等离子体波的作用[10]等问题.

大气尘埃等离子分布的规律先是通过一维KdV 方程描述的，许多学者作了很多的研究.是将横向非线性波通过KP(Kadomtsev-Pctviashvili)方程来描述的.为了对大气尘埃等离子体扩散有更深入的了解，一些科学工作者还对二维Einstein 凝聚系统做了讨论[11,12].

关于非线性方程的问题，目前已经有较多改进的近似求解方法.作者等也用许多渐近的方法讨论了一类非线性孤波、等离子体、尘埃和有关大气物理问题[13-29].本文是用一个泛函分析的广义变分迭代方法求得了一类广义尘埃等离子体非线性孤立子波方程的渐近解析解.

二维低频尘埃等离子体的无量纲流体动力学系统可表示为

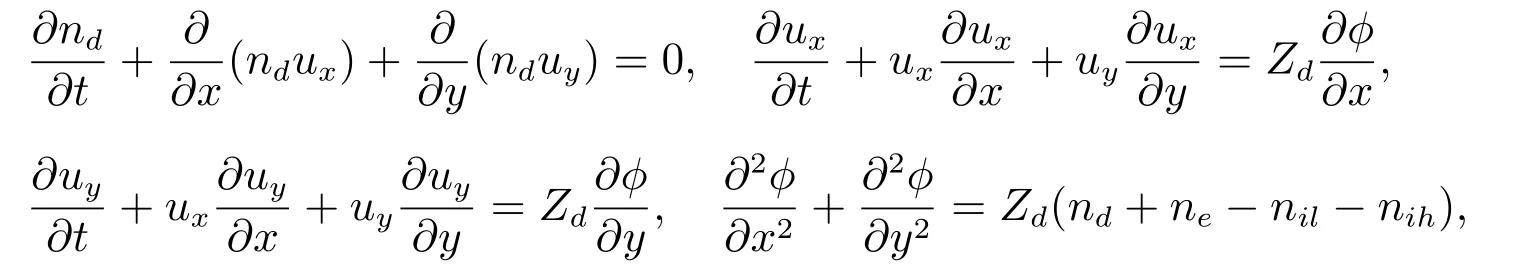
上式

nd=Ail0exp(−sϕ), nih=Aih0exp(−β1sϕ),

ne=Ae0exp(−β1sϕ), nil=Ail0exp(−sϕ),

而ux, uy为尘埃体在x 与y 的速度分量，md, nd为尘埃颗粒的质量和密度，Qd= eZd是尘埃颗粒上的荷电量，

而TeTil和Tih是电子、低温离子和高温离子的温度.

2 典型尘埃等离子体方程孤立子波解

设电子和离子的流速小于热运动速度，作一些变量变换，可得广义KP 方程

作如下行波变换

这里ki(i=1,2,3)为常数.由式(2)得方程(1)以自变量s 的常微分方程

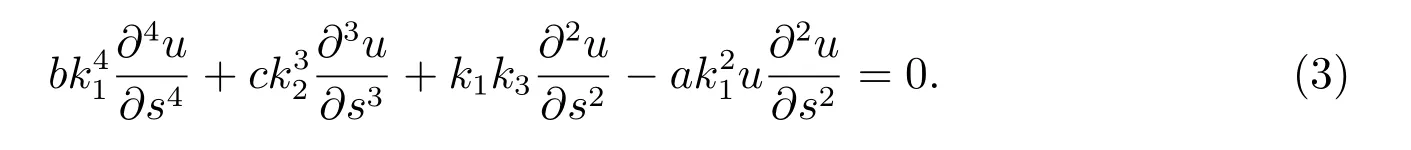
由于方程(3)是具有代数型项的非线性常微分方程，因此，现采用双曲函数待定系数的方法来求孤立子波解[1].设微分方程(3)具有如下的形式的待定解

这里A1, A2, B0为待定常数，而w 满足微分方程

易知，方程(5)有解

由(4)和(5)式有

将式(4),(7)–(10)代入常微分方程(3)，可得

合并上式中的同类次幂的项，且设各次幂项的系数为零，得到

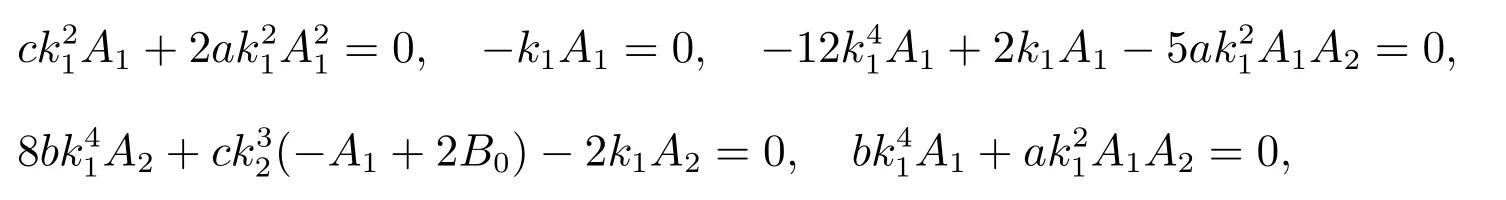
由上面诸式得到

这里k1, k2满足

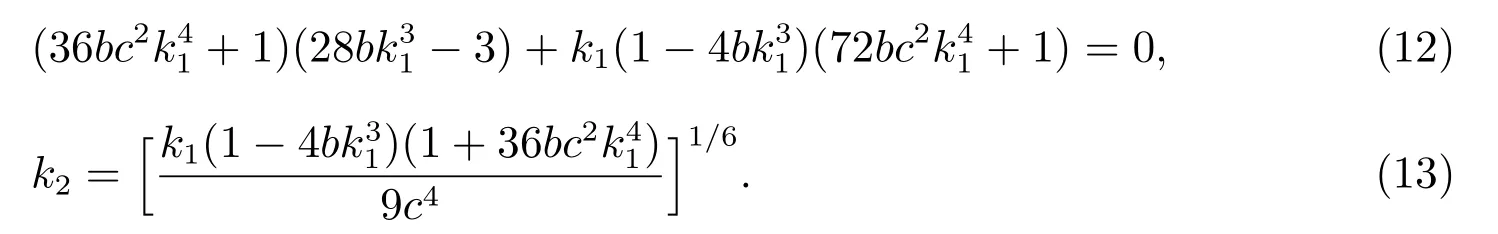
将式(11)和式(6)代入式(4)，可得广义KP 方程(1)如下孤立子波解

今取无量刚参数a = b = c = k2= 1, k1= 1/4，则式(14)表示的孤立子波的曲线图形，如图1 所示.

再选取无量刚参数a = b = c = k1= k2= 1，则式(14)的孤立子波曲线的图形，如图2 所示.

图1: 式(14)的孤立子波曲线 (a=b=c=k2 =1, k1 =1/4)

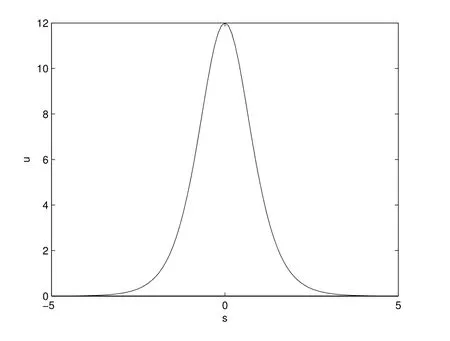
图2: 式(14)的孤立子波曲线(a=b=c=k1 =k2 =1)

由行波变换(2)，便得到广义KP 方程(1)的孤立子行波解

其中k1, k2由式(12),(13)决定.

3 广义尘埃等离子体方程孤立子波解

现讨论二维尘埃等离子体低频振动广义非线性扰动KP 方程

这里a, b, c 是常数；f(u)是低频尘埃声波扰动项，此扰动项为粒子之间的碰撞、电子附着等原因引起的，不妨设它为充分光滑的有界函数.

在变换(2)下，广义非线性扰动KP 方程(16)转化为常微分方程

现用广义变分迭代的方法[30]求尘埃等离子体低频振动广义扰动KP 方程(17)式近似孤立子波解析解.

构造一个泛函

计算泛函(18)的变分

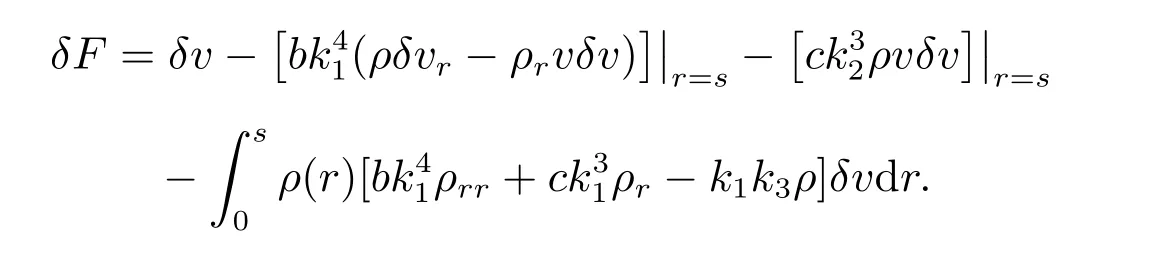
根据变分的极值理论，取δF =0，得到

上述初值问题(19)–(21)的解ρ(r)为

这里

因此，由式(18),(22)，构造如下迭代式

这里ki(i=1,2,3), di=1,2 由式(12),(13)和(23)决定，而u0是初始近似函数.由变分迭代式(24)，当选取初始近似以后，就可得依次得到un(s)(n=1,2,···).

再由变换式(2)，可得广义扰动KP 方程(16)的第n 近似孤立子波行波解un(k1x+k2y −t)(n=0,1,2,···)：

因此，我们得到了函数序列un(t,x,y)(n=0,1,2,···)，由变分理论有如下引理[30].

引理1un(t,x,y)在(t,x,y) ∈[0,T]×[0,M]2上为一致收敛的序列，其中T, M 为任意的正常数.

由上述引理，函数序列{un(t,x,y)}在(t,x,y)∈[0,T]×[0,M]上存在一个极限函数

因此有如下定理.

定理1二维尘埃等离子体低频振动广义非线性扰动KP 方程(16)，当f(u)为低频尘埃声波的扰动项是关于其变量为充分光滑的有界函数时，由(26)决定的极限函数u(t,x,y)是尘埃等离子体低频振动非线性广义扰动KP 方程(16)的精确解.

4 例子

现来考虑一个简单的无量刚尘埃等离子体低频振动非线性广义扰动KP 方程例子.设a=b=c=1，而扰动项为f(u)=exp[−u2].

由式(16)，尘埃等离子体非线性广义扰动KP 程为

作行波变换s=k1x+k2y −t，由式(17)，广义扰动KP 方程(26)为

这里ki(i=1,2,3)由式(12),(13)决定.

用前述变分迭代关系式(24).选取初始近似u0(s)为方程(1)的孤立子波解.即由(14)式得

由式(28)和(24)，可得非线性广义扰动KP 方程(27)解u(s)的一次近似

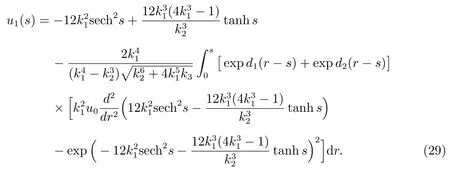
再由(28),(24)式，可求出扰动非线性广义扰动KP 方程(26)解u(s)的二次近似

这里ki, di由式(12),(13),(23)决定，u1由式(29)表示.

继续利用迭代式(24)，可得到尘埃等离子体低频振动非线性广义扰动KP 方程(26)解u(s)的更高的n(n=3,4,···)次近似un(s).

再继续由行波变换(2)，可得到广义扰动KP 方程(16)的第n 近似的孤立子波行波解un(t,x,y)=un(k1x+k2y −t)(n=0,1,2,···).

就是尘埃等离子体低频振动非线性广义KP 方程(27)的精确解.

5 结语

变分迭代理论和方法是通过求泛函的极值来得到对应的Lagrange 乘子.选择适当的初始近似以后，能得到较高精度的近似解.由本文求得的是广义扰动KP 方程尘埃等离子体的低频振动孤立子波的近似解析解.它还可进行解析运算求出相关物理性态，如通过得到的孤立子波波峰值，并采取适当的措施避免“共振”现象而出现电荷超高密度的聚集而导致放电击穿现象等等.关于这方面的进一步的情形，本文不再继续研究.