基于修理设备可更换和修理延迟策略的两不同型部件冷贮备可修系统
2020-09-05魏瑛源唐应辉
魏瑛源, 唐应辉
(1- 河西学院数学与统计学院,甘肃张掖 734000; 2- 四川师范大学数学科学学院,成都 610068)
1 引言
冷贮备可修系统的研究中,已有文献通常都假定修理设备是完全可靠的.事实上,由于磨损和老化等情况,在修理故障部件的过程中,修理设备也可能会发生失效,此时需要被更换后再继续工作.另外,部件发生故障后,要先判断故障原因,或者修理工不在岗(休假或去做辅助性工作),使得故障部件不可能立即得到修理.基于这样的实际情况,文献[1–12]把“修理有延迟”或“修理设备可发生失效且可更换”的策略引入到可修系统的研究中,这是一类更一般的可修系统,既有实际应用背景,又有理论分析意义.
文献[13]在假定部件的工作寿命、故障部件的修理时间和修理延迟时间都具有概率密度函数的条件下(这个假定条件较苛刻),研究了修理有延迟的两个不同型部件组成的冷贮备可修系统,得到了系统首次故障前时间和系统的可用度等可靠性指标.文献[14]研究了修理设备可更换的两个不同型部件组成的冷贮备可修系统,得到了系统和修理设备的一些可靠性指标.正是在这些文献研究的综合启发下,本文讨论修理设备可更换且修理有延迟的冷贮备可修系统,其中故障部件的修理时间和修理延迟时间、修理设备失效后的更换时间都服从任意分布(不一定是连续型),摆脱了对一般连续型分布的依赖性,从模型方面极大地推广了已有文献的研究,使得研究的系统更具一般性,其分析也更复杂.我们使用Markov 更新过程理论、全概率分解技术、L 变换和LS 变换,给出了系统和修理设备的可靠性指标的表达式.系统的描述如下:
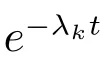
1) 在系统正常工作期间,修理设备处于冷关闭状态,不发生失效;
2) 工作部件发生故障时,贮备部件立即去替换而转为工作状态,转换开关是完全可靠的,状态转换是瞬时完成的;
3) 当一个部件故障时,若修理设备处于关闭状态,则该部件的修理有延迟;在先故障部件的修理延迟时间内或修理时间内故障的部件,其修理没有延迟,但是需要等待先故障部件修复好后再接受修理;
4) 当修理设备失效时,正在接受修理的部件需等待其更换后再继续接受修理,修理设备更换后立即转为工作状态,部件已修理过的时间依然有效;
5) 当部件被修复好后,若此时系统中无待修部件,则修理设备自行关闭,否则,接着修理待修部件;
6) 修复好的部件,或进入冷贮备状态(若此时另一个部件正在工作),或立即进入工作状态(若此时另一个部件已故障);
7) 故障部件被修复好后,完全恢复其功能;
8) Xk, Yk, Wk, U, V, k =1,2 相互独立.

其中
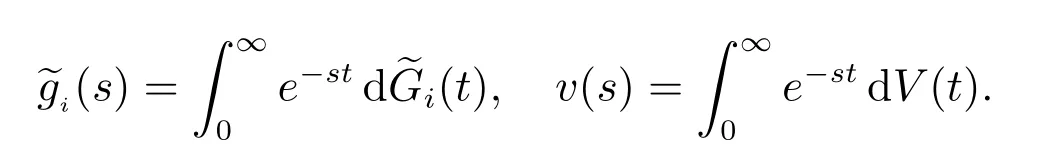
注1本文一律用g(s)和g∗(s)分别表示G(t)的Laplace-Stieltjes 变换(简称LS 变换)和Laplace 变换(简称L 变换),即
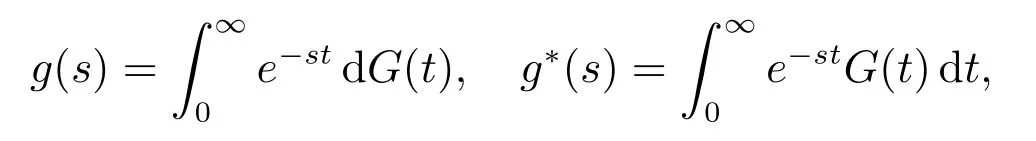
G(k)(t)表示G(t)的k 重卷积,且G(0)(t)=1, t ≥0;Z0表示t=0 时系统的状态;ℜ(s)表示复变数s 的实部.
2 更新过程
系统的状态定义为:状态0(1)表示部件1(2)正在工作,部件2(1)开始冷贮备;状态2(3)表示部件2(1)正在工作,部件1(2)开始修理延迟;状态4(5)表示部件2(1)正在工作,部件1(2)开始被修理;状态6(7)表示部件2(1)正在待修,部件1(2)开始被修理.
用Z(t) = j 表示系统在时刻t 处于状态j, j = 0,1,··· ,7.由负指数分布的无记忆性可知,进入状态0,1,··· ,7 的时刻都是系统的再生点.用Tn表示系统第n 次发生状态转移的时刻,T0= 0;令Zn= Z(Tn+0)表示系统在第n 次状态转移时所进入的状态.容易验证,{Zn, Tn; n=0,1,···}是一个状态空间为E ={0,1,··· ,7}的齐次Markov 更新过程,{Z(t), t ≥0}是一个齐次半Markov 过程.由半Markov 核的定义
Qij(t)=P{Zn+1=j, Tn+1−Tn≤t|Zn=i}, i,j =0,1,··· ,7, n=0,1,··· ,
可以计算出所有半Markov 核为

为下面讨论问题方便,引进四个虚设状态:
状态8(9):部件1(2)正处于修理延迟,部件2(1)开始待修;
状态10(11):部件1(2)正在被修理,部件2(1)开始待修.
由于故障部件的修理延迟时间和修理时间均服从任意分布,因而进入状态8, 9, 10, 11的时刻不是系统的再生点.显然状态6,7,··· ,11 都是系统的故障状态,且
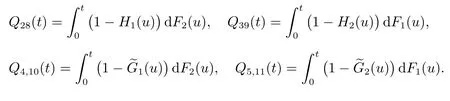
对以上各式作LS 变换,并记
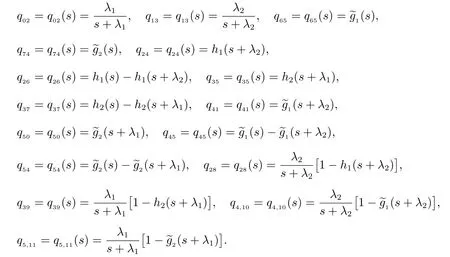
另外,记

3 系统的可靠性指标
3.1 系统首次故障前时间的分布
令

如果一个可修系统一旦发生故障将产生灾难性后果,那么系统首次故障前时间的分布及其均值是该系统最重要的可靠性数量指标.另外,根据Ψi(t),能得到系统在时刻t 以前都正常的概率为1 −Ψi(t) = P{δ > t|Z0= i},这也是可修系统在时间区间(0,t]内不故障的概率.
定理1对ℜ(s)>0,Ψi(t)的LS 变换为

其中

且系统首次故障前的平均时间为
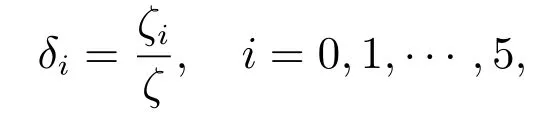
其中
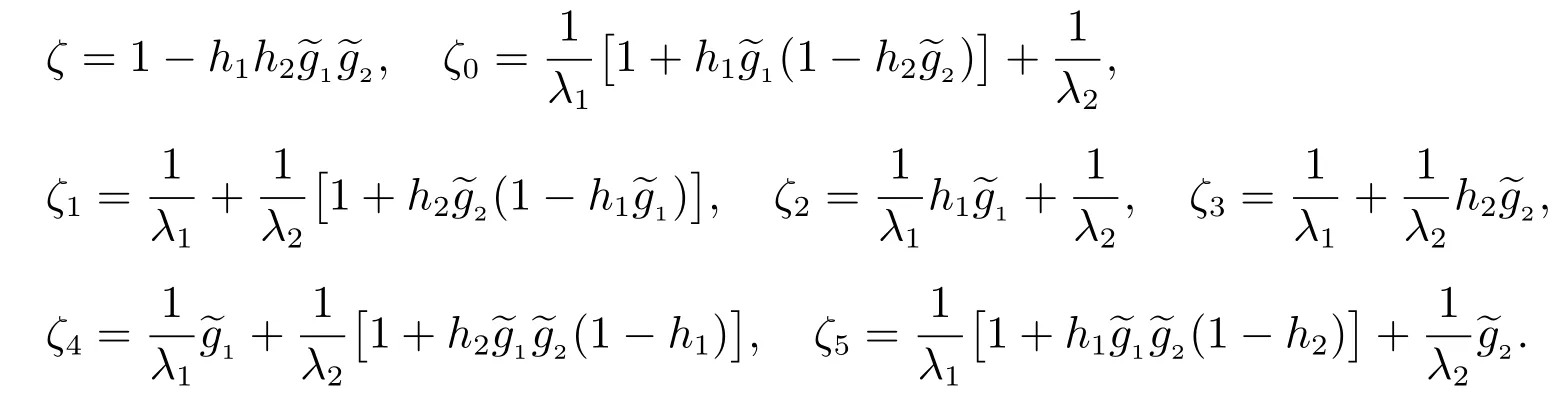
证明 由Ψ2(t)的定义及系统状态的转移关系,得
Ψ2(t)=P{δ ≤t,T1≤t|Z0=2}+P{δ ≤t,T1>t|Z0=2}
=Q24(t)∗Ψ4(t)+Q28(t).
类似地,可得
Ψ0(t)=Q02(t)∗Ψ2(t), Ψ1(t)=Q13(t)∗Ψ3(t), Ψ3(t)=Q35(t)∗Ψ5(t)+Q39(t),
Ψ4(t)=Q41(t)∗Ψ1(t)+Q4,10(t), Ψ5(t)=Q50(t)∗Ψ0(t)+Q5,11(t).
对各式两端作LS 变换,可得(1)式.再由

可得系统首次故障前平均时间.
3.2 系统的可用度
对t ≥0,令

定理2对ℜ(s)>0,Ai(t)的L 变换为

其中
η(s)=(1 −q41q13q37q74)(1 −q50q02q26q65)−(q41q13q35+q45)(q50q02q24+q54),
η0(s)=q02η2(s)+e0η(s), η1(s)=q13η3(s)+e1η(s),
η2(s)=(q24+q26q65q54)(e1+q41q13e3)+(q41q13q35+q45)(q24e0−q54e2)+(1 −q41q13q37q74)(q26q65e0+e2),
η3(s)=(q35+q37q74q45)(e0+q50q02e2)+(q50q02q24+q54)(q35e1−q45e3)+(1 −q50q02q26q65)(q37q74e1+e3),
η4(s)=(q41q13q35+q45)(e0+q50q02e2)+(1 −q50q02q26q65)(e1+q41q13e3),
η5(s)=(1 −q41q13q37q74)(e0+q50q02e2)+(q50q02q24+q54)(e1+q41q13e3),
η6(s)=q65η5(s), η7(s)=q74η4(s),
且系统的稳态可用度为

与初始状态i 无关,i ∈E,其中
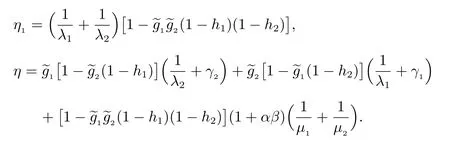

证明 令则由Ai(t)的定义及系统状态的转移关系,得
A2(t)=P{X(t)=1,T1≤t|Z0=2}+P{X(t)=1,T1>t|Z0=2}
=Q24(t)∗A4(t)+Q26(t)∗A6(t)+1 −Q24(t)−Q26(t).
类似地,可得
A0(t)=Q02(t)∗A2(t)+1 −Q02(t), A1(t)=Q13(t)∗A3(t)+1 −Q13(t),
A3(t)=Q35(t)∗A5(t)+Q37(t)∗A7(t)+1 −Q35(t)−Q39(t),
A4(t)=Q41(t)∗A1(t)+Q45(t)∗A5(t)+1 −Q41(t)−Q4,10(t),
A5(t)=Q50(t)∗A0(t)+Q54(t)∗A4(t)+1 −Q50(t)−Q5,11(t),
A6(t)=Q65(t)∗A5(t), A7(t)=Q74(t)∗A4(t).
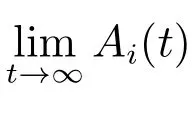

于是再使用L’Hospital 法则,可得(3)式.
3.3 系统在有限区间(0,t]内发生故障的平均次数
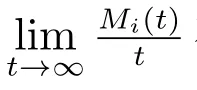
定理3对ℜ(s)>0,Mi(t)的LS 变换为

其中
ρ0(s)=q02ρ2(s), ρ1(s)=q13ρ3(s), ρ6(s)=q65ρ5(s), ρ7(s)=q74ρ4(s),
ρ2(s)=(q41q13q35+q45)(q24q5,11−q28q54)+(q41q13q39+q4,10)(q24+q26q65q54)+(1 −q41q13q37q74)(q26q65q5,11+q28),
ρ3(s)=(q50q02q24+q54)(q35q4,10−q39q45)+(q50q02q28+q5,11)(q35+q37q74q45)+(1 −q50q02q26q65)(q37q74q4,10+q39),
ρ4(s)=(q41q13q35+q45)(q50q02q28+q5,11)+(1 −q50q02q26q65)(q41q13q39+q4,10),ρ5(s)=(q50q02q24+q54)(q41q13q39+q4,10)+(1 −q41q13q37q74)(q50q02q28+q5,11),
且系统的稳态故障频度为

与初始状态i 无关,i ∈E,其中η 由定理2 给出,
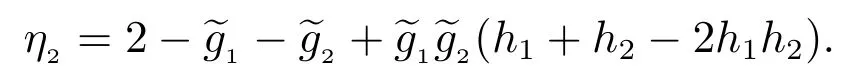
证明 类似于定理2 的证明.
3.4 系统在时刻t 等待修理的概率
系统在时刻t 等待修理是指在时刻t 两部件都故障,且都没有被修理.因此,考察时刻0 系统由状态i 出发,在时刻t 等待修理的概率,可进一步明确系统的不可用度.对t ≥0,令
Di(t)=P{系统在时刻t 等待修理|Z0=i}, i ∈E.
定理4对ℜ(s)>0,Di(t)的L 变换为

其中
ξ0(s)=q02ξ2(s), ξ1(s)=q13ξ3(s), ξ6(s)=q65ξ5(s), ξ7(s)=q74ξ4(s),
ξ2(s)=(q24+q26q65q54)q41q13(q39−q37)+(q28q26)(1 −q41q13q37q74−q41q13q35q54−q45q54),
ξ3(s)=(q35+q37q74q45)q50q02(q28−q26)+(q39q37)(1 −q50q02q26q65−q50q02q24q45−q54q45),
ξ4(s)=(q41q13q35+q45)q50q02(q28−q26)+(1 −q50q02q26q65)q41q13(q39−q37),
ξ5(s)=(q50q02q24+q54)q41q13(q39−q37)+(1 −q41q13q37q74)q50q02(q28−q26),
且稳态概率为

与初始状态i 无关,i ∈E,其中η 由定理2 给出,

证明 类似于定理2 的证明.
3.5 修理延迟时间对δ0, A0 的影响分析
讨论修理延迟时间的改变对系统首次故障前平均时间和系统的稳态可用度的影响程度.假设:
(i) 部件1 和部件2 是两个同型部件,寿命服从参数为λ 的负指数分布;
(ii) α=0,即修理设备完全可靠,不发生失效;
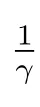
(iv) 部件故障后的修理时间服从参数为µ的负指数分布;
(v) Z0=0,即时刻0 系统从状态0(部件1 在工作,部件2 开始冷贮备)开始.
用δ0和A0分别表示系统首次故障前平均时间和系统的稳态可用度.


表1: µ和γ(γ =)的不同值所对应的δAd 的值

表1: µ和γ(γ =)的不同值所对应的δAd 的值
µγ 0.1 0.2 0.5 1.0 2.0 5.0 10.0 20.0 0.05 0.5344 0.1 0.9957 0.9949 0.9860 0.9697 0.9348 0.8352 0.7043 0.3842 0.2 0.9953 0.9903 0.9739 0.9444 0.8846 0.7321 0.5635 0.2657 0.5 0.9914 0.9824 0.9538 0.9048 0.8125 0.6104 0.4271 0.1700 1.0 0.9831 0.9659 0.9143 0.8334 0.7000 0.4643 0.2949 0.1322 2.0 0.9751 0.9504 0.8800 0.7778 0.6250 0.3878 0.2361 0.1120 5.0 0.9673 0.9358 0.9860 0.7333 0.5714 0.3407 0.2029 0.0995 10.0 0.9597 0.9221 0.9860 0.6970 0.5313 0.3088 0.1815 0.0952 20.0 0.9563 0.9161 0.9860 0.6825 0.5161 0.2974 0.1742 0.9545 0.9127 0.9860 0.6748 0.5082 0.2916 0.1704 0.0931
表2: µ和γ(γ =)的不同值所对应的AAd 的值

表2: µ和γ(γ =)的不同值所对应的AAd 的值
µγ 0.1 0.2 0.5 1.0 2.0 5.0 10.0 20.0 0.05 0.9958 0.1 0.9996 0.9987 0.9952 0.9915 0.9900 0.9921 0.9942 0.9884 0.2 0.9992 0.9973 0.9904 0.9829 0.9792 0.9822 0.9858 0.9673 0.5 0.9984 0.9946 0.9808 0.9653 0.9563 0.9585 0.9635 0.8837 1.0 0.9959 0.9866 0.9524 0.9130 0.8851 0.8770 0.8801 0.7479 2.0 0.9918 0.9734 0.9074 0.8333 0.7778 0.7507 0.7475 0.5576 5.0 0.9838 0.9480 0.8280 0.7059 0.6195 0.5718 0.5612 0.3098 10.0 0.9604 0.8790 0.6545 0.4811 0.3798 0.3280 0.3150 0.1769 20.0 0.9238 0.7838 0.4847 0.3137 0.2303 0.1908 0.1810 0.8583 0.6442 0.3131 0.1849 0.1287 0.1038 0.0977 0.0951
3.6 修理设备的失效率和更换率对系统可靠性指标的影响分析

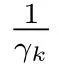
取λ1= 0.2, λ2= 0.5, µ1= 2, µ2= 1, γ1= 3, γ2= 5,图1 至图4 给出了以α 为自变量的δ0, A0, M 和D 的变化图形,四条曲线分别对应于β =0.1, β = 1, β =2, β =5.从图1 至图4 可以看出,δ0, A0, M 和D 随着α 的增大而减小,并逐渐趋于稳定值;另外,当修理设备失效后的平均更换时间β 越来越短时,δ0, A0,M 和D 有所增大.
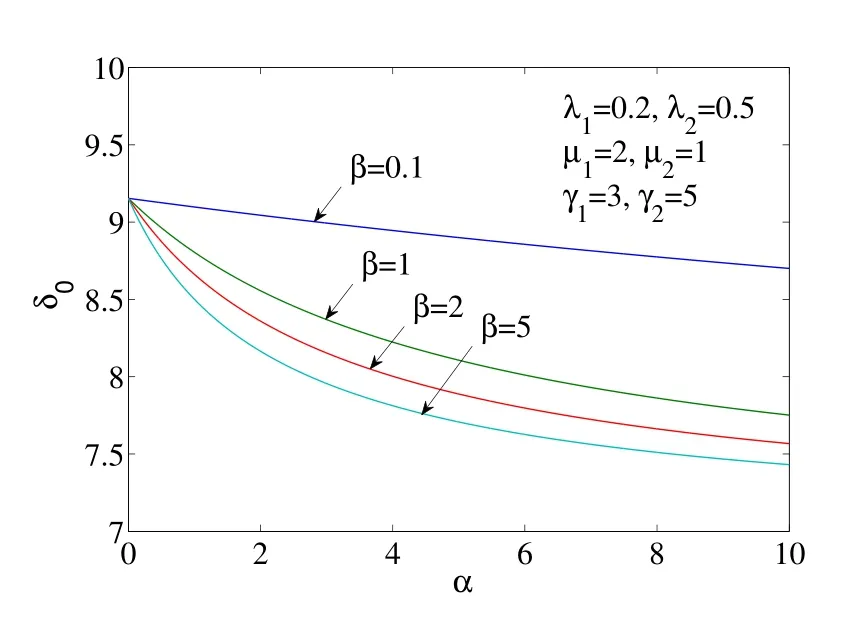
图1: 以α 为自变量的δ0 的图形
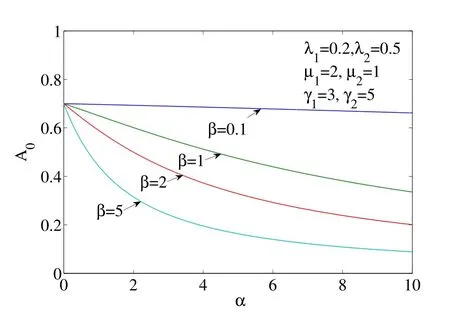
图2: 以α 为自变量的A0 的图形

图3: 以α 为自变量的M 的图形
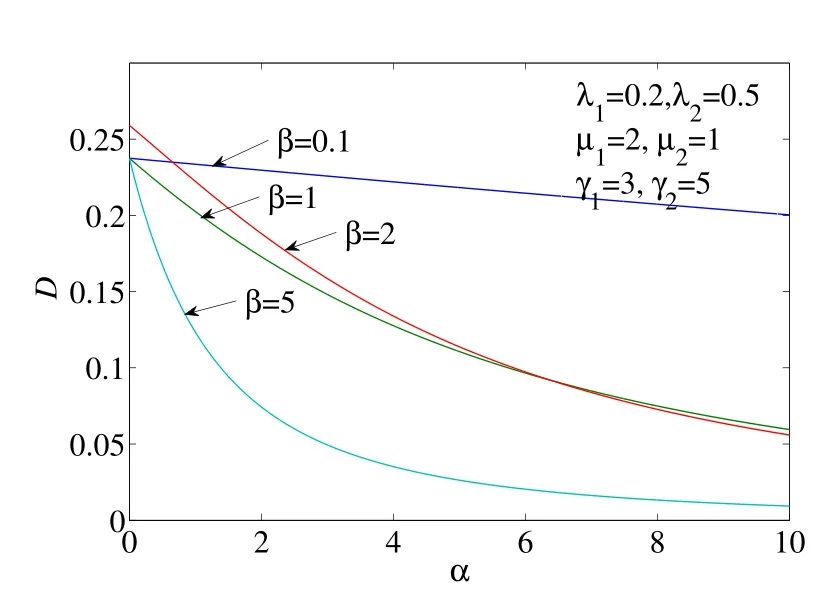
图4: 以α 为自变量的D 的图形
4 修理设备的可靠性指标
4.1 修理设备的闲期和“广义忙期”

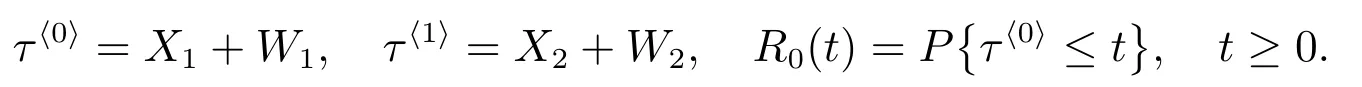
定理5对ℜ(s)>0,则R(t)和R0(t)的LS 变换为

且修理设备闲期的平均长度为

其中


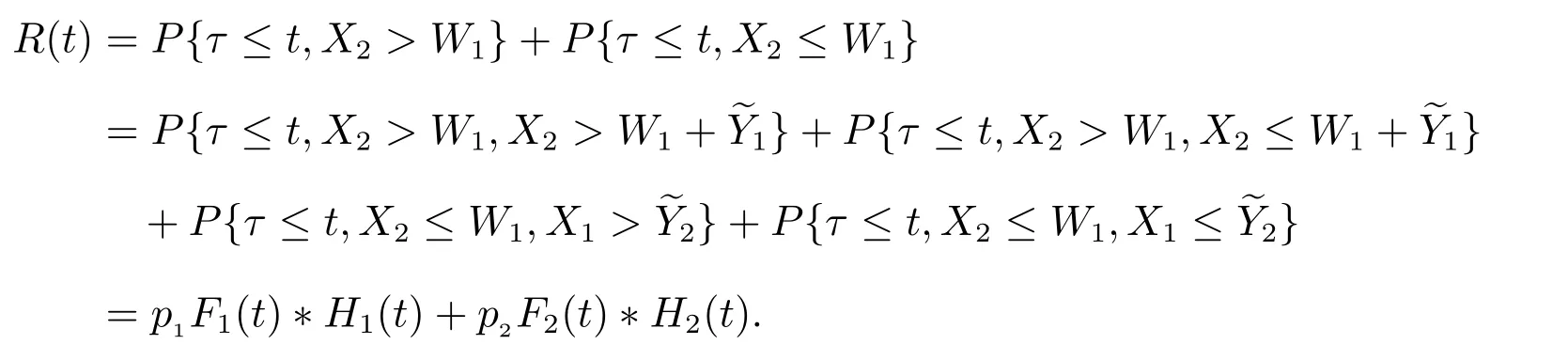
对上式作LS 变换,可得(8)式.再由

可得修理设备闲期的平均长度.
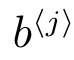

且
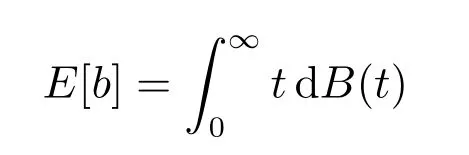
为“广义忙期”的平均长度.
修理设备的“广义忙期”这段时间是修理设备连续繁忙的时间,它反映了系统中修理设备的工作强度.均值E[b]表示系统经过长期运行,大约有E[b]长的时间修理设备是繁忙的,它是反映修理能力的配备是否合理的一个数量指标.
定理6对ℜ(s)>0,则B(t)的LS 变换为

且“广义忙期”的平均长度为

其中p1, p2由定理5 给出,

证明
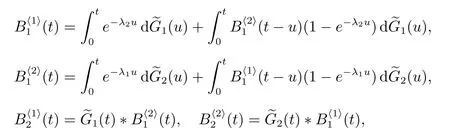
从而得

类似于定理5 的证明,可得
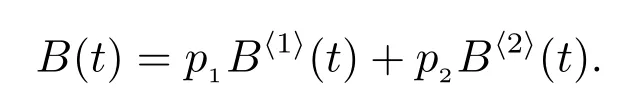
作LS 变换,得(9)式.再由

得(10)式.
对t ≥0,令

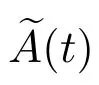

且稳态概率为
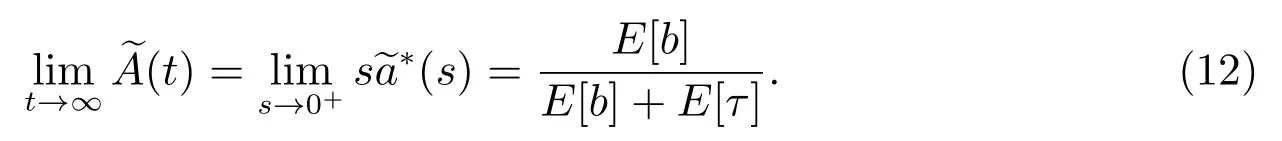
证明 根据模型的描述,修理设备的闲期与“广义忙期”构成一个延迟交替更新过程,故根据延迟交替更新过程理论[16,17]可得.
4.2 修理设备的不可用度
由单部件组成的可修系统是最简单的可修系统,当部件工作时系统工作,当部件故障时系统故障.假设部件的寿命U 服从参数为α 的负指数分布U(t) = 1 −e−αt, t ≥0,部件故障后立即被修理,其修理时间V 服从任意分布V(t), t ≥0,平均修理时间为β.部件修复好后,其寿命与新部件相同,并立即进入工作状态,进一步假设时刻0 部件是新的,且U 与V 相互独立.对t ≥0,令

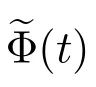
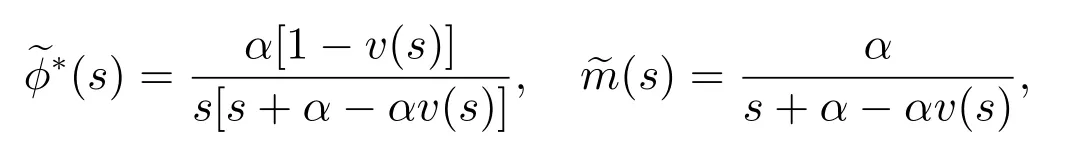
而且有稳态结果

下面,我们讨论修理设备在时刻t 发生失效且处于更换状态的概率,即修理设备的不可用度.
对t ≥0,令
Φ(t)=P{修理设备在时刻t 发生失效且处于更换状态}.
定理8对ℜ(s)>0,Φ(t)的L 变换为

且稳态概率为

证明 1) 令τj, bj分别表示修理设备的第j 个闲期与第j 个“广义忙期”,j =1,2,···.根据模型的描述,修理设备在其闲期内是不会发生失效的,而且在每个“广义忙期”开始的时刻和结束的时刻都正常,其寿命仍然为U,所以修理设备在时刻t 发生失效且处于更换状态,当且仅当时刻t 落入某个“广义忙期”中,并且修理设备在时刻t 发生失效,从而有
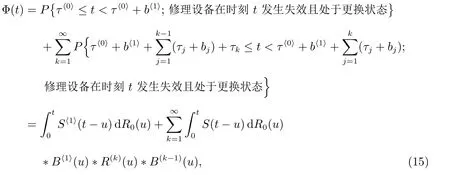
其中

S(t)=P{0 ≤t 2) 对t ≥0,有 定理9令K 表示在“广义忙期”内修理设备修复好的故障部件数,则其概率分布函数为 且均值为 根据 定理得证. 定理10对ℜ(s)>0,M(t)的LS 变换为 且稳态更换频度为 证明 1) 令 则有 2) 因为修理设备仅在“广义忙期”中发生失效,所以 对各式两端分别作LS 变换,整理可得(17)式. 本文在由两个不同型部件组成的冷贮备可修系统中,考虑了“修理有延迟”和“修理设备在修理故障部件的过程中可能发生失效而需要被更换”的策略,使得推广的模型更符合实际应用背景.利用Markov 更新过程理论,得到了一些可靠性指标,并且通过数值实例分析了修理延迟时间和修理设备的失效率对相关指标的影响,使得所得的理论结果有更清晰的应用意义. 致谢:本文作者对审稿人表示衷心感谢!
4.3 在广义忙期内修理设备修复好的故障部件数

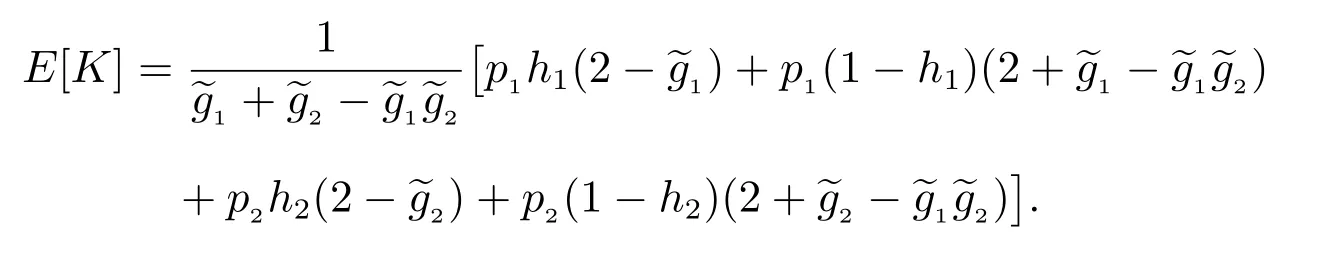
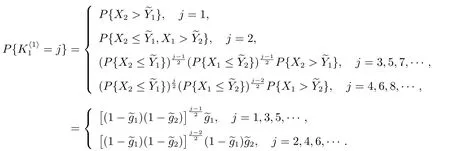
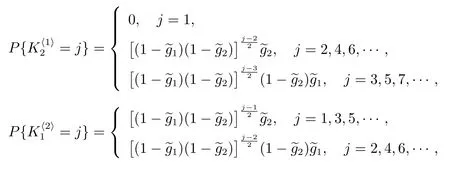

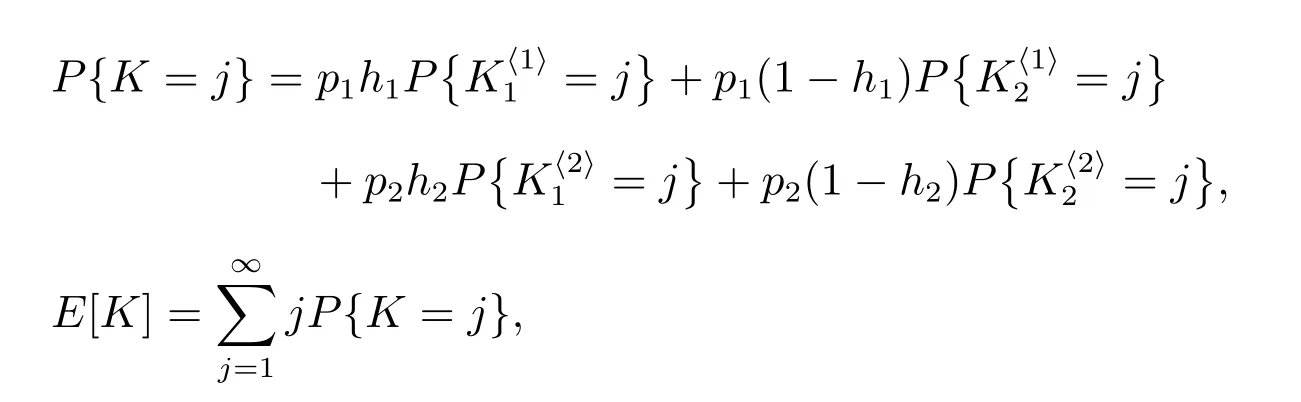
4.4 修理设备发生失效所需的更换次数
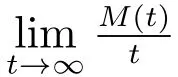



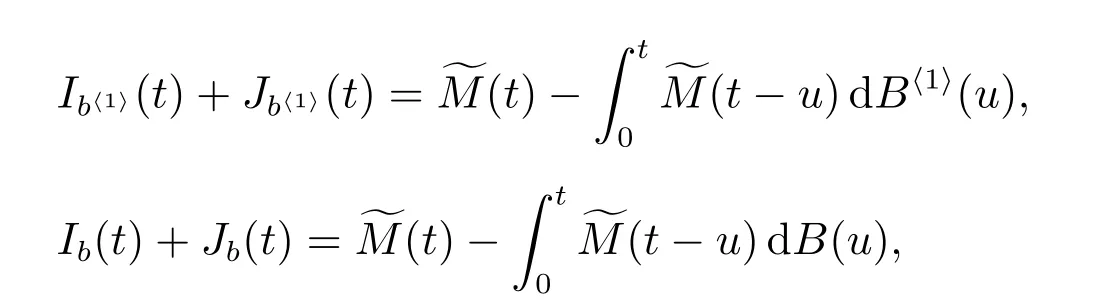
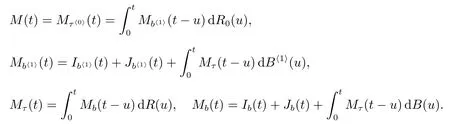
5 结论
