基于加速度信号的吊弦断裂检测方法

聂晶鑫

(中铁第一勘察设计院集团有限公司，西安 710043)

1 引言

接触网的工作状态直接关系着列车的运行安全.接触网沿线路露天架设，长期受环境、气候等自然因素以及车辆受电弓的冲击作用，容易发生故障[1].吊弦是接触网的关键部件，起着固定接触线的作用.当列车行驶时，受电弓作用于接触线，引起吊弦和承力索的舞动.这种方式日复一日地运行，在交变应力作用下可能发生吊弦断裂事故，威胁行车安全，如武广线在2011 年发现吊弦断裂问题多达60 处[2].因此，对吊弦进行在线监测，及时发现吊弦故障，是保障接触网安全的有力措施.

近年来，国内外针对接触网运行状态，研究了基于多种技术的检测方法，总体来说，可分为接触式及非接触式检测方法.非接触式方法通过图像识别技术从外观上发现吊弦故障.文献[3]以4C 巡检高清图像为对象，基于卷积神经网络实现接触网七种关键区域(包括吊弦)的缺陷检测，但这种方法的检测精度有限，容易出现误报和漏报.于是人们开始研究接触式检测方法.文献[1]从接触网—受电弓的耦合动力学角度出发，分析了不同接触网结构故障的动力学响应特征，运用支持向量机进行故障特征识别.文献[4]基于混合滤波器对含噪信号进行消噪处理，对信号进行小波变换，根据模极大值原理计算Lipschitz 指数，实现断线故障的检测.但是这些方法故障识别率有待进一步提高.

本文建立兰新高速铁路弓网动态仿真模型[5]，通过有限元方法对模型进行求解，获取在脉动风和受电弓同时作用下的接触网正常和发生故障时接触线和承力索监测点的加速度数据，然后运用EEMD 提取加速度信号的多种特征，建立吊弦断裂故障诊断L1/2-LR 模型.实验结果表明，所建立的检测模型，在脉动风和受电弓共同作用工况下准确率达到97.25%.

2 数据仿真

2.1 仿真模型

本文对兰新高铁里程为K3066+568.795 ∼K3065+588.795 的接触网试验段建立弓网动态仿真模型[5].受电弓的仿真使用三归算质量-阻尼-刚度模型，接触网的相关设计参数如表1 所示.

表1: 接触网设计参数

2.2 传感器安装

接触网每跨长度为50 米，共有9 个吊弦，每隔5 米在承力索和接触线之间安装有1 根吊弦.通过在接触网上安装加速度传感器提取两种工况下的接触网力学响应，加速度传感器的安装位置如图1 所示.

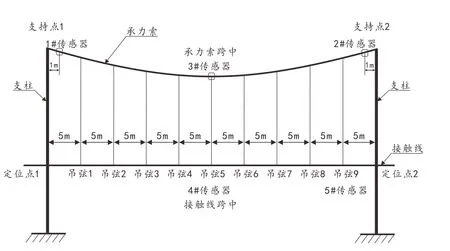
图1: 接触网力学性能响应数据提取点

1#加速度传感器：承力索上支持点1 内侧1m 处；

2#加速度传感器：承力索上支持点2 内侧1m 处；

3#加速度传感器：承力索上跨中位置；

4#加速度传感器：接触线上跨中吊弦5 处；

5#加速度传感器：接触线上跨中吊弦9 处.

2.3 仿真工况

为获取1#∼5#检测点的加速度，本文对列车以250 km/h 的速度行驶时，接触网试验段受电弓和脉动风同时作用下，吊弦无断裂和21 跨的跨中位置吊弦断裂两种工况进行仿真，获取了400 组数据，其中包括两种工况各200 组.加速度传感器的采样频率为277 Hz，每条样本采集时间为17 秒，共4800 个数据点.每组数据包括5 个加速度传感器所采集的垂直、水平方向振动加速度.

3 基于EEMD 分解的特征提取

通过对脉动风和受电弓同时作用下，跨中吊弦断裂及没有断裂情况下的加速度信号进行分析，发现传感器采集的加速度信号数据是非线性非平稳的，所以需要采用EEMD 方法，将原始信号数据分解为多个本征模态函数，再提取本征模态函数的能量熵、平均熵和奇异熵特征.

3.1 EEMD 分解

经验模态分解方法(EMD)[6]将一个频率不规则的波化为多个单一频率的波加残波的形式，单一频率的波称为本征模态函数(IMF)，但EMD 存在模态混叠缺陷.为了克服这一问题，本文采用EEMD[7]进行加速度信号特征提取.EEMD 分解以EMD 理论为基础，在原始信号中多次添加白噪声.因为白噪声具有均匀频率分布特性，可以改变信号中极值点分布，有利于信号的抗混分解，有效地抑制了模式混淆.其分解步骤见算法1.

算法1EEMD 分解

输入：原始信号

输出：多次分解下的平均IMF

步骤3：获得多次分解下的平均IMF，以消除各分量重残余的白噪声

其中cj(t)为对原始信号进行EEMD 分解后所得的第j 个IMF.

3.2 信息熵特征

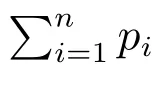
将EEMD 和信息熵结合，能达到信息融合的目的，可有效地分析信号中的突变情况.这里主要采用IMF 的三种熵测度，即IMF 能量熵、IMF 奇异熵和IMF 平均熵[8].

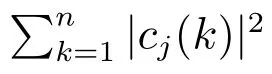
1) 能量熵的计算

2) IMF 奇异熵

表示第j 个IMF 分量的奇异熵，则整个信号的奇异熵定义为

IMF 奇异熵反映信号经EEMD 分解出的尺度空间中IMF 分量能量的分布的不确定性.如果信号比较简单，能量就集中在少数几个IMF 分量上，奇异熵就越小；如果信号比较复杂，能量就越分散，奇异熵就越大.

3) 平均熵的计算

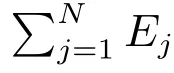
IMF 平均熵体现信号在IMF 分量上的平均复杂度，与时间、频率变化无关.能量分布越是均匀，平均熵就越大.

3.3 特征提取

加速度信号经过EEMD，形成多个本征函数IMF，计算各IMF 与原始信号的皮尔逊相关系数，挑选出有效的IMF 分量.本文设置阈值为0.1，即取皮氏积矩相关系数大于0.1 的IMF 分量作为有效分量来计算IMF 熵特征.

设X 和Y 为两个向量，xi,yi(i = 1,2,··· ,N)为各自的分量，其皮氏积矩相关系数r 计算公式为

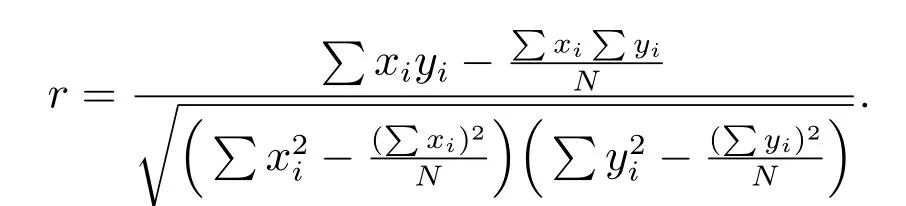
应用算法1，加速度信号经过EEMD 分解为12 个IMF 分量.在受电弓和脉动风同时作用下，各个加速度的IMF7–IMF12 分量和原信号的相关系数都小于0.1，可以忽略.因此选取经EEMD 分解后的1 ∼6 的IMF 分量.承力索支持点1 垂直加速度、承力索跨中垂直加速度、承力索支持点2 垂直加速度、承力索支持点1 水平加速度、承力索跨中水平加速度和承力索支持点2 水平加速度的IMF1–IMF6 分量与原信号的相关系数见表2.

表2: IMF 分量与分解前信号的相关系数

选取1#∼5#传感器的10 个加速度信号的1 ∼6 的IMF 分量，计算其IMF 能量熵、IMF 奇异熵、IMF 平均熵，共30 个特征.

4 吊弦断裂检测L1/2-LR 模型

通过EEMD 分解提取的30 特征可能存在冗余的变量，所以需要进行特征选择，找到对故障识别具有显著影响的变量进行故障诊断.本文结合L1/2正则化很强的稀疏性和Logistic 回归良好的分类性能，建立L1/2-LR[9-12]吊弦断裂检测模型.

4.1 L1/2-LR 模型

L1/2-LR 正则化优化模型如下

其中p 为向量x的维数，N 为样本个数，xi=(xi1,xi2,··· ,xip)为第i 个样本的属性向量，yi为样本xi的标号，取值为−1 或1，分别代表样本xi发生吊弦断裂和未发生吊弦断裂，w =(w0,w1,w2,··· ,wp)为待求未知向量，λ>0 为正则化常数.

4.2 L1/2-LR 模型求解算法

L1/2-LR 分类模型是一种非凸优化模型，可应用阈值迭代算法求解.

算法2L1/2-LR 的阈值迭代算法

输出：分类判别函数

步骤1：初始化w0=(0,0,··· ,0)T，训练步数t=0；

步骤2：按公式

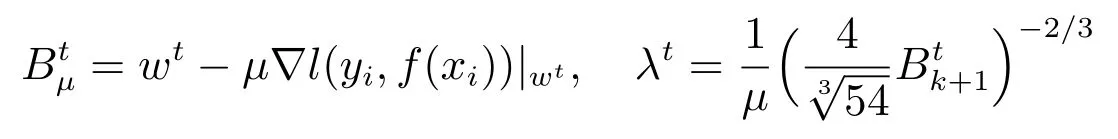
步骤3：令λ=λt，更新wt+1=Hλµ(Btµ)，其中

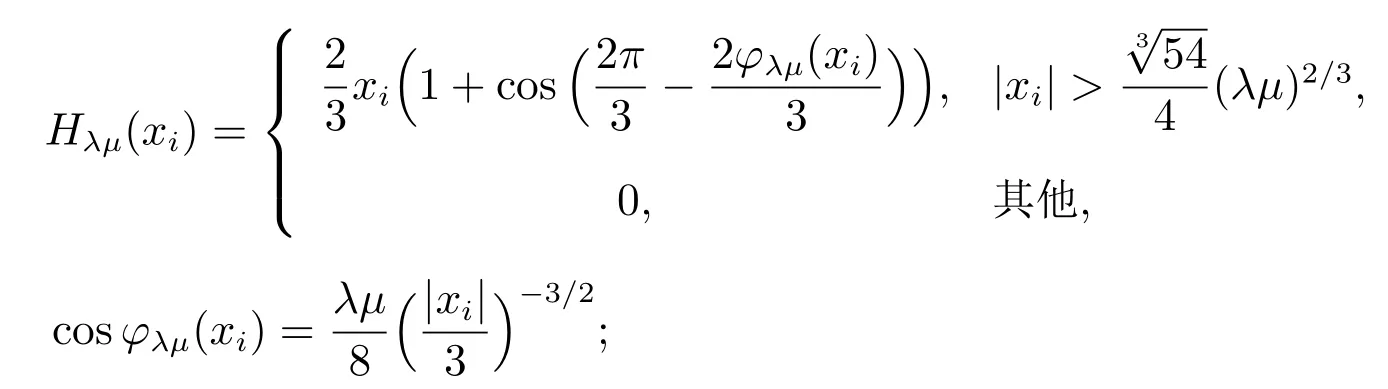
4.3 L1/2-LR 模型求解

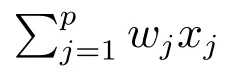
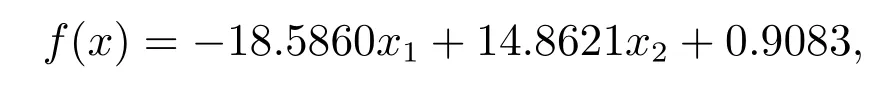
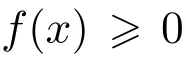
5 结论

本文提出了一种基于加速度信号EEMD 的接触网吊弦断裂检测方法.本方法通过对接触网承力索和接触线上采样点的加速度信号进行EEMD 分解、计算本征模态函数，对其提取能量熵、平均熵和奇异熵，以这三种类型的熵特征建立了吊弦断裂检测L1/2-LR 模型.实验表明，在脉动风和受电弓同时作用的工况下，所得到的检测方法对吊弦断裂检测的准确率可达97.25%.本文提出的L1/2-LR 模型，具有变量选择作用，发现只需采集承力索跨中位置处的垂直加速度和中水平加速度，分别计算其能量熵、平均熵，就可以以很高的精度和计算效率检测跨中吊弦是否断裂.