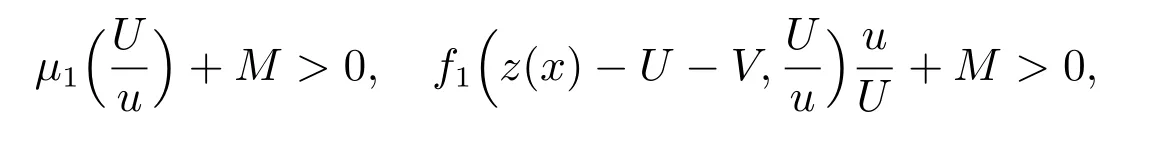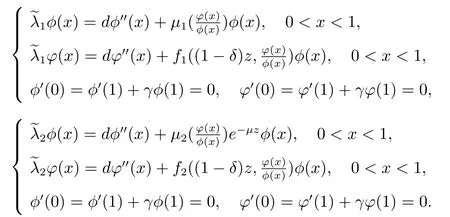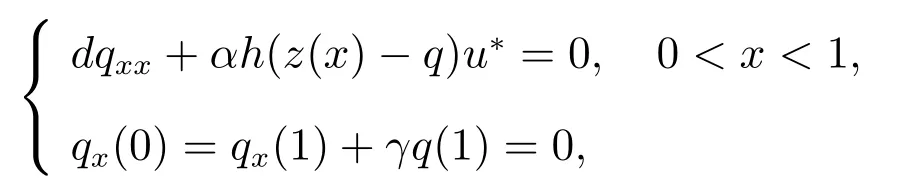一类具有内部存储和外部抑制剂的非均匀恒化器模型

2020-09-05李双妃王治国

工程数学学报 2020年4期

李双妃, 王治国, 曹毅

(陕西师范大学数学与信息科学学院，西安 710119)

1 引言

经典的恒化器模型通常假设营养吸收率与微生物的增长率成正比，因此被称为常数产出模型.然而，Ketchum[1]在实验中发现，在外部的营养物质耗尽后，藻类种群仍旧可以存活数周.这意味着，要恰当地描述生物的生长，应当将内部营养水平视为变量.因此，Droop[2,3]提出了带有内部存储的浮游植物生长模型.考虑到空间扩散的作用，Hsu 等[4,5]研究了一类带有内部存储的单资源非均匀恒化器模型.结果表明，存在临界的扩散系数，当扩散系数小于临界扩散系数时，将会出现竞争排斥或共存的现象；反之，两物种均将死亡.Hsu 等[6]考虑了一类带有内部存储的消耗无机碳的双资源非均匀恒化器模型，证明了物种存活时，正平衡解的唯一性及全局吸引性.

在生态学中，抑制剂可以降低某些有害生物的生长率，从而对环境治理具有重要作用.早在1986 年，Lenski 和Hattingh[7]提出了一类具有抑制剂的均匀恒化器模型.Hsu 和Waltman[8]研究了该模型解的一致持续性.Nie 和Wu[9]引入扩散，建立了具有扩散的非均匀恒化器模型，研究了系统的渐近动力学行为以及模型共存解的全局结构和局部稳定性.文献[10]进一步研究了该模型正平衡解的唯一性和稳定性.然而，这些模型均忽略了物种对于营养的吸收存储过程.

基于以上研究结果，本文研究一类具有内部存储和外部抑制剂的恒化器模型.在t 时刻，假设营养物的浓度为S(t)；种群密度为u(t), v(t)；物种i 每个细胞所平均存储的营养为Qi(t)，其中i = 1,2 分别指代u 和v；抑制剂浓度为p(t).这里假设v 为受抑制剂影响的物种，u 为吸收抑制剂的物种.考虑如下均匀恒化器模型

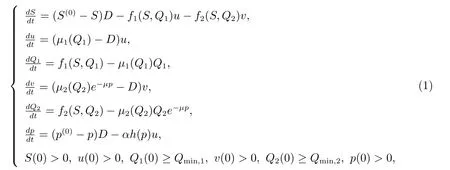
其中S(0)> 0 为营养物的输入浓度，p(0)> 0 为抑制剂的输入浓度，两者均为常数；D 为稀释率；µi(Qi)为物种i 的生长率；fi(S,Qi)为物种i 的营养吸收率；Qmin,i为物种i 的临界细胞份额，即当细胞所存储的营养低于该值时，物种将停止生长；α 为物种u 对抑制剂p 的吸收率；h(p) = p/(h1+p)，其中h1为半饱和常数；函数e−µp为抑制剂p 对物种v 的抑制程度，其中µ>0 为常数.

文献[3,11]中生长率µi(Qi)和吸收率fi(S,Qi)采取如下形式

其中

参考以上例子，对函数µi(Qi)和fi(S,Qi)作如下假设：

µi(Qmin,i)=0;

(H2):

(ii) 当S ≥0, Qi≥Qmin,i时，

fi(S,Qi)≥0 几乎处处成立；

(iii) 存在QBi∈(Qmin,i,+∞]，对任意的(S,Qi) ∈{(S,Qi) ∈R+×[Qmin,i,+∞) :S >0, Qi∈[Qmin,i,QBi)}，有

且当S = 0 或者Qi≥QBi时，fi(S,Qi) = 0.当QBi= +∞时，fi(S,Qi) = 0 当且仅当S =0.

令U = Q1u, V = Q2v 分别表示物种u, v 在t 时刻体内所存储的营养.同时引入扩散，则系统(1)可化为

边界条件和初始条件为

其中初始值函数u0(x), U0(x), v0(x), V0(x)满足

本文主要研究系统(2)–(3)正平衡解的存在性，故考虑相应的平衡态方程.令为节省记号，仍用原记号表示相应的无量纲化参数.因此，系统(2)–(3)可简化为

边界条件为

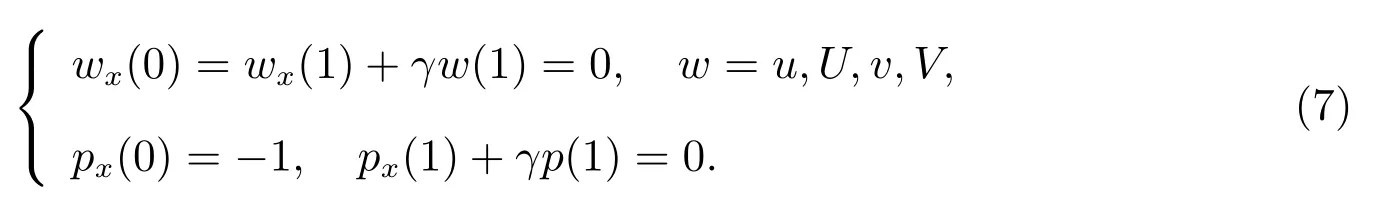
本文主要研究系统(6)–(7)正解的存在性，故对函数µi(Qi), fi(S,Qi)以及h(p)作如下延拓

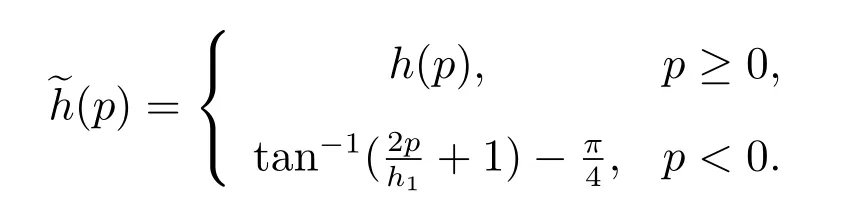
本文首先给出一些基本结果以及系统非负解的先验估计，再利用Amann 的拓扑不动点指标理论计算算子在所有平凡和半平凡不动点邻域内的指标，进而证明系统正平衡解的存在性.最后，需要指出的是在利用拓扑度理论研究系统正平衡解的存在性时，通常在系统各分量均非负的锥上使用拓扑度的不动点理论，如文献[12,13]，但这样的锥对本文模型并不适用，本文将在更小的锥上使用不动点理论.

2 预备知识

首先考虑如下的非线性特征值问题

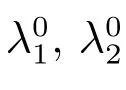
注：对于另一个单物种的平衡态问题

引理2[9]边值问题

有唯一正解，记为p∗，且满足0

(i) u>0, v >0, U >0, V >0, 0

(ii) U +V

(iii) U >uQmin,1, V >vQmin,2;

由文献[6]得

其中

3 正解的存在性

本节运用拓扑度理论研究系统(6)–(7)正解的存在性.令q = z(x) −p，则p =z(x)−q.因此，系统(6)–(7)等价于

边界条件为

引入以下空间

CB[0,1]={u ∈C[0,1]:ux(0)=ux(1)+γu(1)=0}, X =(C[0,1])5,

W3={q ∈C[0,1]:q ≥0}, W =W1×W2×W3,

E ={(u,U,v,V,q)∈W :∥u∥+∥U∥+∥v∥+∥V ∥+∥q∥≤R0, x ∈[0,1]},

∥·∥为最大模范数.

定义F :E →X 如下

其中ξ1, ϑ1分别由(13),(14)给出

引理4对任意的λ ≥1, F(u,U,v,V,q) = λ(u,U,v,V,q)在W 中没有解满足∥u∥+∥U∥+∥v∥+∥V ∥+∥q∥=R0.

证明假设(u,U,v,V,q)∈W 满足F(u,U,v,V,q)=λ(u,U,v,V,q)，且∥u∥+∥U∥+∥v∥+∥V ∥+∥q∥=R0，则有

故F(u,U,v,V,q)=λ(u,U,v,V,q)在W 中没有解满足

∥u∥+∥U∥+∥v∥+∥V ∥+∥q∥=R0.

证明由引理4 以及文献[16]的引理12.1 可证得.

Pδ(E0)={(u,U,v,V,q)∈W :∥u∥+∥U∥+∥v∥+∥V ∥+∥q∥≤δ}.

证明对任意给定的充分小的ϵ0，取0<δ <δ0≪1，使得

记

因此，当(u,U,v,V,q) ∈Hδ+时，有∥u∥≤δz, ∥U∥≤δz, ∥v∥≤δz, ∥V ∥≤δz, ∥q∥≤δz.令ξ =2+γ −γx2，则ξ >0, ∀x ∈[0,1]，且满足ξxx<0, ξx(0)=ξx(1)+γξ(1)=0.易知(ξ,Qmin,1ξ,ξ,Qmin,2ξ,ξ)∈W.下面证明对任意的λ ≥0，方程

(u,U,v,V,q)−F(u,U,v,V,q)=λ(ξ,Qmin,1ξ,ξ,Qmin,2ξ,ξ)

为了证明系统正解的存在性，引入如下两个非线性特征值问题

证明 (i)和(ii)的证明完全类似，这里仅给出(i)的证明.定义

则方程F(t)(u,U,v,V,q)=(u,U,v,V,q)满足

以及边界条件(16).若(u,U,v,V,q)是F(t)在∂O+(E1)上的不动点，则u > 0, U >0, v ≥0, V ≥0, q > 0.由最大值原理必有v > 0, V > 0，否则(u,U,v,V,q) = E1，与(u,U,v,V,q)∈∂O+(E1)矛盾，即u>0, U >0, v >0, V >0, q >0.

首先证明对任意的t ∈[0,1], F(t)在∂O+(E1)上无不动点.假设(u,U,v,V,q) ∈∂O+(E1)是F(t)的不动点，则u > 0, U > 0, v > 0, V > 0, q > 0.当t =0 时，F(0)(u,U,v,V,q)=(u,U,v,V,q)满足