高中数学错题简单分类及应对策略
2020-09-05广东省东莞市第六高级中学523420
广东省东莞市第六高级中学(523420) 马 锋
1 数学错题的常见类型
1.1 知识性错题
知识性的错题是高中数学学习中最常见的一类错误.简单的来说,学生对知识点的模糊概念或者理解不够透彻,导致学生在练习中犯错.
1.1.1 基本概念理解不透
案例1设函数f(x)=xex,则( )
A.x=1 为f(x)的极大值点
B.x=−1 为f(x)的极小值点
错误解答f′(x)=(x+1)ex,令f′(x)=0 有x=−1,令f′(x)>0,有x >−1,令f′(x)<0,有x <−1,设函数f(x)在(−∞,−1)单调递减,在(−1,+∞)单调递增,且f′(−1)=0,此时,故为f(x)的极小值点,选D.
案例2函数f(x)=x2−1,则函数f(x)的零点是____.
错误解答(−1,0)和(1,0).
1.1.2 概念混淆
案例3从某企业生产的某种产品中抽取100件,测量这些产品的质量指标值,由测量结果得到如图所示的频率分布直方图,质量指标值落在区间[55,65),[65,75),[75,85]内的频率之比为4:2:1.
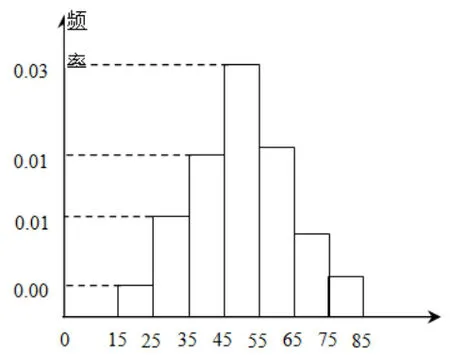
(1)求这些产品质量指标值落在区间[75,85]内的频率;
(2)若将频率视为概率,从该企业生产的这种产品中随机抽取3 件,记这3 件产品中质量指标值位于区间[45,75)内的产品件数为X,求X的分布列与数学期望.
错误解答(2)X的可能取值为0,1,2,3 则P(X=k)=.
分析特别是教毕业班的老师都知道,学生在超几何分布和二项分布上总是区分不清楚.人教版教材选修2-3P48 对超几何分布有详细的定义:一般地,在含有M件次品的N件产品中,任取n件,其中恰有X件次品,则,k=0,1,2,··· ,n,其中m=min{M,n},且nN,MN,n,M,,如果随机变量X的分布列满足上述形式,则称随机变量X服从超几何分布,而且课本是以正次品的抽取作为实际的例子.所以学生经常一看到正次品的质量问题马上想到超几何分布,其实这是一个误区.笔者认为,我们想搞清楚二者之间的区别,首先要搞懂“n次独立重复实验”这个概念,或者说这种模型.在“n次独立重复实验”的基础上,课本定义了二项分布:一般地,在n次独立重复实验中,用X表示时间A发生的次数,设每次实验发生的概率为p,则此时称随机变量X服从二项分布.
案例3 的第(2)问,题目告知:若将频率视为概率,从该企业生产的这种产品中随机抽取3 件,我们就应该抽象出3 次独立重复试验,所以X服从二项分布B(3,0.6),且数学期望EX=np=3×0.6=1.8.
1.2 逻辑性错题
1.2.1 推断能力出错
案例4已知条件p:x >0,条件则q是¬p成立的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既非充分也非必要条件
错误解答则即x >0,故选择C.
案例5直线x−y−k=0 与圆(x−1)2+y2=2 有两个不同交点”的一个充分不必要条件可以是( )
A.−1 C.0 错误解答直线x−y−k=0 与圆(x−1)2+y2=2有两个不同交点等价于即−1< k <3,(−1,3)⊆[−1,3]选B. 高中数学强调训练学生的推理能力,所以首先我们要注意推理的形式,推理的方向,理顺思路,找到推理的出发点至关重要. 1.2.2 分类讨论没有完备性 案例6a=1 是函数f(x)=sin 2ax最小正周期为π的( ) A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既非充分也非必要条件 错误解答f(x)=sin 2ax最小正周期为π,所以故a=1,故选择C,此题没有意识到实数a的正负号,当a >0 才有当a <0 时有此时a=−1,故案例6 的正确答案是A. 案例7已知函数求函数f(x)的单调区间. 错误解答因为令f′(x)=0,得所以函数f(x)的单调增区间为(0,x1)和(x2,+∞),单调减区间为(x1,x2). 案例7 是导数问题中最常见的含参分类讨论的问题,从一开始求导就有漏洞,首先应该注意函数的定义域为(0,+∞),然后是对新函数φ(x)=2ax2+x+1 零点的讨论. 案例8正项数列{an}的前n项和记为Sn,且满足.求数列{an}的通项公式. 错误思路当n=1 时,,解得a1=1,当n2 时,作差可得2an=,所以陷入繁琐的计算,而且很难化简. 案例9已知求4x+2y的取值范围. 错误思路①+②得即①-②得得所以. 教材对于我们教师提高课堂效率骑着很关键的指引作用.现在全国卷的实施,数学试题的难度增加,很多教师和学生开始练习更多难度的习题,而忽视了课本的重要性,个人觉得这是走进了一个误区.课本才是基础. 例如案例1 和案例2 就是学生对课本上极值点和函数零点概念没有理解清楚.人教版数学选修2-2 教材P27 对极值点和极值有明确的定义,如案例1 中,x=−1 为fx的极小值点,而则为函数f(x)的极小值,故正确答案应该选择B.案例1 中,人教版数学必修1 教材P87 对函数的零点有明确的定义:对于函数y=f(x),我们把使得方程f(x)=0 的实数x叫做函数y=f(x)的零点.故正确答案应该是x=±1. 所以我们经常会说:“零点不是点”.通过这两个典型案例,让学生进一步透彻的理解数学的基本概念.还可以延伸到极值点与极值与点的概念的比较. 课本不仅可以使学生掌握基础知识,进而消化教材的真正内涵.更重要的是学生不再通过拼命做题达到熟练程度的学习方法,不再是死记硬背,而是在对课本基本概念理解的基础上,进而实现知识的内化,自主学习能力的提高. 我在授课时,经常会和学生一起分析解题的过程.个人更强调步骤的有理有据,我经常会问:“下一步这样写有道理吗?”特别是含参问题,什么时候需要分类讨论了,其实标准很简单,举个实例:开车的时候,路是直的,我们一直往前开就行,什么时候需要考虑左转还是右转还是掉头呢,当然是有十字路口的时候.数学解题过程中,当你无法严谨直接的写出下一个步骤时,也许就是需要分类讨论的时候. 思考1在用二次方程求根公式之前是否考虑点什么呢? 分析二次方程ax2+bx+c=0 有一个大的前提就是a≠0,此题是含参问题,并没有给出参数a的取值范围,所以需要分a=0 和a≠0 两大类讨论. 思考2当a≠0 时,直接画出函数φ(x)的草图写出单调区间吗? 分析当然不行,a≠0 本身又包含两种情况,a >0 或a<0,所以应该继续分类. 思考3当a >0 时,φ(x)=2ax2+x+1=0,能够直接用求根公式吗?判别式可以直接写吗?根号是否有意义呢? 分析实数范围内求根公式的前提就是方程有根,判别式要有意义,案例7 中的明显当时是没有意义的. 思考4判别式∆=1−8a,我们是先讨论∆>0 还是∆0 呢? 分析其实应该先讨论∆0 时,虽然此时导函数方程没有实数根,但是没有实数根恰好就是最好讨论的,此时原函数必然就是单调的,更易讨论. 思考5当a <0,令φ(x)=2ax2+x+ 1=0,得 分析函数求导之前我们要注意书写定义域,此题的定义域为(0,+∞),由韦达定理可知两根为一正一负,很明显x1< x2,故x1<0,不在定义域内.所以,通过上述几个思考,案例7 的问题迎刃而解. 当a0 时,函数f(x)的单调递增区间是(0,+∞);当a<0 时,函数f(x)的单调递增区间是单调递减区间是. 最后,我们还可以适当小结一下: 第一步:讨论二次项系数是否为零 第二步:在二次项系数不为零的情况下,考虑判别式∆的符号 第三步:在判别式大于零的情况下,求出导函数方程的根,注意函数的定义域,甚至有的还要比较两个根的大小. 回到案例8:正项数列{an}的前n项和记为Sn,且满足.求数列{an}的通项公式.高中数列中出现Sn的时候,我们习惯性的想到Sn−1,然后进行作差运算化简,但是案例8 却很难算. 角度一观察表达式,我们发现右边an的表达式较为复杂,继续作差会让计算变得复杂,所以可以考虑一开始利用n2,an=Sn−Sn−1换掉an进行运算. 解析当n=1 时,,解得a1=1,当n2 时, 角度二高中数学课本上着重介绍了等差与等比数列,为什么呢?最简单的原因莫过于这两个是最常见的数列,归根结底是因为它们有明显的规律.那么我们解题的过程中出现的数列题目,一般肯定也是有规律可循的.所以我们可以用“发现→归纳→猜想→证明”的数学思想. 解析通过计算猜想然后用数学归纳法证明. 德国艾宾浩斯(H.Ebbinghaus)研究发现,遗忘在学习之后立即开始,而且遗忘的进程并不是均匀的.最初遗忘速度很快,以后逐渐缓慢.他认为“保持和遗忘是时间的函数”,并根据他的实验结果绘成描述遗忘进程的曲线,即著名的艾宾浩斯记忆遗忘曲线.这条曲线告诉人们在学习中的遗忘是有规律的,遗忘的进程很快,并且先快后慢.观察曲线,你会发现,学得的知识在一天后,如不抓紧复习,就只剩下原来的25%.随着时间的推移,遗忘的速度减慢,遗忘的数量也就减少. 对于数学学习来说,纠错就是一段不断成长的过程,但是仍旧有学生不懂、不会;懂了、不对;对了、不全;改了,有错.然后依次恶性循环.为什么高三还要第一轮、第二轮、第三轮复习,其实就是和错误与遗忘做斗争.所以,引导学生做好错题本是很有必要的. 错题本不是“抄题本”,也不是“作业本”,而是一本宝典,基本格式可以是:题目→分析→解答→批注(错误分析)→总结→变式. 数学是一门基础学科,我们从小学开始就开始学习数学,以数系的扩充来说,日常生活中的数青蛙引入到小学数学,有了正整数,小伙伴出去采蘑菇,猴子分桃,有了四则运算法则,求方程3x−2=0 引入了分数,求方程x2−2=0 的根,引入了无理数;求方程x2+2=0 的根,引入了虚数.这也是数系一个扩充最容易让学生弄明白的理由. 求本溯源,追求最本质的东西也是我们学习数学最应该注意的细节.高中数学的知识点和易错点其实是有限的,那么怎么样做到一个个的去纠正呢,并且记忆起来.需要的不光光是勤奋,还要有方法,建构知识网络,让我们更加轻松的学习数学.1.3 方法性错题
2 引导学生做好错题反思
2.1 回归课本
2.2 学会严谨的推敲思考
2.3 学会多角度分析问题
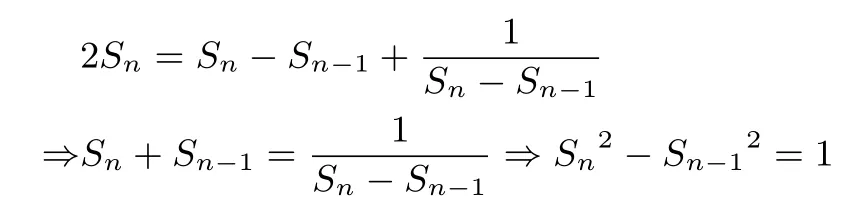
3 引导学生做错题本
