基于学生思维梯度的“中点四边形”教学设计*

广东省广州市五羊中学(510600) 陈思远

新人教版八年级下册[1-2]第十九章数学活动“中点四边形”这一节课是在学生经历了平行四边形和特殊平行四边形的学习后展开的.中点四边形的教学内容是本章设置的数学活动,是与四边形有关的一类有趣问题.通过本节课的学习,让学生巩固“四形一线”(平行四边形、矩形、菱形、正方形和三角形的中位线)的相关性质,同时落实本节课的三大教学目标:从知识技能上,理解原四边形的对角线对中点四边形的决定作用;从数学思想上,掌握利用中位线性质构造三角形的方法,实现把四边形问题转化为三角形问题进行解决;从数学研究方法上,让学生体会解决问题的一般过程:实验操作——猜想——证明——应用.

1 基于学生的思维梯度对教学设计的调整

1.1 打破“从特殊到一般”的惯性思维

《教师教学用书》[1]对这一教学内容,建议先从特殊的平行四边形入手,让学生观察任意四边形、平行四边形、矩形、菱形和正方形的中点四边形的形状,猜想并证明结论.然后通过信息技术工具,展现原四边形的动态变化过程,得出一般结论.这种教法符合我们研究问题的一般方法,从特殊到一般.但是,学生在证明特殊四边形的情况时,由于证明方法的多样性,学生较难感知原四边形的对角线对中点四边形的决定作用,因而对“一般”情况的猜想和证明造成障碍.基于对本课教学目标的考虑,体会决定中点四边形的本质所在,领悟数学中的转化思想,故决定调整本节课的教学安排,打破“从特殊到一般”的惯性思维,先为学生铺设阶梯,层层推进.

1.2 不满足于“平稳过渡”和“并列式”的迁移

最初的设计,是从任意的四边形出发,研究它的中点四边形的形状.通过添加条件,进一步研究“对角线互相垂直的四边形”的中点四边形的形状,让学生体会原四边形对角线作用的同时,明确研究问题的一般方法:实验操作(画图)——猜想——证明.在此基础上,提出问题:“对角线相等的四边形,它的中点四边形是什么形状?”此时,再引导学生仿照上一环节的活动过程,自主进行探究,从而降低“探究”活动的不确定性,避免让学生感到无处入手,不知所措.最后,再让学生归纳结论,应用新知.这一设计在一个教学班试教后,发现存在以下不足:(1)由于学生动手作图的能力有限,过多的时间和精力花费在画“对角线相等的四边形”上,导致后面的活动比较匆忙,无法突出本节课的教学目标,不能很好地让学生感知原四边形对角线的作用和转化思想;(2)由“对角线垂直”到“对角线相等”的研究方法是平行的过渡,学生大多是进行模仿操作,对学生的思维无法进行提升,思维缺乏跳跃导致整节课过于平淡和沉闷.

1.3 “条件探索”实现“让学生思维跳起来”

基于以上的问题,我们对教学设计进行了第一次调整和修改.学生在这一阶段的学习中,对“四种图形”的性质和判断方法比较熟悉,对“中位线”的性质也有一定的应用意识.而且在本节课的前两个环节:任意四边形和“对角线垂直的四边形”的中点四边形的研究中,对原四边形的对角线的作用已有一定的感知.所以环节三给出一个条件探索问题:如果中点四边形是菱形,则原四边形需要满足什么条件?此时,让学生在已有基础上,对问题进行分析,要证明是菱形,需要“一组邻边相等”,从而引导学生得出原四边形要满足“对角线相等”的结论.这一设计让学生从条件猜想证明结论,到从结论出发,反推条件,实现思维上的提升和跳跃.但是在试教后,仍然发现存在问题:(1)因为学生习惯于已有的思维模式,给定条件,思考结论,而这一条件探索问题,恰恰是相反的,对学生的思维是一次冲击和挑战,学生较难突破;(2)学生尝试通过画图解决,但是因为已知的是中点四边形的形状,学生较难画出原四边形,更不用说探究原四边形的性质了.

1.4 用“特殊”搭桥,实现自然跳跃

第二次的修改主要是针对环节二和环节三之间的过渡进行的.因为发现学生对条件探索问题的困难,所以在环节二后增加了一个“应用”,也是为后面的环节三做好思维上跳跃的准备.环节二学生已经知道“对角线互相垂直的四边形,它的中点四边形是矩形”.接着,教师再问“菱形的中点四边形是什么”,引导学生进行分析,因为菱形的对角线互相垂直,所以它的中点四边形是矩形.反过来,“矩形的中点四边形是什么?”学生通过自主画图,发现“矩形的中点四边形是菱形”,接着给出证明过程.这时,学生的证明方法是多样的,但是由前面两个环节的准备,学生能通过连结矩形的对角线进行证明,为后面的环节三做准备.此时,教师再自然过渡到“要使中点四边形是菱形,原四边形一定是矩形吗?还有其他的四边形,它的中点四边形是菱形吗?”学生在研究矩形的中点四边形时,已经知道对角线相等是决定中点四边形是菱形的关键.所以这一“特殊”的例子为“一般”问题的解决提供了一定的思考方向,为学生思维的跳跃提升铺设了阶梯.

2 教学过程设计

根据以上的分析,围绕本节课的教学目标,我们对各个环节的教学活动进行了如下调整.

初稿第一次修改稿第二次修改稿[活动1]以题点知:通过五道简单的练习题复习各类特殊四边形的性质和判定方法.[活动1]问题1:复习回顾各类特殊平行四边形的定义和关系.问题2:复习中位线的概念和中位线定理.[活动1]“四形一线”引出“中点四边形”问题1:复习回顾各类特殊平行四边形的定义和关系.(用韦恩图展示)问题2:复习中位线的概念和中位线定理.修改意图:快速激活与本课相关的知识点,“四形一线”既高度概括了前一阶段学习的主要内容,也引出了本节课的专题“中点四边形”.[活动2]定义:顺次连接任意四边形各边的中点,所构成的四边形以下简称为“中点四边形”.问题:如图,已知四边形ABCD,E、F、G、H分别是边AB、BC、CD、DA的中点.试判断中点四边形EFGH的形状,并说明理由.images/BZ_28_1734_2225_1999_2432.png设计意图:(1)从数学思想上,让学生理解如何通过正确添加辅助线构造三角形,以利用中位线性质解决问题.把四边形问题转化为三角形问题,是解决四边形问题的基本策略,体现了数学上的化归思想和转化思想.(2)通过证明思路的确立,让学生初步了解中点四边形是与原四边形的对角线密切相关的,并理解任意四边形的中点四边形是平行四边形.这一知识是研究后续内容的基础.[活动3]问题:如图（1）,已知四边形ABCD的对角线AC与BD互相垂直,E、F、G、H分别是边AB、BC、CD、DA的中点.试判断中点四边形EFGH的形状.images/BZ_28_1165_2735_1361_2955.pngimages/BZ_28_1428_2734_1627_2955.png图（1） 图（2）[活动3]问题:如图（2）,已知四边形ABCD的对角线AC与BD互相垂直,E、F、G、H分别是边AB、BC、CD、DA的中点.试判断中点四边形EFGH 的形状.

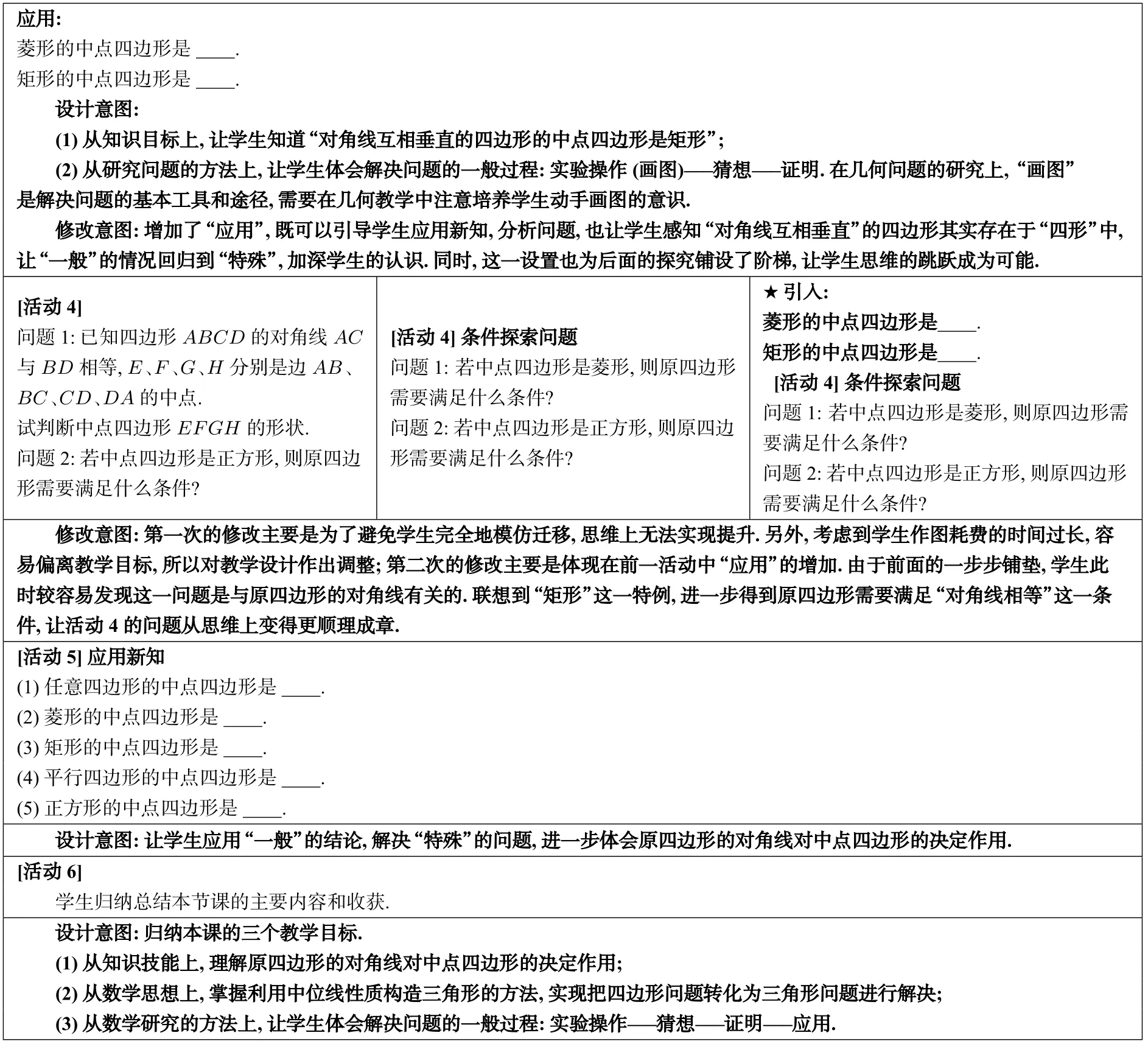
应用:菱形的中点四边形是.矩形的中点四边形是.设计意图:(1)从知识目标上,让学生知道“对角线互相垂直的四边形的中点四边形是矩形”;(2)从研究问题的方法上,让学生体会解决问题的一般过程:实验操作(画图)——猜想——证明.在几何问题的研究上,“画图”是解决问题的基本工具和途径,需要在几何教学中注意培养学生动手画图的意识.修改意图:增加了“应用”,既可以引导学生应用新知,分析问题,也让学生感知“对角线互相垂直”的四边形其实存在于“四形”中,让“一般”的情况回归到“特殊”,加深学生的认识.同时,这一设置也为后面的探究铺设了阶梯,让学生思维的跳跃成为可能.[活动4]问题1:已知四边形ABCD的对角线AC与BD相等,E、F、G、H分别是边AB、BC、CD、DA的中点.试判断中点四边形EFGH的形状.问题2:若中点四边形是正方形,则原四边形需要满足什么条件?[活动4]条件探索问题问题1:若中点四边形是菱形,则原四边形需要满足什么条件?问题2:若中点四边形是正方形,则原四边形需要满足什么条件?#引入:菱形的中点四边形是.矩形的中点四边形是.[活动4]条件探索问题问题1:若中点四边形是菱形,则原四边形需要满足什么条件?问题2:若中点四边形是正方形,则原四边形需要满足什么条件?修改意图:第一次的修改主要是为了避免学生完全地模仿迁移,思维上无法实现提升.另外,考虑到学生作图images/BZ_29_1870_1181_1902_1213.png费的时间过长,容易偏离教学目标,所以对教学设计作出调整;第二次的修改主要是体现在前一活动中“应用”的增加.由于前面的一步步铺垫,学生此时较容易发现这一问题是与原四边形的对角线有关的.联想到“矩形”这一特例,进一步得到原四边形需要满足“对角线相等”这一条件,让活动4 的问题从思维上变得更顺理成章.[活动5]应用新知(1)任意四边形的中点四边形是.(2)菱形的中点四边形是.(3)矩形的中点四边形是.(4)平行四边形的中点四边形是.(5)正方形的中点四边形是.设计意图:让学生应用“一般”的结论,解决“特殊”的问题,进一步体会原四边形的对角线对中点四边形的决定作用.[活动6]学生归纳总结本节课的主要内容和收获.设计意图:归纳本课的三个教学目标.(1)从知识技能上,理解原四边形的对角线对中点四边形的决定作用;(2)从数学思想上,掌握利用中位线性质构造三角形的方法,实现把四边形问题转化为三角形问题进行解决;(3)从数学研究的方法上,让学生体会解决问题的一般过程:实验操作——猜想——证明——应用.

3 教学后记

本节课始终从学生的思维特征出发,对教学设计进行修改和调整,以求使预设和生成达到和谐统一.深入研究学生的活动和思维特征,为预设和生成搭建了有效的桥梁.

3.1 以生成为导向,提高预设的针对性

充分考虑学生已有的知识结构和思维特征,进行本课的教学设计.几何探究课对学生来说具有较大的难度,具有一定的开放性,所以必须更充分地“备学生”.通过分析学生可能出现的各种情况和试教情况,对教学设计进行修改和调整,让预设更有针对性,特别是对于本课三大教学目标的落实发挥了更好的导向作用.

3.2 充分预设,提高生成的质量

在充分挖掘教材内容后,根据学生已有的知识结构,对本课的教学目标、教学内容、教学过程、教学方法进行了设计.为了让学生的思维避免平移式的过渡,对教学环节进行了第一次修改,重新设置了条件探索问题,让学生的思维得到训练和提升.另一方面,为了让学生的探索更具有方向性,增加了“特殊”例子进行启发,让课堂上的生成与预设达到和谐统一.

本节课给了我很多的启发.预设是前提,生成是关键,将预设和生成结合起来不仅是一门教育的科学,更是一门教育的艺术.作为一名经验尚浅的青年教师,我在以后的教学工作中,将继续以学生的思维特征搭建预设和生成的有效桥梁,让预设和生成更好地服务于学生的成长.