动态猫变换和混沌映射的图像加密算法

韩雪娟，李国东

(新疆财经大学 应用数学学院，新疆 乌鲁木齐 830012)

0 引 言

由于混沌所具有的特性，对于混沌和超混沌在图像加密技术中的应用越来越受到学者的关注，已经成为了研究热点之一[1-6]。数字图像加密主要是根据美国数学家香农提出的置乱技术和扩散技术，利用置乱方法和扩散方法对图像信息进行隐藏。

Arnold变换的特点如下：算法简单、置乱效果好，因此被广泛应用到图像加密方面[7,8]。但是Arnold变换具有周期性的特点限制了它在图像加密方面的应用，怎样避开它的弊端设计出更好的加密算法成为研究的热点之一。有些学者在图像加密方面的文献中提出了改进Arnold变换的加密方法[9,10]。也有许多学者设计了各种不同类型的加密算法，姚丽莎等[11]利用DNA序列和分数阶Chen超混沌系统对彩色图像进行加密，DAN加密具有难破解的优点。谢国波等[12]利用引入量子混沌的方法，设计了一种使用量子混沌实现比特置乱的图像加密方案，使算法不会受混沌参数少的缺陷的影响。仿真结果表明，该算法在统计特性分析、抗攻击性能上要比常规算法更胜一筹，但是不足之处在于比特置乱这个算法本身计算量较大，导致效率不高。毛颉等[13]根据引擎值来动态选择加密密钥，设计了4方向连续扩散的方法，设计了一种算法完成图像加密。Yueping Li等[14]采用5维多翼超混沌系统，超混沌系统生成的密钥流与原始图像相关。Rasul Enayatifara等[15]提出了一种同步置换扩散技术，该方法快速有效。

本文设计的加密算法在置乱时融合了分块置乱和动态Arnold变换，有效避开了Arnold置乱具有周期性易破解的弊端。同时在扩散算法中利用3种不同的混沌映射产生伪随机序列，对置乱后的加密图像进行分块扩散和整体扩散；在分块扩散时根据Logistic映射选取的子块奇偶性选择不同的随机序列分别进行加密，混沌之间相互控制参数，大大增加了密文的安全性。

1 加密算法的设计

1.1 加密原理

本文设计的加密方案不但增大了解密难度，而且提高了加密信息的安全级别。该算法对明文图像分别进行了两种不同方式的置乱，第一种是分块置乱，第二种是Arnold置乱。再运用第二种方式置乱时又对一次置乱后的图像进行了3次动态置乱，避免了Arnold置乱的周期性带来的影响，破坏了明文图像之间的联系，增加了图像的置乱程度。得到最终的置乱图像后，对图像进行了两次扩散，每次扩散选择不同的混沌序列，增强了密文图像的安全性；同时混沌序列之间又相互控制参数，增加了密文的破解难度。

图像置乱操作：先对图像进行第一次置乱，再利用动态Arnold映射对分块置乱后的图像进行置乱；图像的扩散部分：迭代处理Tent-Sine映射、Tent映射以及Sine映射产生3个不同的序列X、Y、Z，迭代处理Logistic映射产生的序列w″选块。先是用序列X或者Y对置乱后的图像依次进行第一次分块扩散，再用序列Z对一次扩散后的加密图像进行第二次整体扩散，得到最终加密图像。经过模拟仿真，该方法解决了安全级别不高和易破解的问题。

1.2 置乱算法的设计

(1)分块置乱：

设明文图像大小为m*n的灰度图像E, 将其划分为大小为t*t的矩阵子块，共有m/t*n/t个子块(t是m,n的公约数)，本文选用的是300*300的灰度图像。

将E平均分为25块60*60的图像，记为e1,e2,e3,…,e25， 表示如下

e1=(e11,e12,e13…e1t*t)
e2=(e21,e22,e23…e2t*t)
e3=(e31,e32,e33…e3t*t)
⋮
e25=(e251,e252,e253…e25t*t)

(1)

这25个矩阵子块进行如下方式的分块置乱

ei01=ei(i∶25∶t*t)
ei02=ei(i∶25∶t*t)
ei03=ei(i∶25∶t*t)
⋮
ei25=ei(i∶25∶t*t)

(2)

置乱后的矩阵子块记为

Ei=(ei01,ei02,ei03…ei25)

(3)

其中， i=1,2,3…25， 将25个置乱后的矩阵子块重新组合成为一个300*300的大矩阵E′。

(2)动态Arnold变换：

Arnold映射的方程为

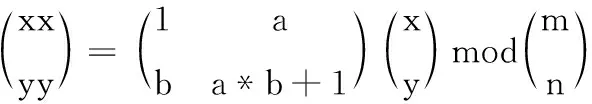
(4)

控制参数a,b， (x,y) 为明文图像的像素位置坐标， (xx,yy) 为置乱后图像的像素位置坐标。Arnold映射将原图像中的点 (x,y) 处的像素值存储到变换后的点 (xx,yy) 处，经过变换后明文图像会变得模糊，经过多次变换后即可得到最终的加密图像，加密图像呈现为一幅杂乱无章的图像，完全看不出明文图像的信息。

为了消除Arnold变换周期性对于加密图像的影响，本文采用一种动态Arnold置乱方式分别进行3次Arnold变换。将矩阵E′均匀分成25块，每块大小为60×60，如图1所示。

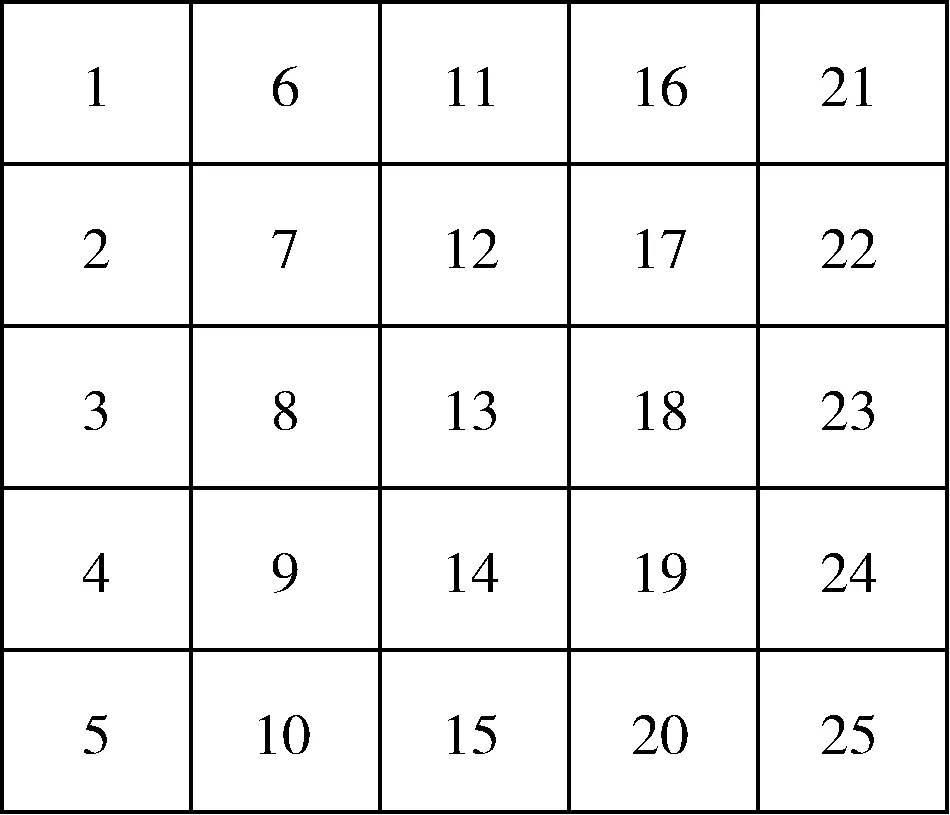
图1 E′分块

Arnold第一次置乱：从矩阵E′中选择矩阵子块1,2,3,6,7,8,11,12,13组成一个3*3的矩阵A， 对其进行 Arnold 变换。参数： a1=21, b1=1， 迭代次数： n/gcd(m/t,n/t) (gcd(m/t,n/t) 表示m/t,n/t的最大公约数)，通过第一次Arnold变换后得到一个新的3*3的矩阵A′，如图2所示。

图2 A′分块

Arnold第二次置乱：在矩阵A′中选择矩阵子块7,8,12,13分别替换E′矩阵中的矩阵子块7,8,12,13得到新的矩阵EE。 在矩阵EE中选择矩阵子块7,8,9,10,12,13,14,15,17,18,19,20,22,23,24,25组成一个4*4的矩阵B， 对其进行Arnold置乱，参数： a2=1,b2=1， 迭代次数： n/gcd(t,t)， 通过第二次Arnold变换后得到一个新的4*4的矩阵B′， 如图3所示。

图3 B′分块

Arnold第三次置乱：用第二次Arnold置乱后的矩阵块B′替换矩阵E′中的相应位置得到矩阵大小为60*60的新矩阵EE′， 对其进行Arnold置乱，参数： a3=1, b3=21， 迭代次数： n/gcd(m/t,n/t)， 通过第三次Arnold变换得到一个新的5*5的矩阵EE″， 该矩阵即为置乱后的密文矩阵。

1.3 扩散算法的设计

1.3.1 混沌序列的分析

本文中用到的混沌映射分别为：Tent-Sine映射、Tent映射、Sine映射以及Logistic映射，它们的动力学方程如下所示。

Tent-Sine映射[10]

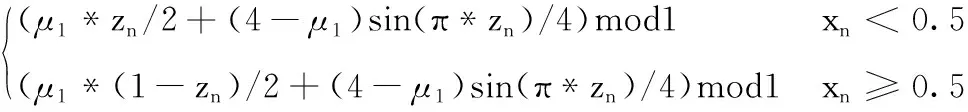
(5)

Tent映射

(6)

Sine映射

yn+1=μ3*sin(π*yn)/4mod1

(7)

Logistic映射

wn+1=μ4wn(1-wn) w∈[0,1],μ4∈(0,4]

(8)

其中，取模是为了保证输出的数据在区间(0,1)之间，n为迭代次数，μ1,μ2,μ3,μ4为系统控制参数， x0,y0,z0,w0为初始值，当μ1∈(0,4),μ2∈(0,2),μ3∈[3.48,4] 时，映射呈现出混沌行为。

1.3.2 混沌序列的生成

给定密钥

k1=345
z0=0.3789,μ1=1.1221
x0=z(1),μ2=2^(s/(m*n*255))
y0=x(1),μ3=3.496
w0=y(1),μ4=4

(9)

以上公式中s表示的是明文图像中所有的像素值之和。

(1)将Tent-Sine映射迭代m*n次，产生如下序列

z={zj|j=1,2，…，m*n}

(10)

从k1+1项开始选取，通过下式对序列进行处理

z1=mod(floor(z*10^5-floor(z*10^5)*10^2),4)

(11)

得到序列

z1={zi|i=1,2，…，q}

(12)

再按照下式对序列进行处理

Z=mod(floor(z*10^6-floor(z*10^6)*10^3),256)

(13)

得到序列

Z={Zj|j=1,2，…，m*n}

(14)

式中： q=t2, k=k1+q。

(2)分别迭代k次式(6)、式(7)，选择序列z1中的前q-1项作为采样间隔，对迭代产生的混沌序列x,y从第k1-1项开始抽样，再截取它们的前q项按照下式进行处理

X=mod(floor(x*10^6-floor(x*10^6)*10^3),256)

(15)

Y=mod(floor(y*10^6-floor(y*10^6)*10^3),256)

(16)

得到序列

X={Xi|i=1,2，…，q}

(17)

Y={Yi|i=1,2，…，q}

(18)

其中，序列X,Y用于像素的一次扩散，序列Z用于像素的二次扩散。

(3)迭代式(8)3*k1次，按照下式对序列进行处理

w=ceil(mod(w*10^13,25))

(19)

w′=w(851∶950)

(20)

在w′中从第一项开始无重复的选取[1,25]中的数字，直到选满25个数字停止，得到序列

w″={w″1,w″2，…，w″25}

(21)

为了判断序列w″的奇偶性，对序列做如下处理

w1=mod(w″,2)

(22)

得到全为0、1的25个数组成的序列w1。

1.3.3 扩散算法的描述

一次扩散过程：将置乱后密文EE″均匀分成25块大小为60*60的图像，记为EE″1,EE″2,EE″3,…,EE″25， 表示如下

EE″1=(EE″11,EE″12,EE″13…EE″1t*t)
EE″2=(EE″21,EE″22,EE″23…EE″2t*t)
EE″3=(EE″31,EE″32,EE″33…EE″3t*t)
⋮
EE″25=(EE″251,EE″252,EE″253…EE″25t*t)

(23)

当w″i中的数字是奇数时

ci=e1⊕((X+EE″w ″i)mod256⊕X)

(24)

当w″i中的数字是偶数时

ci=e25⊕((Y+EE″w ″i)mod256⊕Y)

(25)

其中，e1，e25为明文图像中的两个子块， i=1,2,3…25。 将经过上式处理后的ci合成m*n的大矩阵得到矩阵C， 对它进行二次扩散

D=C⊕Z

(26)

得到最终加密图像D。

2 算法的流程与步骤

本文加密算法的流程如图4所示。

本文加密算法的具体步骤如下：

(1)首先选择一幅合适的数字图像作为明文图像，得到明文图像的数字矩阵E，明文图像的大小为300*300；

(2)将E划分为大小为60*60的矩阵子块，得到5*5个子块e1,e2,e3,…,e25；

(3)对e1,e2,e3,…,e25进行分块置乱，将25个置乱后的矩阵子块重新组合成为一个300*300的大矩阵E′；

(4)对分块置乱后的密文进行动态Arnold置乱，①将矩阵E′均匀分成25块，选取一个大小为3*3的矩阵子块A进行Arnold置乱,得到变换后的A′矩阵,再用其替代矩阵E′中的A矩阵，得到一个新的大小为300*300的矩阵EE。②在矩阵EE中选择一个大小为4×4的矩阵子块B进行Arnold置乱，得到变换后的B′矩阵，再用它替换矩阵EE中的B，得到一个大小为300*300的矩阵EE′。 ③对矩阵EE′进行Arnold置乱，得到最终置乱加密矩阵EE″；

(5)迭代、处理Tent-Sine映射、Tent映射、Sine映射以及Logistic映射，得到混沌序列Z、X、Y、w″；

(6)对最终置乱后加密矩阵EE″均匀分块，得到5*5个大小为60*60的矩阵子块EE″1,EE″2,EE″3,…,EE″25， 对这些矩阵子块进行第一次扩散加密，将一次扩散后加密矩阵合并成300*300的矩阵C；

(7)对分块扩散后的加密图像进行第二次整体图像的扩散加密过程，得到的扩散后的图像即为最终的加密图像D；

(8)密文图像的解密过程也就是图像加密过程的逆过程。用下式替代式(24)和式(25)

EE″w ″i=mod(ci⊕e1⊕X+256-X,256)

(27)

EE″w ″i=mod(ci⊕e25⊕Y+256-Y,256)

(28)

图4 加密算法流程

3 仿真实验

Lena图像实验仿真效果如图5所示。利用本文设计的加密算法对图5(a)进行加密，分块置乱后得到第一次置乱密文图5(b)，从图中可以看出图像呈现出纵向的明暗分块；再对一次置乱后的图像进行动态Arnold置乱，得到最终的置乱加密图5(c)。对图5(c)进行两次扩散得到最终加密图5(d)。从图5可以看出：经过加密过程后，从最终的密文图像中已看不出明文图像的轮廓，最终的加密图像变成一副密密麻麻的黑白点相杂的图像，可见达到了加密的目的。

图5 加密效果

4 算法统计特性分析

4.1 直方图分析

直方图分析结果如图6所示。根据直方图理论可知：当每个灰度级出现的次数越接近，即直方图越平稳时，也就说明密文图像的安全性就越高。由图6可知，明文和密文图像直方图相差很大，图6(a)能量分布不均匀，加密后的直方图6(b)比较平滑、像素的能量分布是均匀的，说明密文图像较稳定。

图6 明密文图像直方图分析

4.2 算法密钥的空间和敏感性分析

本文设计的加密算法中，通过利用4种不同的混沌系统相互控制参数，在很大程度上增加了解密的难度；同时多种混沌映射的初值和参数一同作为密钥，使得密钥空间至少达到10240，因此算法能够有效抵抗穷举攻击。

在密钥敏感性的分析中，为了确定密钥是否具有敏感性将Tent映射的密钥Key减少1013，解密后无法得到正确的明文图像，如图7所示。可以知道本文设计的算法具有很强的敏感性，即使使用与正确密钥相差很小的密钥进行解密，得到的仍是与原图不一样的错误解密图。

图7 不正确的解密图像

4.3 抗差分攻击能力分析

根据NPCR(像素改变率)、UACI(归一化平均改变强度)的定义，如文献[16]所描述的。D1表示密文，D2为明文图像像素值发生改变时的密文，公式如下所示

(29)

(30)

任意取明文图像中的坐标(1,159)，将它改为(11,159)，得到NPCR和UACI值见表1。

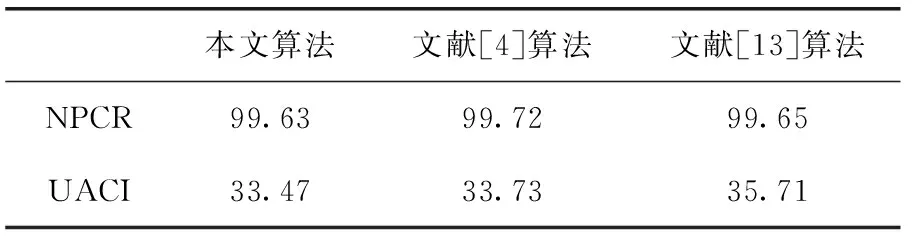
表1 NPCR与UACI/%

从表1可以得出如下结论：本文设计的加密算法得到的NPCR和UACI值分别为99.63%和33.47%，其值更加接近于NPCR和UACI的理想值99.6094%和33.4635%；并且在与文献[4]和文献[13]进行对比后，发现本文具有更强的抗差分攻击能力。

4.4 算法信息熵分析

因为信息熵是图像信息不确定性的体现，所以如果信息熵较大，那么可视信息就会比较少；反之如果信息熵较小，那么可视信息就会较多；信息熵的理想值为8。计算公式如下所示

(31)

本文的加密算法计算的信息熵是7.9980，而文献[4]和文献[13]得到的信息熵分别为7.9967和7.9417，本文的信息熵明显高于文献中的信息熵，而且更加接近于理想值8，因此该算法能够很好抗统计攻击性。

4.5 相关性分析

根据相关系数r的定义，在明密文图像中任意选择N对像素值，分别计算明密文图像水平、垂直和对角方向上的相关系数r，验证明文图像和密文图像相邻像素之间的相关性，相关系数计算公式如下

(32)

(33)

(34)

(35)

如果 (xi,yi) 是ui的坐标，那么当 (xi+1,yi)、 (xi,yi+1)、 (xi+1,yi+1)、 (xi-1,yi+1) 均是vi的坐标时，最终得到的相关系数值就分别是水平方向上的相关系数、垂直方向上的相关系数、正对角上的相关系数以及反对角上的相关系数。明文图像与密文图像的相关性散点如图8所示，相关系数见表2。

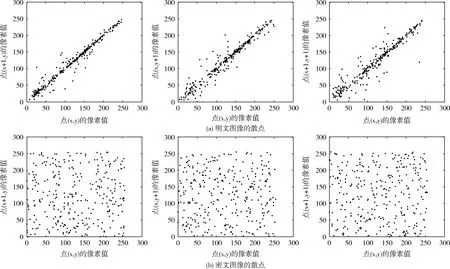
图8 明文图像与密文图像的相关性

表2 相关系数值

由图8可以得出如下结论：明文图像的散点图无论在水平方向、垂直方向，还是对角方向上都基本呈一条直线，具有明显的线性关系；而密文图像的散点图杂乱无章，呈现出散乱的点，在各个方向上没有变现出存在任何关系。从表2看出：明文图像的相关系数都超过0.95和1很相近，说明具有很强的相关性；而密文图像的相关系数都小于0.005接近于零，可以说不存在相关性。从与文献比较的结果可以发现本文计算的相关系数均小于文献中的相关系数，说明本文设计的加密算法打乱了原始图像中相邻像素点之间的相关性，加密的效果比较好。

5 结束语

本文设计的加密算法是通过软件Matlab 2017进行实验的，在Windows 8操作系统中进行。本文设计的算法对图像进行了两次置乱操作以及两次扩散操作，置乱算法：第一次是分块置乱，对5*5个子块进行置乱；第二次是在第一次分块置乱的基础上进行动态Aronld变换(对第一次置乱后的图像进行三次Arnold置乱)，最终得到置乱后的加密图像。扩散算法：迭代处理Tent-Sine映射、Tent映射、Sine映射以及Logistic映射分别产生混沌序列Z、X、Y、w″，对最终置乱后的密文图像进行扩散操作。序列Z用于第二次整体扩散，序列X、Y用于第一次分块扩散，经过两次扩散后得到最终加密图像。

实验结果表明：本文设计的加密算法通过混沌系统之间相互控制参数增大了算法的密钥空间，解决了密文图像容易被破解，导致密文信息安全性不够高的问题；同时经过实验仿真发现密钥具有很强的敏感性；因此该算法具有较好的加密效果，可以应用于图像加密中。