具有最优负载均衡性的纠删码修复流水线
2020-09-04江小玉李贵洋胡金平韩鸿宇
江小玉,李贵洋,胡金平,韩鸿宇
(四川师范大学 计算机科学学院,四川 成都 610101)
0 引 言
大数据时代,分布式存储集群承载的数据量规模日益扩大,需要以更加经济有效的方式保障数据的可靠性[1]。纠删码(erasure code)[2,3]因具有高容错性和低冗余度的特点,在许多大规模分布式存储系统中已得到实际应用,比如 Google[5]、Facebook[6]、Hadoop[7]等互联网国际巨头。但是,纠删码的修复代价高昂[8],修复时从其它可用节点上下载数据并进行译码,会对计算和网络资源造成巨大的压力。由于互联网中的网络带宽资源有限,网络带宽成为了系统的性能瓶颈[9]。
数据在网络中的传输时间占总修复时间的94%[10],数据节点发生故障后如何实现快速恢复是目前纠删码研究领域的一个重点。一方面可以通过减少总的网络带宽从而减少对网络资源的占用[11],另一方面是消除系统中的网络性能瓶颈[12]。例如:纠删码修复流水线(RP)[13]通过改变网络传输结构,消除瓶颈节点,减少了90%的修复时间。但是,现有的纠删码修复流水线中存在修复工作部署不均,节点负载不够均衡的问题。
为了均衡节点的负载,提高纠删码的修复性能,本文提出了一种网络结构Optns。Optns中多构造了一条流水线路径。理论分析及实验结果表明,与RP原始网络结构相比,Optns不仅以O(1)的时间完成了故障修复,而且所有帮助(参与修复的)节点均摊了修复过程中的工作量,具有最优的负载均衡性。
1 相关理论基础
1.1 问题定义
首先,将本文的相关参数统一罗列成表,具体见表1。

表1 参数
其次,给出本文相关的性质和术语定义。
性质1 (最大距离可分离码):最大距离可分离(maximum distance separable,MDS)码通常用于通信和存储系统中的各种应用。一个(k,r)-MDS码取一个大小为B的文件,将其分成大小相等的k个块后编码,生成r个检验块,形成一个纠删码组(共包含n个编码块),分别存放在n个独立的节点上。读取其中任意k块,通过译码运算可修复一个故障数据块,编码后的系统最多可容忍任意r个原始数据块或校验块发生故障。可知
n=k+r
(1)
定义1 数据切片:将数据文件切分为固定、更小的单位,称为数据切片。
定义2 时间片段:将修复过程划分时间片段,每个时间片段内只有一个数据切片可以通过网络链路传输。
定义3 节点负载:系统修复一个故障时,节点所承担的工作量。
1.2 纠删码修复流水线原理
修复流水线基于最典型的纠删码算法——里德-所罗门码(Reed-Solomon,RS)。RS码是一类MDS编码,修复任何一个故障时的代价为k,即需要从其它磁盘上读取,并在网络上传输k份数据。互联网中节点的网络带宽比较低时会造成修复拥塞,网络资源成为了系统的性能瓶颈。
如图1(a)所示,纠删码常规修复中,帮助节点(用集合N={Ni|1≤i≤k}表示)串行将本地的数据发送给代替(代替故障节点的新)节点R,R收集齐数据后做译码运算。k个帮助节点竞争R的网络资源导致链路拥塞。并且,R节点需要做全部的运算,工作繁重,容易成为系统的瓶颈节点。因此,采用纠删码修复流水线分而治之,通过改变传输结构的方式重新分配网络流量,将译码运算分散到各个帮助节点,RP拓扑结构如图1(b)所示。假设a={a1,a2,…,ak}为译码系数,b={b1,b2,…,bk}为帮助节点上的数据。则修复流水线的工作流程为:N1发送数据a1b1,N2将本地的数据乘以相应的系数,与从N1接收的数据进行数据组合,然后将计算后的数据(a1b1⊕a2b2)转发给N3(“⊕”表示二元域上的加运算,即异或运算)。帮助节点间发送的数据量大小是相同的,因为异或运算不会改变数据块的大小。以此类推,直到将恢复后的数据发送给一个新的节点R。此时,系统中不存在瓶颈节点,可显著减少修复时间。
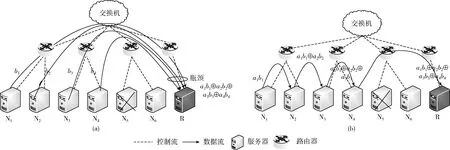
图1 常规修复vs修复流水线拓扑
从图1(b)的拓扑图抽象出RP的网络结构Cyclic[13],如图2(a)所示,Cyclic构造了多条不同的流水线路径,将数据文件切分为更小的单位后分组进行修复。Cyclic修复流程如下:
t1时刻,第一组流水线启动,N1、N2、N3同时开始发送数据。
t2、t3时刻,N1~N4作为中间节点,接收、计算并转发数据给下一个节点。
t4时刻,第一组流水线负责的数据修复完成。
t5时刻,第二组流水线启动,同时N4将第一组中修复完的第一个数据切片发送给R。
t6时刻,第二组的修复流水线继续工作,N1也将在第一组中修复好的第二个数据切片发送给R。

图2 网络结构(k=4,m=2,s=6)
在相同的模式下持续修复,直到整个修复工作完成。分布式存储系统中,R作为代替节点比一般的节点分布的更远,常位于网络边缘,因此与R的交互受限更多。帮助节点循环参与修复中的各项工作,例如N1在t1时刻发送数据;t3时刻接收、计算、转发数据;t6时刻将数据发送给R,参与了每一项修复任务。但是可以看出,Cyclic存在缺陷:N3节点没有与R交互,即没有承担工作量最大的修复任务,这一部分工作由部分帮助节点承担,导致负载不够均衡。
2 Optns网络结构
在Cyclic的基础上进行改进,设计了Optns网络结构,它能完全均衡帮助节点间的负载,使帮助节点间的负载相同。Optns仍保持纠删码修复流水线的基本原理,它的核心思想在于:为了让所有的帮助节点均摊负载,每个帮助节点都必须参与所有的修复任务。因此,在选定k个帮助节点后,通过空置时间片段的方法构造更多的流水线修复路径。Optns的构造步骤如下:
(1)当系统发生故障时,从剩余的可用节点中任意选取k个节点用于修复。
(2)将数据文件切分为s个大小相等的数据切片。
(3)构造不同的修复流水线路径。k个帮助节点依次排列,每次将帮助节点循环左移一位,k个帮助节点可以构造k条不同的路径。
(4)分组并行修复。每一条流水线上有(k-1)个时间片段,可供(k-1)个节点将数据传输给R,即每一组修复中可以并行调度(k-1)条不同的流水线。假设修复完一个故障所需的时间为t,则一个时间片段耗费的时间为t/s。
(5)空置时间片段。第一组流水线传输修复完数据后,Nk节点推迟第一个数据切片发送给R的启动时间,Nk在tk+1时刻作为第二组流水线的启动节点。此时,k条不同的线性路径都调度了,共有k个节点与R交互,负载最重的修复任务均匀分配给了所有帮助节点,其它的工作也随之均匀分配。
Optns结构如图2(b)所示,空白区块表示空置的时间片段。Optns的修复过程与Cyclic类似:
t1时刻,第一组的流水线启动。
t2、t3时刻,传输数据进行修复。
t4时刻,第一组负责的数据修复完成,但还没有把修复完成的数据传输给R。
t5时刻,第二组启动,N4开始工作,给N1传输数据。如果N4同时发送数据给R,节点将被重载,出口带宽资源被竞争,可能导致拥塞。因此,空置一个时间片段,推迟给R发送数据的时间。
t6时刻,N4将数据发送给R。以N4为启动节点的流水线的终端节点为N3,因此,所有的帮助节点都会参与每一项修复任务。
t6时刻及以后,帮助节点全部并行,系统中不再有空闲的帮助节点,修复效率达到最高。
对比图2(a)和图2(b),Optns结构与Cyclic结构最大的区别在于,Cyclic只构造了(k-1)条不同的流水线路径,剩余一个帮助节点没有参与和请求节点交互的修复任务,节点的负载不够均衡。而Optns构造了k条不同的流水线,所有帮助节点都会循环参与每一项子任务,十分均衡。
3 理论分析
为了评价Optns的性能,以节点负载L和修复时间T作为评判标准。
3.1 计算节点负载算法
由于与请求节点的交互工作量最大,节点负载不均衡的瓶颈集中在此,因此只分析帮助节点对这一部分工作量的摊分情况。经研究后,提出通用算法1,计算节点的负载,具体步骤如下。
算法1:计算节点负载
输入:B、C、α; //B表示发生故障的数据块大小,C表示单位数据量,α表示修复单位数据量,与R交互时的工作量。
输出:节点负载L。
过程:
(1)P=NULL; //P表示与R交互的帮助节点集合;
(2)FORi=1 tokin N
IFNi与R交互 and Ni不存在P中THEN
把Ni加入集合P
ENDIF
ENDFOR
(3)d=crad(P);//crad()表示集合元素的个数;
(5) 输出节点负载L,算法停止。
3.2 计算修复时间
纠删码系统的故障修复时间实际上由几部分组成,计算公式如下
Trepair=TI/O+Ttrans+Tcompute
(2)
其中,Trepair表示总的修复时间,TI/O表示磁盘I/O时间,Ttrans表示数据传输时间,Tcompute表示译码计算时间。数据在网络中的传输时间占比高达94%,为了避免其它因素的干扰,本算法中忽略磁盘的I/O时间和计算时间,令
TI/O=0,Tcompute=0
(3)
根据式(2)、式(3),修复时间Trepair=Ttrans。基于此,提出通用算法2,计算修复时间,具体步骤如下。
算法2:计算修复时间
输入:s、k、t; //s表示数据切片的个数,k表示帮助节点的个数,t表示修复一个数据块故障的时间。
输出:修复时间T。
过程:

(2)FORi=1 to (g-1)
tg=(k-1) // 每一条流水线消耗的时间片段数量。
ENDFOR
(3)ttrans=s;//将所有修复完的数据切片依次传输给R消耗的时间片段。
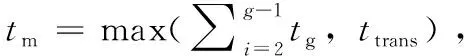
(5) 总的修复时间片ttotal=tg+tm=(k-1)+s;
(6) 修复一个数据块故障的时间为t,则一个时间片段消耗的时间为th=t/s;
(7) 输出总的修复时间T=ttotal×th,算法停止。
3.3 理论分析
3.3.1 节点负载
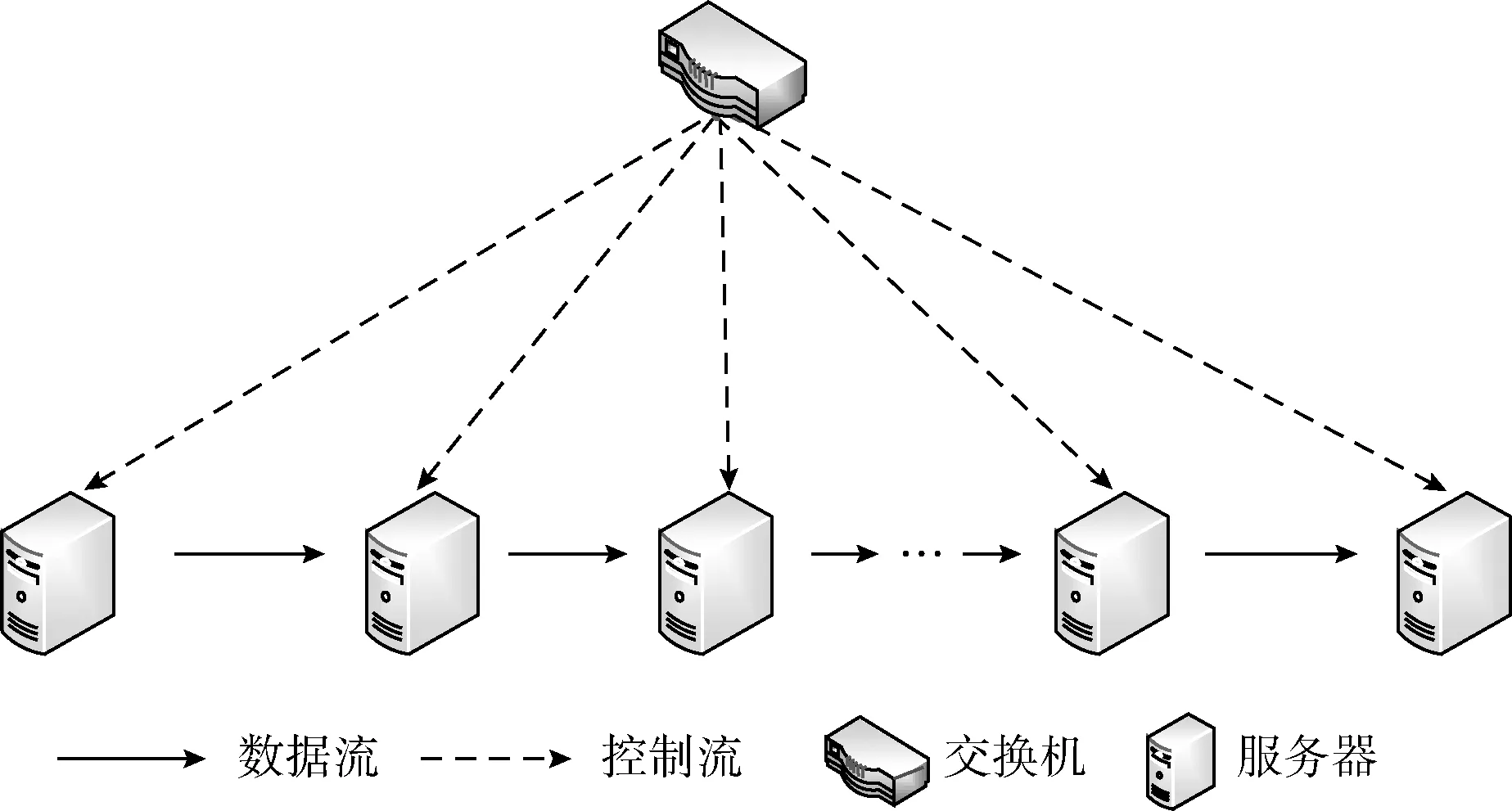
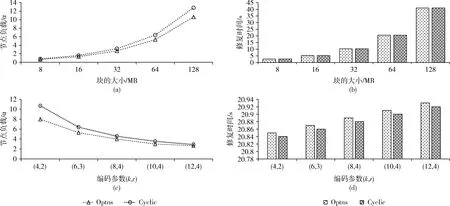
Cyclic有(k-1)条不同的流水线路径,即有(k-1)个帮助节点与R交互,根据算法1,节点的负载为LCyclic=αB/(k-1)C。同理,Optns有k个帮助节点与R交互,负载LOptns=αB/kC。显然LOptns ΔL=(LCyclic-LOptns)/LCyclic×100%=1/k (4) 因此,Optns减少了帮助节点对工作量最大的修复任务的分摊量,均衡了节点的负载。 3.3.2 修复时间 根据通用算法2,原始的网络结构Cyclic的修复时间TCyclic= (k-1 +s)×(t/s)=[1+(k-1)/s]t。Optns结构中空置了一个时间片段,需要加以计算,修复时间TOptns=(ttotal+1)th=(1+k/s)t。Cyclic与Optns的时间差 ΔT=TOptns-TCyclic=t/s (5) 相比Cyclic,Optns虽然增加了一个空闲的时间片段,但并不会对整体的修复时间造成任何消极影响,时间复杂度为O(1)。 (1)搭建实验环境。在NS-3(network simulator version 3)运行环境中进行程序的仿真工作。根据网络拓扑模型搭建实验环境,如图3所示,在NS-3中创建一个节点作为路由器,n个节点作为实际的存储节点,并在网络链路上配置带宽为1 Gb/s、时延为1 ms,IP地址为10.0.0.x等。这(n+1)个节点可以模拟分布式存储环境,进行实验测试。 图3 网络拓扑模型 (2)以节点负载和修复时间作为实验指标,发生故障的数据块大小、(k,r)编码参数为变化条件,测定Cyclic和Optns相应的数据并绘图。 图4(a)、图4(b)分别表示了节点负载和修复时间随数据块大小改变的变化。图4(c)、图4(d)分别表示了节点负载和修复时间随(k,r)编码参数改变的变化。 设定编码参数(k,r)为(6,3),单位数据量为2 MB,切片大小为32 KB,故障数据块的大小从8 MB变化到128 MB。从图4(a)可以看出,节点负载与数据块的大小成正比,修复的数据量越多,节点的负载越大。相比Cyclic,Optns的负载约减少16.7%,并随着数据块的增大,Optns减少节点负载的优势越大。从图4(b)可以看出,修复时间与数据块的大小成正比,修复的数据量越多,修复时间越长。数据切片的大小固定后,随着数据块的增大,切片个数增加,Optns与Cyclic的修复时间趋于相等。 图4 实验结果 设定故障数据块大小为64 MB,单位数据量为2 MB,切片数s=2048。从图4(c)可以看出,节点负载与k的取值相关,随着k的值从4增加到12,Optns减少负载的比例从25%降低到8%,减少的比例与k的大小成反比。从图4(d)可以看出,修复时间与k的取值相关,但是k的取值不会明显影响修复时间,与修复时间最直接相关的是网络带宽。相比Cyclic,Optns设置空白的时间片段后,增加的修复时间在0.01 s左右,从总的修复时间来看,毫秒级的差异可以忽略不计。 Optns的性能主要与帮助节点个数k相关,随着k的增大,Optns的性能优势逐渐减小。但是,在实际的系统中,为了减少修复代价,会避免选用k值过大的纠删码方案。因此,可以使用Optns作为纠删码修复流水线新的网络传输结构。 为了解决纠删码修复流水线中节点负载不够均衡的问题,本文提出了改进的网络结构Optns。相比原始网络结构Cyclic,Optns构造了更多的流水线路径,平衡了节点的负载,同时,Optns以O(1)的时间完成了修复,保持了修复流水线优秀的修复效率。由于所有的帮助节点均衡的摊分了所有的修复任务,Optns具有最优的负载均衡性。 本文基于纠删码修复流水线的理论框架,只改变了流水线路径,编码方案没有改变,不影响存储效率、容错率、网络带宽、计算复杂度等性能,故没有引入新的修复代价。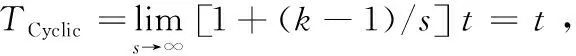
4 实验结果及分析
4.1 实验步骤
4.2 实验结果
4.3 评 价
5 结束语
