基于云模型及粗糙集的民航主数据识别方法

李 国，张 亚，王怀超

(中国民航大学 计算机科学与技术学院，天津 300300)

0 引 言

随着民航业的蓬勃发展，民航数据呈现出指数式的爆炸增长。这些数据中很多是基础的、共享的数据，即某些数据会在多个部门、系统或业务中重复使用。若出现各个部门编码方式不一样或者某个数据在某一个部门更新了，其它部门还未更新等情况，则会造成信息不对称，从而影响最终的决策。因此如何从这些海量的数据中识别出这种具有高价值的、基础的、被多个部门共享的数据，即主数据[1,2]，变得紧迫且重要。

然而，主数据的识别工作一直未受到重视，也未提出比较有效的识别方法，目前的研究有：王学建等[3]提出了基于层次分析法的主数据识别方法,该方法的优点为它是一个系统性的分析方法，简单实用且所需定量数据较少，缺点为定性成份较多，不易令人信服；当指标过多时，数据统计量大，权重难以计算；权重确定为专家打分法，当某个专家更改时，结果可能会波动很大。刘涛等[4]提出了基于综合加权法的主数据识别方法，综合加权法即德尔菲法与主成分分析法的结合，主成分分析法主要思想就是降维，将多指标转化为少数几个综合指标，这几个综合指标代表了原始变量的大部分信息，德尔菲法即专家打分法，该方法的优点为当数据量过大时，通过降维减少数据量，易于计算，缺点是专家打分具有主观性，当替换某个专家时，结果可能波动很大。上述理论和方法在权重确定方面都是由专家打分得到的。这就意味着人为主观因素影响较大。因此，识别主数据仍是一个重大挑战，有必要探索新的有效的理论和方法。

为消除主数据识别指标中的随机性和模糊性，识别过程的关键两点：①用于主数据识别的定性指标的定量化描述。正向云模型方法是一种基于概率论和模糊数学理论的定性概念到定量表示的转化模型，它可以将概念内涵(主观世界中的抽象概念)转化为概念外延(客观世界中的样本集合)。故本文基于此模型，实现主数据识别指标的定量化。②指标权重的确定问题。传统的权重确定几乎都需要专家打分，存在某种程度的主观性。粗糙集理论可以根据客观存在的样本数据来计算各个指标的权重，可以得到相对客观的结果。故本文采用粗糙集的方法来确定指标之间的权重。基于以上两点分析，本文提出了一种基于云模型及粗糙集的民航主数据识别方法。

本文基于云模型及粗糙集的对民航主数据进行识别。考虑到识别指标的模糊性和不确定性，选取7个具有代表性的典型指标建立识别指标体系，通过客观方法得到识别指标的客观权重。然后，基于客观权重建立了RS-CM(粗糙集-云模型)，为民航主数据识别提供了一种方法。

1 相关工作

1.1 主数据的识别指标

民航新一代旅客服务系统由21个子系统组成，根据中国民航的业务特点、主数据的定义及主数据具有的特征一致性、识别唯一性、长期有效性、业务稳定性的特点，在确定主数据的识别指标时，需重点考虑以下因素：

(1)基础性

并不是所有的数据都是主数据，主数据是原子数据，不是衍生数据。如旅客订票后，旅客和机票皆是原子数据，它具有不可拆分性。

(2)共享性

共享性是主数据非常重要的一个特性，是其它特性的前提。主数据一定会被多个系统访问，某个数据被访问的系统越多，则它越可能是主数据。如国家代码会被运价发布和计算系统、电子票系统、货运系统、离港系统、GDS分销系统等共同使用，则国家代码极有可能是主数据。

(3)存在时间

主数据一般存在时间比较长，被多个系统共享的临时数据不是主数据，如机场代码需长期存在，不能缺少，则机场代码可能是主数据。

(4)访问次数

主数据一般比较活跃，被各个系统访问频繁，即需要经常使用到的数据。如城市代码会被离港系统、GDS分销系统、电子票系统等频繁访问，则城市代码极有可能是主数据。

(5)变更频率

主数据一般比较稳定，变动频率较低。如省代码。

充分考虑以上因素，最终确定主数据识别的7个指标，见表1。

表1 主数据识别指标

1.2 云模型

云模型[6-8]是Li和Du[9]在1995年首次提出的一种数学模型。它考虑了定性概念与定量数值表示之间转换的不确定性。充分考虑了主数据的模糊性和随机性。

设Z是一个定量集合Z={x}。C在Z中是定性的概念，确定的参数x∈Z，在C中是随机发生的，对于Z中的任何元素x，C中x的确定性程度为μ(x)∈[0,1]，μ(x)是一个稳定的随机数。x在Z中的分布称为云，每个x称为云滴。由大量的云滴组成的云可以代表领域空间中的定性概念[10,11]。

引入了3个数值特征(Ex、En和He)来表示云模型中的定性概念。期望Ex是区域空间中云滴空间分布的期望和集合的均值，Ex也是最能代表定性概念的点。熵En是由定性概念的随机性和模糊性决定的。具体来说，En是定性的随机性和模糊性的度量的概念。超熵是熵不确定性的一种度量，反映了不确定性在域空间中各点的内聚性。超熵值He间接反映了云滴的厚度[12]。

本文采用正向云发生器和x条件云发生器。正向云发生器具有将定性概念转换为定量值的能力，这些发生器根据云的3个数值特性来生成云滴。x条件云发生器是一种基于云的3个数值特征与x的指定值的组合，能够产生云滴(x，μ(x))的正向云发生器。通过两个发生器的结合，可以得到各种类型的云，在定性知识和定量值之间进行转换[13]。

2 基于云模型-粗糙集的民航主数据识别方法

2.1 基于云模型-粗糙集的民航主数据识别思路

由于主数据具有随机性与模糊性等不确定性特征，故若对主数据进行分等级识别，则得到的结果会更加精确与合理。所以本文借助于云模型理论，根据主数据的特点，选出最能定性概括民航主数据的几个指标，通过这些指标来对主数据进行分级识别。识别过程中，权重的确定尤为重要，本文采用粗糙集理论来确定各指标的权重，这样处理使结果更加客观。具体过程如下：

步骤1 根据主数据特点，选出最具代表性的识别指标，对主数据进行等级划分；

步骤2 对各指标不同等级计算相应云模型的3个参数，生成相应的云模型图；

步骤3 根据民航采集的数据，计算出各等级对应各指标的隶属度u(x)；

步骤4 根据粗糙集理论确定各指标的权重wi；

步骤5 用如下公式计算综合确定性程度

(1)

步骤6 根据最大确定度原理确定主数据的等级。

识别过程流程，如图1所示。

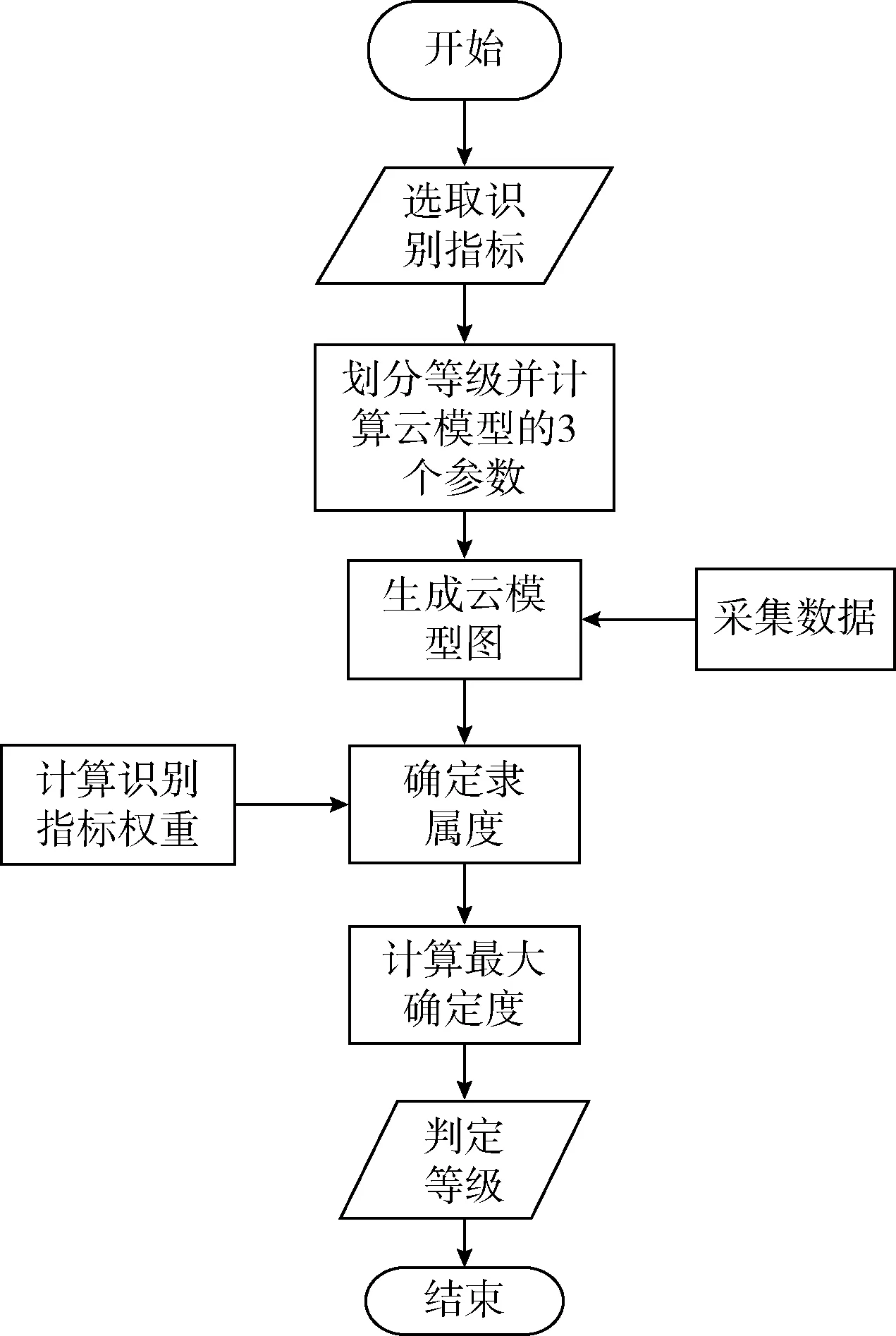
图1 识别过程流程

2.2 分布函数的选择

云模型的具体实现方法有多种形式，依据不同的概率分布可以形成不同的云，比如基于正态分布的正态云、基于高斯分布的高斯云、基于线性分布的线性云等。其中，正态分布广泛存在于社会活动、自然活动、及生产技术中。实际生活中遇到的大部分随机事件都呈现正态分布或者近似呈现正态分布。由中心极限定理可知，正态云模型具有普适性，所以本文选择正态云。

2.3 云模型中参数的计算方法

云模型中3个参数的计算方法[14]如下

(2)

式中：Zmax和Zmin分别为各等级对应的最大值和最小值。r是一个固定值，可以根据变量的模糊度进行调整，在本研究中固定为0.01。

识别过程步骤3中数据x对应的隶属度函数[15]如式(3)所示，因为经过对各类隶属函数进行对比，发现其它隶属函数多数与正态隶属函数一致。它们大部分是正态隶属函数泰勒展开式的低次项之和，是正态隶属函数的近似表达。所以正态隶属函数具有普适性，则本文选择正态隶属函数来确定样本的隶属度

(3)

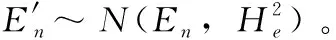
2.4 权重确定方法

粗糙集理论[16-18]是波兰数学家Pawlak提出的一种数据挖掘方法，这种方法挖掘不完整的数据，发现隐藏的信息，它在确定指标权重方面具有独特的优势，可以消除人为因素的影响且它最大的优势是克服了模糊集合论中隶属函数的主观性，属性重要度、条件信息熵等是从原始数据中计算得到的，人不会参与进来，所以用它来确定指标的权重是比较客观的[19-21]。

定义1 在决策表S=(U,A,V,f)中，其中U是非空有限集合，称为论域，记为U={x1,x2,…,xn}；A=C∪D，C是条件属性集，D为决策属性集，C∩D=φ；f:U×A→V是一个信息函数，V=∪Va，a∈A，Va表示属性a的值域。

定义3 在决策表S=(U,A,V,f)中，A=C∪D，指标属性C,U/C={C1,C2,…,Cm}，决策属性D,U/D={D1,D2,…,Dn},则决策属性相对于指标属性的条件信息熵为

(4)

定义4 在决策表S=(U,A,V,f)中，A=C∪D,∀c∈C,a∈A,x∈U,则条件属性c的重要度为

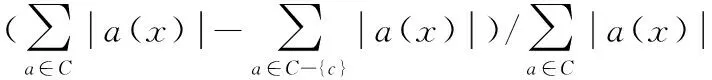
(5)

其中，a(x)=U/{a}。

定义5 在决策表S={U,A,V,f)中，A=C∪D,∀c∈C,则条件属性c的权重为

(6)

3 仿真实验与分析

本节仿真实验的实验环境是：Intel(R) Core(TM)i5-4590CPU，8 GB内存，操作系统为Windows7 旗舰版，在Matlab环境下进行仿真实验。

本节模拟实际场景进行仿真实验，来验证本文研究的基于粗糙集-云模型的民航主数据识别方法的可行性。

本节仿真实验数据皆来自航空公司。

3.1 数据预处理

将主数据划分为5个等级，每个等级代表成为主数据的可能性，具体含义为I(极高)，II(高)，III(中)，IV(弱),Ⅴ(极弱)。由7个指标共同决定，见表2。

表2中，统计了民航信息系统20个月来的数据，每个指标值的含义如下：按照民航信息系统的优先级规则将业务优先级设置为10级；统计数据在系统中的生命周期，以月为单位，比如说国家代码在系统中的生命周期是20个月，则国家代码的生命周期这一识别指标为第一等级；统计数据的标识作用，以百分比为单位；查询该数据被访问的系统个数，最多为17个子系统；统计数据的变更频率，以月为单位；查询一天中数据在系统中的被访问的次数；判断数据的基础性。根据以上分析，生成如表2所示的主数据等级标准。

表2 主数据等级标准

3.2 仿真实验过程

由于正态云具有普适性，故本文使用正态分布函数的正向云发生器。将定性描述的识别指标转化为用3个数字特征表示的定量映射。映射过程由式(2)计算，得到主数据各个指标的云模型参数(Ex,En,He),分别为：

业务优先级：I(9.5,0.42,0.01)， II(8,0.85,0.01)， III(5.5,1.27,0.01)， IV(3,0.85,0.01)， Ⅴ(1.5,0.42,0.01)；

生命周期：I(17.5,2.12,0.01)， II(13.5,1.27,0.01)， III(9,2.55,0.01), IV(4.5,1.3,0.01)， Ⅴ(1.5,1.27,0.01)；

唯一性：I(95,4.25,0.01)， II(77.5,10.62,0.01)， III(50,12.7,0.01)， IV(22.5,10.6,0.01)， Ⅴ(5,4.25,0.01)；

跨系统使用：I(12,4.25,0.01)， II(6,0.85,0.01)， III(4,0.85,0.01)， IV(2.5,0.42,0.01)， Ⅴ(1,0.85,0.01)；

变更频率：I(1,0.85,0.01)， II(3,0.85,0.01)， III(5.5,1.27,0.01)， IV(8,0.85,0.01)， Ⅴ(10.5,1.27,0.01)；

使用频率：I(150,16.96,0.01)， II(115,12.74,0.01)， III(75,21.23,0.01)， IV(35,12.7,0.01)， Ⅴ(10,8.49,0.01)；

基础性：I(8.5,0.42,0.01)， II(7.5,1.27,0.01)， III(4.5,1.27,0.01)， IV(2,0.85,0.01)， Ⅴ(0.5,0.42,0.01)。然后生成各指标的标准云，如图2所示。

图2为7个识别指标的标准云，每个指标中有5个等级。横坐标为各指标的取值，纵坐标为隶属度。以生命周期为例，当生命周期取16时，则第I、II、III、IV、Ⅴ等级的隶属度分别为0.6、0.3、0.05、0、0。

对于隶属度函数的选择，有线性隶属函数、柯西隶属函数、正态隶属函数等，但由文献[22]可知，正态隶属函数在很多领域与其它隶属函数具有一致性，并且广泛应用在各个领域。故本文选用正态隶属函数，由x条件发生器，根据式(3)将采样数据代入图2中各识别指标标准云，得到每个数据各个识别指标的隶属度，这个隶属度具有随机性，但是是一个具有稳定倾向的随机数，故本文对其进行了100次计算并对这100次结果求其平均数，得到其中的业务优先级隶属度见表3。在该表中，展示了各个样本在每个等级下的隶属度。

根据式(4)、式(5)和式(6)计算各指标的权重，得到各指标权重为业务优先级(0.0084)，生命周期(0.0084)，唯一性(0.0105)，跨系统使用(0.0105)，变更频率(0.0105)，使用频率(0.0105)，基础性(0.0105)。

根据式(1)计算每条数据的综合确定度，以最大确定度作为最终主数据的识别等级。结果见表4。

图2 各识别指标标准云

表3 业务优先级隶属度

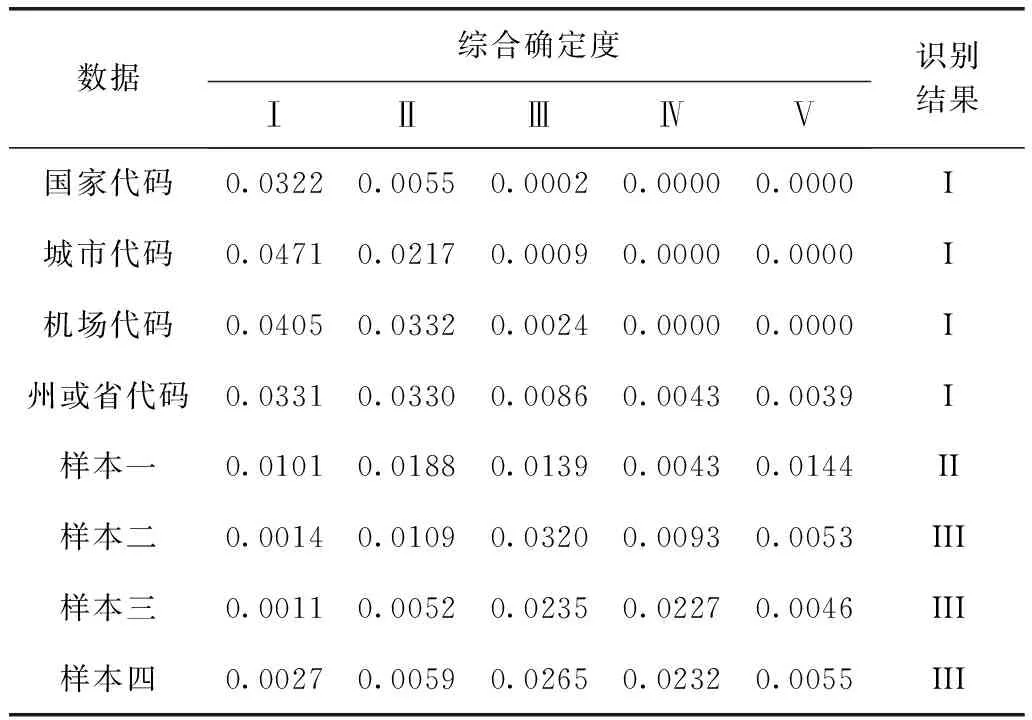
表4 识别结果

3.3 实验结果分析

将表4的识别结果与民航领域已有主数据标准进行对比，国家代码，城市代码，机场代码与州或省代码这4项已经确定一定为主数据，本文识别结果均为Ⅰ等级，故结果合理有效。样本一到样本四与预期结果相同，验证本文研究的主数据识别方法是可行的。

4 结束语

随着社会的高速发展，数据已变成信息时代的重要战略资源，它如同一座有待开采、矿藏丰富的矿山，对它进行有效的挖掘已经成为各个行业的核心竞争力。而对主数据识别则是其中的关键一环。本文依据主数据的随机性与模糊性，提出运用云模型方法对其进行识别，首先选取7个关键识别指标，然后建立标准云模型，再将采集的样本代入标准云模型，求出各个数据隶属于各等级的隶属度。由于每个指标对主数据的影响是不一样的，不能平均对待，故本文采取粗糙集方法来确定各指标的权重。此方法对先验知识要求不高，使权重确定更客观。最后将各隶属度与相应权重结合，求出综合确定度，以最大确定度确定主数据等级。

本文第一次将主数据划分等级，使识别结果更为精确。并且在权重确定这部分与已有方法有很大不同，已有方法人工干预过多，即大多为专家打分，导致结果主观性比较强。本文引入粗糙集方法，根据原始数据计算权重，结果更为客观。将本文所提方法应用在民航领域，最终结果与中航信提供结果一致，验证了本文所提方法的可行性。

但是对主数据识别方法的研究仍然是任重而道远的，还需要进一步的研究。