融合卡尔曼滤波的无人船航向神经网络控制

龚 波，周永华，艾矫燕

(广西大学 电气工程学院，广西 南宁 530004)

0 引 言

近年来，随着科学技术水平的提高，水面无人船(unmanned surface vessel，USV)的应用快速发展，以致其航向跟踪控制问题受到大家的广泛关注。文献[1,2]基于鲁棒稳定性理论分别设计了状态反馈控制器和模糊数字PID控制器，实现了船舶航向的状态保持与控制；文献[3]考虑了系统的建模误差和环境扰动，提出采用径向基函数神经网络(radial basis function neural network)逼近其带来的不确定性信息，设计了一种USV航向跟踪自适应RBF网络控制器；文献[4,5]基于级联系统理论和李雅普诺夫理论设计了非对称模型的欠驱动船航向误差镇定控制器，实现了任意参考轨迹下的USV路径跟踪控制；文献[6]提出一种自适应动态滑模控制方法，使欠驱动无人船对直线和曲线路径具备了良好的循迹性能。

以上文献都是直接从船舶的系统响应模型出发，根据先进的控制理论设计了航向航迹控制方法，设计过程较为复杂。本文考虑控制器的鲁棒性和设计简捷方便的问题，采用系统描述精度更高，控制细节更加灵活的分数阶PID设计无人船航向控制律，并给出一种适用于该控制律的参数自整定神经网络学习算法。此外，为消除环境扰动对USV操纵性能产生的影响，还设计了相应的扩展卡尔曼滤波器，最后通过仿真实验验证了所提方法的可行性和有效性。

1 数学模型

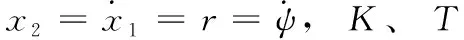
(1)

此外，水上航行时的风浪干扰是引起无人船摇荡和偏航的主要因素，故而在对无人船的航向控制器进行设计时，风浪环境的扰动不可忽略。

对于风干扰，描述为一种舵角干扰信号，仿真时采用白噪声替代，并将其作用于船舶运动控制的舵角指令中以模拟风对USV操纵的影响，该模型描述为

W(s)=Aw(s)

(2)

对于浪干扰，等效为对船舶航向的扰动，仿真时采用白噪声驱动一个典型的二阶振荡环节来模拟[7]，并将其作用于USV的实际航向，该模型描述为

(3)

其中，A为白噪声的增益系数，Kω为海浪模型的增益系数，为海浪的阻尼系数，ω0为主导海浪的频率，w(s)为零均值高斯白噪声。

2 卡尔曼滤波器设计

无人船在水面航行的时候，其运动方向会受到海风和海浪的随机性扰动，而船舶上的传感器设备又无法自动识别这些复杂的干扰信息，进而无法获得船舶的真实航向。尤其是遇到大强度高频率的扰动，无人船的航向控制难度会进一步加大。这些情况会最终表现为船舶的航向信息无规则振荡，而偏航信息振荡会使USV的舵机进行频繁的动作，轻则发生机械损伤，影响舵机的使用寿命，重则能危及航行安全，引发严重的航海事故。本节就是针对这种情况设计出相应的卡尔曼滤波器，以滤除USV在水面航行过程中的环境噪声，避免它们对于USV舵机操纵的不利影响。

工程中，卡尔曼滤波应用广泛，但它必须在计算机上执行，因此需要知道被控对象的离散化数学模型。在风浪干扰仿真模型的基础上，本文取采样周期h为小于式(1)所给系统的最小时间常数1/10的较小值，根据一阶导数的前向差分离散化定义可将该连续系统近似离散化为

(4)

此时，式(4)为含有风干扰信号(过程噪声)w(k)和浪干扰信号(观测噪声)l(k)的USV航向控制系统非线性离散化数学模型。

但单纯的卡尔曼滤波方法只适用于线性系统，而本文所给的无人船航向控制系统为非线性系统，所以这里需要在Bucy等提出的扩展卡尔曼滤波(extended Kalman filter, EKF)方法框架下进一步设计USV航向跟踪控制系统的扩展卡尔曼滤波器[8]。假若定义风浪干扰的白噪声方差分别为R和Q，EKF的具体设计步骤为：

(1)USV初始状态X(0)，即无人船航向和转艏角速度以及协方差矩阵P0的初始化；

(2)状态预测：由USV的第k-1次状态X(k-1|k-1) 预测第k次状态X(k|k-1)；

(3)观测预测：根据状态预测量X(k|k-1) 计算第k次的观测预测值Y(k|k-1)；

(4)一阶线性化状态方程和观测方程，求解状态转移矩阵F(k)、控制矩阵B(k)和观测矩阵H(k) 分别如下

(5)

(6)

(5)先验估计误差的协方差矩阵P(k|k-1) 计算

P(k|k-1)=F(k)P(k-1|k-1)FT(k)+B(k)QBT(k)

(7)

(6)求卡尔曼滤波增益

(8)

(7)USV状态向量更新

X(k|k)=X(k|k-1)+K(k)(Y(k)-Y(k|k-1))

(9)

(8)协方差更新

P(k|k)=(In-K(k)H(k))P(k|k-1)

(10)

以上8个步骤为USV航向控制滤波器的一个计算周期，而对这个计算周期不断循环的过程即是各个时刻EKF对航向非线性系统的处理过程。

3 神经网络分数阶控制器设计

PID控制是日常工程领域里一种使用较为频繁的控制方法。而分数阶PID控制器就是由整数阶PID控制器的积分项和微分项阶次λ和μ由整数领域扩展到分数领域而产生的一种广义PID控制器。在该类控制器的工程应用过程中，考虑到分数阶控制器具有良好的全局相关性，对非线性系统的描述更为精确，且具有更高的控制精度，所以本文考虑引入分数阶控制理论设计USV航向跟踪控制指令δ的控制律为

(11)

式中： 0<λ，μ<2，kp、ki和kd为控制器参数，D为微积分算子，e(t) 为USV航向误差。在时域范围内，可通过Grunwal-Letnikov定义，对式(11)进行时间离散化[9]。

Grunwal-Letnikov分数阶导数定义为

(12)

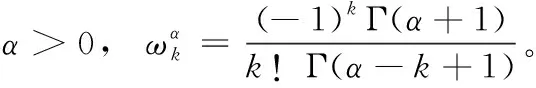
取时间步长为h，对式(12)去极限后进行z变换，可推式(11)的时间离散表达式为

(13)

RBF神经网络是一种三层前向网络，具有较强的函数逼近能力，算法简单，运行速度快，甚至能够避免类似BP网络中的局部极小问题，非常适用于实时控制的系统[10]。实现RBF神经网络整定分数阶PID控制器参数的原理框架如图1所示。

图1 RBF网络整定控制器参数原理框架

由图1可知，本文所设计的控制器由3部分组成：①分数阶PID控制器：直接对船舶航向进行闭环控制，给出USV舵角指令跟随偏航误差在线调整的控制律；②扩展卡尔曼滤波器EKF：滤除系统噪声，估计船舶航向的真实值，保证无人船操纵性能；③RBF神经网络：根据系统运行状态在线调整网络参数(中心点向量、基函数宽度和网络权值)进行自我训练，使其稳定状态对应于所给最优控制律下的分数阶PID控制器参数。也就是说同其它智能优化算法一样，给定一个RBF网络需要优化的系统性能指标函数；当RBF网络状态稳定时，其输出对应于该性能指标函数趋于收敛时的控制律系数，即分数阶PID控制器的5个可调参数。

实现RBF神经网络整定分数阶PID控制器参数的自调整学习算法如下[11]：

(1)控制器参数调整策略

神经网络整定指标取为

(14)

采用梯度下降法计算分数阶控制器的参数修正量，公式如下

(15)

(16)

(17)

(18)

(19)

(2)Jacobian信息辨识算法

RBF神经网络的结构选为3-6-1，令i(i=1,2,3) 为输入层结点数，j(j=1,2,…,6) 为隐含层结点数。网络辨识的3个输入为X=[δ(k),ψ(k),ψ(k-1)]T， 网络的第j个结点的中心矢量为Cj=[cj1,cj2,cj3]T， 高斯基函数的宽度向量为 [b1,b2,…,bj,…,b6]T， 网络权向量为 [w1,w2,…,wj,…,w6]T， 径向基向量为 [h1,h2,…,hj,…,h6]T， 其中hj为高斯基函数

(20)

定义RBF神经网络辨识的输出为ψn(k)， 无人船实际航向为ψ(k)， 辨识器的性能指标函数取为

(21)

同样采用梯度下降法，对网络权值、基宽向量和中心矢量进行增量计算

(22)

(23)

(24)

USV输出航向对舵角指令变化的Jacobian信息计算表达式为

(25)

(3)参数调整的加速策略

通过对控制器和RBF网络的参数进行合理的调整，可促进网络学习的效率，保证无人船航向跟踪控制的快速性，这里从RBF网络的学习速率和控制器参数修正步长两个方面来说明。

首先可调的参数为RBF神经网络的学习速率，它代表了神经网络在时间推移的过程中，自身信息的累积速度。学习速率若是设置太低，网络的训练进展也会比较缓慢，其所耗费的时间也就会延长；反之，学习速率若是设置太高，网络的训练就可能会产生较不理想的结果，而通常较为普遍做法是选取学习速率随训练进度由高到低取值[12]。考虑到本文的实际应用情况，对于参数p(p为kp、ki、kd、λ、μ)，在设定修正步长为Δp(k-2) 时，记录USV的航向误差为e(k-1)， 在修正步长取Δp(k-1) 时，记录USV的航向误差为e(k)，比较e(k-1) 和e(k)，若航向误差逐渐减小，说明参数更新的方向正确，可以适当的增加RBF网络的学习速率，让其乘以增量因子kinc；反之，若航向误差逐渐增加，说明参数修正过头，应适当的减小学习速率，迫使其学习速率乘以减量因子kdec，也即是说

(26)

其次，在航向控制系统工作的过程中，参考信息越多，系统调整的速率越快，若同时考虑Δp(k-2) 和Δp(k-1) 两次修正量的符号以及e(k-1) 和e(k)两次航向误差的变化情况，则可以给出控制器参数更高质量的第k次修正步长。设控制器参数p的第k次修正量为cp(k)，则第k次修正步长p(k)=p(k-1)+cp(k)， 当Δp(k-2) 和Δp(k-1) 两次修正量的符号相同时，若误差减小，则将Δp(k-2)、 Δp(k-1) 和Δp(k) 作正向的线性叠加，反之则作负向的线性叠加；当Δp(k-2) 和Δp(k-1) 两次修正量的符号相反时，若误差减小，则将Δp(k-1) 和Δp(k) 作正向的线性叠加，反之取Δp(k-2) 和Δp(k) 进行线性叠加。令惯性因子为ρ，代表每一次线性叠加的过程中，步长参考Δp(k-2) 和Δp(k-1) 两次修正量信息的多少程度，得到参数p的第k次修正量cp(k)的取值公式见表1。

表1 修正量cp(k)取值计算方法

4 仿真实验

选取某USV船模进行仿真实验，其具体参数为K=1，T=2，非线性系数α=0.5，考虑舵角的机械饱和限制条件：-35°≤δ≤35°控制器参数中的学习率初值η=0.3，增量因子kinc=1.2，减量因子kdec=0.7，仿真中的时间采样周期h=0.01s，修正量惯性因子ρ=0.9。仿真实验在Matlab/Simulink软工平台上进行。

仿真实验1：无环境扰动下，系统(1)和系统(4)的仿真对比实验。系统(1)即式(1)所示的连续型USV航向跟踪控制系统，系统(4)即该连续型系统经离散化后所得的离散型控制系统，如式(4)所示。在常规PID控制器作用下，分别取控制器参数为：kp=4，ki=1，kd=3，设置实验过程中的期望参考航向以40 s为周期做±10°的交替变换，在100 s内得到两个系统的航向控制响应曲线如图2所示。

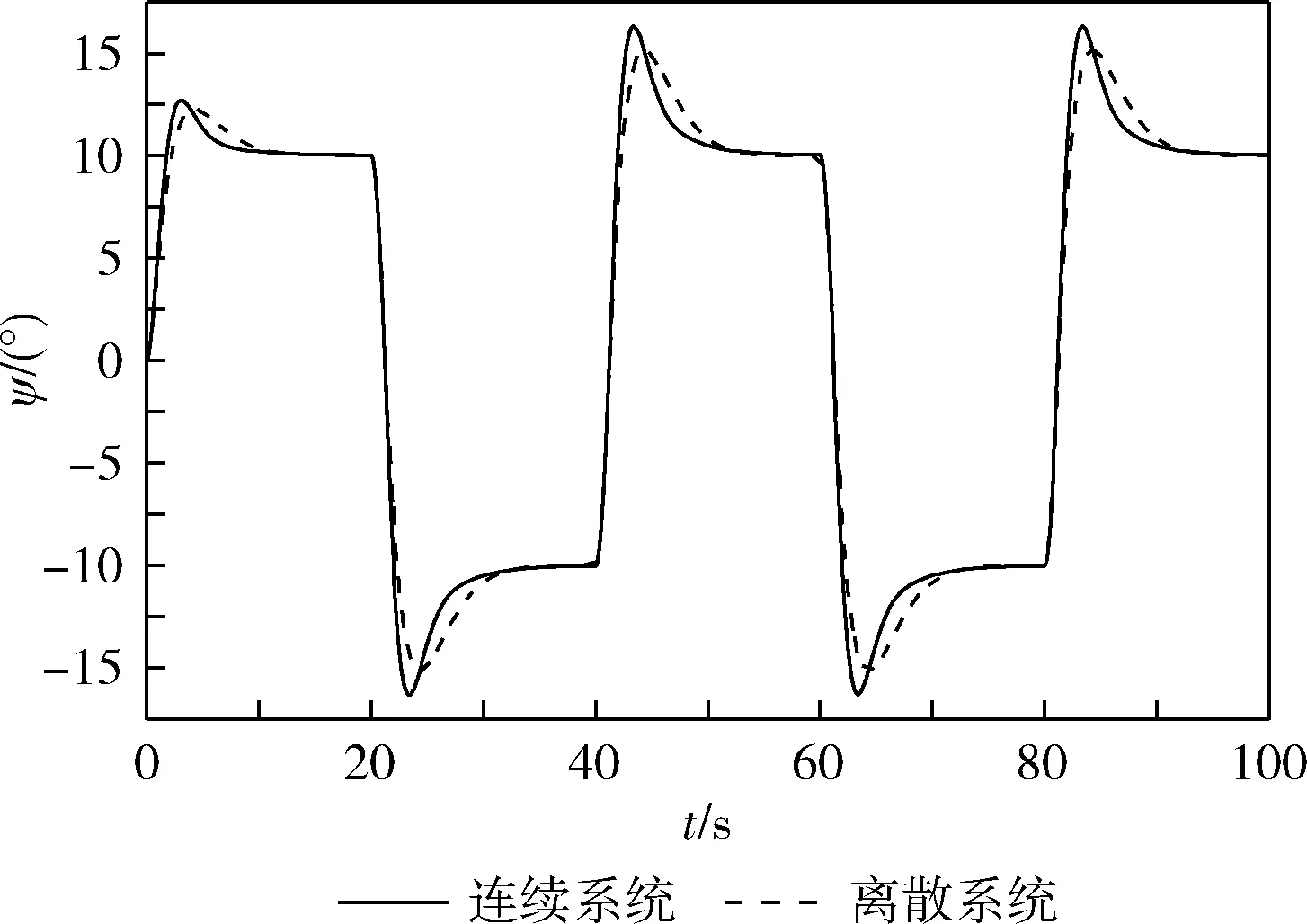
图2 两种系统下的航向响应曲线

由图2可知，在被控对象、实验背景和控制方式相同的情况下，离散型USV航向跟踪控制系统和连续型USV航向跟踪控制系统的航向响应曲线除超调量有少量不同以外，其上升时间和调节时间基本一致，且两条航向响应曲线的走向总体相同，说明了本文对连续型USV航向跟踪控制系统(1)所采用的近似离散化方法有效可行。

仿真实验2：无环境扰动下，常规PID控制器、模糊PID控制器、RBF神经网络PID控制器和本文方法的仿真对比实验。分别取各控制器的初始参数值为：kp=4，ki=1，kd=3，λ=1，μ=1，设置实验过程中的期望参考航向以40 s为周期做±10° 的交替变换，在60 s内得到离散系统(4)的航向控制响应曲线如图3所示。

图3 不同控制器作用下的航向响应曲线

根据图3可以发现，模糊PID控制器和常规PID控制器的控制结果较不理想，主要体现在调节时间较长，超调量较大；而比较之下的RBF神经网络PID控制器和本文方法基本做到无静差调节，调节速度快而且精度高。同时还可以发现在所比较的4种方法中，本文所设计的控制方法具有最快的调节速度和更好的控制品质。

仿真实验3：有环境扰动下，不含EKF的RBF神经网络分数阶控制器、含有EKF的RBF神经网络分数阶控制器和模糊PID控制器的仿真对比实验。根据式(2)和式(3)，本文选取风扰动模型为均值等于0，增益等于0.1，方差等于1的高斯白噪声信号；选取海浪干扰模型的传递参数Kω=0.4198，=0.3，ω0=0.60625，其激励源是功率谱密度为0.01的高斯白噪声，以上参数设定基本能够模拟该USV可能遭遇的较危险环境。另取控制器各初始参数为：kp=4，ki=0.1，kd=3，λ=1，μ=1，设置实验过程中的期望参考航向以40 s为周期做±10°的交替变换，在60 s内得到离散系统(4)的航向响应曲线和舵角指令曲线分别如图4和图5所示。

图4 不同控制方式下的航向响应曲线

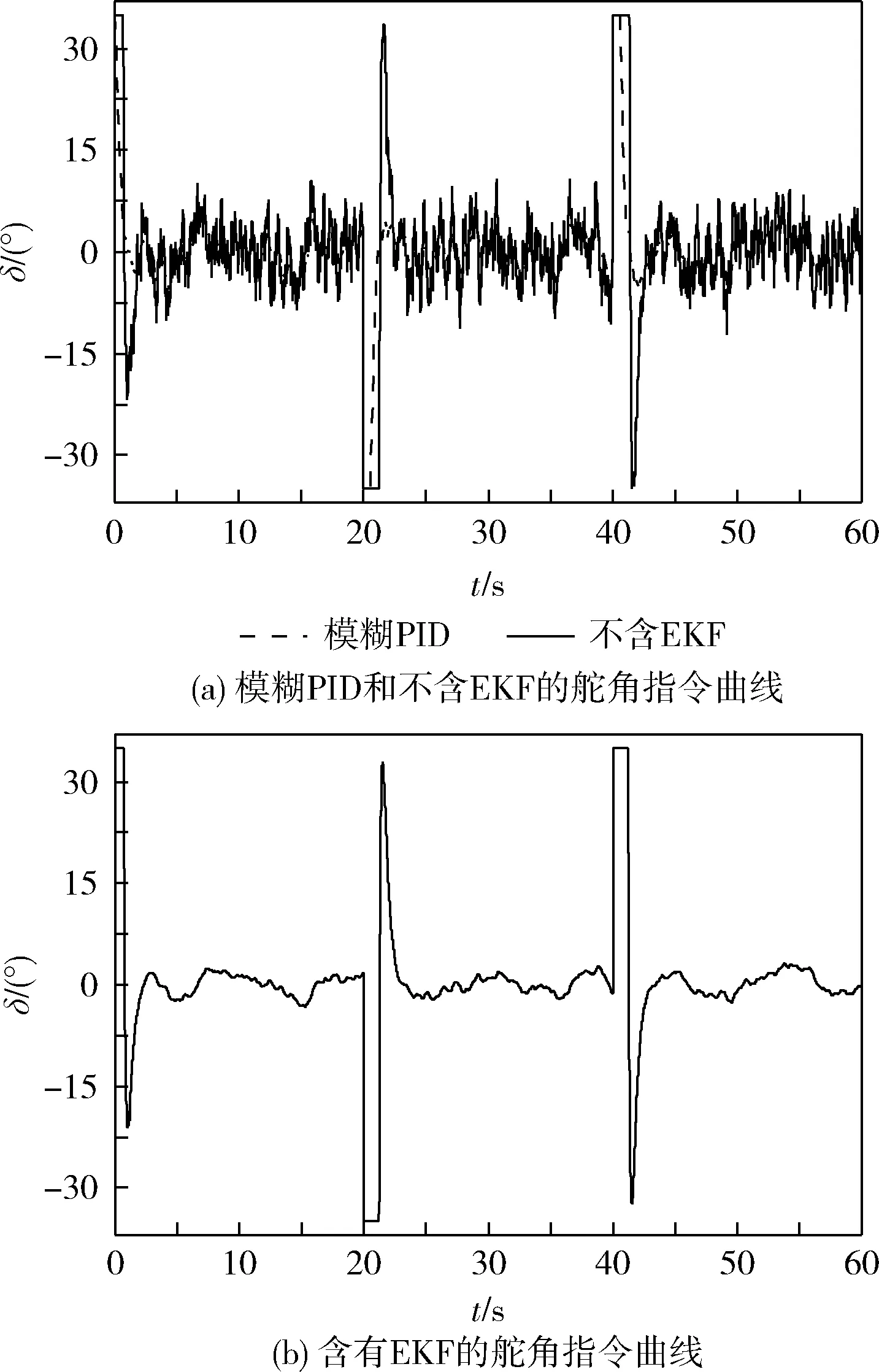
图5 不同控制方式下的舵角指令曲线

由图4可以看出，当采用RBF神经网络分数阶控制器对USV的航向进行控制时，扩展卡尔曼滤波器并不影响其航向控制的实际结果。因为，在不含EKF和含有EKF的情况下，RBF神经网络分数阶控制器对USV的航向均做出了有效控制，体现了较强的鲁棒性，在控制效果上也明显优于模糊PID控制器，其调节速度快而且稳态精度较高。

由图5可以看出，扩展卡尔曼滤波器对船舶舵机的操舵影响比较明显。在不含EKF时，RBF神经网络分数阶控制器和模糊PID控制器作用下的操舵指令均出现了高频率大范围的振荡，这是一种非常不合理的操舵现象。因为船舶在水面航行时，环境干扰是长期存在的，而频繁的操纵船舶舵机，长期以来会对舵机产生机械损伤，从而影响船舶的使用寿命，严重的甚至于危及水上航行安全。但在分数阶控制器中引入扩展卡尔曼滤波器以后，不仅保证了分数阶控制器更好的航向跟踪控制品质，而且使得无人船舵机响应为一条连续接近光滑的曲线，没有出现高频率大范围的振荡，有效保护了舵机结构，是一种较为理想的操舵方式。

5 结束语

针对无人船航向跟踪控制系统，有效结合了卡尔曼滤波器和径向基函数神经网络的优点，设计了RBF神经网络分数阶航向控制器。其中，RBF神经网络解决了控制器参数的整定问题，卡尔曼滤波器的引入避免了舵机响应高频率大范围的振荡，分数阶PID和RBF神经网络的结合保证了USV的航向控制质量。最后通过仿真对比实验，验证了本文所提出的航向控制方法较常规PID控制器、模糊PID控制器和RBF神经网络PID控制器具有更好的调节品质：船舶航向跟踪稳定，抗扰能力强，调节速度快，在有环境扰动的情况下也能保证较强的自适应性和鲁棒性。