基于Logistic 映射的射频识别防碰撞算法

刘 艳 ，张 玉 *

（1. 大连市环境感知与智能控制重点实验室（大连大学），辽宁大连116622； 2. 大连大学信息工程学院，辽宁大连116622）

0 引言

射频识别（Radio Frequency IDentification，RFID）标签具有体积小、成本低、易于处理等优点，目前被广泛应用于仓库管理、物流控制、智能货架、产品追踪等领域［1-2］。实际应用中，当两个或多个标签同时与阅读器通信时，信号将互相干扰，产生标签碰撞问题，导致标签的识别准确率、速度和效率等性能变差，标签防碰撞算法成为当前RFID系统亟待突破的关键技术之一［3］。

目前，标签防碰撞算法主要有两种：基于树的算法和基于Aloha 协议的算法［4-8］。在大型 RFID 系统应用中，标签群体很大，二叉树算法的复杂度较高、延迟较长，无法满足识别环境中实时识别的要求［9］。因此，基于Aloha协议的算法被广泛采用，该算法简单、使用成本低。文献［10］中证明了在Aloha 算法中，当标签数与帧长度相等时，系统最高吞吐量理论上可达0.368，帧长大小的选取对系统吞吐率高低起着十分关键的作用。文献［11-12］中分别在基于Q 值算法和动态帧时隙Aloha（Dynamic Framed Slotted Aloha，DFSA）算法的基础上，对标签识别过程进行了优化，使系统吞吐量大于0.6。文献［13］中结合了Aloha 和树类算法的优点，首先利用DFSA 算法对标签进行识别，然后通过最大碰撞位判断将剩余标签分为左右子树，实现对部分碰撞标签的成功识别，使系统吞吐量进一步提高到0.7。

传统DFSA 算法基于标签与时隙的一对一识别，系统吞吐量始终较低。为了解决这一问题，可并行识别方案被广泛研究并使用［14-15］，它们突破了一个时隙只能识别一个标签的束缚，可以大幅度提高标签的吞吐量。Buzz 算法［16］借助压缩感知概念来稀疏碰撞信号、解码标签信息、减少碰撞标签；但它依赖于信道估计，当同时传输的标签数量超过100 时，Buzz算法的计算复杂性显著增加，在涉及大量标签的应用环境中效率更低。并行识别协议（Parallel Identification Protocol，PIP）算法［17］使用L-K 代码进行识别，它用一个特殊设计的模式将标签ID 编码成一个位字符串，实现标签并行识别；但是PIP算法中读写器必须已知整个标签集，这在真实使用场景中不可实现。文献［18-19］中提出了基于正交可变扩频因子（Orthogonal Variable Spreading Factor，OVSF）码的并行识别方案，该方案将扩频通信技术和DFSA 算法相结合，扩频通信技术的应用，实现了标签的并行识别，提高了系统吞吐量；缺点是伪随机码的个数有限，并且每个标签必须存储2n(n =1，2，…)个扩频码，缺乏灵活性，且占用大量的标签内存资源。文献［20］中将快速独立成分分析（Fast Independent Component Analysis，FastICA）技术与DFSA 算法结合，提高了算法吞吐量，但要求阅读器天线数为8。显然，上述标签识别方案均未涉及标签完全识别的判断标准，无法解决某一标签始终不能被识别而导致的标签“饥饿”问题［21］。

针对上述问题，本文提出了基于Logistic 映射的DFSA（Logistic-DFSA）算法。该算法利用Logistic 映射可以产生数量巨大序列的优点，将Logistic 映射引入扩频通信技术中［22］，满足大容量识别系统的需求；同时，因为Logistic 映射可以根据需要产生随意码长序列，且每个标签仅需存储一个扩频码序列，避免了OVSF 码的灵活性差和占用大量内存的缺点；将扩频通信技术与DFSA 算法结合，突破了Aloha 算法碰撞时隙中无法识别标签的限制；通过帧长、扩频码长度和标签数量对系统识别过程中吞吐量的影响变化的研究，确定最优帧长、扩频码长度；根据一帧结束后剩余标签数量，给出标签可完全识别的重复帧算法。最后，通过仿真实验验证本文算法用于标签识别时，具有需要较少总时隙数、系统吞吐量较高、标签识别率可达100%的优势。

1 Logistic-DFSA算法

本文基于扩频通信技术解决Aloha 算法中一个时隙只能识别一个标签的瓶颈问题，将Logistic 混沌映射应用于扩频通信中，解决扩频码序列数量有限的问题；在标签识别吞吐量分析基础上，确定最优码长与帧长；利用重复帧算法进行标签完全识别。

1.1 改进的标签识别算法

图1 为本文可并行识别标签的方案与传统动态帧时隙Aloha 算法识别标签方案的对比。其中，Frame 为标签识别帧，Slot 为标签选择通信时隙，Tag 为标签号。第一帧识别结束后，存在未成功识别标签，需要开始新的一帧（即第二帧）继续识别，直至所有标签识别完毕。

图1（a）为传统动态帧Aloha 算法，标签只有在成功时隙（只有一个标签的时隙，如图1（a）的Frame1中slot1）中才可成功识别，导致每帧识别结束后，仍有大量未识别标签，需要多帧才能完成标签的全部识别，系统吞吐量较低。本文采用的扩频通信技术的可并行标签识别方案中因为应用了扩频技术，碰撞不再只是简单的多标签选择同一时隙碰撞，而是如图1（b）中所示，标签识别时隙分为四种：

1）成功时隙：只有一个标签的时隙或者一个时隙中的多个标签选择互不相同的扩频码序列，标签可成功识别，如图1（b）的 Frame1 中 Slot4 的 Tag9，Frame2 中 Slot1 的 Tag1、Tag2、Tag6。

2）部分碰撞时隙：多个标签，但是存在码不同标签，此标签可被成功识别，如图1（b）的Frame1中Slot3的Tag4、Tag6。

3）完全碰撞时隙：大于等于2 个标签的时隙且所有标签的扩频码相同，如图 1（b）的 Frame1 中 Slot1 的 Tag1、Tag2、Tag7。

4）空时隙：没有标签的时隙，如图1（b）Frame1中Slot2。

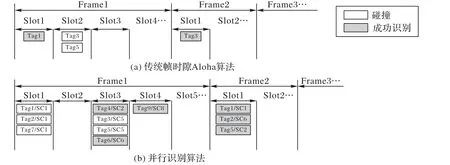
图1 传统帧时隙Aloha算法与并行识别算法对比Fig. 1 Comparison of traditional framed slotted Aloha algorithm and parallel identification algorithm

1.2 伪码序列生成及分析

扩频通信技术广泛应用于信息通信中，生成扩频序列方式的选取十分重要。m 序列、Gold 序列是常用的扩频通信序列，但是当RFID 系统中标签数量较大时，这些序列的数量远远满足不了大容量系统的要求。沃尔什矩阵和OVSF 序列由哈达玛矩阵产生，也经常用于扩频通信，但是每个标签需要存储的扩频码序列数量为2n(n = 1，2，…)，产生扩频码速度过慢，占用过多标签存储空间。

混沌理论生成伪随机数方式简单、快速且易于实现，已被广泛应用于各个领域。每个标签根据初值不同迭代一个对应长度序列，用于扩频通信。常用混沌映射有Logistic 映射、Tent 映射、Henon 映射、Chebyshev 映射、组合混沌映射等。本文选取Logistic 映射生成伪随机数，因为与其他几种混沌映射相比，它具有较好遍历性、自相关和互相关性。Logistic 混沌映射表达式描述为：

其中：xn∈ (0，1)；α是系统控制参数。当α ∈ [3.57，4]时，系统为混沌状态。α = 4 时，称为满映射（函数曲线取满了值域空间）。n为迭代次数，xn表示系统在给定初值之后迭代了n - 1次的状态值。为映射整个迭代空间，本文选取满映射混沌状态，即α = 4。Logistic混沌映射具有如下性质：

1）序列概率密度：

其中ρ(x)与初始值x0无关，所以该系统具有普遍性。

2）序列均值：

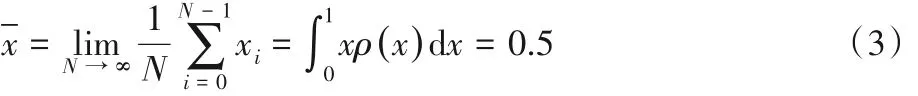
3）自相关函数：

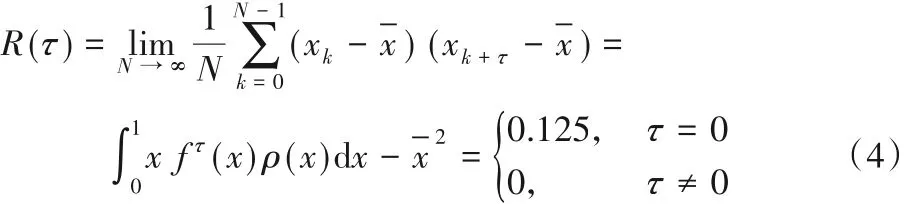
4）互相关函数，其中，初值分别为x10、x20：

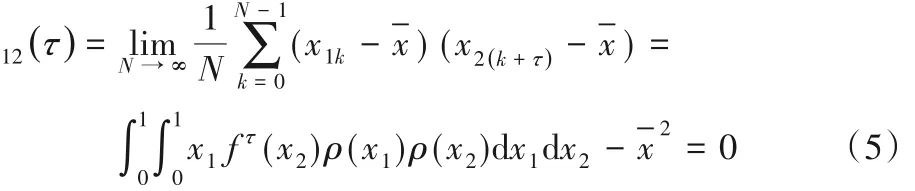
由上述分析可知，Logistic 映射具有良好的自相关和互相关性能，能够应用到扩频通信中，且Logistic 映射根据选取初值不同可迭代出大量序列，因此，可以满足大容量系统的要求。

1.3 码长选取

传统DFSA 算法基于标签与时隙的一对一识别，出现大量碰撞时隙，系统吞吐量较低，本文引入的扩频通信技术，改变了这种关系，可以大幅度提高系统吞吐量，改变这种关系的关键是标签码长的选取。

初始帧长为F，标签数为N，扩频码长度为m时，可用作扩频码的混沌序列的数量为M。假设所有时隙均为碰撞时隙，利用平均分配原则，每个时隙中的标签数为：

扩频码数量为M时，一帧中可以识别的标签数量为：

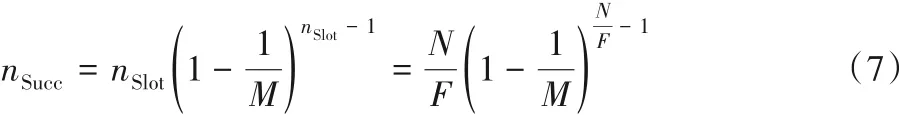
标签识别时，通常情况下选取初始帧长F = 8，则标签数N与扩频码数量M对可识别标签数nSucc的影响如表1所示。

由表1可知，M = 16时，当标签数N = 528，没有标签能被成功识别；M = 32 时，当标签数N = 1296，没有标签能被成功识别；M = 64 时，当标签数N = 3 085，没有标签能被成功识别。一帧中没有标签能被成功识别，即帧中时隙全为完全碰撞时隙，浪费了一帧的同时，将直接影响下一帧最优帧长的选取，应避免这种情况的发生。

1.4 帧长选取

基于1.3 节中的条件，某个时隙能够识别n 个标签的概率为：

n个标签出现在一个时隙中的概率为：

结合式（8）和（9），当前识别所有标签的系统吞吐量为：

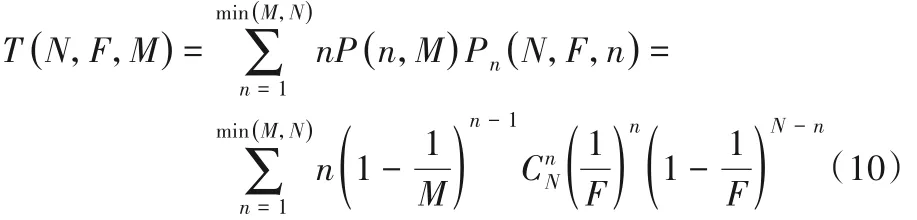
当M ＞ 2时，式（8）可表示为：

对式（11）中的F求偏导，求驻点，得到：

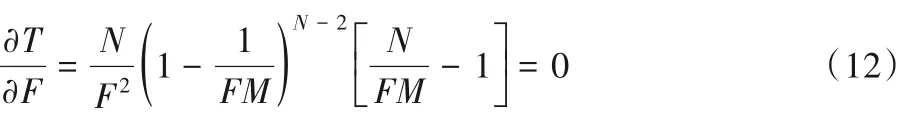
化简得，N = FM 为唯一驻点：当F ＞ N M 时，T(N，F，M)单 调 递 减 ；F ＜ N M 时 ，T(N，F，M) 单 调 递 增 。 函 数T(N，F，M)的最大值为：

因此，N = FM可作为识别标签时的帧长选取依据。文献［10］证明DFSA 算法的最大系统吞吐量为e-1，所以由式（13）可知，本文算法系统吞吐量最大值为DFSA算法的M倍。

本文以被普遍看好的无源标签智能仓储环境为例，实际应用中仓储货架一般在1～2 m，而无源RFID 的感应范围在60 cm左右，因此在阅读器有效识别范围内存在的标签数量是有限的（＜2 000 个），本文假设估计算法估计的标签数量最大值为2 000。图2 为本文算法在标签数N ∈(1，2 000)时，对应不同帧长F和扩频码数量M 下的系统最大吞吐量。可以明显看出，扩频码数量M 越大时，随着帧长增加，系统吞吐量下降越快，所以，帧长过大时，将失去扩频通信应用于DFSA 算法的优势。

图2 最大期望吞吐量与M及F的关系(N ∈(1，1024))Fig. 2 Relationship between maximum expected throughput and M and F(N ∈ (1，1024))

1.5 标签识别结束标准

基于Aloha 防碰撞算法中，标签随机选取时隙与阅读器通信，可能存在某些标签始终无法选取时隙的情况，从而出现标签“饥饿”问题，即识别周期中可能存在始终无法识别的标签，因此，有必要确定是否已成功识别所有标签，以终止标签识别。

理论上，基于Aloha 防碰撞算法可以根据帧内成功识别的标签数量或根据是否有标签回复来决定是否终止识别周期。Aloha防碰撞算法中，识别标签数量等于真正标签数量时终止识别；或者开始新帧时，回复的时隙中只有空时隙，则判定标签完全识别。但RFID系统实际应用场景中，标签数量是未知的，需由标签估计算法确定，标签数量较大时，估计误差也随之增加，此时上述方法已不能确定是否结束标签识别；另外，回复时隙中可能都为空闲时隙，因为没有标签选取通信时隙，但是却有标签未被识别。为了解决上述问题，本文提出了以下重复帧算法。

假设估计的标签数量为n^，每轮阅读器识别的标签数量为Ni(i= 1，2，…)，那么终止标签识别判断如下：

步骤1 假设现在识别结束帧为第i帧，统计每次识别结束剩余标签数量ni=ni-1-Ni（其中i= 2，3，…，n1=n^）。

步骤2 如果ni= 0 或者ni＜0，广播QueryAdjust（Fi），进入步骤1；如果ni= 0，并且已重复过QueryAdjust（Fi），则执行步骤4；如果ni＞0，并且连续两帧没有标签回复，执行步骤4；否则，请继续执行步骤3。

步骤3 开始一个新的识别帧。

步骤4 结束识别周期。

1.6 算法流程

本文所提Logistic-DFSA 算法识别标签流程如图3 所示。其中，F为帧长，m为码长，SN为标签选取通信时隙，SC为标签选取扩频码。

图3 Logistic-DFSA算法流程Fig. 3 Flowchart of Logistic-DFSA algorithm

2 仿真与结果分析

为验证标签识别算法的性能，本文从阅读器识别所有标签所需帧数、总时隙数和系统吞吐量三个方面，利用Matlab仿真软件对 DFSA［8］、CSP-FSA（Continuous Slot Prediction-Frame Slot Aloha）［11］、DFBT（Dynamic Framed Binary Tree）［13］、OVSFDFSA［19］算法以及本文改进的基于Logistic 映射的动态帧时隙Aloha 算法（Logistic-DFSA）进行了仿真实验对比，初始帧长F初始= 8，本文算法选取码长m= 31，可用于扩频通信的序列数量为M= 64［23］，OVSF 码长m= 32，可用于扩频通信的序列数量为M= 32，标签样本数量最大为2 000，以50 为间隔，每个样本数量取50次仿真结果平均值。

2.1 帧数

图4 所示为识别所有标签所需帧数对比。DFSA 算法因为标签与时隙的一对一识别，碰撞标签数量较多，需要较多帧识别全部标签；CSP-FSA 算法通过连续帧状态的预测，可以跳出识别效率较低帧，重新开始新的一帧，增加了识别帧数；DFBT 算法中，通过二进制搜索树算法对未识别标签进行分裂，实现部分碰撞标签成功识别，减少下一帧将要识别的标签数量，从而减少识别标签所需帧数；OVSF-DFSA 算法和本文Logistic-DFSA 算法中，帧长选取为DFSA 和DFBT 算法的1/M，但是扩频通信技术的应用，识别标签帧数仍有较大优势。本文Logistic-DFSA 算法在相同码长的情况下，相比OVSF-DFSA算法，拥有更多的扩频码数量，所以识别标签所需帧数更少。

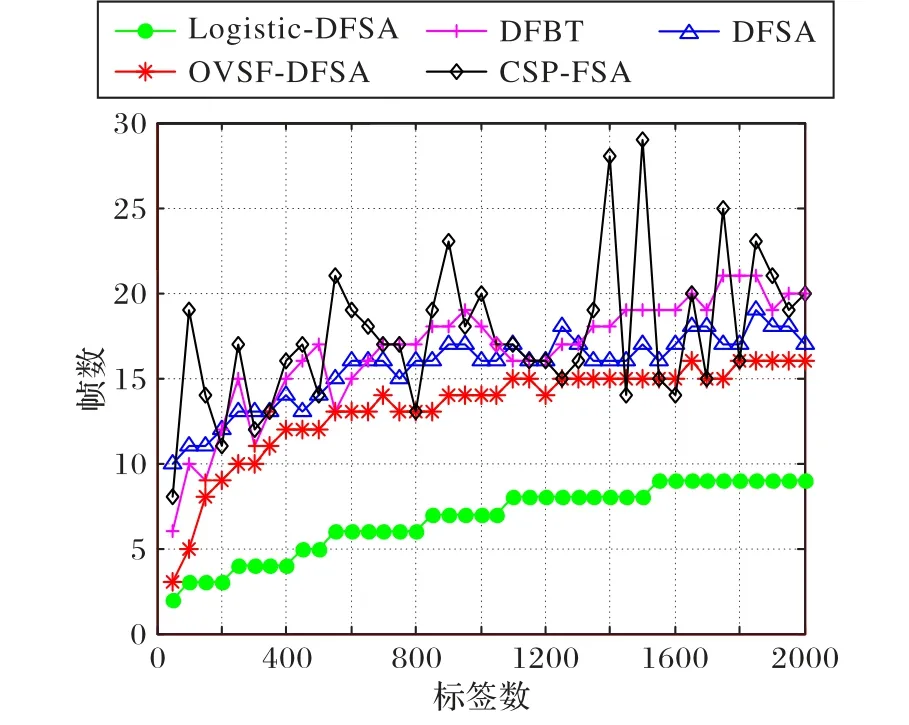
图4 不同标签数时各算法识别标签所需的帧数对比Fig. 4 Comparison of frames of each algorithm for identifying different numbers of tags

2.2 总时隙数

总时隙数为标签识别时系统所需要的成功时隙数、碰撞时隙数、空时隙数总和。防碰撞算法的目的是减少碰撞时隙数和空闲时隙数，提高成功时隙数，但传统的DFSA 算法只能在一个时隙中识别一个标签，碰撞时隙数量较多，所以传统DFSA 算法需要较大帧长和多帧识别标签，导致总时隙数较大；CSP-FSA 算法通过时隙预测机制，可以跳出无效时隙，避免了无效时隙的浪费，识别标签总时隙数有所减少；DFBT 算法中，通过帧时隙Aloha 算法识别和碰撞标签的分裂树识别，减少了下一帧需要识别的标签数量，所以总时隙数相比传统DFSA算法较少。在本文算法中，由于一个时隙可以识别的标签数量由码长控制，当码长选取合适数值时，可以将碰撞时隙中的标签完全识别，从而将碰撞时隙转化为成功时隙，或者识别碰撞时隙中部分标签，将完全碰撞时隙转化为部分碰撞时隙，所需总时隙数大幅减少。如图5 所示，当标签数为2 000时，本文所提算法相较于DFSA、CSP-FSA、DFBT、OVSF-DFSA算法总时隙数分别减少98.3%、97.2%、96.7%、48.3%。由此可见，阅读器与标签之间的通信次数与通信量大幅减少，Logistic-DFSA算法用于标签识别时，复杂度较低。

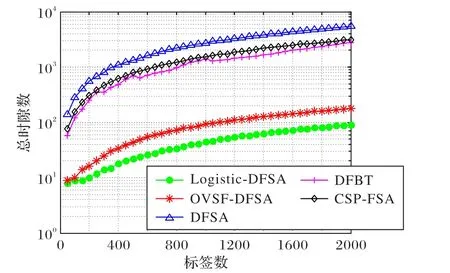
图5 不同标签数时各算法的总时隙数对比Fig. 5 Comparison of total number of slots of each algorithm with different number of tags

2.3 吞吐量

系统吞吐量是标签识别时最重要的衡量系统效率的指标。系统吞吐量T 的定义为可识别标签数N 与所需总时隙数S比值，即T = N/S。

图6 所示为标签数与吞吐量对比，本文Logistic-DFSA 算法和 OVSF-DFSA 算法相较于 DFSA、CSP-FSA 和 DFBT 算法吞吐量方面有较大优势，原因在于本文算法与OVSF-DFSA 算法采用了扩频通信技术，通过对碰撞时隙中的标签全部识别或部分识别，减少了传统算法里面的碰撞时隙数量。相同码长时，本文采用的Logistic 混沌映射方案可提供数量更多的扩频码序列，所以相较于OVSF-DFSA 算法，在同一个碰撞时隙中可以识别更多的标签，从而减少下一帧需要识别的标签数量。本文所提算法吞吐量分别是DFSA、CSP-FSA、DFBT、OVSFDFSA算法吞吐量的61、32、31、2倍。

图6 不同标签数时各算法的吞吐量对比Fig. 6 Comparison of throughput of each algorithm with different number of tags

3 结语

本文针对标签防碰撞算法吞吐量较低问题，提出了基于Logistic 映射的标签可并行识别方案，实现了一个时隙多个标签的并行识别，给出了最优的码长与帧长选取方法，并根据标签识别时反馈给阅读器ID 信息，确立了标签完全识别的判断标准。仿真实验证明，本文Logistic-DFSA 算法用较小帧数和总时隙数有效识别阅读器识别范围内标签，实现了较高的系统吞吐量。但是算法在执行过程中，仍会出现少量无效时隙，下一步算法重点是跳过无效时隙，进一步提高标签识别吞吐量。