基于MRI 图像的阿尔茨海默症患者脑网络特征识别算法

朱 琳，于海涛，雷新宇，刘 静，王若凡

（1. 天津大学电气自动化与信息工程学院，天津300072；2. 唐山市工人医院神经内科，河北唐山063000； 3. 天津职业技术师范大学信息技术工程学院，天津300222）

0 引言

阿尔茨海默症（Alzheimer’s Disease，AD）是目前全世界影响最广的神经系统疾病之一［1］，伴随包括丧失记忆、思考和语言能力等症状，病程缓慢且具有不可逆性，因此AD的早期诊断是神经系统疾病研究的重点。AD往往伴随着大脑神经组织的病变和损伤，以及神经电信号、脑组织异变等现象，如AD患者的脑组织中出现β淀粉样蛋白沉积等生物标志物［2-4］，此类标志物通常可通过脑电图、磁共振成像等神经影像学技术检测［5-8］。对于此类大量的神经影像学资料，诊断过程均需要医生手动标识，耗费大量时间以及劳动力。此外，人工诊断结果存在主观性，往往受限于医生的经验而出现误诊的情况［9-11］。

采用机器学习算法对AD 患者的脑部成像进行分析以及标记可以忽略先验知识的需要，并大大减少诊断所需时间。Trambaiolli 等［12］应用支持向量机（Support Vector Machine，SVM）来识别AD 患者，并采用双极峰的办法识别脑电（ElectroEncephaloGram，EEG）信号的特征。Çevik 等［13］提出了一种基于全自动体素的核磁共振成像（Magnetic Resonance Imaging，MRI）分析算法，可用于AD 早期阶段和轻度认知障碍的辅助诊断。然而基于单一维度的脑部成像往往会忽视大脑不同脑区之间的相互作用，而脑网络可以反映不同脑区电生理活动的特征，并量化其相互耦合的情况，目前广泛应用于大脑成像的研究当中。如Stam 等［14］从AD 患者的脑电图和功能性核磁共振图像静息状态数据中提取出功能网络，发现其小世界特征的丢失。

MRI是一种能够以高分辨率捕获大脑解剖细节的脑成像技术，被广泛应用于AD 临床诊断及研究当中［15-16］。传统的基于MRI 的计算机辅助诊断系统是基于特定目标区域的，这种方法主观性较强，重复性较差［17］。本文将结合计算机分析与功能网络构建，将MRI 图像等分为多个结构块并量化其结构相似性（Structural SIMilarity，SSIM）构建网络，再采用多分类器进行特征识别。

1 数据获取与预处理

本文使用的MRI图像数据来自阿尔茨海默症神经影像学倡议（Alzheimer’s Disease Neuroimaging Initiative，ADNI）数据库，采用了ADNI-1 的标准基准库中的217 个实验对象的1.5 TB MRI 图像。这217 个测试对象包括108 个AD 患者和109个正常人，随机选取其中80个AD患者和80个正常人构成数据集。

实验数据来源之间存在一定个体差异，本次实验中使用的160 位测试对象的MRI图像在位置、脑部形状、脑部大小上存在比较明显的差别，所以需要进行预处理，从而保证后续对各实验对象的MRI图像数据进行分析和比较的有效性。数据预处理过程包括：时间层校正、头动校正以及标准化。

1）时间层校正：为了消除各个扫描层之间采集时间的差异，在保持整段采集信号恒定的前提条件下，通过移动采集信号的正弦相位，前移或后移采集的起始时间进行时间层校正。由傅里叶变换公式

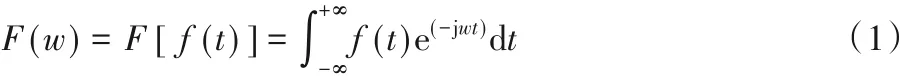
在每个频率的相位中加入一个常值，可实现采集数据起始时间和结束时间的移动。

2）头动校正：为了消除受试者头动位移导致的MRI 扫描异形，把MRI图像序列中各层图像按照第一层对齐，然后根据被试对象的头动数据进行判断，头动若超过一个体素，则弃用该MRI 图像测试例。处理结果发现，AD 组有2 个对象的头动情况超过正常范围，正常组有1 个头动情况超过正常范围，筛选得到78个AD患者和79个正常对照的MRI图像。

3）标准化：将图像配准到MNI152 模板上，通过将不同形状及大小的实验对象的头部置于标准的空间里，实现一个公用的物理坐标系，便于对大脑进行精确的描述。

2 算法设计

2.1 网络构造

本文提出将脑网络特征识别方法应用于MRI图像的分析当中。结构块划分以及脑网络构建的过程如图1 所示。首先将预处理后的全切层MRI 图像依照扫描顺序对齐叠放在一起，可以得到维度为81×96×81 的三维矩阵；进一步将三维矩阵划分为多个结构块，以3×3×3的划分方法为例，结构块之间无重叠则可以划分得到大小为27×32×27 的27 个结构块；接下来将结构块视作网络节点，通过计算任意两个结构块之间的结构相似性构造连接矩阵，进而构建基于MRI的脑网络。

SSIM 是一种直接评估两幅图像之间相似性的方法，通过比较两幅图像之间结构信息的差异造成的图像失真程度，得到客观的评价指标。对图像x和y，x的平均值为μx，方差为σx，y的平均值为μy，方差为σy，σxy为x和y的协方差，则SSIM定义为：

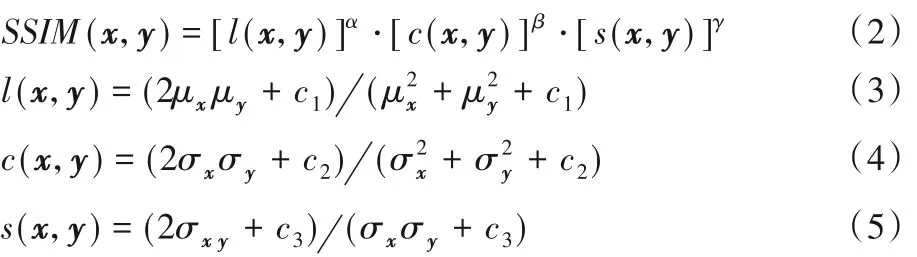
其中：l(x，y)代表亮度比较；c(x，y)代表对比度比较；s(x，y)代表结构比较；c1、c2、c3为常数项，计算中一般设定为α=β=γ= 1，c1=(0.001 ×L)2，c2=(0.003 ×L)2，c3=c32，其中L为像素值的动态范围。SSIM 具有对称性，即SSIM(x，y) =SSIM(y，x)。因此，由定义可知SSIM 的取值范围为［0，1］，其值与相似性成正比，值越大表示两幅图像之间的相似性越高，当两幅图像完全一样时，SSIM值为1。

通过遍历计算任意两个结构块之间的结构相似性指数，可以得到结构相似性矩阵，构建加权网络。设定比例阈值为0.3，对各矩阵保留各自前30%的高相似性值，其余的值置零，可构建得到以结构块为节点的加权复杂网络，并通过二值化得到无权网络。

图1 脑网络构造示意图Fig. 1 Schematic diagram of brain network construction

2.2 网络特征参数提取

图论是分析网络特性的重要研究工具，它通过提取网络的特征参数来量化网络的特性，本文将从基于结构相似性获得的网络中提取加权网络和无权网络的结构参数（全局效率、聚类系数、局部效率、节点介数、边介数）。

假设一个具有N个节点的网络，集合G表示所有节点。定义一个邻接矩阵A来描述节点之间的连接关系，则节点i和j的连接用aij来表示（aij= 1 表示有连接，aij= 0 表示没有连接），边的权值为wij。节点i和j的最短路径长度可以表示为：

其中gi↔j表示节点i到节点j最短的路径。

节点i的全局效率定义为最短路径长度的倒数，即

那么网络的平均全局效率定义为：

单个节点的局部效率定义为：

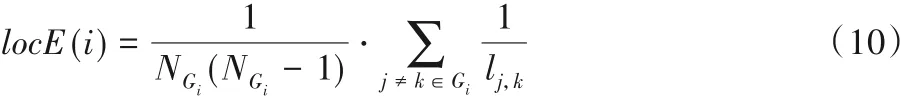
网络的平均局部效率定义为：

聚类系数是评估网络聚集的重要参数，对于无权网络，节点i的聚类系数的计算公式为：

其中：Ki是节点 i 的度，计算公式如式（13）；ti表示节点 i 与它邻接节点j、h可以形成的三角形的数量，计算公式如式（14）。

全局效率以及聚类系数衡量了网络的信息传递能力，也在一定程度上反映了网络的安全性和稳定性。

节点介数定义为网络中所有最短路径中经过该节点的路径的数目占最短路径总数的比例：

边介数定义为网络中所有最短路径中经过该边的路径的数目占最短路径总数的比例：

2.3 机器学习算法

将网络特征参数输入到机器学习模型进行训练，不同的机器学习模型具有不同特点，对不同类型的输入数据适应性存在差异，因此本文中采用多种机器学习算法并对识别结果进行比较，同时对单一特征输入以及多特征组合输入进行比较，采用的算法包括 TSK 模糊分类器［18］、K 近邻（K-Nearest Neighbor，KNN）分 类 器［19］、支 持 向 量 机（Support Vector Machine，SVM）分类器［20］以及朴素贝叶斯（Naïve Bayesian，NB）分类器［21］。TSK 利用多个模糊规则对模型进行表征，具有可解释性高以及泛化性好高等优点；KNN 分类器是一种基于距离计算进行分类的算法，计算效率高；SVM通过构建一个或者多个高维的超平面来对样本数据进行划分，应用普遍且更加直观；NB分类器以贝叶斯定理为基础假设数据样本特征完全独立，是一种基于概率计算的分类器。

3 模型训练及统计分析

将预处理之后的MRI 图像叠放并进行结构块划分，进一步利用SSIM 量化结构块之间的结构相似性，得到连接矩阵，并通过选取阈值构建以结构块为节点的加权网络以及无权网络；再利用图论提取网络的特征并进行统计分析，研究AD 对于网络整体结构特性的影响，并进一步传递给多个分类器进行模型训练以及分类，探讨可能对分类产生影响的参数。

3.1 脑网络结构统计分析

对所有AD 患者和正常对照的结构相似性矩阵的均值进行单因素方差分析组间差异，统计结果显示AD 组为0.253 1±0.088 1，正常对照组为 0.270 3±0.067 5。AD 组的平均值略小于正常对照组，单因素方差分析结果显示p ＞0.1，表示AD和正常对照之间不存在明显的组间差异，因此患病可能没有对MRI整体结构相似性产生明显影响。

进一步应用图论分析法分析脑网络结构特性。利用单因素方差分析分别以全局效率、聚类系数、局部效率、节点介数、边介数作为参数来分析AD 和正常对照之间的组间差异。统计结果如图2（加权）和图3（无权）所示，图中“*”表示p在0.05水平上具有显著性差异（p ＜ 0.05），“△”表示p在0.01 水平上具有显著性差异（p ＜0.01）。对于加权脑网络（图2），AD组的全局效率、聚类系数、局部效率平均值均略微大于正常对照组，以上参数的单因素方差分析结果为p ＞0.05，表示AD和正常对照之间不存在显著差异。AD 组的节点介数大于正常对照组（p ＜ 0.01），边介数相较正常对照组有所减小（p ＜ 0.05），节点介数和边介数均存在显著性差异。对于无权脑网络（图3），AD 组的全局效率、聚类系数平均值均略微大于正常对照组，AD 组边介数较正常对照组略微减小，以上参数的单因素方差分析结果为p ＞0.05，表示全局效率、聚类系数、节点介数在AD和正常对照之间不存在显著差异。AD组的局部效率大于正常对照组（p ＜0.05），节点介数相较正常对照组有所减小（p ＜0.05），局部效率和边介数均存在显著性差异。

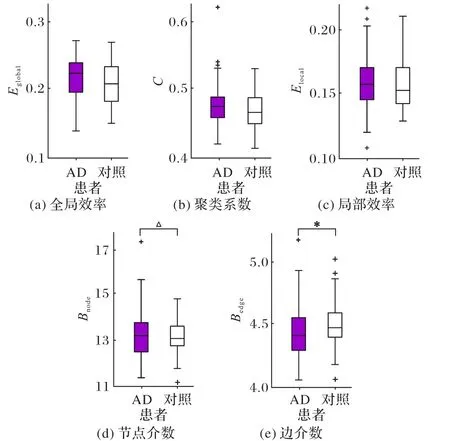
图2 加权网络特征参数统计箱形图Fig. 2 Boxplots of weighted network feature parameters statistics

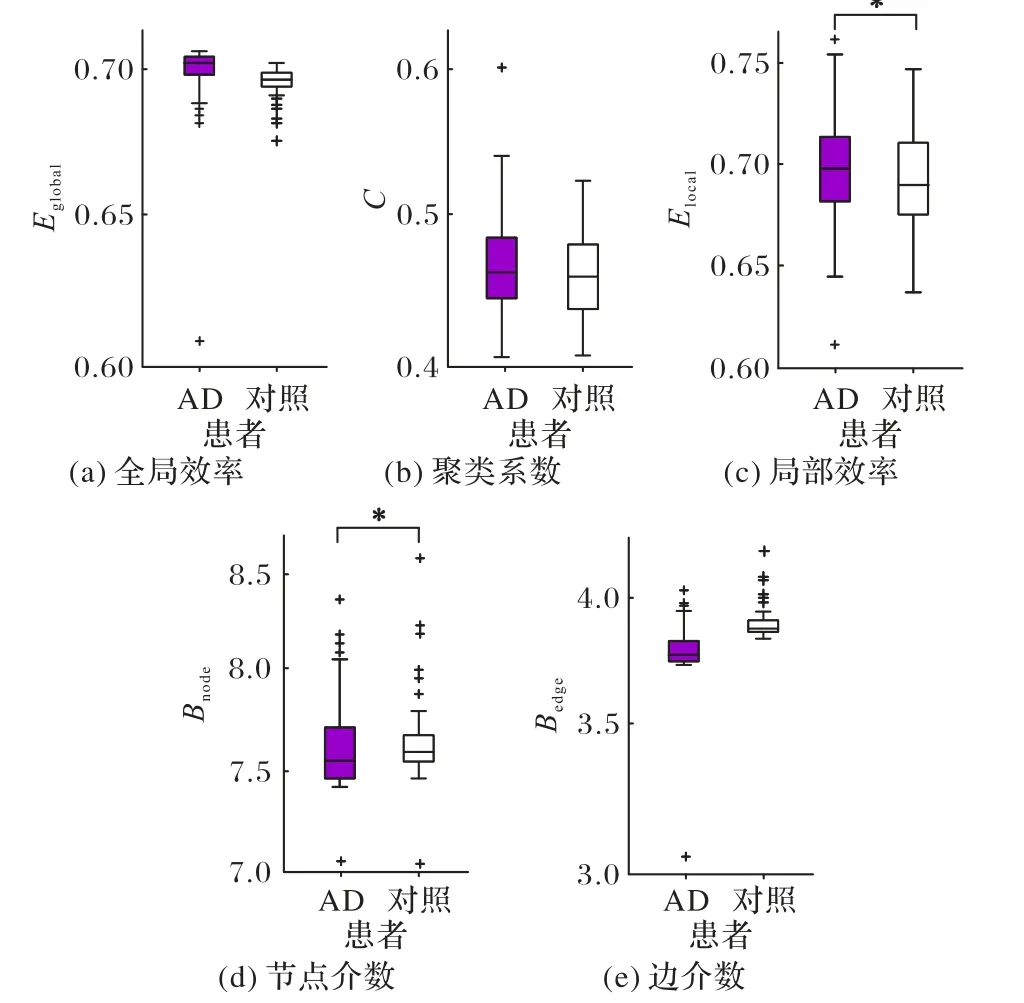
图3 无权网络特征参数统计箱形图Fig. 3 Boxplots of unweighted network feature parameters statistics

3.2 模型训练及机器识别

结构参数的分析结果显示AD 患者脑网络的结构相较对照组存在差异，为了进一步分析这种建网方法的可行性以及比较不同网络特征参数的识别效果，采用机器学习分类器来对脑网络参数进行识别。考虑到不同分类方法对于参数的适应性不同，采用不同的分类方法可能会对识别效果产生影响，因此采用多种通用的分类器分别进行随机抽样来完成脑网络参数的识别以选择更优的分类算法。使用的分类方法包含TSK 模糊分类器、KNN、SVM、NB，分别对AD 的加权脑网络和无权脑网络进行特征识别。由于同时采用多种分类器进行验证，为了避免交叉验证中倍数的选择对不同模型的验证结果可能产生的影响，采用随机抽样验证。训练时首先将数据集划分为训练集和测试集，每次训练将随机提取60 例AD 和60例正常人对照的MRI图像构成训练集，其余的构成测试集；接下来将训练集输入到不同的分类器进行训练学习，并用测试集检验该分类器对AD 脑网络的识别效果。为保证不出现极端测试情况，针对不同的分类器以及输入参数，此过程均将循环500 次并对分类准确率分别取平均。为保证调参的精度，通过网格搜索法对各个分类器参数进行自动优化，最终分类结果如表1所示。

对于加权和无权脑网络，各个分类器均在采用边介数时取得最佳的AD 识别准确率（加粗显示于表1 中）。前文中网络参数的统计分析显示边介数呈现出的差异较大，这种差异同样体现于识别结果中。同样对于加权和无权网络，单一参数识别率最高的分类模型均为SVM 分类器，加权网络的边介数分类准确率为78.42%，无权网络的边介数分类准确率为90.05%。多参数进一步考虑双参数作为输入向量，分类结果如表2所示。

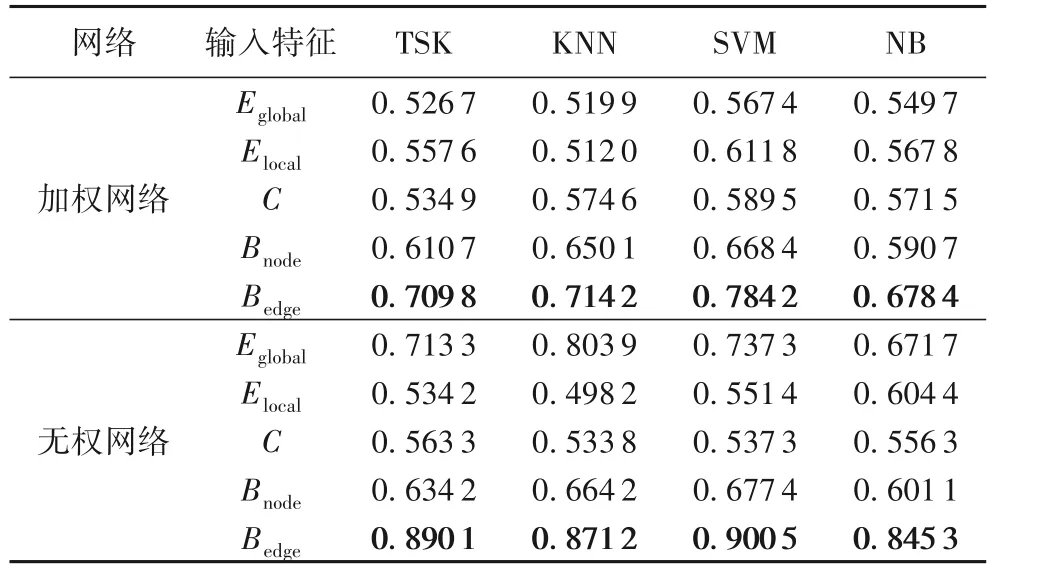
表1 加权网络及无权网络参数单一输入分类结果Tab. 1 Classification results of weighted network and unweighted network with one parameter as single input

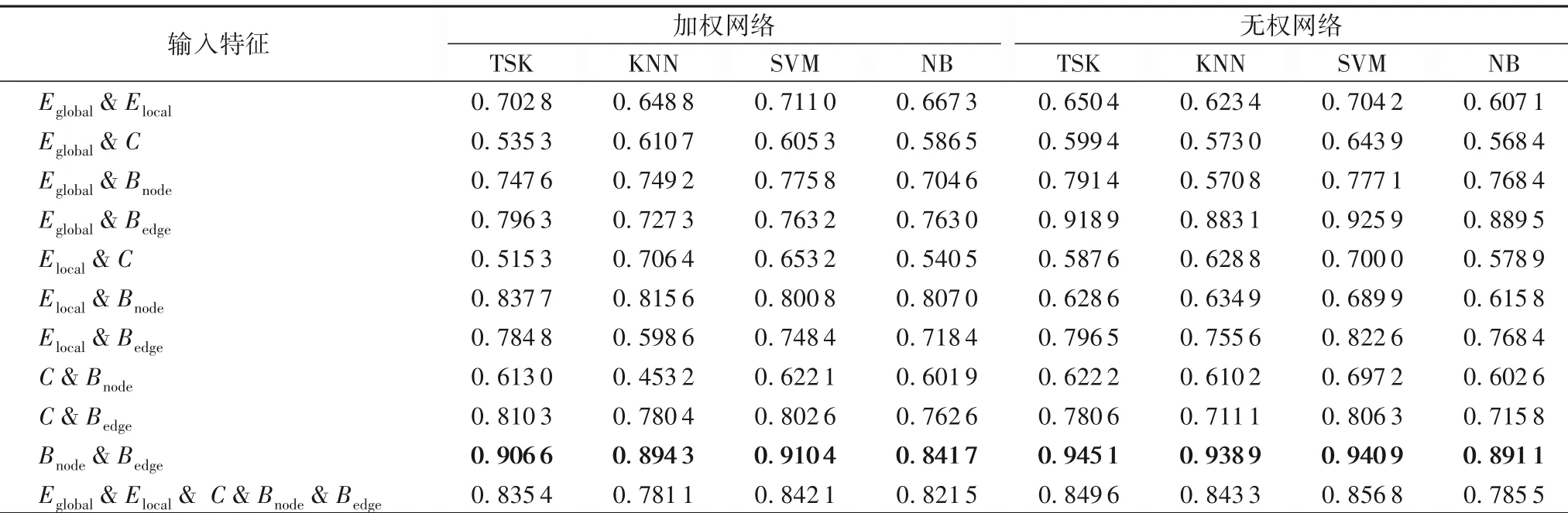
表2 加权网络及无权网络参数多输入分类结果表3 Classification results of weighted network and unweighted network with parameters as multiples inputs

表2 的结果显示多参数作为输入向量时分类效果优于单一输入，对于加权脑网络，各个分类器均在采用节点介数和边介数时取得最佳的AD识别准确率（加粗显示于表2中），TSK、KNN、SVM 和 NB 的最高识别率分别为 90.66%、89.43%、91.04%和84.17%，其中SVM 对AD 识别的准确率最高，NB的识别准确率最低。同样，对于无权脑网络，各个分类器均在采用节点介数和边介数时取得最佳的AD 识别准确率（加粗显示于表2 中），TSK、KNN、SVM 和 NB 的最高识别率分别为94.51%、93.89%、94.09%和89.11%，其中TSK 对AD 识别的准确率最高，NB 的识别准确率最低。此外，各分类器对无权脑网络特征的识别准确率均高于其对加权脑网络的识别准确率。根据多分类器的分类结果，可以得到结论，AD 与正常人脑网络特征中的节点介数和边介数为最有效组合特征。同时对于结构相似性网络，其参数作为双特征输入时模型的分类效果最好，参数输入增加后会产生过拟合降低分类准确性。因此如图4所示，将AD 和正常人脑网络的节点介数和边介数映射到二维平面上。结果表明，对于结构相似性网络以节点介数和边介数为组合时，AD和正常对照之间展现了很高的分离度，同时无权网络的样本分布更为密集，分离度更高。

为了分析结构块化划分方式对网络特性的影响，考虑将全切层（81×96×81）MRI 图像分别划分为16、27、42、54 个结构块，采用SSIM 衡量结构块之间的结构相似性，得到结构相似性矩阵，设定比例阈值0.3，对四种分块方法均保留各自前30%的高相似性值，其余的值置零，分别构建加权网络和无权网络，并计算加权和无权网络的全局效率、聚类系数、局部效率、节点介数、边介数，最后分别采取前文中分类效果最优的分类器以及输入参数对四种结构块划分方法进行脑网络参数识别，对AD的脑网络特征识别结果如图5所示。

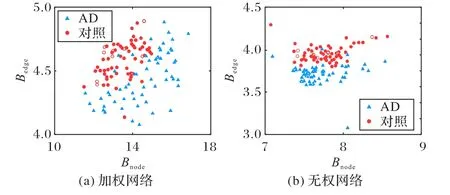
图4 边介数vs. 节点介数分布图Fig. 4 Distribution maps of node betweenness vs. edge betweenness

图5 （a）中统计分析表示在选取16、27、42、54 结构块划分加权网络时，TSK 模糊分类器对单一或特征组合识别的统计，其中圆点为均值，并附有误差带，同理图5（b）为无权网络统计分析结果。由图5 可知，当将MRI 图像划分为27 个结构块时能取得最佳的识别结果，并且随着分块数量增多，TSK 模糊分类器对AD 的识别准确率下降。推测划分的结构块体积过小会导致结构之间相似性降低，结构相似性矩阵中元素值较小且分布集中，所构建的脑网络随机性大，特征识别结果差。

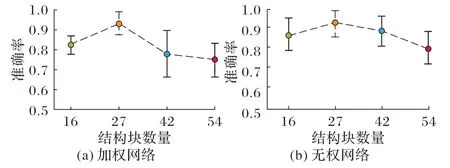
图5 不同划分方法下分类准确率Fig. 5 Classification accuracy of different division methods

4 结语

本文提出了一种基于MRI 图像构建AD 的结构相似性网络的新方法，并提取了脑网络的结构特征参数，结合机器学习算法对AD 进行精准识别。本文方法已实现对AD 样本和健康受试者的识别，且识别正确率高，验证了这种构网方法的有效性。未来希望将所提出的方法进一步应用于AD 的早期诊断上，即包含轻度意识障碍在内的脑网络特征识别，受限于脑电数据采集的有限性，仍需进一步实验验证将脑网络与机器学习方法相结合在识别轻度意识障碍时的有效性，并通过后续实验发现更多的可用于结构相似性网络的特征。