力量训练之最佳功率负荷预测方法构建与评估

梁美富，李 妍，牛雪松

(1.国家体育总局体育科学研究所，北京100061；2.哈尔滨工业大学 体育部，黑龙江 哈尔滨150001；3.沈阳体育学院 社会体育学院，辽宁 沈阳110102)

最大输出功率能力往往是竞技体育赛场上制胜的关键，诸多运动项目技术、战术的充分发挥都架构在骨骼肌的大功率输出能力基础之上[1]，运动员的输出功率能力与竞技专项运动成绩密切相关[2]。

最佳功率负荷指在力量训练过程中某一力量训练手段的输出功率达到最大值时所对应的外界负荷。在该负荷下进行的力量训练即为最佳功率负荷力量训练。最佳功率负荷力量训练能有效刺激骨骼肌产生不同的神经肌肉适应，提高最大功率的输出[3-4]，在兼顾速度和力量的同时，精细化配给力量训练负荷，实现动作输出功率的最大化，提高运动员专项竞技能力所需的投掷能力[5]、跳跃能力[6]、打击能力[3]、变向能力[7]以及加速能力[8]等，满足不同专项运动员力量训练高度专项化和职业化发展的需求。

现代传感技术的不断发展，促使我们能够把握力量训练过程中速度—力曲线关系[9]，也为最佳功率负荷力量训练成功实施奠定了技术基础，最佳功率负荷力量训练诸多的训练效益离不开“剂量负荷”的安排与监控[10]，如何精准确定最佳功率负荷是力量训练实践中的首要因素。通常，确定最佳功率负荷需要进行最大力量测试和输出功率测试，测试最大力量过程往往耗时、耗力，且运动员需要承受一定的运动损伤风险，测试输出功率过程需要借助传感设备得出相应结果进行统计分析，且教练员还需安排适宜的训练负荷来增大测试的精度。此外，对测试过程需精确控制，对采集数据的传感设备的要求，都极大地阻碍了最佳功率负荷力量训练的实践应用。鉴于此，笔者旨在解决确定最佳功率负荷这一实践问题，构建最佳功率负荷的平均速度预测法、非线性回归模型预测法以及BP 神经网络模型预测法，评估3 种预测方法精度，为竞技体育高水平力量训练负荷“剂量化”提供理论与实践支撑。

1 研究对象与方法

1.1 研究对象

北京体育大学体育专业男性大学生52 名，其中，测试对象46 人，预测对象6 人，均有负重半蹲和卧推练习经历。所有受试者均无各种内脏疾病，肝、肾功能正常，无不良嗜好。所有受试者均提前告知参与实验潜在风险，并签署知情同意书。受试者基本情况如表1 所示。

表1 受试者基本情况一览(M±SD)Table 1 Basic information of subjects

1.2 文献资料法

以“力量训练”“功率”“负荷”“Strength Training”“Power”“Optimal Power Load”等为关键词，对CNKI、Wangfang Data、Google Scholar、Web of Science、PubMed 等数据库中相关中英文文献进行混合检索，时间为建库至2020年3月30日，检索到中文类核心期刊论文68 篇，英文类期刊论文2580 篇，纳入8 篇中文、112 篇英文文献重点研读，全面梳理确定最佳功率负荷的方法，为本研究奠定扎实理论基础。

1.3 实验法

1.3.1 实验器材 九轴蓝牙姿态传感器Wit-Motion(BWT901CL)1 个；笔记本电脑1 台；史密斯架2 套(包括标准杠铃杆、杠铃片、固定弹簧夹)；秒表1块；透明胶带1 卷；外置摄像头1 个；备用电源1 块。

1.3.2 实验流程 1)确定测试指标。根据专家建议和相关研究实验设计[11-12]，依据力量训练中动作结构相对简单，技术影响相对较小，爆发式用力为主，使用性最为广泛为原则，确定半蹲起和卧推最大力量作为负荷安排标准，卧推抛和半蹲起为评价指标。2)最大力量测试。采用NSCA 测试方案[13]，对受试者进行卧推和半蹲1RM 测试，作为力量训练负荷的安排依据。3)最大输出功率测试。力量训练负荷为连续型变量，测试密度越大，受试者疲劳感越强，测试准确性就会下降，根据前人研究设计[14-18]和预实验测试情况，确定让受试者在10%、30%、50%、70%和90%1RM 负荷下进行半蹲跳和卧推抛最大输出功率测试，输出功率最大时所应对的负荷即为最佳功率负荷。要求每一级负荷采集1 次试举有效数据，组间间歇时间为2～5 min。

每次测试前，受试者进行15 min 常规热身活动，包括10 min 中等强度慢跑和5 min 动态拉伸，3 min 休息后，进行测试。所有力量测试均在史密斯架上进行，两侧均有保护人员。为减少实验测试误差:1)测试前明确告知受试者实验动作标准并组织练习；2)根据受试者的身高和体重预估其1RM值；3)每次重复动作均给予受试者口头提示与鼓励；4)测试前24 h 内未进行大强度抗阻练习；5)最大力量测试与最大输出功率测试的时间间隔大于48 h。

1.3.3 数据采集 采用MiniIMU(版本号:4.3.14)软件进行数据采集，波特率设置为115 200 bit/s，回传速率为100 Hz，加速度量程为0～8 个重力加速度，计算加速度零偏值，并写入参数，输出内容选择时间和加速度。具体采集流程如下:1)登记运动员的基本信息。2)由实验操作人员在采集软件中进行相关设置，检查设备信号正常。3)设置好测试负荷后，向受试者下达“准备”的口令，受试者上史密斯架后，操作人员进行软件归零设置。4)受试者准备好后，实验操作人员在电脑采集窗口触发采集，发出“3、2、1，开始”指示口令，采样结束后，受试者离开史密斯架，保存数据。5)录制受试者完整运动数据采集过程视频。

1.3.4 数据处理 根据时间、加速度和训练负荷对输出功率、速度和力值计算，具体计算公式如下:Vi＝Vi-1＋ai×ti，Fi＝mi×(ai＋g)，Pi＝Fi×Vi。其中，a为垂直方向加速度，V为瞬时速度，P为输出功率，m为训练负荷，g为重力加速度(10 m/s2)，初速度V0＝0 m/s。

1.4 数理统计法

采用EXCEL 2007 对数据进行汇总计算，将获得的数据导入SPSS 22.0 进行缺失值、异常值和一致性检验，采用单因素方差分析进行显著性检验，采用GraphPad Prism Software 7.0 软件进行图形绘制。所有数据采用均值(M)、标准差(SD)等描述统计量进行表述，其中显著水平为P<0.05，非常显著性水平为P<0.01。

2 研究结果

2.1 平均速度预测法

基于速度的训练(Velocity Based Training，VBT)[19]指在力量训练中依据动作完成的速度指标作为安排负荷标准的训练方法。该方法可以依据动作完成的速度来安排力量训练负荷，预估运动员最大力量[20]以及监控运动员的训练状态[21]等。

本部分研究根据受试者不同专项经历进行统计分析，首先，对受试者进行最大功率输出测试，确定最大功率输出时的各项动力学指标，为下一步分析奠定数据基础；其次，将受试者在最大输出功率时的相关指标进行方差分析，求证哪项指标在各专项间、各力学指标间无显著性差异，进而判断速度预测法是否可行；最后，建立不同负荷下半蹲起和卧推抛的功率-速度曲线关系，确定能预测最佳功率负荷的平均速度值。

卧推抛不同组别各指标数据如表2 所示，最佳功率负荷指标，与投掷组、短跑组、篮球组相比，体操组最小(P<0.01)。最大力量指标，投掷组显著大于短跑组、体操组(P<0.01)。最大力指标，体操组显著小于投掷组、短跑组、篮球组(P<0.01)。平均力指标，体操组显著小于投掷组、短跑组、篮球组(P<0.01)。最大功率指标，体操组显著小于投掷组(P<0.01)。平均功率指标，体操组显著小于投掷组(P<0.01)。仅速度指标各组别间无显著性差异(P>0.05)。

表2 不同组别卧推抛相关指标方差分析结果(M±SD)Table 2 Results of variance analysis of related indexes of bench press throw in different groups

半蹲起不同组别各指标数据如表3 所示，最佳功率负荷指标，投掷组显著高于短跑组、篮球组、体操组(P<0.01)，篮球组、体操组显著高于短跑组(P<0.05)。1RM 指标，投掷组显著大于短跑组、篮球组、体操组(P<0.05)。最大力指标，投掷组、篮球组显著高于短跑组(P<0.05)。平均力指标，投掷组、篮球组显著高于短跑组(P<0.05)。最大功率指标，投掷组、篮球组、体操组显著高于短跑组(P<0.05)。平均功率方面，投掷组、篮球组显著高于短跑组(P<0.01)。仅速度指标各组别间无显著性差异(P>0.05)。

表3 不同组别半蹲起相关指标方差分析结果(M±SD)Table 3 Results of variance analysis of related indexes of half squat in different groups

半蹲起和卧推抛的功率—速度曲线如图1 所示，卧推抛的平均输出功率低于半蹲起平均输出功率，卧推抛平均速度高于半蹲起平均速度。卧推抛最大平均输出功率(549.51 ±193.23)W 对应的平均速度为(1.03 ±0.24)m/s，半蹲起最大平均输出功率(745.28 ±258.64)W 对应的平均速度为(0.86±0.19)m/s。

图1 不同负荷下半蹲起和卧推抛的功率—速度曲线Figure 1 The power-speed curves of the half squat and bench press throw under different loads

2.2 非线性回归模型预测法

回归模型的因变量是自变量的一次以上函数形式，回归规律在图形上表现为形态不尽相同的曲线特征，称为非线性回归[22]。而非线性回归模型是关于未知回归系数具有非线性结构的回归模型，通常反映自变量与因变量之间的非线性数学表达式。

本研究将功率和训练负荷进行标准化，标准化功率为不同负荷下的输出功率除以最大输出功率[23]，标准化训练负荷为相对负荷(训练负荷/最大力量)。采用非线性回归方程对卧推抛和半蹲起进行分析。回归方程具体如下:

其中，Pi代表不同负荷的输出功率，Pmax代表最大输出功率，Li代表不同训练负荷，1RM 代表最大力量，b1、b2、b3代表回归系数，b0代表回归常量。

由图2 可知，卧推抛非线性回归模型的R2为0.421，最大平均输出功率(549.51 ±193.23)W 对应的相对负荷为60.87% ±17.2% 1RM。

图2 卧推抛非线性回归模型Figure 2 Nonlinear regression model of bench press throw

由图3 可知，半蹲起非线性回归模型的R2为0.594，最大平均输出功率(745.28 ±258.64)W 对应的相对负荷为78.26% ±13.71% 1RM。

图3 半蹲起非线性回归模型Figure 3 Nonlinear regression model of half squat

2.3 BP 神经网络模型预测法

BP 神经网络(back propagation network)是一种基于误差反向传播算法训练的多层前馈网络[24]，具有良好的非线性映射能力、任意函数的逼近能力和泛化能力，是应用最广泛的神经网络模型之一。

本研究运用MATLAB2019b 建立BP 神经网络模型，采用三层拓扑结构，将受试者身高、体重、最大力量作为输入层，最佳功率负荷作为输出层。BP 神经网络模型神经元个数根据经验和试错法来确定[25]，通过比较训练集在相同情况下进行训练的网络收敛速度和分类的正确率，最终确定预测模型隐层神经元较为合理的个数为10，隐层神经元个数的经验公式[26]具体如下:

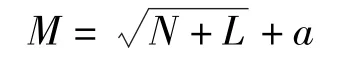
其中，M为隐层神经元个数，N为输入层节点数，L为输出层节点数，a∈(1，10)。

BP 神经网络的输入层到隐含层传递函数通常采用S 型正切函数tansig 作为隐层神经元的激励函数，网络的输出归一化到[-1，1]范围内，预测模型选取S 型对数函数tansig 作为输出层神经元的激励函数，隐含层至输出层的传递函数采用线性函数Pruelin，网络性能函数为mse，网络迭代次数epochs为1 000 次，学习速率lr 为0.05。BP 神经网络模型如图4 所示。

图4 BP 神经网络模型结构Figure 4 BP neural network model structure diagram

将实验测试数据分别作为训练样本输入，随机选择总体样本的70%用于训练集、15%用于验证集、15%用于测试集。采用Levenberg-Marquardt 算法计算并建模。

如图5 和图6 所示，经过2 次的学习后，卧推抛的BP 神经网络预测模型收敛成功，训练集、验证集和测试集的曲线趋势总体一致，该BP 神经网络预测模型训练速度较快，训练效果好。模型拟合曲线的R＝0.777 02，训练集R＝0.722 17，验证集R＝0.887 23，测试集R＝0.860 01，数据点较为均匀分布在拟合曲线附近，该BP 神经网络模型具有较好的训练效果、预测能力和整体拟合效果。

图5 卧推抛最佳功率负荷预测模型训练误差曲线Figure 5 Training error curve of the optimal power load prediction model for bench press throw

如图7 和图8 所示，经过13 次的学习后，半蹲起的BP 神经网络预测模型收敛成功，训练集、验证集和测试集的曲线趋势总体一致，该BP 神经网络预测模型训练速度较快，训练效果好。模型拟合曲线的R＝0.820 93，训练集R＝0.879 92，验证集R＝0.810 67，测试集R＝0.855 61，数据点较为均匀分布在拟合曲线附近，该BP 神经网络模型具有较好的训练效果、预测能力和整体拟合效果。

图6 卧推抛最佳功率负荷预测模型拟合回归Figure 6 Fitting regression of the optimal power load prediction model for bench press throw

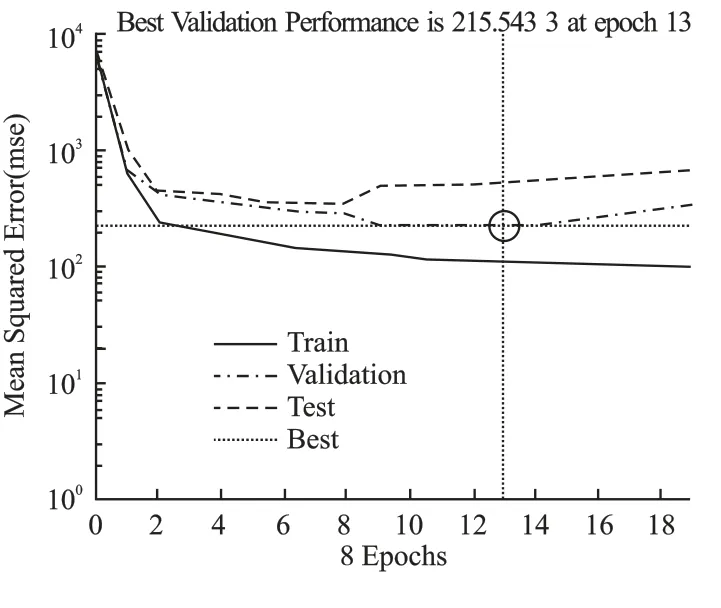
图7 半蹲起最佳功率负荷预测模型训练误差曲线Figure 7 Training error curve of the optimal power load prediction model for half squat

图8 半蹲起最佳功率负荷预测模型拟合回归图Figure 8 Fitting regression of the optimal power load prediction model for half squat

2.4 预测效果对比

运用平均绝对误差和平均相对误差作为对比3种预测方法预测精度的指标。绝对误差即为预测值与实测值的绝对差值；相对误差指的是预测值与实测值的绝对差值占实际值的百分比。绝对误差和相对误差的值越小，表明预测方法的预测精度越高。

2.4.1 卧推抛预测效果对比 绝对误差均值为6名预测对象新样本卧推抛最佳功率负荷的预测值与实测值绝对差的平均值，相对误差均值为6 名预测样本卧推抛最佳功率负荷预测值与实测值的绝对差占实际值的百分比均值，相对误差越低，意味着预测准确率越高，预测精度越高。

如表4 和图9 所示，从6 名预测对象新样本预测结果对比可知，3 种预测方法中BP 神经网络预测误差的绝对值均小于平均速度预测法，且有4 名预测对象预测误差的绝对值小于非线性回归模型预测法，非线性回归模型预测法有6 名预测对象的预测误差的绝对值小于平均速度预测法。BP 神经网络预测法的绝对误差均值和相对误差均值分别为3.79 kg 和9%，小于平均速度预测法的8.50 kg 和25%，小于非线性回归模型预测法的9.33 kg 和31%。总体而言，BP 神经网络预测法对预测样本的最佳功率负荷预测最精确，其次为平均速度预测法，最后为非线性回归模型预测法。

2.4.2 半蹲起预测效果对比 如表5 和图10 所示，从6 名预测对象新样本预测结果对比可知，3 种预测方法中，BP 神经网络的预测误差的绝对值均小于平均速度预测法和非线性回归模型预测法；平均速度预测法有4 名预测对象的预测误差的绝对值小于非线性回归模型预测法。从绝对误差均值和相对误差均值来看，BP 神经网络预测法的绝对误差均值和相对误差均值分别为6.91 kg 和9%，小于平均速度预测法的10.05 kg 和13%，小于非线性回归模型预测法的14.60 kg 和20%。总体而言，BP 神经网络预测法对预测样本的最佳功率负荷预测最精确，其次为平均速度预测法，最后为非线性回归模型预测法。

表4 卧推抛最佳功率负荷预测精度对比Table 4 Comparison of prediction accuracy of optimal power load in bench press throw

图9 卧推抛最佳功率负荷预测结果Figure 9 Prediction results of the optimal power load of bench press throw

图10 半蹲起最佳功率负荷预测结果Figure 10 Prediction results of the optimal power load of half squat

表5 半蹲起最佳功率负荷预测精度对比Table 5 Comparison of prediction accuracy of optimal power load in half squat

3 讨论

就3 种预测方法的精度而言，半蹲起力量训练的最佳功率负荷预测精确性方面，BP 神经网络的预测结果准确性和稳定性最高，其次是平均速度预测法，最后是非线性回归模型预测法。卧推抛力量训练的最佳功率负荷预测精确性方面，BP 神经网络的预测结果准确性和稳定性最高，其次是非线性回归模型预测法，最后是平均速度预测法。BP 神经网络是通过网络的自学习能力，建立预测变量到被预测变量的多维函数非线性映射，从而获得一个预测效果比较好的预测模型，其预测效果最佳，且随着测试样本数据的不断丰富，其预测效果亦会得到显著提升。平均速度预测法在对不同力量训练手段的最佳功率负荷预测时，依据力量训练过程中的平均速度指标，由于平均速度具有较小的变化范围，因此能够较为敏感地反映出运动员的训练状态。本研究结果显示，平均速度预测法的预测精度不如BP 神经网络预测法，一方面可能是由于BP 神经网络预测法更加精确；另一方面是由于在实际测得不同力量训练手段的最佳功率负荷时，为兼顾运动员疲劳与测试的准确性，测试的负荷区间划分相对较大，平均速度预测法测试结果仅能与其固定负荷进行对比，可能造成一定的系统误差，平均速度预测法在实践应用时亦有可能具有更好的预测效力，但仍需后续研究进行深入研究。非线性回归模型预测法是依据受试者不同力量训练手段的最大力量来预测最佳功率负荷，从6 名测试对象预测结果来看，非线性回归模型预测法的相对误差值大于其他两种预测方法，其中预测半蹲起最佳功率负荷的误差值大于卧推抛最佳功率负荷的误差值。这一现象主要由以下因素造成:1)参与半蹲起抗阻力量训练手段的肌群大于卧推抛抗阻力量训练的肌群，半蹲起能对抗更大的外界负荷，表现出更大的最大力量，相应的误差值也会增大，即对抗外界阻力越大的力量训练手段，其相对误差值也会有所增大，对抗外界阻力越小的力量训练手段，其相对误差值也会有所减小；2)不同运动员的同一力量训练手段也会表现出不同的最大力量水平，通常，非线性回归模型预测法最大力量越大，相应的误差值也会增大；最大力量越小，其相应的误差也会减小。

就3 种预测方法的实践应用而言，测试指标数量方面，BP 神经网络预测法需要测试3 项指标，而非线性回归模型预测法和平均速度预测法仅需测试1 项指标。各指标获取的难易程度方面，BP 神经网络预测法和非线性回归模型预测法的指标获取相对容易，对测试设备的要求相对较低，平均速度预测法需要更精确和稳定的速度采集设备来确定不同力量训练手段的最佳功率负荷，对设备的要求相对较高。应用不同预测方法的安全性方面，BP 神经网络预测法和非线性回归模型预测法需要测试不同力量训练手段的最大力量，具有一定的运动损伤风险，而平均速度测试法依据力量训练动作过程中的平均动作速度来进行最佳功率负荷力量训练，无需测试最大力量，能在一定程度上降低运动损伤发生风险。3 种预测方法应用的便捷程度方面，平均速度预测法具有省时省力、可信度、安全性以及可行性高等特点，测试力量训练动作完成的平均速度，仅需一个稳定的数据采集设备，操作相对简单，方便携带和采集数据，易于教练员安排特异性的力量训练；其次是非线性回归模型预测法，对数据采集设备要求最低，但需采集不同力量训练手段的最大力量，测试过程相对费时费力，且有一定的运动损伤风险，整个测试过程易于教练员操作与掌控；最后是BP 神经网络预测法，亦需要面临相对费时费力的最大力量测试过程，此外，还需要测试运动员的身高和体重信息，采用相关的软件和程序，在已训练好的BP 神经网络模型上进行不同力量训练手段最佳功率负荷结果的预测，BP 神经网络预测法的程序和步骤相对较多，教练员实际操作和应用的难度相对较高。

就3 种预测方法的应用前景而言，BP 神经网络的智能化程度最高，训练好的BP 神经网络模型具有任意复杂的模式分类能力、多维函数非线性映射能力、柔性的网络结构、自学习能力以及自适应能力，能够较为准确地预测不同力量训练手段的最佳功率负荷，随着力量训练数据的不断丰富和积累，通过BP 神经网络对力量训练的大数据进行自我学习，可以不断提高最佳功率负荷的预测精度；另外，随着力量训练数据的不断丰富，亦可以根据测试对象性别和运动水平等信息等进行多维度精细化划分，实现对不同人群不同训练水平者最佳功率负荷的精确预测。而平均速度预测法和非线性回归模型预测法仅是对个体数据的采集、分析和应用，随着后期力量训练数据的积累，也可以通过划分不同的性别和力量训练水平等因素进行重新调整平均速度预测法和非线性回归模型预测法的参数，以求取得更好的预测效果，但其缺乏自我学习的能力、自动处理大数据的能力以及多维度映射的能力。

综上，通过6 名预测对象的实例预测验证以及3 种最佳功率负荷预测方法优缺点的对比分析可知，3 种不同力量训练手段最佳功率负荷的预测方法中，BP 神经网络预测法具有最高的预测精度和广阔应用前景，但其实际操作和应用的难度亦相对较大。平均速度预测法相对省时省力，具有较强的预测精度，能规避测试最大力量的运动损伤风险，具有最强的实用性，但其对速度采集设备的精确性和稳定性要求较高。非线性回归模型预测法对训练设备的要求相对较低，整个测试过程易于教练员操作与掌控，但其预测误差相对较大，更适合于用于训练水平较低，或是力量水平较低者不同力量训练手段最佳功率负荷的预测。教练员可根据3 种最佳功率负荷预测方法的优缺点、运动员的力量训练水平以及力量训练设备实际情况选择最适宜的最佳功率负荷预测方法。但值得注意的是，以上3 种不同力量训练手段最佳功率负荷的预测方法仅为不同力量训练手段最佳功率负荷的确定提供一个训练负荷参考和研究视角，其中平均速度预测法、非线性回归模型预测法以及BP 神经网络预测法3 种预测方法均有其优点和局限，教练员在应用3 种预测方法来确定不同力量训练手段最佳功率负荷时，应充分考虑了解3 种预测方法的优缺点，在确定不同力量训练手段最佳功率负荷的基础上，结合运动员的力量训练实际情况进行灵活运用，切莫教条主义。

本研究在严格实验设计和控制实验流程的基础上，仍存在以下局限性:1)受试者的选取上，由于实验条件局限性，未涉及女性受试者以及多个运动水平受试者，最佳功率负荷在不同人群训练实践应用时，仍需进一步精确测量。2)力量训练负荷的切割上，考虑受试者疲劳问题，连续型变量负荷的切割仍具有较大变异范围，未来可进一步精细化力量训练负荷。3)负重器材的选择上，考虑受试者安全问题，仅在史密斯架上进行实验，可能导致最佳功率负荷大于自由重量器材所得数值。

4 结论与建议

本研究建立了3 种最佳功率负荷的快速预测方法，包括平均速度预测法、非线性回归模型预测法和BP 神经网络预测法。其中，BP 神经网络预测法预测精度和智能化程度最高，但其实际操作和应用的难度亦相对较大；平均速度预测法运用的便捷性最优，但其对设备的要求相对较高；非线性回归模型预测法对设备要求最低，但其预测误差相对较大，更适合训练水平相对较低的运动员。

建议不同力量训练最佳功率负荷快速预测方法应用时，应重点注意其试用条件应是在史密斯架上，并按照相同标准动作全力完成每次试举。当应用自由重量器材进行最佳功率负荷力量训练时，可将所得最佳功率负荷预测值进行适当调整，切莫刻舟求剑。