压电柔性结构形状复合控制方法研究

张宗宇，周文雅，吕维梁，王晓明，马瑞鑫

(1.大连理工大学 航空航天学院,辽宁 大连 116024；2.中山大学 航空航天学院,广东 广州 510006)

0 引言

随着科学技术的发展，压电驱动柔性结构被广泛用于柔性机翼主动变形、太阳能帆板、大型空间反射器结构型面调整及发动机、机翼颤振的主动抑制等航空航天领域。与其他压电形式驱动源相比，压电纤维材料驱动器因其能量密度大，控制带宽高，环境适应性好及体积小等优势而受到研究者的广泛青睐[1-6]。但压电纤维材料固有的迟滞、蠕变特性严重影响其控制精度，给结构高精度形状控制带来严重挑战。

目前，许多学者已针对压电材料的迟滞蠕变特性进行了理论研究和压电驱动结构变形控制的研究[7]。赵天等[8]提出了一种基于迟滞蠕变前馈补偿控制与自适应滤波反馈控制相结合的前馈-反馈复合控制法，并成功应用于压电陶瓷层叠作动器控制中；Shrock等[9]对宏纤维复合材料(MFC)的迟滞蠕变特性进行了逆补偿研究及基于前馈补偿的MFC驱动柔性结构形状控制实验；周淼磊等[10]构建了BP神经网络迟滞蠕变模型，与专家模糊控制相结合，有效提高了压电陶瓷驱动平台定位精度；赵庆旭等[11]采用二阶多项式模型构建了压电陶瓷作动器迟滞模型，开展了压电陶瓷定位平台复合控制方法的研究。为解决现有压电驱动结构形状控制研究中存在的被控对象和压电作动器迟滞蠕变建模方法粗糙、精确度低、通用性及可扩展性差等问题，进一步探讨提高控制精度的有效方法。本文开展了MFC驱动柔性结构高保真动力学建模和前馈-反馈相结合的动态形状复合控制方法研究。首先，采用有限元法、均匀化理论结合压电驱动载荷比拟法，建立了压电驱动柔性结构力-电耦合动力学模型，采用模态降阶法推导了其状态空间形式控制模型。进一步构建了基于实验数据的Prandtl-Ishlinskii(PI)迟滞模型和lg(t)形式蠕变模型，推导得到其逆模型，并据此开展前馈补偿控制器设计。在前馈补偿的基础上，结合线性自抗扰反馈控制法，实现了压电驱动柔性结构的前馈-反馈混合控制器设计，并通过仿真算例验证了本文所提控制方法的可行性及其在控制精度方面所具有的优势。

1 数学模型

1.1 压电驱动柔性结构动力学模型

图1为MFC驱动柔性悬臂铝板实验结构。M8528P1型MFC压电纤维作动器粘贴在被控结构根部。利用压电材料的逆压电效应，可将电压激励转化为自身结构应变，实现对被控结构形状的控制,控制原理如图2所示。研究过程中采用被控结构端部测量点挠度来定量刻画结构变形量。

图1 MFC驱动悬臂铝板结构示意图

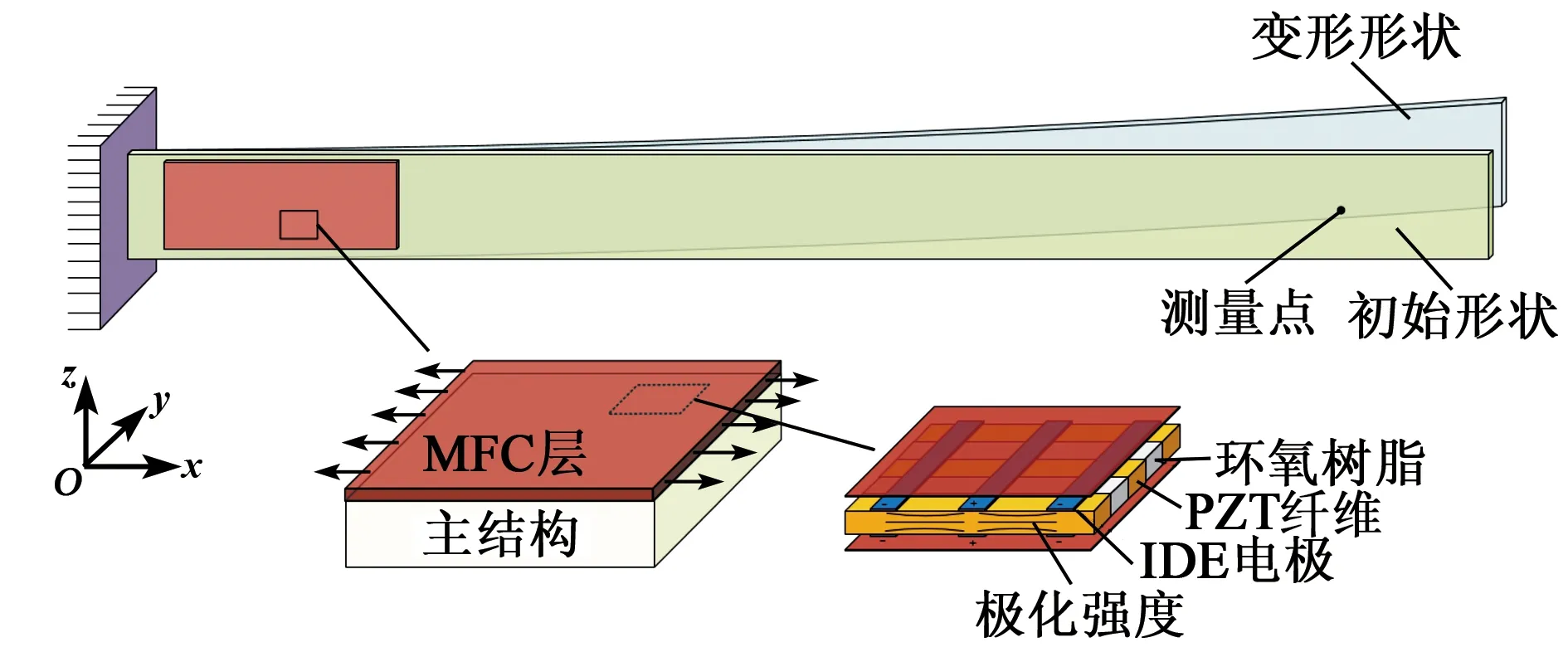
图2 形状控制系统示意图

研究中采用四节点板单元结合有限元法建立了压电驱动柔性结构动力学模型[12]。建模过程中利用压电驱动载荷比拟法[13]实现输入电压-输出力(矩)的转换。模型中包含被动单元和主动单元(粘贴有压电纤维作动器的单元)[14]。

将被动单元和主动单元进行组装，得到压电驱动柔性结构整体控制方程为

(1)

式中：xs为结构位移矢量；Ms=Msb+Msp和Ks=Ksb+Ksp分别为整体质量矩阵和刚度矩阵，下标b和p分别对应于悬臂板结构和压电驱动器的相关变量；Fp为单位电压下产生的压电控制力(矩)矢量;u为作动器施加的电压矢量。表1为被控结构及驱动器属性。

表1 被控结构及驱动器属性

由于所建结构动力学模型阶数较大，为便于开展控制率设计，采用模态分解法对所建立的有限元模型开展降阶工作，引入模态坐标变换[14]：

xs=Φq

(2)

式中：q为广义坐标向量；Φ为系统振型矩阵。

为模拟结构在电压激励下的真实变形响应，还须考虑结构阻尼效应。本文采用经典阻尼模型，其数值通过实验数据获得。进一步考虑结构阻尼，降阶后的结构动力学模型为

(3)

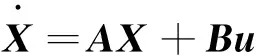
(4)

式中A,B分别为系统矩阵和输入矩阵。

研究中，被控结构的变形量用测点的弯曲挠度来表示，则有

y=CyX

(5)

式中：y为输出变量；Cy为输出矩阵。

1.2 MFC作动器迟滞蠕变建模及其逆补偿

研究中采用的MFC具有压电材料所固有的迟滞与蠕变特性。迟滞特性表现为在升压或降压的过程中，作动器对应的输出位移表现出明显的回路特征[15](见图3(a))；蠕变特性表现为作动器在如图3(b)所示稳定加载电压下，其驱动位移呈现出如图3(c)所示的随时间发生漂移的特性。为提高压电作动器的驱动精度，本文对压电纤维作动器的迟滞蠕变特性进行了精细化建模，并对其逆补偿法进行了重点研究。

图3 MFC驱动器迟滞蠕变特性

1) 迟滞建模。研究采用PI迟滞模型描述MFC的迟滞特性。PI迟滞模型属于唯象模型，可通过实验数据来刻画迟滞非线性效应。PI迟滞模型H[x](t)由nH+1个基本单元迟滞算子线性加权叠加得到：

(6)

式中：wHi为权系数；rHi为阈值；zH0i(i=0,1,…,nH)为初值。

基本单元迟滞算子定义为在分段单调时间区间内t0≪…≪tj≪t≪tj+1≪…≪tend输入信号的递推关系[8]，具体形式为

zH(t)=max{x(t)-rH,min{x(t)+

rH,zH(tj)}}

(7)

其中初值为

zH(t0)=max{x(t0)-rH,min{x(t0)+

rH,zH(t0)}}

(8)

2) 蠕变建模。MFC的蠕变特性表现为在稳定驱动电压作用下，压电系统输出位移随时间改变的一种滞后效应。由于其位移特性与时间呈现对数变化关系，可由lg(t)型蠕变算子进行描述，其由m个基本单元蠕变算子叠加得到：

(9)

式中:m为蠕变特征值个数;rK∈R+为阈值。

基本单元蠕变算子，即

zK(t)=KrKaK0[x,zK0]

(10)

式中zK0为初值。

式(10)为下式所示非线性微分方程的唯一解，即

rK,min{x(t)-zK(t)+rK,0}}

(11)

式中aK∈R+为蠕变特征值,其具体值如下：

(12)

式中Ts为时间序列的最小间隔。

PI形式蠕变算子由nH+1个阈值为rKi的lg(t)蠕变算子加权叠加得到：

(13)

式中wKi为权系数。

将蠕变算子与迟滞算子相结合，可得非线性迟滞蠕变模型：

(14)

结合实验数据，通过系统辨识法可得迟滞蠕变模型算子的参数。利用这种基于算子的模型，方便计算其逆算子，并建立逆模型来补偿迟滞蠕变效应。补偿模型为

x(t)=G-1[y](t)=H-1[y-K[x]](t)

(15)

由于本文研究重点是压电驱动柔性结构形状的复合控制，故针对MFC迟滞和蠕变模型参数辨识法及其逆模型推导过程不再给出，详细信息可参考文献[16-17]。

2 柔性结构非线性模型及控制器设计

2.1 MFC驱动柔性结构非线性控制模型的建立

通过有限元法、均匀化理论和载荷比拟法，结合模型降阶手段得到MFC驱动柔性结构状态空间形式控制模型。该模型不包含MFC作动器的非线性特性。因此，基于1.2节建立的MFC作动器迟滞蠕变模型获得被控系统非线性特征，将其与建立的压电驱动柔性结构线性模型串联，最终可得到包含压电驱动器迟滞、蠕变特性的被控系统非线性模型，如图4所示。

图4 压电驱动柔性结构非线性控制模型

2.2 压电驱动柔性结构前馈控制器的设计

完成压电驱动柔性结构高保真形状控制建模后，基于迟滞蠕变逆模型实现了面向被控系统的前馈补偿控制器设计(见图5)，并对被控结构进行动态变形的开环全补偿控制实验。前馈补偿实验流程如下：

1) 依据被控系统线性模型求解跟踪预定变形轨迹的所需电压。

2) 将得到的电压加载轨迹作为前馈逆补偿控制器输入，经迟滞蠕变逆补偿后得到实际控制电压加载曲线。

3) 将补偿后的电压作为实验系统输入，进行被控对象结构形状控制。

图5 开环前馈补偿控制示意图

在研究过程中，为避免大柔性结构形状变化过程中的振荡效应对迟滞蠕变建模精度产生影响，使用较短铝板来研究MFC的迟滞蠕变非线性特征。图6为该短铝板的实物图及对应的有限元模型。

图6 迟滞蠕变逆补偿研究用压电驱动层合铝板结构

图7(a)为通过MFC驱动短铝板开环变形实验测量的电压-位移数据滞回曲线。图7(b)为经过迟滞蠕变逆模型补偿后得到的一组电压-位移响应关系曲线。对比图7(a)、(b)可知，经逆补偿后，可得加载电压-驱动位移间呈近似线性关系，由此表明迟滞、蠕变非线性得到了很好的补偿。后续研究中，将基于该实验数据开展柔性结构迟滞、蠕变前馈补偿器设计工作。

图7 迟滞蠕变非线性关系补偿

对实验系统分别施加如图8(a)所示的加载电压(对应测量点终端稳态位移量为5 mm)，可得到如图8(b)所示的位移响应曲线。由图8(b)可知，压电作动器的迟滞蠕变作用对实验系统控制精度影响严重。建立的前馈补偿器能够有效消除迟滞、蠕变效应对结构控制精度带来的影响。对比仿真与实验数据可知，建立的被控对象模型具有较高精度，且能良好地模拟被控对象结构动力学特性。

图8 开环补偿控制结果示意图

2.3 压电驱动柔性结构复合控制系统的设计

为提高控制系统增益，改善系统控制精度及提升系统鲁棒性，本文采用自抗扰法设计面向形状控制的闭环反馈控制器，并与基于迟滞蠕变模型的前馈控制器相结合，构建了面向压电驱动柔性结构形状的复合控制系统。图9为构建的复合控制系统示意图。自抗扰控制器主要由微分跟踪器(TD)、状态反馈环节(LF)和状态扩张观测器(LESO)3部分组成[18]。

图9 压电驱动柔性结构形状复合控制示意图

针对本文涉及的典型二阶受控系统，设计自抗扰控制率为

U0=Kp(r-Z1)-KdZ2

(16)

(17)

式中：U0为由状态误差反馈控制率解算得到的控制输入;U1为由自抗扰控制器解算得到的控制输入；Z1、Z2、Z3为三阶状态扩张观测器的观测输出；r为系统控制指令输入；Kp，Kd为控制参数；b0为由被控对象特性和参数决定的常量参数。

将U1与经过迟滞、蠕变前馈补偿得到的前馈输入Uq进行求和，得到所设计的复合控制器整体输入U为

U=U1+Uq

(18)

3 仿真研究

为检验复合控制法对结构动态形状控制的效果，在MATLAB/Simulink环境下构建了压电驱动柔性结构形状闭环控制仿真平台，并开展了数值仿真研究。本文在线性自抗扰控制(LADRC)系统中，状态扩张观测器的参数选取β1=150，β2=120，β3=125×103，反馈参数Kp=1 000，Kd=8，b0=0.01。为对比显示LADRC控制法在控制精度和鲁棒性上的优势，还搭建了基于比例、积分、微分(PID)控制与迟滞、蠕变前馈补偿相结合的复合控制系统。通过自调节整定PID参数Kp=5×104，Ki=7×102，Kd=5×104。

在研究中采用正弦形式的控制信号yr=0.005sin(0.125πt)作为期望输入，对被控对象分为下述3种情况进行仿真：

1) 在无外界干扰条件下，单独采用LADRC控制法和PID法对实验系统进行动态变形控制。图10为两种控制方法的控制效果和控制误差。

图10 控制效果展示

2) 在无外界干扰条件下，将LADRC控制法和PID控制法分别与迟滞、蠕变前馈逆补偿控制相结合，对实验系统进行动态变形控制。图11为两种控制方法的控制效果和控制误差。

图11 控制效果展示

3) 将LADRC控制法和PID控制法分别与迟滞、蠕变前馈逆补偿控制相结合，对实验平台进行动态变形控制。采用正弦信号y=50sin(0.5πt)作为输入干扰信号施加于仿真过程中，图12为两种控制方法的控制效果和控制误差。

图12 控制效果展示

图13为分别采用LADRC和PID结合迟滞、蠕变前馈补偿控制的复合控制法及单独采用LADRC和PID反馈控制法的误差曲线。基于仿真结果，计算得到4种控制方法下的控制位移与期望位移的平均绝对误差分别为0.038 6 mm、0.108 1 mm、0.484 5mm、1.537 3 mm。

图13 控制误差对比图

对比图11和图12的仿真结果可知，MFC迟滞、蠕变特性对系统控制精度影响严重，在LADRC和PID闭环控制下，引入迟滞蠕变前馈补偿控制器后，系统控制精度分别提高了2.8倍和3.2倍。

由图13可知，LADRC复合控制法除能够提高被控对象的控制精度外，闭环系统的抗干扰能力和鲁棒性也得到增强。在引入干扰信号后，LADRC复合控制法的控制能力几乎无变化，而PID复合控制法则难以实现对控制输入的有效跟踪。由此可知，LADRC控制法对这种压电驱动大柔性结构动态形状的控制更具优势。

4 结论

1) 本文进行了压电驱动柔性结构形状复合控制的理论研究。基于有限元法、均匀化理论和载荷比拟法，构建了面向MFC驱动柔性结构形状的控制模型。对比实验数据，所建立的控制模型具有良好的精度。建模方法对于指导压电材料驱动大柔性结构形状控制具有实际参考价值。

2) MFC作动器迟滞蠕变特性对结构动态形状控制精度影响严重。建立了基于实验数据PI迟滞模型与lg(t)形式的蠕变模型，开展了迟滞蠕变前馈逆补偿控制器设计。实验结果表明，所设计的前馈控制器能有效消除MFC的非线性，满足高精度形状控制的工程需要。

3) 构建了基于迟滞、蠕变非线性逆补偿模型的前馈控制和自抗扰反馈控制相结合的复合控制系统。仿真算例表明,复合控制法能在保证系统稳定性前提下实现对结构形状的有效控制，前馈补偿控制能够提高控制精度。同时仿真结果表明，与经典PID控制法相比，LADRC具有更高的抗扰性和鲁棒性。