基于相位负反馈的振弦式陀螺驱动电路研究

陈志龙，黄 鸣，刘 鹏，舒 凯

(1.南昌理工学院 电子与信息学院，江西 南昌 330044；2.华东交通大学 机电与车辆工程学院，江西 南昌 330013)

0 引言

陀螺是一种测量物体角速度的惯性传感器[1]，广泛应用于海、陆、空、民等多个领域。传统机械陀螺和光学陀螺精度高，但由于受其体积和成本的影响，一般应用于航天航空、导弹制导、深海探测等高科技领域[2]，微机械陀螺体积小但精度不高，一般应用于机器人、汽车电子、消费电子等对精度要求不高的民用领域[3]。为了提高陀螺的精度并降低成本，陀螺的高精度化和小型化成为现代陀螺的研究重点。传统基于哥氏效应的微机械陀螺大都采用幅值检测方式，很难兼顾陀螺的小型化与高精度化。振弦式陀螺采用频率检测方式，陀螺体积越小，检测模态固有频率越高，则陀螺检测精度越高，抗干扰能力也越强。由于振弦式陀螺检测模态的频率信号中会调制加速度信号和驱动模态振动信号，故产生稳定可靠的驱动信号对解调出加速度信号至关重要[4-5]。

目前产生交流驱动信号的方法主要有两种：

1) 自激驱动方式[6-7]。将驱动模态的振动信号经滤波放大处理后直接作为陀螺的驱动信号，这种方式产生的驱动信号存在寄生相位误差，驱动系统的建立时间长，驱动频率误差大。

2) 锁相环驱动方式[8-9]。利用输入信号与压控振荡器(VCO)输出信号的相位差信号，控制VCO的振荡频率追踪输入信号的频率，这种方式调节范围小，超出锁定范围则会导致频率失锁。

本文对振弦式陀螺驱动模态进行了理论分析，针对传统自激驱动方式和锁相环驱动方式的不足，设计了一种用于振弦式陀螺的相位负反馈驱动电路，以满足驱动信号自动调节与快速稳定的目的，并通过仿真分析和驱动测试验证了该闭环驱动电路的可行性。

1 振弦式陀螺闭环驱动理论分析

1.1 振弦式陀螺工作原理

振弦式陀螺结构如图1所示，将陀螺置于向上的均匀磁场中，外框架内的驱动框架和弹簧构成陀螺的驱动模态，驱动框架内的质量块、振弦和支撑梁构成陀螺的检测模态。驱动框架在通电导线的作用下带动质量块沿y方向简谐振动，当陀螺在z方向以角速度Ω转动时，质量块会受到x方向的哥氏力传递给振弦，使质量块两边振弦的固有频率f1与f2发生改变，通过解调f1、f2的变化即可求出Ω的变化。

图1 振弦式陀螺结构原理图

振弦式陀螺采用电磁驱动方式[10]，对陀螺驱动框架的外圈布置的驱动导线两端施加交变电压，通电导线在磁场的作用下产生安培力带动驱动框架振动。

驱动导线受到的安培力公式为

(1)

式中：Vd为施加在驱动导线上交变电压的幅值;ωq为交变电压的频率;R为驱动导线的电阻;B为磁场的磁感应强度;L为有效切割磁感线的导线长度。

陀螺驱动后，驱动框架带动质量块在驱动方向做简谐振动。

设驱动框架的振动位移为

x=Asin(ωt)

(2)

式中:A为驱动框架的振幅；ω为驱动框架的振动频率。振弦方向产生的哥氏力(Fc)与Ω的关系式为

(3)

式中m为质量块的质量。Fc与f1、f2的关系式分别为

(4)

(5)

式中:l为振弦长度;F0为振弦预紧力;ρ为振弦线密度。将式(3)分别代入式(4)、(5)后进行差分求解，可得Ω与f1、f2的关系式为

(6)

由式(6)可看出，Ω与驱动模态的振动信号有关，当陀螺以其固有频率稳幅振动时，通过分别测量同一时刻的f1和f2，即可求解出Ω[11]。

1.2 陀螺驱动理论分析

振弦式陀螺驱动方向的运动可等效为质量弹簧阻尼系统(见图2)。

图2 振弦式陀螺等效动力学模型

图2所示驱动模态动力学模型方程为

(7)

式中：my为驱动框架和中心质量块的质量和;ky为质量弹簧阻尼系统的弹性系数;cy为质量弹簧阻尼系统的阻尼系数;Fy为交变安培力的幅值;ωa为交变安培力的频率。对式(7)求解，只考虑稳态项，得

x=Asin(ωt+φy)

(8)

(9)

(10)

根据式(9)、(10)可绘制出陀螺驱动模态的频率特性曲线，如图3所示。

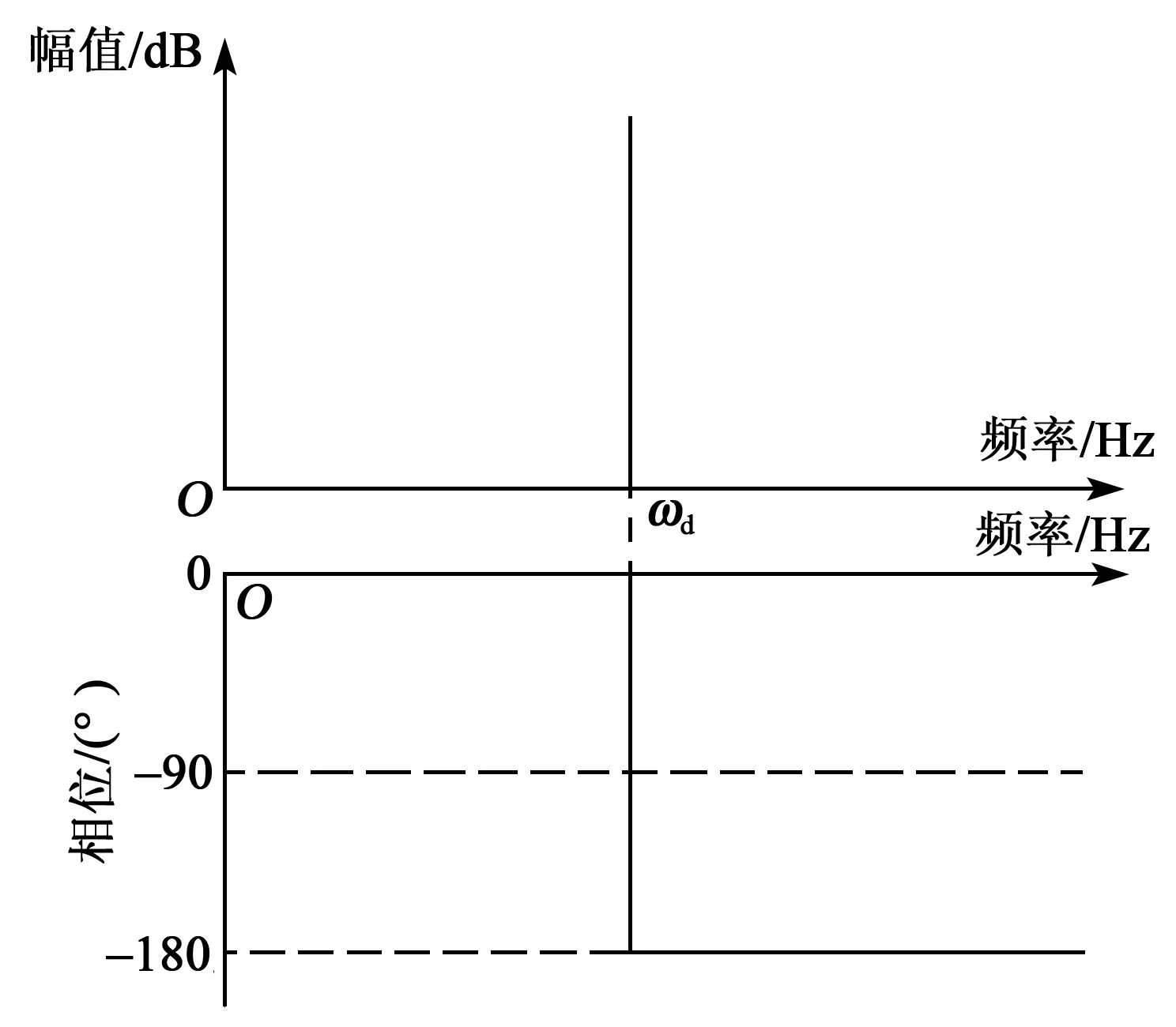
图3 驱动模态频率特性曲线

由图3可知，驱动模态具有选频锁相特性，只有当驱动信号频率等于ωd时，振幅最大，且此时相位差锁定在90°，驱动信号频率偏离ωd时，振幅急剧下降。

1.3 陀螺等效电学特性

对式(7)两边求导可得到驱动模态振动速度方程：

(11)

图4为电导、电感、电容并联(GLC)电路模型。

图4 GLC电路模型

图4所示电路模型的电路方程为

(12)

根据式(11)与式(12)形式上的相同性，可以用图4所示的GLC电路模型等效代替陀螺驱动模态的动力学模型来对陀螺驱动电路进行分析，其等效关系如表1所示。

表1 动力学与电学模型等效关系

根据表1中参数的对应关系，在电路仿真软件中建立陀螺驱动模态等效的GLC电路模型，为了验证陀螺驱动模态的频率特性，给等效电路模型施加一个幅值不变、频率逐渐增加的驱动信号进行交流小信号分析，得到的仿真结果如图5所示。

图5 交流小信号分析结果

由图5(a)可知，当驱动信号频率等于驱动模态谐振点237.11 Hz时，为振幅最高点，驱动信号频率偏离谐振点237.11 Hz时，振幅会急剧下降。由图5(b)可知，当驱动信号频率等于驱动模态谐振点237.11 Hz时，输出电压信号的相移几乎为0，驱动信号频率偏离谐振点237.11 Hz时，振动速度信号相位差会分别趋于90°和-90°。而陀螺振动速度信号与振动位移信号存在-90°的相移，故等效电学模型的交流小信号分析结果与动力学模型分析结果一致。

2 闭环驱动系统实现与分析

2.1 闭环驱动系统实现

基于驱动模态的理论分析，设计了振弦式陀螺的锁频稳幅闭环驱动系统。其原理如图6所示，共分为两部分，即

1) 基于相位负反馈原理的频率控制环路，通过锁定90°相位差，快速追踪陀螺驱动模态的固有频率。

2) 基于可变增益控制(AGC)原理[12]的幅值负反馈控制环路，调节驱动信号的幅值稳定，从而实现陀螺的谐振稳幅驱动。

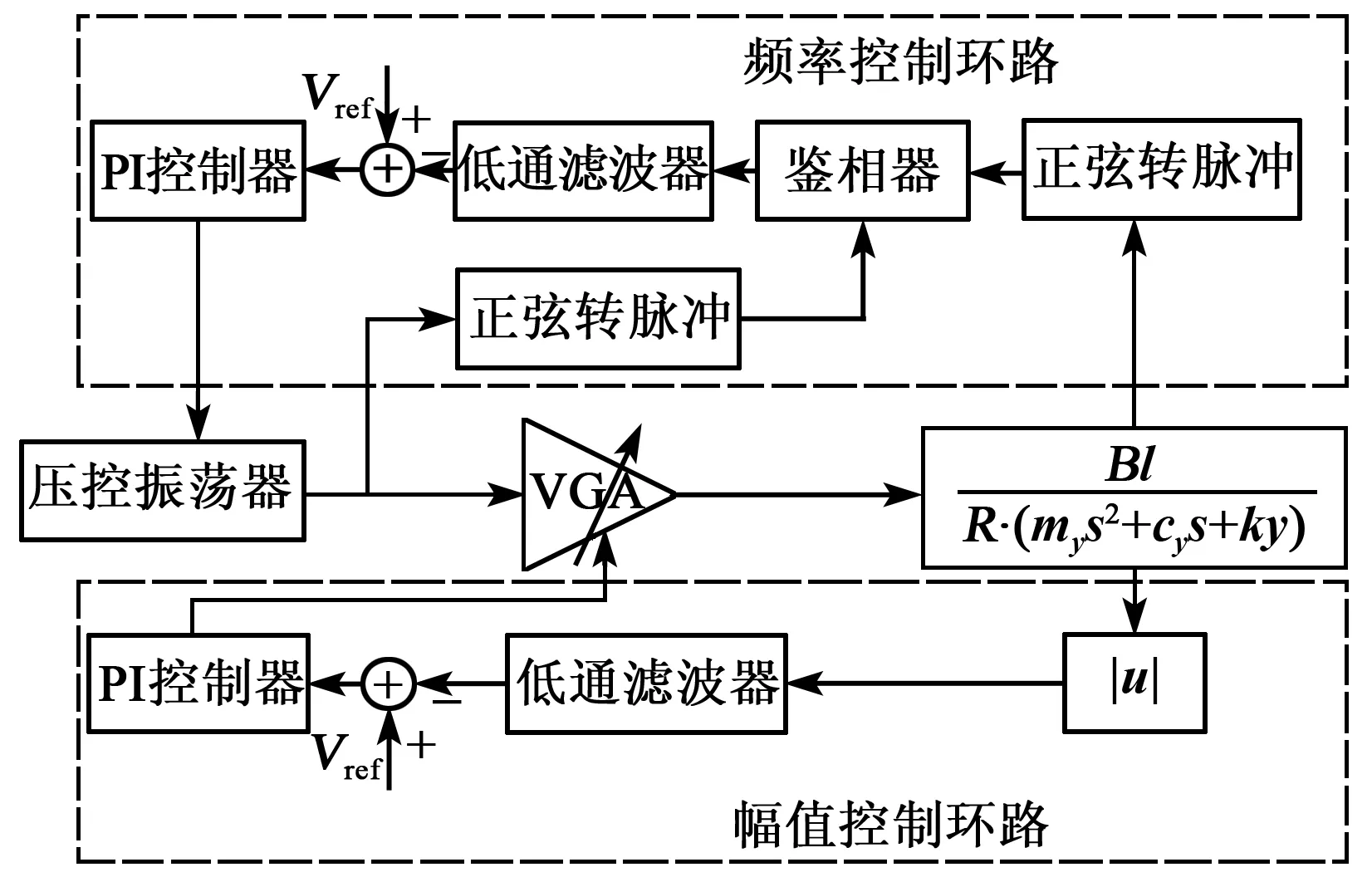
图6 闭环驱动系统原理图

在频率控制环路中，将驱动信号和驱动模态振动位移信号分别转换成同频率50%占空比的正脉冲信号，输入鉴相器(PD)得到驱动信号与振动位移信号的相位差信号，经过低通滤波后与参考相位差信号相比，若比参考相位差信号小，则比较器输出为正，PI控制电路的输出电压会逐渐增大，从而增大VCO的输出频率，反之，则会减小压控振荡器的输出频率，直到驱动信号与振动位移信号的相位差等于参考相位差90°，此时PI控制电路输出保持不变，驱动信号频率稳定在驱动模态固有频率。

幅值负反馈控制环路利用陀螺振动反馈信号的峰值信号通过PI控制器调节可变增益放大器(VGA)的增益系数，从而实现对VCO输出信号的增益控制，当陀螺振动信号幅值大于参考幅值时，PI控制电路输出减小，增益系数减小，反之，增益系数增大，直至振动位移信号的幅值稳定在设定的参考幅值，增益系数不变，从而实现驱动信号的稳幅控制[13]。

2.2 系统仿真与分析

根据闭环驱动系统锁频稳幅原理，在Matlab/Simulink仿真软件中建立闭环驱动系统，其中PD采用XOR逻辑模块实现，其电路实现简单且可以线性反映0°～180°的相位差，陀螺驱动模态则采用其对应的传输函数等效替代。其闭环驱动系统模型如图7所示。

图7 闭环驱动系统Simulink模型

为了验证陀螺因外界环境影响导致陀螺的ωd发生改变时相位负反馈驱动系统锁频稳幅性能，采用中心频率为237 Hz的驱动系统分别对固有频率不同的驱动模态进行驱动仿真，ωd分别设置为287 Hz、257 Hz、237 Hz、217 Hz、187 Hz。图8为驱动信号频率特性图。由图可知，通过相位负反馈调节频率是一个逐渐稳定的过程，仿真结果表明，ωd偏离设置的中心频率，会略微延迟频率锁定时间，但总体上均在0.2 s内实现频率追踪，且频率抖动低于0.021 73 Hz，1 s后频率完全稳定时，频率抖动低于0.011 37 Hz。

图8 不同固有频率下的锁频特性图

图9为驱动模态振动位移的振幅特性图。结果表明，5种不同固有频率的驱动模态均能在0.4 s左右将幅值控制在设定值，且幅值抖动小于0.013 31 V,当系统在2 s后完全稳定时，幅值抖动可控制在10-9V以内。

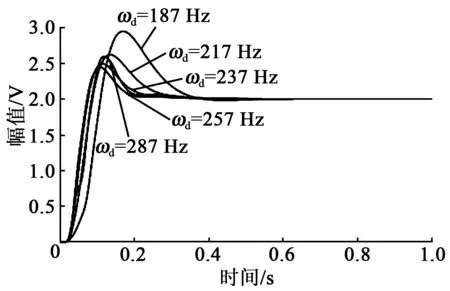
图9 不同固有频率下的稳幅特性图

3 驱动电路实现与仿真

3.1 正弦转脉冲电路

正弦转脉冲电路实际上是一个施密特触发器电路，利用施密特触发器状态转换过程中的正反馈作用，可以将周期性信号变换为边沿很陡的矩形脉冲信号，其结构主要由两级反相器74LS04串联构成，同时通过分压电阻将输出端的电阻反馈到输入端。其前置的过零比较电路的作用是将微弱的振动输入信号放大。其电路如图10所示。

图10 正弦转脉冲电路

3.2 PI控制电路

图11为一种镜像对称型PI控制电路，通过建立对称网络可以消除部分电容、电阻引入的误差。

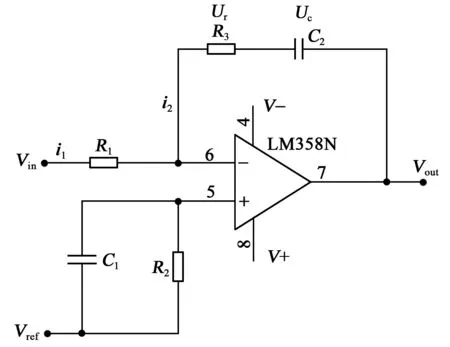
图11 镜像对称型PI控制电路

其PI控制表达式为

(13)

由式(13)可知PI控制电路的比例积分运算形式，其中负号表示输入与输出信号相位相反，R3/R1为PI控制电路的比例系数，R1C2为PI控制电路的积分时间常数，当R1不变时，可分别通过改变R3和C2的值实现PI控制参数调整。

3.3 压控振荡电路

压控振荡电路采用LM566CN芯片实现。图12为压控振荡电路连接图，通过改变C2的值即可改变VCO的灵敏度。由于LM566CN输出的振荡信号存在直流分量，增加二阶高通滤波器和二极管限幅电路对振荡信号进行滤波和整形，从而得到高质量的方波信号。

图12 压控振荡电路

3.4 整流电路

图13为精密整流电路，当正弦信号处于正半波期间时，运算放大器U1的反向输入端等效为断路，正半波信号会流向二极管D1，此时D1导通，D2不导通，同时输入的正半波会通过R4被送入U2的同向输入端，此时D3和D4均导通，整个电路相当于电压跟随器。当正弦信号处于负半波期间时，U1输入负半波，D1不导通，D2导通，U2也输入负半波，D3导通，D4不导通，此时整个电路相当于反相器电路。

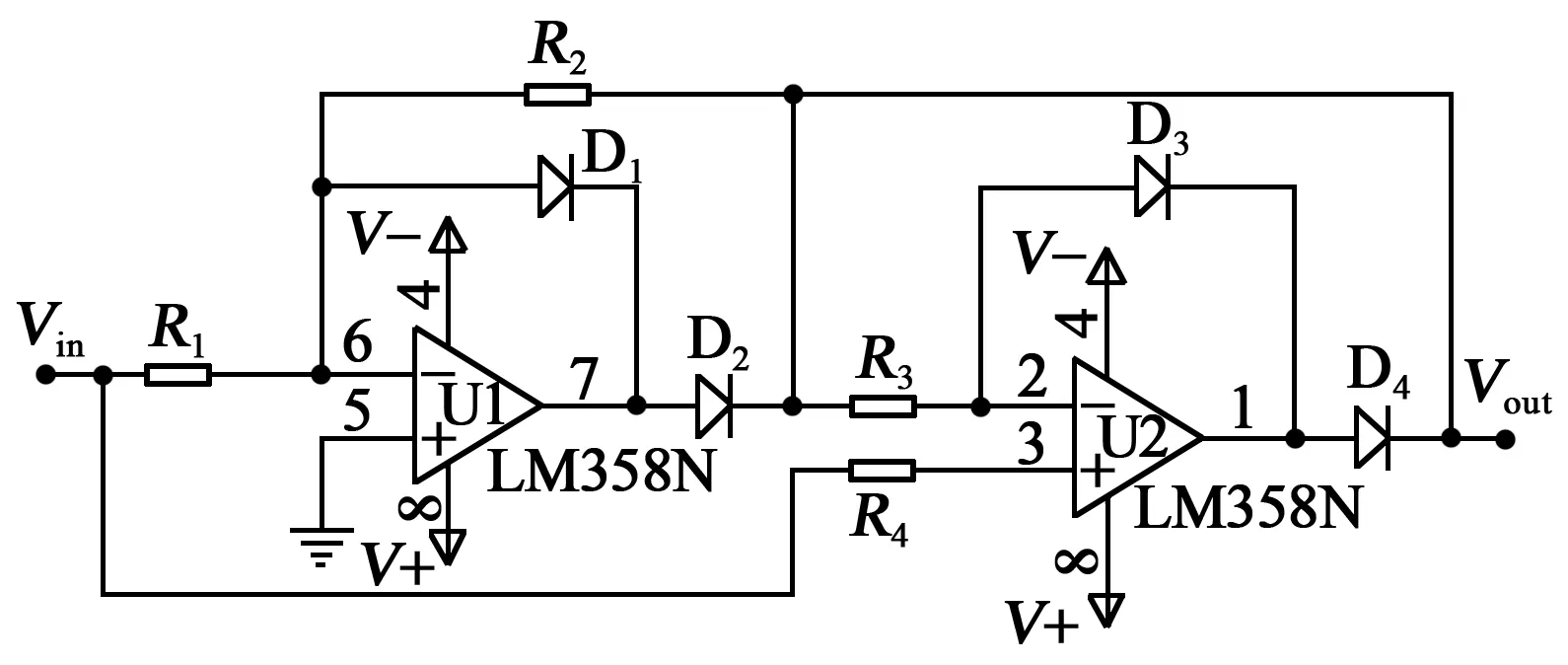
图13 精密整流电路

3.5 完整闭环驱动电路仿真验证

将设计的各电路模块通过ptoteus电路仿真软件连接成完整闭环驱动电路，针对固有频率为237.11 Hz的陀螺驱动模态等效电路模型进行器件级电路驱动仿真，图14为VCO输入的控制信号，其可以反映驱动信号的频率变化。图15为陀螺驱动模态的振动反馈信号，其可以反映陀螺驱动模态等效电学模型的起振情况。

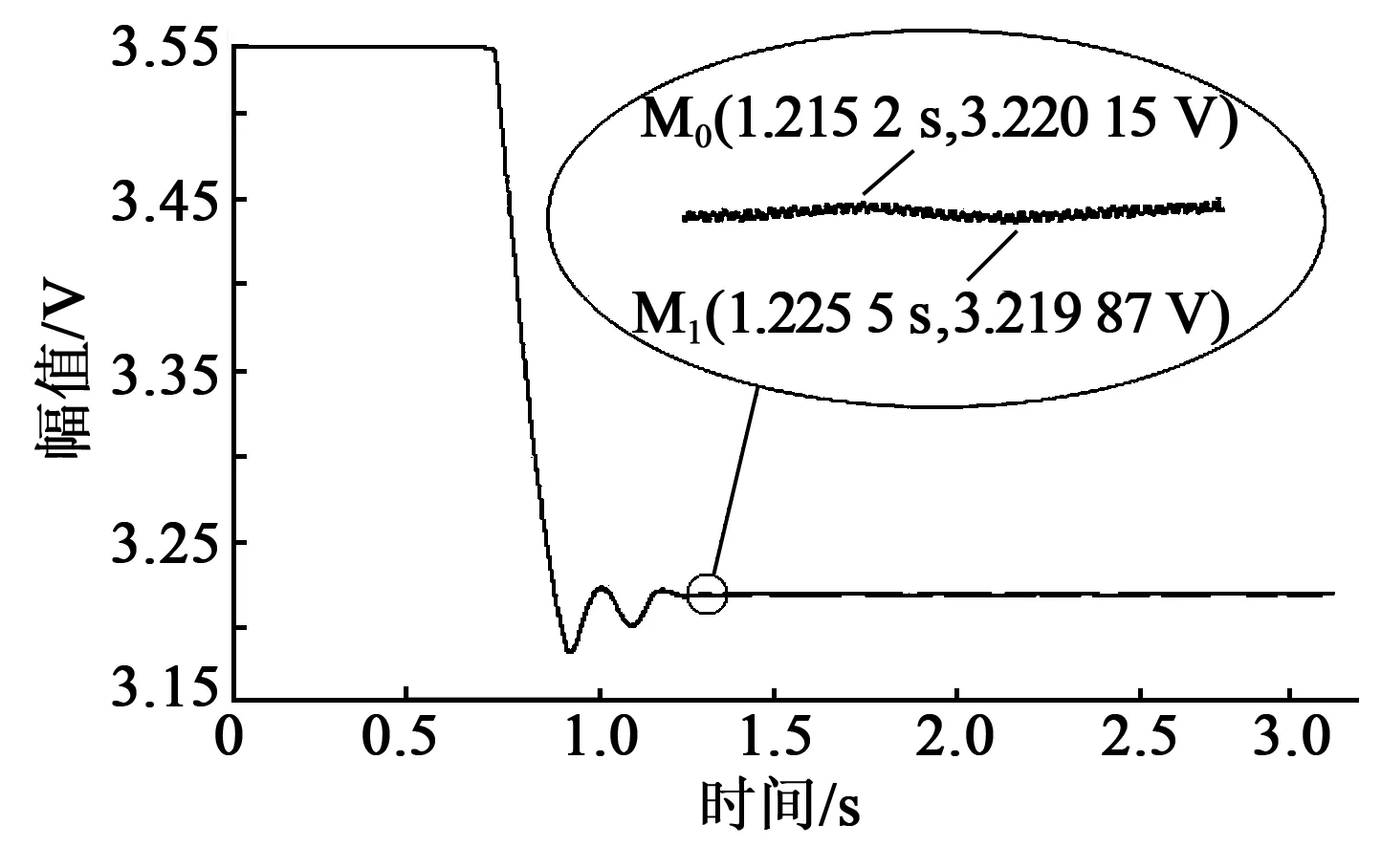
图14 VCO控制信号

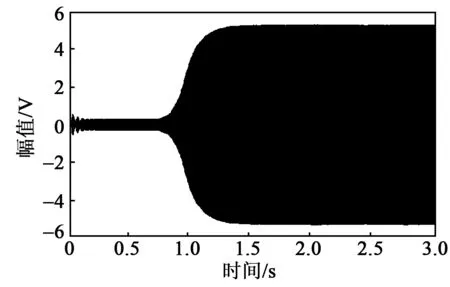
图15 陀螺振动反馈信号

图14、15的仿真结果表明，闭环驱动电路能够实现陀螺固有频率追踪和幅值稳定，频率稳定时间约为1.2 s，陀螺稳幅起振时间约为1.5 s，频率稳定后VCO的控制电压为3.220 1 V，幅值抖动小于0.000 28 V，结合VCO的敏感度为73.6 Hz/V，可以计算出驱动信号频率为236.992 Hz，频率偏差为0.118 Hz，频率抖动小于0.020 6 Hz。

4 完整闭环驱动电路测试

将设计的各电路模块连接成完整闭环驱动电路，搭建印制电路板对振弦式陀螺进行驱动测试，图16为闭环驱动电路测试版图。

图16 闭环驱动电路测试版图

系统加电后，通过考察压控振荡器的输入信号(见图17)可知，由于PI控制电路的起始输出为运算放大器的高电平，而非为0，从而使压控振荡电路的输入信号在系统刚启动时也为运算放大器的高电平，在频率控制环路的作用下，系统在2 s内实现了频率追踪锁定，振荡频率为237.112 Hz。

图17 压控振荡器控制电压

通过考察陀螺驱动后的振动反馈信号(见图18、19)可知，驱动系统能在2 s实现陀螺起振，且陀螺稳定后振动反馈信号的峰值为6.16 V，经过全波整流后的有效值与设定的4 V直流参考电压基本一致，从而验证了幅值控制环路的稳幅性能。

图18 陀螺驱动起振过程

图19 陀螺稳定后的振荡信号

5 结束语

在对振弦式陀螺驱动模态理论分析的基础上，设计了一种相位负反馈驱动电路系统。利用Simulink系统仿真软件分析了系统的锁频稳幅性能，结果表明，该驱动电路系统在驱动模态固有频率发生大幅偏差时，能够快速追踪其固有频率并实现稳幅振动，频率抖动小于0.011 37 Hz，幅值抖动小于10-9V。对完整闭环驱动系统进行了器件级电路设计与仿真，仿真结果表明，陀螺稳幅起振时间约为1.5 s，频率抖动小于0.020 6 Hz。最后将闭环驱动电路制作成实物后对陀螺进行驱动测试。测试结果表明，该驱动系统能够在2 s内实现陀螺频率锁定与幅值稳定，稳定后陀螺振动频率为237.112 Hz，振动幅值与设定参考值一致，验证了闭环驱动电路的锁频稳幅驱动性能。并且该驱动电路实现简单，具有很好的适用性与研究前景。