人口结构、人口质量与产业结构转型升级——基于PVAR模型的实证分析

赵茂林，李 鹏

（安徽财经大学 经济学院，安徽 蚌埠233030）

一、引言与文献综述

近年来，我国经济发生了许多新的变化，主要表现在经济增速放缓、经济结构优化调整，由此国家提出经济要高质量发展。经济高质量发展就要处理好经济结构问题，处理好三大产业之间的关系以满足不同经济发展阶段的需求，优化产业结构，促进产业结构转型升级。此外，我国人口结构也发生了显著的变化，老龄人口在总人口中的比例增加，人口出生率降低，劳动力供给减少，人口红利降低，福利性支出增加，这又会减缓经济结构转型升级的速度，对经济结构转型升级产生不利影响。已有的文献研究多站在人力资本整体水平角度分析其对产业结构转型升级的影响，而很少关注人力资本结构的因素，此外，基于人口结构和人口质量的角度分析人力资本对产业结构转型升级的文献更少。

国外关于人口因素对产业结构转型升级的研究主要从人力资本角度，将人力资本因素融入经济增长动因之中，研究人力资本在促进经济增长和优化产业结构中的作用机制。如Robert Solow（1956）[1]认为人口是一国经济持续增长的决定性因素；R.E.Lucas（1989）[2]进一步认为一个国家的经济增长和产业持续发展的动力来自人力资本的不断积累；Brock G&German-Soto V（2013）[3]从劳动者的技能和生产效率两方面的提高描绘人力资本提升，由此推断出人力资本提升能够促进经济增长，优化产业结构。

国内关于人口因素对产业结构转型升级的研究主要从人力资本角度和人口红利角度进行。张国强等（2011）[4]研究了我国东部、中部、西部以及国家层面的人力资本与产业结构转型升级的关系，论证了不同地区人力资本水平不同，以及人力资本能有效提升我国产业升级[4]。同样是研究我国东部、中部、西部以及国家层面人力资本与产业结构之间的关系，刘忠璐、刘榆（2015）[5]更细致地论证了人力资本能促进产业向高级化方向发展。此外，周光锋（2012）[6]的研究表明人力资本优化导致我国劳动密集型产业占比逐渐减少，而知识和技术型产业占比逐渐增加。基于人口红利角度的研究，孟令国（2013）[7]以广东省为例，分析人口结构对储蓄率的影响进而影响产业结构，提出要加快产业结构转型升级；李豫新、程谢君（2017）[8]基于西部地区的面板数据，分析了人口年龄结构变动的消费效应，进而得出老龄化人口有利于医疗卫生产业的发展，加快消费的增长，有利于消费结构的优化，进而促进经济结构的优化。

结合上述研究成果，本文借鉴徐诺金（2018）[9]关于人口结构和人口质量的分析，结合我国31 个省份2001—2016年的面板数据，基于人口结构和人口质量两方面的指标，采用面板向量自回归（PVAR）模型，实证分析人口结构、人口质量与产业结构转型升级之间的动态关系。

二、基于新古典理论的研究框架

本文基于新古典理论的研究框架分析人口因素对产业结构转型升级的影响，采用索洛模型，同时采用柯布—道格拉斯生产函数形式：

其中，投入要素为劳动L和资本K，对式（1）两边取对数，可得：

其中，α、β 分别表示劳动和资本的产出弹性。对式（2）进一步化简则可以得到增长率表达式：

式（3）表明，在简化的经济模型中，代表技术进步率的GA、代表劳动投入增长的GL和代表资本投入增长的GK构成了经济增长GY。陆旸、蔡昉（2016）[10]以上式为基础，分析了人口年龄结构对经济增长的影响，其中以劳动年龄人口的抚养比为人口年龄结构的代理变量，进而分析其对经济增长产生的影响。基于上述类似的分析思路，结合本文的研究问题，选取一个或多个代表人口因素的代理变量，分析人口结构和人口质量对产业结构转型升级的影响。本文选择三个关于人口结构和人口质量的代理变量，分别用X、Z、R表示，则用以分析人口因素对经济增长产生的影响的式（3）就可以转换为如下方程：

由于本文对全国31个省份的2001—2016年的相关数据进行分析，使用的是面板向量自回归模型，所以上述式（4）需要进行分省面板回归以克服时间序列数据太短带来的估计不准确问题，因此，得到下式：

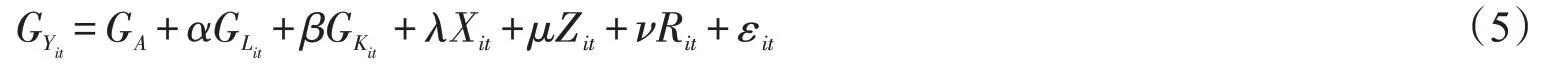
为了验证人口因素对产业结构转型升级的影响，本文对经济增长做数学上的分解并参考了干春晖等（2011）[11]的分解方式，具体如下：

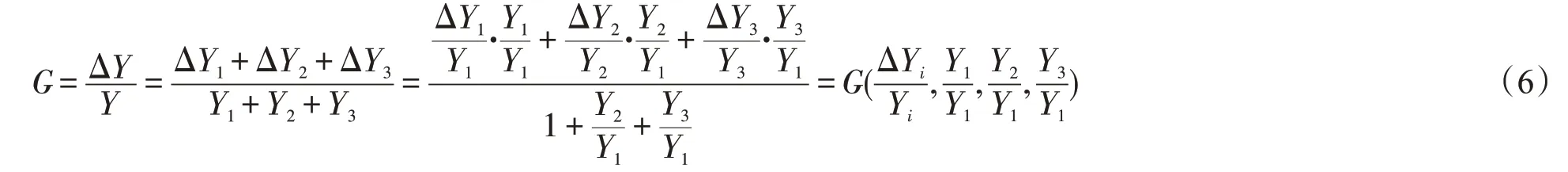
其中，ΔY/Y 、ΔYi/Y 和Yi/Y1分别表示一个经济体的总增长率、第i 产业的增长率和第i 产业收入与第一产业收入的比例关系。式（6）最后还可以理解为经济增长与产业增长和产业结构变动的关系，即随着经济变动，产业结构形态也要发生相应的变动，而经济增长最终导致产业结构升级形态与经济增长一致。

三、模型构建

（一）指标选取和数据来源

产业结构转型升级指标。从已有的文献整理可得关于经济结构升级的指标有Herfindahl Index（HI）、Lerner Index（LI）、Rumelt等，国内学者采用的经济结构转型升级指标主要有两类。

徐德云（2008）[12]建立产业结构升级指数（R）来衡量产业结构升级：

其中，yi=Yi/Y 表示第i 产业产值在总产值之中所占的比重，所以R 的取值范围为[1，3]，如果R 取1或接近1的值，表示该经济体中产业结构层次较低，经济社会是以农业为主的农耕社会，第二、三产业所占比重很小，经济水平很低；如果R 取3或者接近3的值，表示该经济体中产业结构层次较高，经济社会是一种工业化社会或者是知识服务型社会；如果R 取2或者接近2的值，表示该经济体产业结构处于前两者之间。

干春晖等（2011）[11]则建立了如下的产业结构升级指数（is）：

其中，Y2、Y3分别表示第二产业和第三产业增加值之和，is 值越大，意味着经济水平越高，产业结构越好。本文主要分析人口因素与产业结构转型升级之间的关系，侧重分析人口对产业结构优化的影响，因此选取is 建立产业结构转型升级指数。

人口指标包括人口结构变量和人口质量变量。其中，人口结构变量包括总抚养比（raise）和非农就业占比（labor）两个指标。

选择总抚养比（raise）作为人口结构变量指标之一，衡量人口因素对产业结构转型升级的影响，这一指标是基于王德文、蔡昉、张学辉论证总抚养比对经济增长的边际效应而来。总抚养比（raise）衡量的是经济活动中劳动人口和非劳动人口之间的相互关系，是对人口年龄结构的测度，可表示为少儿抚养比和老人抚养比的加总。一般而言，总抚养比与经济增长的关系是反向的，抚养比低意味着人口为经济增长提供较好的条件，更有助于经济结构转型升级，抚养比高则意味着人口条件较差，劳动人口缺少，阻碍经济结构转型升级。

人口结构变量另一个指标是非农就业占比（labor），该指标基于孙建、周兵（2008）[13]采用SEM模型分析了经济体中产业结构和就业结构之间的关系而得来，指的是经济体的就业人口中第二产业和第三产业人口占总人口的比例，是对经济体的就业结构的测度。通常情况下，非农就业人口占比的值越大，意味着经济发展越好，产业结构也更加合理，反之亦然。

人口质量变量：平均受教育年限（edu）。该指标度量了国民平均受教育的程度，是人力资本投资的主要组成部分，是人口质量变量的主要代理因素。人口的平均受教育程度越高，其知识水平越高，能胜任的工作难度与复杂度越高，越能适应高端行业，所以人口受教育程度越高，经济增速越快，产业结构也就越合理，反之越不利于产业结构的优化。

本文的数据主要来自两部分，一是统计年鉴的数据，二是对国家统计局数据的整理，具体来源如下：产业结构转型升级指数（is）来自《中国统计年鉴》；总抚养比（raise）、非农就业占比（labor）和平均受教育年限（edu）由国家统计局统计数据而得，缺失数据值采用回归替换法处理，在进行模型设置之前，需要对数据进行对数化处理。变量及其描述性统计见表1。

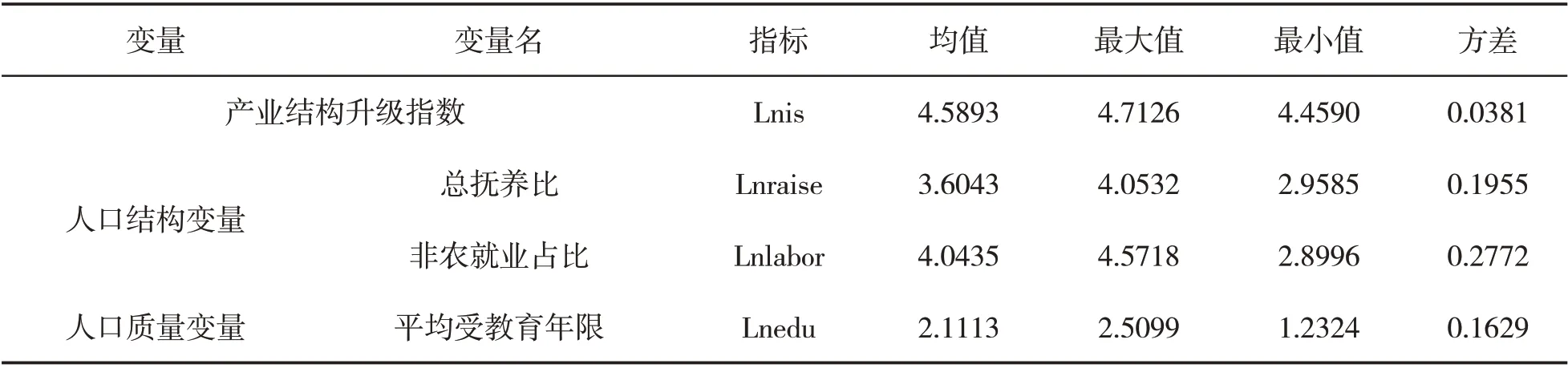
表1 变量及其描述性统计

（二）模型设置

应用面板向量自回归（PVAR）模型，利用2001—2016年省级面板数据来验证人口因素与产业结构转型升级的关系。Holtz-Eakin等（1988）[14]第一次提出PVAR模型，后续经过完善发展，逐渐成熟。相较于VAR模型，PVAR模型既可以将模型中的变量都视为内生变量，不同变量之间的影响通过脉冲响应函数表达，而且，PVAR是以面板数据为样本，增加了截面个体的数量，扩大了样本总数量。在PVAR模型中，假设时间序列的长度为T，滞后性的阶数为m，当T≥m+3时，可以对模型的参数进行估计，当T≥2m+2时，可估计稳态下的滞后性参数。基于此，本文建立如下的PVAR模型：

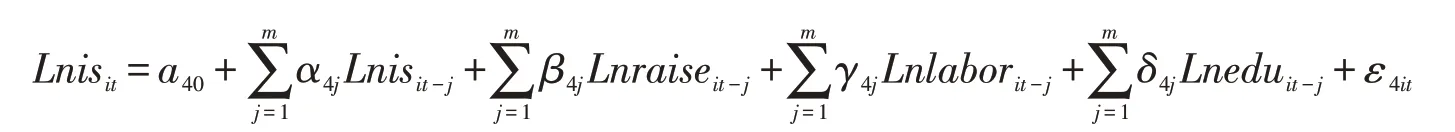
其中，i 表示不同的省份，t 代表时间，j 代表滞后阶数，isit表示第i 个省份第t 年的产业结构升级指数；raiseit表示第i 个省份第t 年的总抚养比；laborit表示第i 个省份第t 年的非农就业占比；eduit表示第i 个省份第t 年的平均受教育年限；ε1it、ε2it、ε3it、ε4it分别为方程的随机误差项，a10、a20、a30、a40为不同省份的个体异质性，α、β、γ、δ 代表滞后变量的参数值。为避免截面个体差异性而带来的固定效应和对截面个体产生影响的时间效应，本文采用Love I&Zicchino L（2007）[15]所使用的PVAR模型的Stata程序，即前向均值差分法（Helmert）和组内均值差分法（Mean-Differencing）两种方法。同时为使得广义距估计法（GMM）对模型参数进行有效估计，本文也采用了连玉君的PVR2软件包进行估计。

四、实证分析

（一）单位根检验

考虑到模型估计中可能存在的伪回归现象，在对模型参数的估计之前，需要对数据进行单位根检验。本文采用了LLC、IPS、ADF-Fisher、PP-Fisher方法分别对面板数据进行检验，检验过程由Stata 12.0完成，检验结果见表2。经检验，各指标变量在相应的显著性水平下均原水平平稳。

表2 面板单位根检验结果

（二）模型的滞后项选择

根据模型滞后阶数的选择标准结合表3，本文将最优滞后阶数设置为3。

表3 PVAR模型最优滞后阶数的确定

（三）动态面板数据GMM估计

由上文分析可建立滞后阶数为三阶的PVAR模型，将人口结构变量中的总抚养比、非农就业占比及人口质量变量中的平均受教育年限和产业结构转型升级指数作为PVAR模型的内生变量，通过使用Stata 12.0并采用广义距估计法（GMM）对模型参数进行有效估计。本文的分析重点考察的是产业结构转型升级和人口因素之间的关系，具体结果见表4。

表4 PVAR估计结果

当被解释变量为产业结构转型升级指数时，在5%的显著性水平下，其自身滞后一期水平对当期水平影响表现得较为显著，滞后三期水平对当期在1%的显著水平下显著，说明产业结构升级对自身有很好的促进作用。同时，滞后三期的总抚养比在10%的显著水平下显著性一般，而且为负值，说明总抚养比对产业结构转型升级的影响在滞后三期的时候并不明显，表现出抑制作用。非农就业占比和平均受教育程度在滞后一期的水平上，对产业结构转型升级的影响表现得并不显著，而在滞后二期的时候，非农就业占比对产业结构转型升级的影响为负值，这可能和劳动力转移不满足产业结构转型升级的要求有关，即低端劳动力的供给虽然较为充足，但满足不了产业结构转型升级对高端劳动力的需求。在滞后三期水平的时候，非农就业人口和平均受教育年限对产业结构转型升级的影响均为负，这一方面说明劳动力市场供需不匹配带来的产业结构转型升级滞后的问题，另一方面也说明非农就业人口和平均受教育年限对产业结构转型升级的影响在短期内显示不出来，这为政策的制定提供了借鉴意义。

当总抚养比、非农就业人口、平均受教育年限分别作为被解释变量时，可以看出，产业结构转型升级在滞后一期水平和滞后两期水平的时候对总抚养比、非农就业人口、平均受教育年限的影响均不显著，这可能和产业结构转型升级的所处阶段有关，当产业升级处于上升期的时候，对人口的质和量都有很大的需求，且这种需求不仅可以通过市场的供给，而且产业的升级也促进了人口素质的上升。当产业结构转型升级滞后三期时，其对总抚养比影响为负，非农就业人口在1%的显著水平下有负显著影响，对平均受教育年限在10%的显著水平下有较强的影响。

（四）脉冲响应函数

脉冲响应函数考察的是给内生变量一个冲击时所产生的影响，这能更好地刻画模型中内生变量之间的关系。在进行脉冲响应函数分析之前，先进行稳定性检验。特征多项式根的倒数都落在单位圆之内，表5表明特征多项式的系数均小于1，检验结果表明PVAR模型是稳定的。

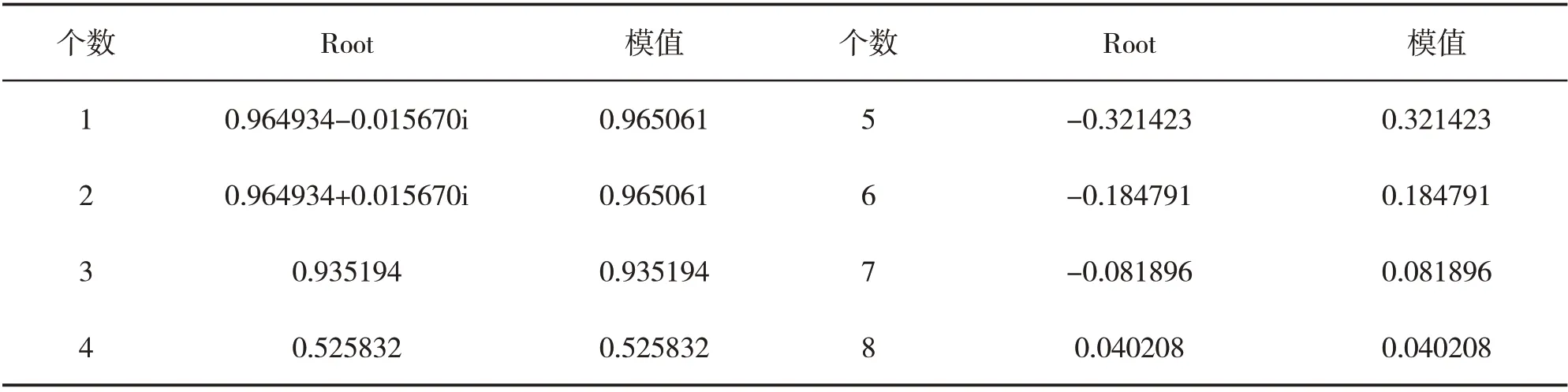
表5 模型稳定性检验结果

上文分析了PVAR模型的稳定性，证明PVAR模型具有进行脉冲响应函数分析的条件，为了得到脉冲响应结果，采用蒙特卡罗模拟方法进行分析。如图1所示。其中，实线为脉冲响应函数曲线，两条虚线围成的部分为置信区间带，每个图的标题代表前者一个标准差的冲击对后者产生的影响。

图1 脉冲响应函数

由脉冲响应函数第1 行可知，给产业结构转型升级（Lnis）一个标准差的冲击，对自身的影响在当期为0.03，然后逐渐减少，在第六期的时候趋于0；对总抚养比在第一期影响为0，然后逐渐递增，在第二期达到最大约为0.003，紧接着开始影响降低，在第三期的时候趋近于0；对非农就业占比的影响一开始为0，然后影响逐渐增大，在第二期的时候约处在0.0025的水平上并一直持续下去；对平均受教育年限在第一期的影响为0，然后稳定增长至第一期约为0.0025并持续保持下去。以上的值均为正，说明产业结构转型升级除了对自身有正的影响外，对总抚养比、非农就业占比、平均受教育年限的影响也为正。

由脉冲响应函数第2行可知，给总抚养比（Lnraise）一个标准差的冲击，会在当期对产业结构转型升级产生正的影响，随后影响逐渐降低，在第二期和第三期之间保持平稳，然后上升并回到第一期的水平上；对自身的影响在当期为0.05左右，然后逐渐下降，在第六期的时候趋于平缓；对非农就业占比的影响在当期为0，然后下降为负值，并持续处于负值状态；对平均受教育年限的影响在当期为0，然后逐渐增大，并在第三期后处于较稳定状态。以上的值有正有负，总抚养比除了对自身产生正的影响，对产业结构升级、平均受教育年限也会产生影响，而且其影响为正，而对非农就业占比则会产生负的影响。

由脉冲响应函数的第3行可知，给非农就业人口（Lnlabor）一个标准差的冲击，在当期会对产业结构转型升级产生影响而且影响为负，随后影响虽有所提高，但还是处于负值水平，在第二期以后持续下降并在第三期处于较稳定影响状态；对总抚养比的影响在第一期时为负，随后波动至0值水平线并保持在略低于0值的负值状态；对自身的影响在当期为正，约为0.03，然后持续下降，但始终处于正值水平；对平均受教育年限的影响并不大，只处于水平线之上，略高于0值。以上的值表明非农就业人口对产业结构转型升级、总抚养比产生影响且值为正，对自身和平均受教育年限产生的影响值为负。

由脉冲响应函数的第4行可知，给平均受教育年限（Lnedu）一个标准差的冲击，在当期会对产业结构转型升级产生正的影响，然后下降至第二期约为0.005，随后上升至第三期后持续下降；对总抚养比的影响在当期为负值，随后虽然有所上升，但一直保持在负值水平并在第五期趋于稳定状态；对其自身的影响在第一期时约为0.03，随后持续下降，并在第五期时接近水平线0值。以上结果表明平均受教育年限对产业结构转型升级、非农就业占比、自身会产生影响且值为正，对总抚养比的影响为负。

（五）方差分解

为了考察产业结构转型升级、总抚养比、非农就业人口、平均受教育年限之间的相互影响程度，可以用方差分解进一步评价各个冲击的重要性。本文列举了三个预测期内的方差分析结果，分别为第10个、第20个和第30个预测期，结果见表6。

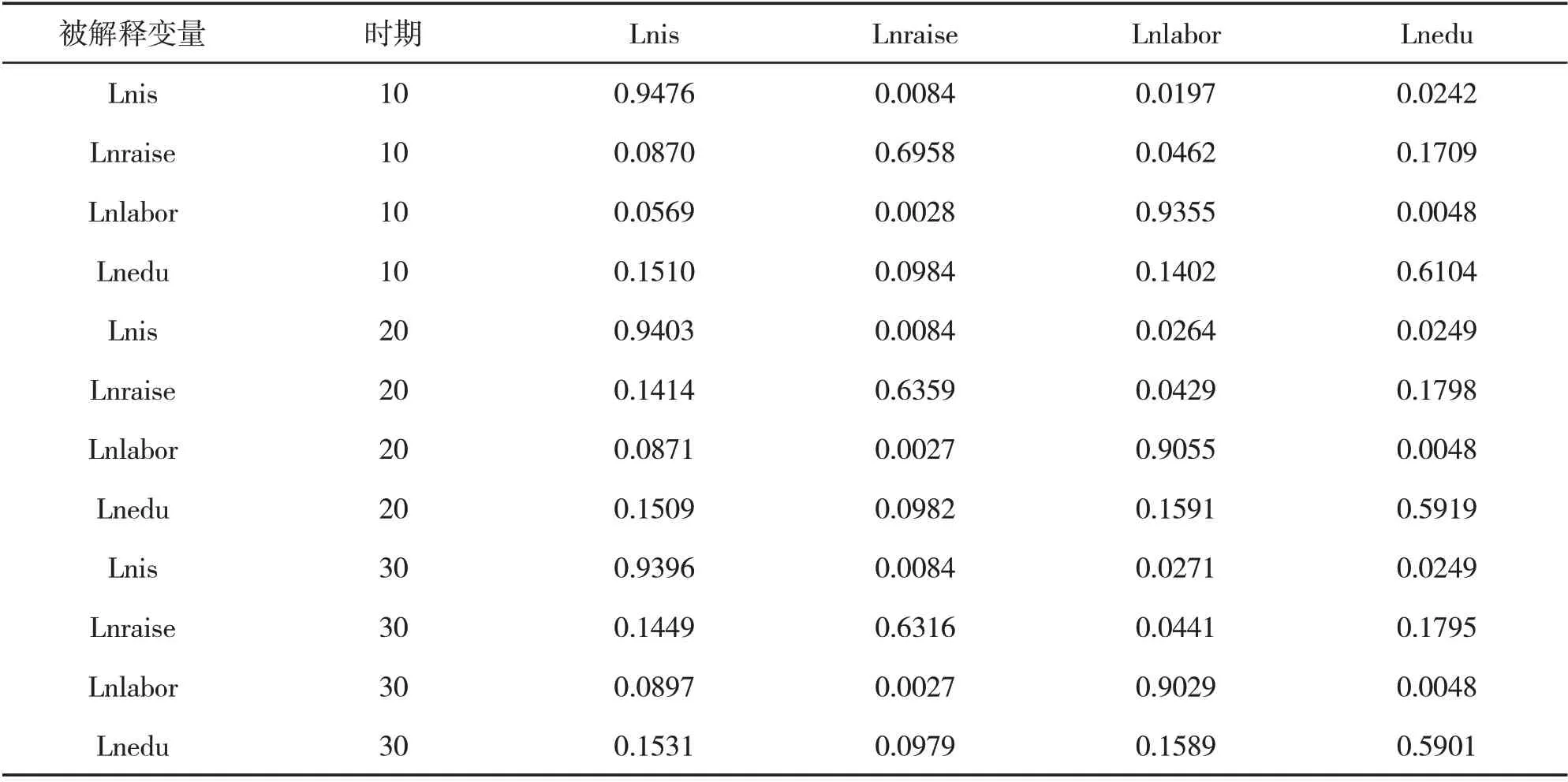
表6 方差分解

由表6分析结果可以看出，10期、20期和30期各变量的解释程度基本一致，可以认为各变量对所有变量误差项的解释程度基本保持不变，故在此以第10期结果为例进行分析。可以看出的是各变量的波动主要受自身的影响较大，受其他变量的影响较小。对于产业结构转型升级的稳健性波动主要来自自身和平均受教育年限的影响，其中，产业结构转型升级变动有94.76%的波动由自身变动解释，仅有2.42%的波动来自平均受教育年限，说明产业结构转型升级的稳健性波动虽然受平均受教育年限的影响，但影响程度很小。对于总抚养比的稳健性波动主要来自自身和平均受教育年限的影响，其中，总抚养比变动有69.58%的波动由自身变动解释，有17.09%的波动来自平均受教育年限，说明产业结构转型升级的稳健性波动虽然受平均受教育年限的影响，但是其对平均受教育年限的稳健性依赖程度较低。对于非农就业占比的稳健性波动主要来自自身的影响，有93.55%的波动由自身变动解释，其余的波动被其他三个内生变量承担。对于平均受教育年限的稳健性波动主要来自自身和产业结构转型升级、非农就业人口的影响，其中，平均受教育年限有61.04%的波动来自自身，有15.1%的波动来自产业结构转型升级，有14.02%的波动来自非农就业人口占比，说明平均受教育年限的稳健性波动在较大程度上依赖产业结构转型升级和非农就业人口占比的稳健性。

五、结论

本文通过建立全国31个省份的PVAR模型，分析了人口结构、人口质量与产业结构转型升级之间的关系。研究发现，产业结构转型升级受其自身的影响较大，表明产业自身的积累有利于产业结构转型升级，这在一定程度上反映了中国近年来经济高速发展背后的产业支撑因素。同时可以看出总抚养比对产业结构转型升级的影响较为明显且为负值，说明较低的总抚养比有利于劳动力的转移，进而促进产业结构转型升级。而非农就业人口和平均受教育年限对产业结构转型升级的影响并不显著，本文认为这可能有两点原因：一是本文考察的产业结构转型升级指的是第二产业和第三产业在经济体中所占的比重提高，更准确地说，第二产业和第三产业中“高端”层次占比提高，这导致劳动力供给与劳动力需求之间存在“空心地带”，从而不利于产业结构转型升级；二是教育程度提升虽然有利于人口整体素质的提高，但是产业结构转型升级是一个长期的过程，短期效果并不是很明显，这需要重视教育的长期效应，而不是短期效应。另外，产业结构转型升级对总抚养比、非农就业占比、平均受教育年限都存在一定的影响，具体如下：产业结构转型升级对总抚养比的影响并不显著，这可能和中国的人口政策有关，而产业结构转型升级对非农就业人口占比存在显著影响，说明在产业结构转型升级过程中，产业的转型会创造大量的就业岗位，吸收更多的劳动力，这在一定程度上反映了中国近些年农民工进城务工的现状。同时，产业结构转型升级对平均受教育年限有较为一般的影响，这可能也与产业结构转型升级对就业人口的影响有关：人口大量就业，生活水平提升，自身的素质也可能提升。