铁道客车关键系统的模态规划研究

汤劲松， 王云鹏， 徐 聪

(中车青岛四方车辆研究所有限公司 技术中心， 山东青岛 266031)

铁路的快速发展对铁道客车提出了更高的要求。由于轨道不平顺、轮轨作用、悬挂系统自身特性及有源设备的激励，使车辆产生复杂的振动，甚至引起某些结构的模态耦合共振，对旅客的乘坐舒适度和设备结构的安全性产生不利影响。为了降低激励对车辆平稳性和安全性的影响，隔离车辆内部振动的传递，迫切需要在铁道客车的正向设计过程中，对车辆系统的各个关键模态进行提前规划，以期从根本上解决或衰减各系统的振动。

目前铁道客车的模态研究多集中在转向架构架刚体模态、车体低阶弹性模态及车下设备模态隔振等方面。宫岛、周劲松等[1]利用动力学模型研究了弹性车体与转向架构架的垂向耦合振动；陈迪来、沈刚等[2]基于模糊数学的欧式贴近度准则，定义了整个车辆系统所有模态之间的耦合度，并以降低系统模态耦合度为目标对车辆悬挂参数进行设计；任尊松、刘志明等[3]通过实车测试获得高速动车组各部件的振动特性，并给出了轮轴、构架及车体的主要频率范围；石怀龙、康洪军、曾京等[4-5]基于柔性多体动力学理论，围绕整备状态下车体弹性与车下设备的耦合振动进行研究，并提出两者之间的最佳匹配参数；王金田、贾尚帅、李丰等[6-8]则分析了引起车辆端墙异常振动的原因及车体与车下吊挂设备、座椅的耦合模态振动现象。总体来看，对铁道客车的某一部分或某几部分进行振动模态分析的较多，而对整车系统的模态耦合进行研究的则较少。文中利用仿真手段，通过建立铁道客车刚柔耦合分析模型研究车辆系统关键结构的振动特性，并对其进行模态匹配研究，提出典型铁道客车的模态规划推荐表，从而为类似车型的模态设计提供前期目标导向，尽可能降低后期产生耦合共振的可能性。

1 计算模态分析理论

模态分析是进行铁道客车系统振动及模态匹配研究的基础。模态是结构的固有特性，可以用模态参数(固有频率、阻尼比及模态振型)来表征，这些模态参数能够完整的描述系统的动态特性。模态分析一般分为计算模态和试验模态分析[9]，如果分析过程是用有限元计算的方法，那么则称为计算模态分析，见图1模型。

图1 振动系统

一般来讲，系统是一个连续的线弹性结构，将其离散成一个多自由度系统后，它在物理坐标系中的运动微分方程可变成结构动力学模态分析中的特征值问题。

一个n阶自由度系统的运动微分方程为[10]：

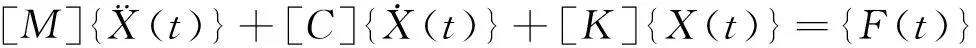
(1)

式中，[M]、[C]、[K]、{F(t)}及{X(t)}分别为系统的质量矩阵、阻尼矩阵、刚度矩阵、载荷向量及响应向量。

假定系统为自由振动并忽略阻尼，则式(1)变成如下的二阶常系数线性齐次微分方程：

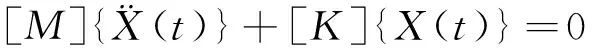
(2)

其中，X(t)是复数，设方程的特解为：

{X(t)}={φ}ejωt

(3)

将特解式(3)代入式(2)，则有：

([K]-ω2[M]){φ}=0

(4)

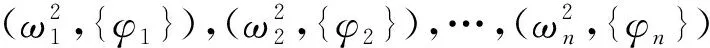
当系统发生振动时，它在任一时刻的运动都是所有正交模态的线性耦合。为便于观察，表现出来的振型幅值都按照归一化方法进行处理。归一化方法一般有3种：

(2)以{φi}TM{φi}=I(i=1,2,…,n)作为归一化原则。根据该原则，计算得到的向量为正则振型；

(3)以模态振型中最大的元素为幅值基准，即设为1。

2 刚柔耦合分析模型

基于某铁道客车的刚柔耦合动力学模型进行研究。柔性体运动方程可由式(5)的拉格朗日方程得到[11]：

(5)

式中，Ψ(ξ,t)为完整约束；ξ为柔性体的广义坐标，包括位移坐标X、欧拉角坐标Ω和模态坐标q*，即ξ=[XΩq*]T；Q为包括有势力在内的广义力；L为拉格朗日函数，即动能与势能之差，L=T-V；λ为待定因子；F为如式(6)的逸散函数，其中，D为瑞利阻尼矩阵。

(6)

根据动能定理和多体动力学理论，得到如式(7)动能表达式：

(7)

其中，质量阵可写成1个3×3矩阵形式：

(8)

式中，t，r，m分别为平移、转动和模态自由度。

采用有限元方法建立整备车体的有限元模型，并将转向架与车体的连接点、车体上的目标点处理成主节点，再利用Guyan矩阵缩减理论对有限元模型进行自由度缩减从而得到车体的弹性体模型[12]，然后再将其导入动力学软件中，利用Rite法将弹性车体的无限自由度缩减为有限振型，弹性体模型上的主节点直接使用bushing、spring、joint等力元或约束与刚体模型进行连接，最终建立整备车辆的刚柔耦合动力学模型，其中转向架为刚体模型。

铁道车辆是一个复杂的多体系统，不但有各部件之间的相互作用和相对运动，而且还有轮轨之间的相互作用关系。因此对结构中的一些次要因素进行相应的假定或简化，而在对动力学性能影响较大的主要因素方面尽可能做出符合实际情况的模拟见图2。在建立计算所用的数学模型时做以下假定[13]：

(1)轮对、构架等部件的弹性比悬挂系统的弹性要小的多，均视为刚体；

(2)考虑了轨道的整体横向、垂向弹性和阻尼；

(3)只考虑单一车辆，不考虑相邻车辆的作用；

(4)假定车辆保持匀速运行。

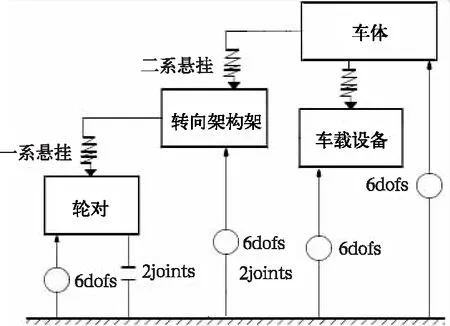
图2 铁道客车力学模型拓扑图

3 系统模态耦合的影响

所谓模态规划即根据各系统间的相互振动特性，按照一定的振动隔离原则对各系统进行模态分离，使其各自的固有模态频率尽量解耦，从而达到抑制或衰减振动的目的。

对于两个固有频率相互耦合的系统(见图3)来说，其运动微分方程为[14]：

(9)

对方程组(9)进行化简、求解，得到系统中各个设备的加速度传递率为：

R设备1=

(10)

R设备2=

(11)

图3 双自由度耦合系统

图4为取u=0.5，ξ1=ξ2=0.05，f=1时的系统设备的振动特性。只要设备的固有频率耦合，不论是刚性连接还是弹性连接，系统都会出现比较剧烈的共振，这也是进行模态规划的初衷。

4 模态匹配分析结果

采用以典型轨道车辆模态特性汇总结果为基础，以铁道客车的车体为模态匹配中心，以与之相连的系统为基本控制单元，以车辆平稳性指标及动态特性为依据的车辆模态匹配策略。

4.1 车体一阶弹性频率对平稳性的影响

对车体的一阶弹性模态进行改变，是通过调整车体主要结构的材料属性参数而达到，如改变边梁、枕梁、横梁等结构的弹性模量，具体见表1。当调整车体一阶弹性模态频率后，在美国5级线路谱激扰作用下，该型铁道客车在整备状态下以不同速度在直线上运行时，计算了车体一阶弹性体频率、构架浮沉频率及车体横向、垂向平稳性指标的变化情况，见表2和图5所示。

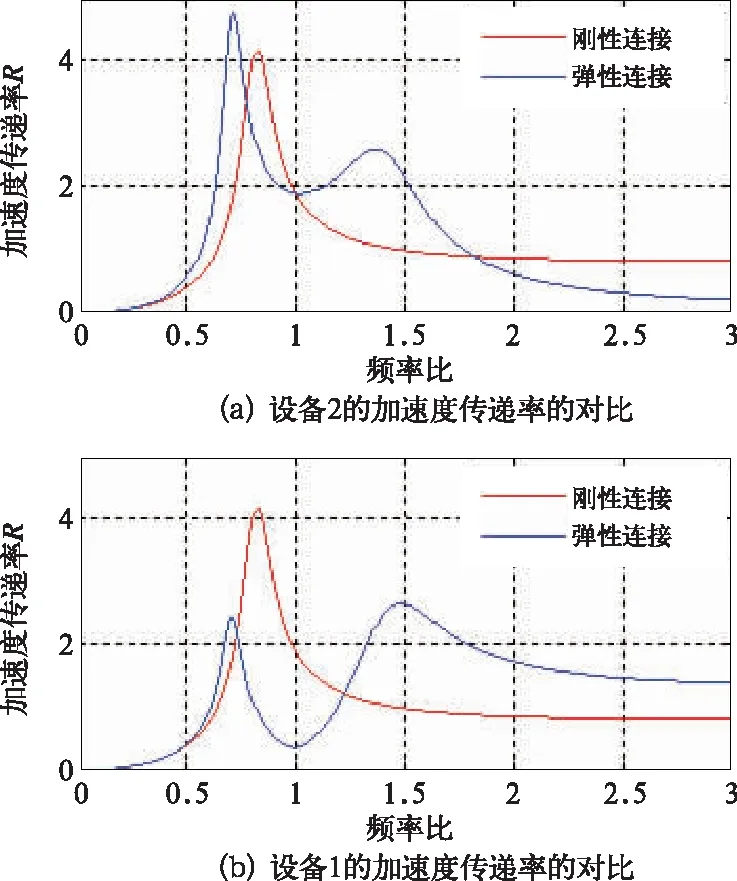
图4 固有频率耦合设备的振动传递率

当仅调整车体主要结构间的材料属性时，车体的刚体频率及构架的浮沉频率基本保持不变；整备车体的一阶弹性体模态都有所变化，一阶呼吸(车体的左右侧墙、底架及顶棚同步向内向外弯曲，简称为一阶呼吸模态)、一阶垂弯及一阶横弯的变化幅度较大，一阶垂弯频率变化范围为7.76～11.43 Hz。

在工况1和工况2时，车体中间测点的横向平稳性指标在某些速度级下无法满足GB/T 5599—1985[14]规定的新造客车2级良好标准。车体前、后测点的横向平稳性指标及前、中、后测点的垂向平稳性指标虽然在计算的速度级范围内能够满足GB/T 5599—1985规定的新造客车1级优秀标准，但是随着速度的增加，平稳性指标恶化趋势较为明显。

表1 各工况下材料弹性模量的取值

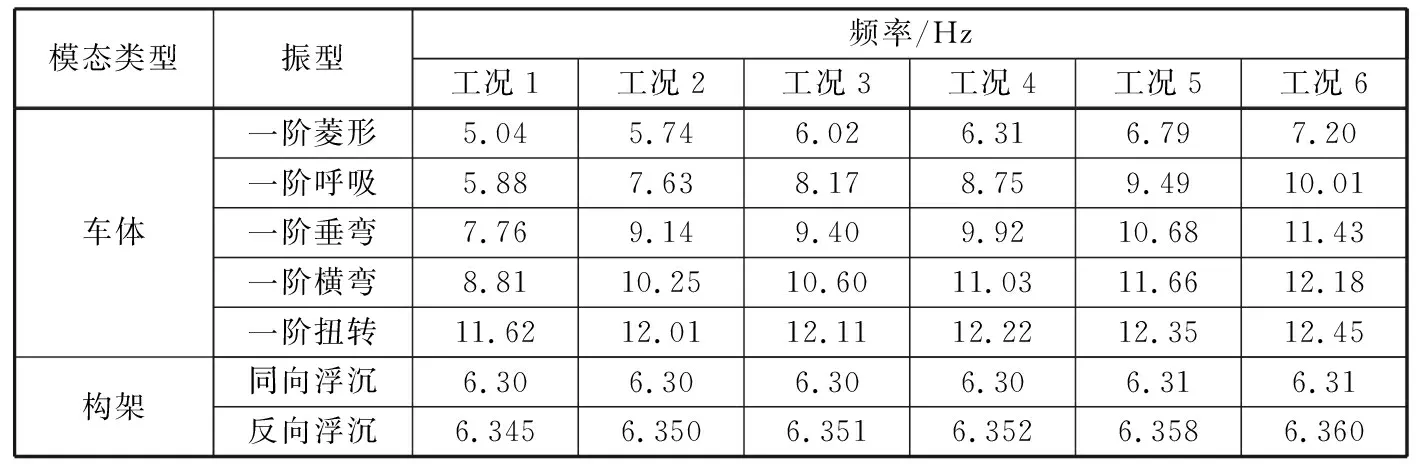
表2 各工况下模态频率对比

在工况3和工况4时，车体前、中、后测点的横向及垂向平稳性指标随着速度的增加会有较快的上升，特别是速度大于140 km/h时上升趋势比较明显，但上升幅度比工况1和工况2要慢，车体中部测点的横向平稳性变化最为明显，某些速度级下中间测点的横向平稳性指标达到GB/T 5599—1985规定的新造客车2级良好标准。

在工况5和工况6时，车辆前、中、后测点的横向及垂向平稳性指标随着速度的增加会有一定地上升，但是上升趋势趋于缓慢，上升量较小，且都满足GB/T 5599—1985规定的新造客车1级优秀标准。

4.2 各一阶弹性模态对平稳性的贡献度分析

为了分析车体典型一阶弹性模态(一阶垂弯、一阶呼吸、一阶菱形、一阶横弯、一阶扭转)在车辆平稳性中的贡献量，在不改动车辆参数的情况下，以4.1节的工况4模型为例，对仅考虑一阶垂弯、一阶呼吸、一阶菱形、同时考虑以上前3阶模态、一阶横弯、一阶扭转、考虑全部模态的7种工况下的车辆进行动力学计算，分析其横向、垂向平稳性指标变化，结果见图6所示。

对于车体端部的横向平稳性，车体各弹性模态对其影响均较小，其中一阶菱形模态影响相对较大；对于车体中部横向平稳性，车体一阶菱形模态影响较大，一阶横弯存在一定影响，其他模态对其几乎没有影响；对于车体端部垂向平稳性，车体低阶整体模态对其影响均较小，一阶菱形模态影响相对较大；车体高阶弹性模态对其有较大影响；对于车体中部垂向平稳性，车体一阶呼吸和一阶垂弯存在一定影响，其他一阶弹性模态影响不大；车体局部弹性模态对其有较大影响。

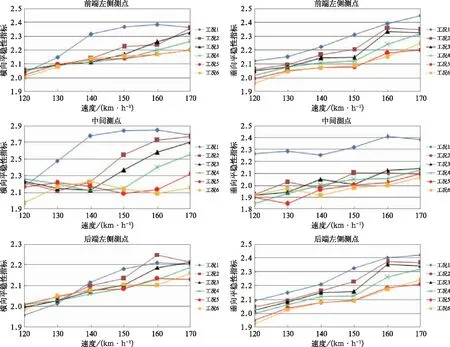
图5 车体地板面不同测点的平稳性指标

图6 不同模态参与贡献的车辆平稳性

4.3 关键部件的模态匹配分析

车体是振动传递的通道和振动最终的接受体，各种振动都会通过车体传入车内，振动在车辆的部件设备与车体之间相互传递。按照振动隔离原则，在模态规划中，车体结构或各个部件之间应尽量遵守1.4倍隔离，但由于车辆实际结构的限制，各个部件的主要模态范围是一定的，难以将所有部件理想化隔离，因此对无法按照理想隔离原则错开频率的部件，相互之间可取间隔2～3 Hz，并以满足车体平稳性指标为首要原则。表3给出了该型铁道客车整备车体比较关注的部分弹性模态。

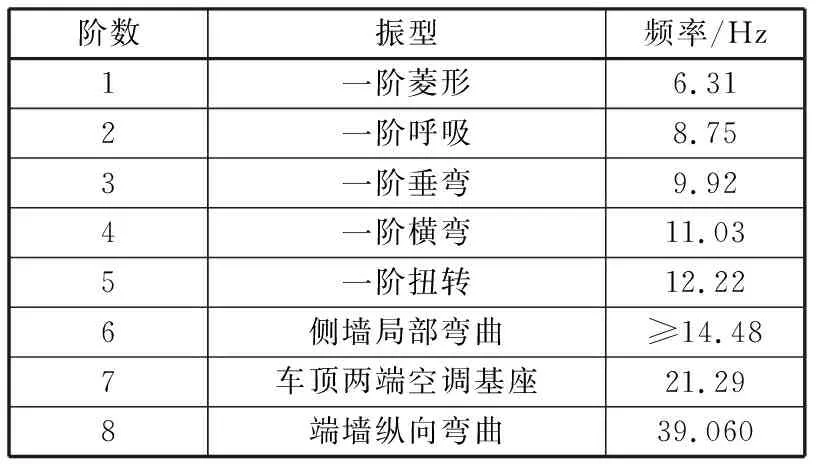
表3 整备车体部分低阶弹性模态

该型铁道客车最高设计运行速度为160 km/h，车轮直径915 mm，车轮转频15.46 Hz。由于轮对不可避免的存在动不平衡，因此将对车体振动产生贡献。为了降低该振动，也应对车辆设计速度下的车轮转频与车体主要垂向模态进行有效隔离。

该型铁道客车安装的空调机组的压缩机转速为2 900 r/min(基频48.33 Hz)，离心风机转速为1 420 r/min(基频23.67 Hz)，轴流风机转速为1 340 r/min(基频22.33 Hz)。经试验研究发现，轴流风机是该空调的主要激励源，因此认为空调机组对车体的主要激励频率为22.33 Hz。

以运行速度160 km/h为例，给出了4个主要的车下吊挂设备(无源)安装位置对应地板点的垂向幅频特性曲线，并据此给出吊挂设备附近区域的较大振动响应的频率范围。

从图7中看出，在车辆运行工况下，4个车下吊挂设备安装位置对应地板点均主要在6.14 Hz、10.19 Hz、14.17～22.74 Hz处有较大的振动响应。基于模态匹配原则，并借鉴以往车辆设计经验，车下吊挂设备本身的固有频率一般认为达到25 Hz以上即可。

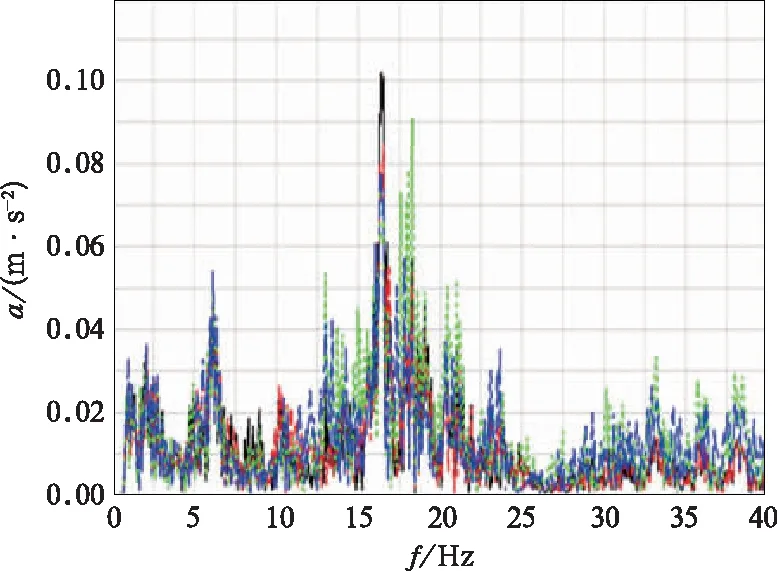
图7 车下4个主要吊挂设备附近地板的垂向响应

图8和图9分别给出了车体左、右侧墙顶部靠近行李架区域的前、中、后测点的横向、垂向振动响应特性曲线。车辆运行工况下，无论是横向还是垂向，左、右侧墙顶部行李架区域前中后测点均主要在6.17 Hz、13.92～24.50 Hz、30.16～39.93 Hz处有较大的振动响应。按照以往车辆设计经验[15]，侧墙顶部变形对行李架影响较大，而车体的一阶扭转(12.22 Hz)是影响侧墙顶部变形的主要模态振型，按照隔振理论，行李架的固有频率至少为17.28Hz。同时结合图7振动响应结果和空调机组的激励频率范围，行李架的固有频率范围可推荐在26～27 Hz之间。

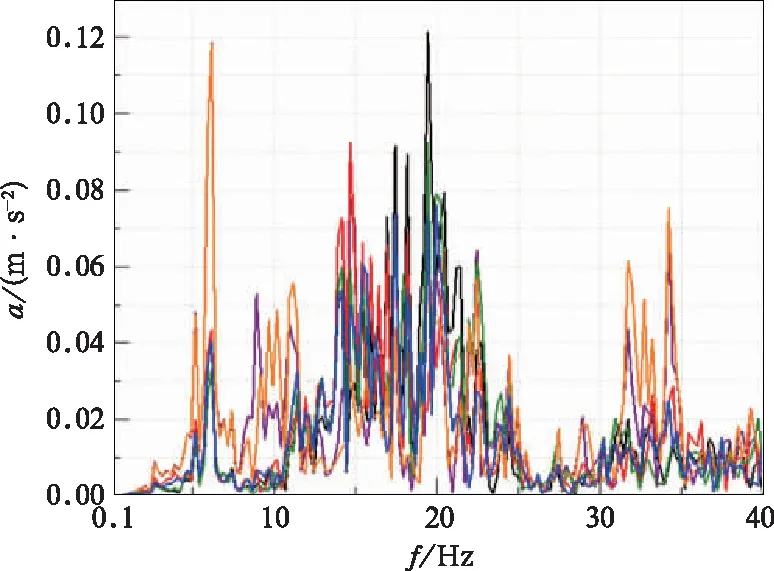
图8 侧墙顶部行李架区域前中后点横向响应

结合以上分析，以该型铁道客车为例，初步规划出了其车体、转向架构架、侧窗玻璃、行李架、车顶空调区域、吊挂设备、端墙模态频率推荐范围，见表4。

图9 侧墙顶部行李架区域前中后点垂向响应

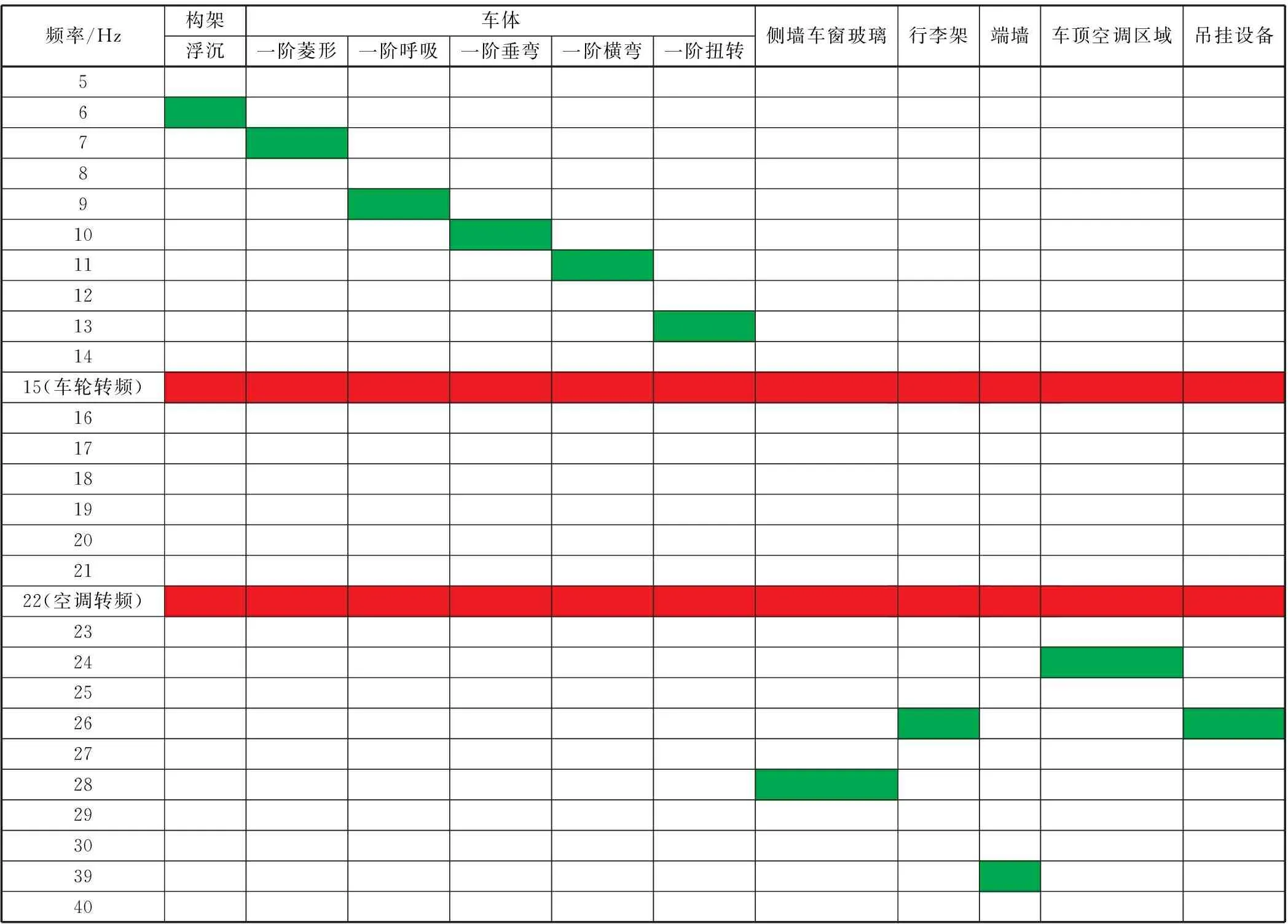
表4 某铁道客车系统的模态推荐表

5 结 论

(1)通过分析车体弹性模态变化取值、单独关键模态对车辆运行平稳性的影响和车体局部结构、附属设备等的动态响应特性，对某典型铁道客车进行了车辆系统的模态匹配研究，并据此给出了铁道客车关键系统模态频率推荐表。

(2)借鉴同样的分析方法，也可进行铁道客车其他车型的模态规划研究，如座车、卧铺车、餐车等，还可以根据车辆主体结构所用材料给出适用于不同材料车辆的模态规划推荐表。

(3)主要以车辆运行平稳性和局部的动态响应为分析目标，没有考虑对车辆稳定性指标的影响，在模态规划的后续深入研究中可更全面分析各模态特征对车辆性能的影响，对该方法以更好的完善和拓展。