高速磁浮车辆通过小半径竖曲线时的动力学响应分析*

梁 鑫， 赵春发， 罗英昆, 虞大联

(1 中车青岛四方机车车辆股份有限公司， 山东青岛 266111；2 西南交通大学 牵引动力国家重点实验室， 成都 610031)

为了实现高速磁浮列车600 km/h的运营速度目标，减小磁浮车辆走行部自重，同时确保磁浮列车具有良好的乘坐舒适性能，提出了一种基于德国TR09磁浮车辆系统的改进型悬浮架方案。该创新悬浮架取消了TR09车辆悬浮架的摇枕和吊杆结构，将空气弹簧直接布置在悬浮架两端的横梁上，从而简化了悬浮架结构，但对空气弹簧的伸缩变形提出了更高的要求。作为车辆二系悬挂系统的重要部件，空气弹簧具有复杂的结构和很强的非线性特性，而合理的空气弹簧技术参数选取首先需要了解其荷载条件和几何约束边界。因此，在空气弹簧方案选型和参数设计早期阶段，一般需要建立车辆系统动力学模型，仿真分析获得不同工况条件下车辆空气弹簧的运动学和动力学特性。

早期的轨道车辆二系空气弹簧设计中很少开展车辆系统动力学分析，一般仅采用有限元方法对空气弹簧气囊结构进行静力学分析。近年来，随着空气弹簧在轨道交通车辆中的广泛应用，国内外学者针对空气弹簧模型已开展了大量的研究工作。Berg定义了空气弹簧三维模型[1]，并且考虑了其内部空气的共振。Quaglia、Nieto和Docquier等根据流体力学和热动力学方程对橡胶气囊和空气室分别进行建模[2-6]，但没有考虑橡胶气囊与附加空气室之间的管路和节流孔对空气运动的影响。Oda等利用“弹性支撑阻尼”系统建立了适用于更宽频域范围的空气弹簧模型[7-10]，该模型没有考虑空气在管路中的惯性效应。石军等建立了中低速磁浮列车采用的约束膜式空气弹簧有限元模型，分析了空气弹簧的承载力和各向刚度特性[11-14]。在北京八达岭旅游示范线磁浮列车研制中，尹力明和赵志苏开展了空气弹簧高度阀安装位置及气囊连接方式的多方案试验和比较[15]，提出了空气弹簧及减振器参数选取的原则。高定刚等采用有限元法分析了磁浮列车用自由膜式空气弹簧的垂向刚度特性，给出了帘线角、内压力等对空气弹簧的影响规律[16-17]。由上可见，已有研究主要集中在空气弹簧自身力学性能的分析，在车辆系统动力学模型中大多采用了等效线性弹簧-阻尼器模型，很少有文献建立了考虑完整的空气弹簧非线性模型的车辆系统动力学模型，用于研究非线性空气弹簧的动力特性及其对车辆动力性能的影响。

分别建立了考虑等效线性化空气弹簧、复杂结构非线性空气弹簧的高速磁浮车辆系统动力学模型，采用Simpack软件仿真计算了磁浮车辆通过小半径竖曲线时的动力学响应，对比分析了两种空气弹簧模型对磁浮车辆动力学响应计算结果的影响，研究结果为新型高速磁浮车辆二系空气弹簧结构设计与参数选取提供了参考。

1 空气弹簧模型

在现有的轨道交通车辆动力学仿真分析中，大多数学者将空气弹簧简化为刚度阻尼并联的线性弹簧，弹簧的刚度由共同考虑空气弹簧橡胶气囊和附加气室等效计算获得，阻尼由节流孔阻尼效应等效计算得到，等效线性化空气弹簧模型如图1所示。图中，k是空气弹簧的垂向等效刚度；c是空气弹簧的垂向等效阻尼；X(t)是空气弹簧工作时的外部激励。但是，实际上空气弹簧系统一般由橡胶气囊、高度调整阀、应急橡胶堆、附加气室、供风风缸和节流孔组成，如图2所示。

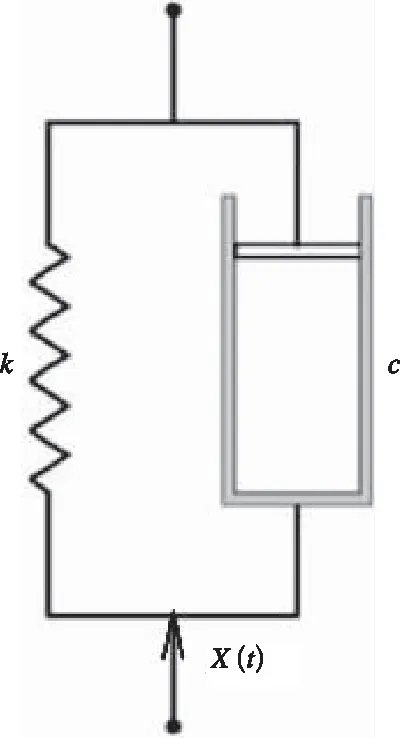
图1 空气弹簧等效模型

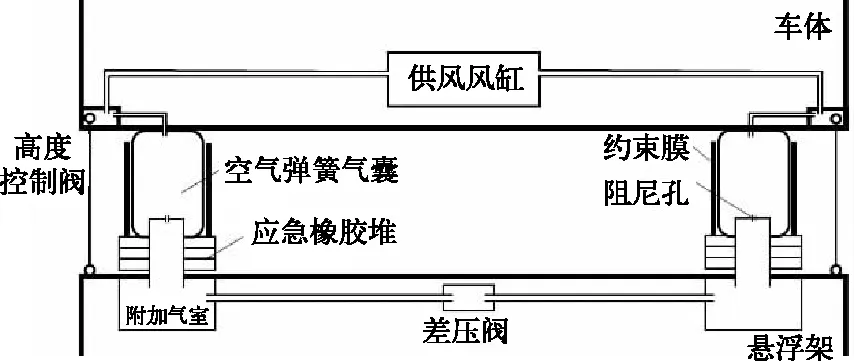
图2 空气弹簧结构示意图

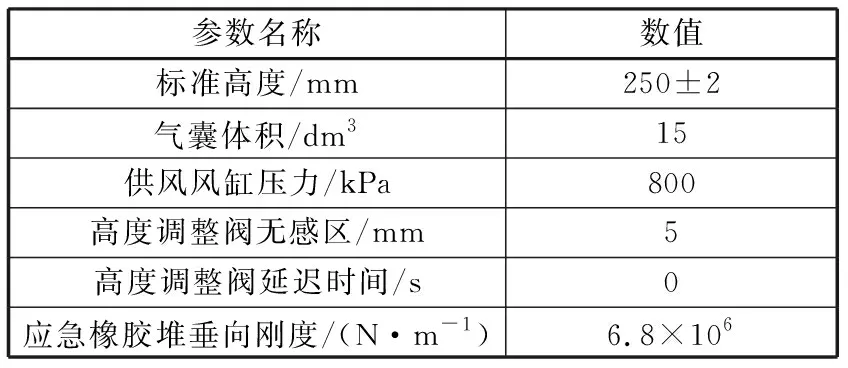
表1 空气弹簧基本参数

橡胶气囊内部封装一定量的空气，通过空气的流动性和可压缩性以及橡胶气囊的弹性达到垂向隔振的作用。高度调整阀安装在悬浮架和车体之间，其主要作用是控制供风风缸对气囊的充排气。高度调整阀有3个阀口，分别通过气动管路与供风风缸、外界大气和橡胶气囊相连。当空气弹簧的工作高度降低到一定值，通过高度调整杆作用使得阀芯移动，供风风缸阀口与橡胶气囊阀口连接，对空气弹簧充气；当其工作高度升高到一定值，橡胶气囊阀口与外界大气相连，使空气弹簧排气。应急橡胶堆安装在空气弹簧下盖板和底座之间，与上部气囊串联。其主要作用是保障空气弹簧失气后车体和构架不会发生刚性接触，同时在空气弹簧正常工作时，应急橡胶堆也能为空气弹簧提供一定的径向刚度以提高橡胶气囊的抗剪强度。附加气室经阻尼孔与橡胶气囊相连，从而增加了空气弹簧的气室体积，一定范围内可减小空气弹簧垂向刚度。节流孔的截面孔径很小，对流经的气体产生局部阻力及能量耗散，达到衰减车体振动的目的。表1所示为磁浮空气弹簧非线性模型的主要参数。

使用LMS公司的多学科复杂系统建模仿真平台AMESim，建立了高速磁浮车辆非线性空气弹簧动力学模型，如图3所示。

图3 非线性空气弹簧模型

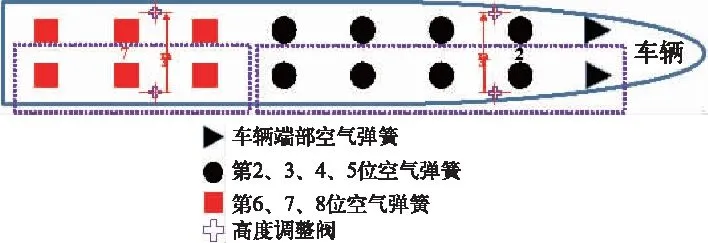
图4 单节车空气弹簧系统模型

图4给出了头车单侧空气弹簧模型以及支撑方式。单节磁浮车辆采用4个悬浮架单元，每个悬浮架上方布置4个空气弹簧支撑车体，每车共有16个空气弹簧。整车空气弹簧采用4点支撑方式，即单侧第1、2、3、4、5位空气弹簧为一组，第6、7、8位空气弹簧为一组。这种支撑方式不同于传统高速动车组的4点支撑。4个高度调整阀分别设置在第2、7位空气弹簧外侧的悬浮框上，左右间距3 m。每个高度调整阀控制一组空气弹簧，各组中的空气弹簧气囊进排气动作一致。高度调整阀采集到车体相对于悬浮架的垂向位移信号位于-5～5 mm之间时处于高度调整阀的无感区内，此时，进排气阀口都关闭，对应控制的气囊内气压值不变；当位移信号大于5 mm时，进气口阀门开，供风风缸对气囊充气，气压值增大；当位移信号小于-5 mm时，排气口阀门开，气囊排气，其内部气压值减小。

2 磁浮车辆动力学模型

采用SIMPACK软件建立了高速磁浮车辆动力学模型，如图5所示。高速磁浮车辆设有4个悬浮架单元，14块悬浮电磁铁和两个半体悬浮电磁铁。一个标准悬浮电磁铁模块包括两个半体悬浮电磁铁，每个半体悬浮电磁铁对应一套悬浮传感器和一套悬浮控制器。另外，每节车有14组导向电磁铁，对应28套导向控制系统。悬浮架结构中前、后两个C型框是悬浮/导向/制动电磁铁的安装基础，通过纵梁连接；空气弹簧连接车体和悬浮架，每个C型框上左右设置一套空气弹簧；左右导向电磁铁和悬浮电磁铁通过橡胶节点安装在C型框上，悬浮架之间通过搭接电磁铁相连。额定悬浮间隙和额定导向间隙均设置为10 mm，电磁铁与轨道面之间通过控制力元连接，将每个电磁铁12个磁极的电磁力简化为电磁铁首尾两个控制力。

图5 单节磁浮车辆动力学模型

图5模型中电磁悬浮/导向力计算公式为

(1)

式中，I是电磁铁线圈电流；N是线圈匝数；A为有效磁极面积；δ为悬浮间隙；μ0为空气磁导率。可见，电磁力和间隙的平方成反比，与线圈电流的平方成正比。

没有反馈控制的开环常导电磁悬浮系统是不稳定的，即使受到很小的外部干扰，系统都会失去平衡。为了实现稳定悬浮，必需进行主动反馈控制，文中采用了基于状态观测器的间隙、间隙速度和间隙加速度的反馈控制系统，其控制流程如图6所示。

悬浮控制器输出的控制电流可表示为式(2)

(2)

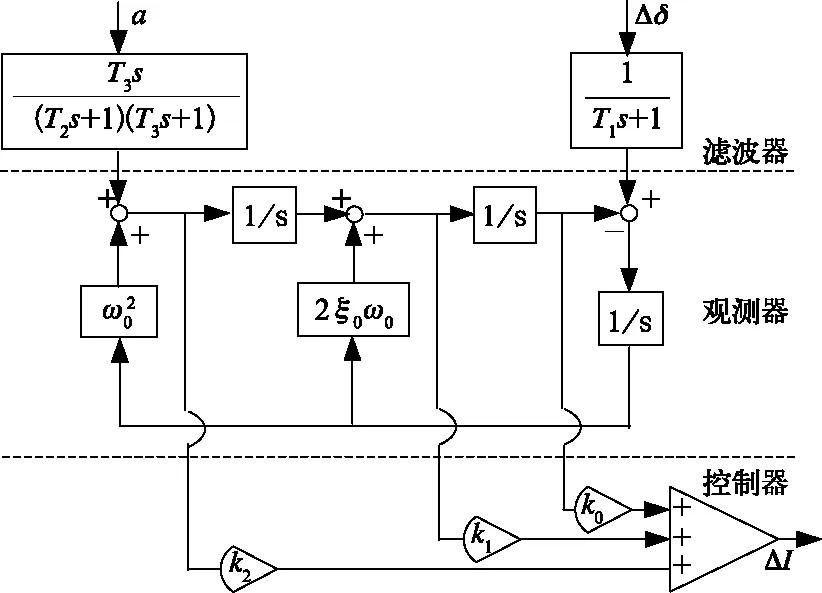
图6 悬浮控制系统流程图

3 数值模拟方法与计算工况

在分别建立图4所示精细化非线性空气弹簧模型和图5所示磁浮车辆动力学模型基础上，利用AMEsim软件和Simpack软件接口Functional Mock-up Interface，将车辆模型计算得到的空气弹簧伸缩量作为空气弹簧模型的输入，经AMEsim计算后得到空气弹簧垂向力，输入到Simpack车辆模型中，从而实现非线性空气弹簧系统与车辆刚体系统的耦合计算，如图7所示。另外，在Simulink中建立电磁悬浮/导向控制系统模型，选择合适的编译器，生成MATSIM模型文件；通过MATSIM接口调用MATSIM文件，实现悬浮/导向控制系统和车辆系统之间耦合计算。

基于等效线性化空气弹簧模型和非线性空气弹簧模型，计算高速磁浮车辆以30 km/h速度通过小半径竖曲线时的动力学响应。仿真计算时，单节车质量为48 664 kg。凸竖曲线参照上海高速磁浮示范线技术规范设置，竖曲线半径为530 m，仿真模型未考虑不平顺对空气弹簧的影响。如图8所示。

图7 Simpack和AMESim耦合计算示意图

图8 凸竖曲线纵剖面示意图

4 竖曲线上高速磁浮车辆动力学响应

4.1 车体和电磁铁动态响应

图9是新型高速磁浮车辆车体质心垂向位移响应曲线。比较等效线性空气弹簧和非线性空气弹簧的计算结果，可以发现，车体质心垂向位移响应曲线几乎重合，垂向位移最大值分别为40.26 mm和41.32 mm，计算误差仅为2.5%。位移峰值均对应于车辆通过竖曲线最高点时，磁浮车辆较好地跟踪了竖曲线纵坡坡度的变化。

图10和图11分别是车辆第1个悬浮架第2位悬浮控制点处的悬浮间隙与悬浮力响应曲线。结果表明，采用两种空气弹簧模型的计算结果曲线波形一致，幅值相当；悬浮间隙最大波动量均为1.1 mm，悬浮力最大波动量均为10.4 kN。图10和图11还表明，悬浮间隙增大时悬浮力也随之增大，很好地体现了电磁悬浮控制的基本原理。综合分析图9～图11结果可知，采用等效线性化空气弹簧可以获得较为准确的磁浮车辆车体振动响应、电磁铁振动响应计算结果。

图9 车体质心垂向位移

图10 第1个悬浮架第2位控制点悬浮间隙

4.2 空气弹簧动态响应

图12和图13分别给出了高速磁浮车辆通过凸曲线时等效线性化空气弹簧和非线性空气弹簧的动态伸缩量变化曲线。两种空气弹簧模型计算得到的空气弹簧伸缩量具有相同的变化规律，即通过凸曲线时车辆端部第1、2、7、8位空气弹簧拉伸，车辆中部第3、4、5、6位空气弹簧压缩，这是因为纵向分布的悬浮架和悬浮电磁铁较好地贴靠了竖曲线线形，不同位置空气弹簧垂向变形规律符合竖曲线上车辆底板与曲线轨道的相对位置关系。

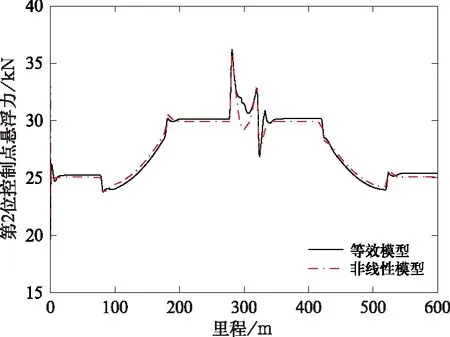
图11 第1个悬浮架第2位控制模块悬浮力

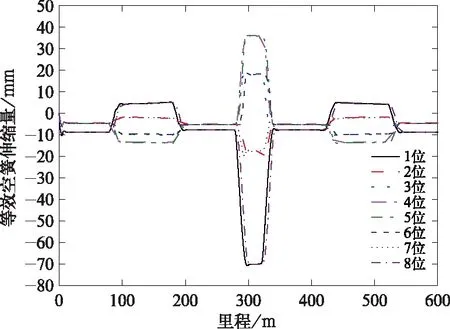
图12 等效模型空气弹簧伸缩量

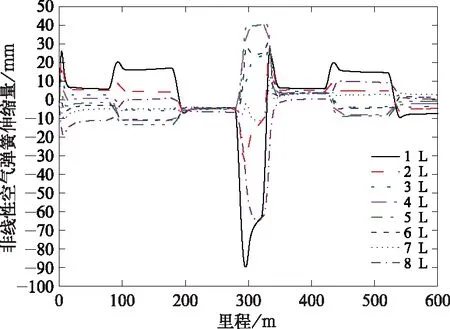
图13 非线性模型空气弹簧伸缩量

图14比较了等效线性化空气弹簧和非线性空气弹簧的伸缩量计算结果。可以看出，当车辆通过半径530 m 竖曲线时，同一位置处两种空气弹簧的伸缩量最大值有明显的差别；其中，第1位空气弹簧垂向最大拉伸量分别为70 mm和90 mm，两者差值最大，达到20 mm；如果以非线性空气弹簧的计算结果为准，则等效线性化弹簧模型的伸缩量计算误差达到29%。由此可见，当基于整车动力学模型预测分析二系空气弹簧的动态变形时，非常有必要采用非线性空气弹簧模型。

在新型车辆设计时，有必要在二系悬挂系统设置垂向止挡装置，限制空气弹簧垂向变形，并提供垂向辅助支承力，保护空气弹簧系统。

图14 两种模型空气弹簧伸缩量绝对值

5 结 论

建立了考虑橡胶气囊、高度调整阀、应急橡胶堆、供风风缸等部件的精细化空气弹簧非线性模型，以及考虑电磁悬浮控制的高速磁浮车辆动力学模型，仿真计算了一种新型高速磁浮车辆通过530 m小半径竖曲线时的动力学响应，并与采用等效线性化空气弹簧模型的计算结果进行了对比分析，得到以下结论。

(1) 分别采用等效线性化空气弹簧模型和非线性空气弹簧模型，磁浮车辆车体振动加速度、电磁铁间隙、电磁悬浮力等响应值差别不大，相对误差在3%以内。因此，如果仅仅预测评估高速磁浮车辆乘坐舒适度时，磁浮车辆动力学模型采用等效线性化空气弹簧模型是合适的。

(2) 采用等效线性化空气弹簧模型计算得到的空气弹簧变形量与非线性空气弹簧模型的计算结果有很大的差别，在本文计算条件下两种空气弹簧动态变形量最大相对误差达到29%。因此，在磁浮车辆二系空气弹簧结构与参数设计时，应采用非线性空气弹簧模型的车辆系统动力学模型进行分析与优化。

(3) 采用非线性空气弹簧模型的动力学计算结果表明，小半径竖曲线上无摇振悬浮架使得空气弹簧最大拉伸量达到70 mm，最大压缩量接近40 mm，这对二系空气弹簧结构设计提出了较高的要求，需要设置竖向止档对空气弹簧垂向变形进行限制。