方形容器设计计算分析比较

张焱，马斓擎，金东杰，张荻，金刚

（中核能源科技有限公司， 北京 100193）

工程上经常见到方形容器或方形接管，由于其结构简单、紧凑，制造方便，平稳性好，还有较大的表面积和较高的传热效率，常被应用在化工容器中，如各种洗槽、电镀槽、锅炉联箱以及分离器入口接管等。以一台分离器蒸汽进口方形接管为例，采用应力分析方法验证GB/T 150附录A计算方法的适用性。

1 设计参数

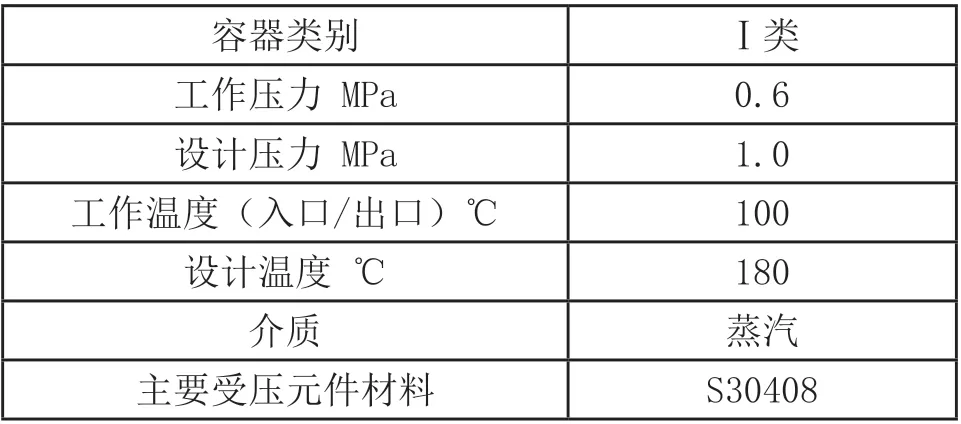
表1 分离器参数表

注：1.风载荷、地震载荷、重力载荷及设备内液柱静压头（气体，无静压头）产生的应力与设备内压产生的应力相比较小，对设备影响很小，因此不考虑风载荷、地震载荷、重力载荷及设备内液柱静压头的影响。

2.在正常操作情况下，容器设置了有效的保温，内外壁温差小，温度梯度也很小，温差应力对本设备强度和疲劳影响较小，故忽略热载荷相关计算。

3.在计算包括二次应力强度的组合应力强度时，应选用工作载荷进行计算。本报告中选用设计载荷进行强度分析结果是偏安全的。

表2 材料性能参数

2 方形接管截面形式

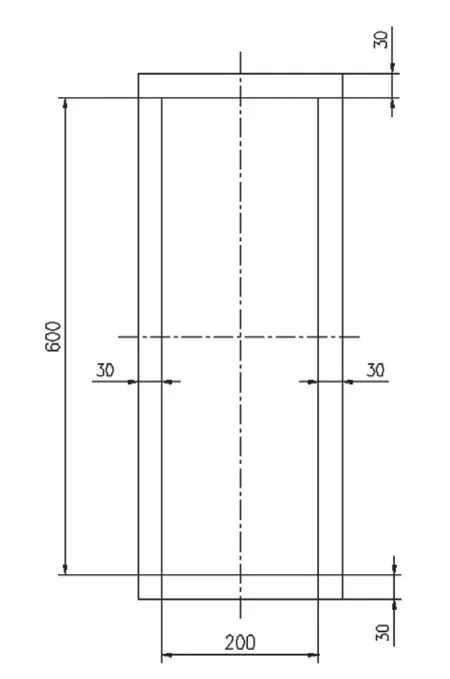
图1 分离器方形接管截面形式

3 结构分析

GB/T 150.3附录A对于非圆形截面容器给出了设计计算方法。分离器蒸汽进口方管可以看作无加强对称矩形截面容器，根据GB/T 150.3附录A进行计算。因为蒸汽进口方管两端分别与设备筒体和天圆地方接管相连接，不同于方形容器，有封头的加强作用，因此不能考虑封头加强作用的的修正系数。故将该方形接管看作纵横比大于4的方形容器，对其进行有限元分析，与GB/T 150.3附录A计算结果相对比，验证公式计算的符合性。

4 分析计算

4.1 用有限元法对分离器蒸汽进口方形接管进行分析

4.1.1 有限元分析模型

以方形接管轴线为Z轴，建立直角坐标系。仅分析方管部位，方管长度取600mm，但在方管两端面加对称约束，因此相当于有足够的轴向长度。建立设备的有限元模型如图2所示。为获取准确的应力分布情况，模型为三维实体模型。为方便建模和求解，对有限元模型进行了简化处理，忽略流体自身重力等对应力分布的影响。结构分析采用20节点六面体等参单元SOLID186进行网格划分。

图2 模型与网格

4.1.2 载荷及边界条件

计算载荷作用下的受力情况，在方管内壁施加内压载荷，对方管两端面施加对称约束，如图3所示。

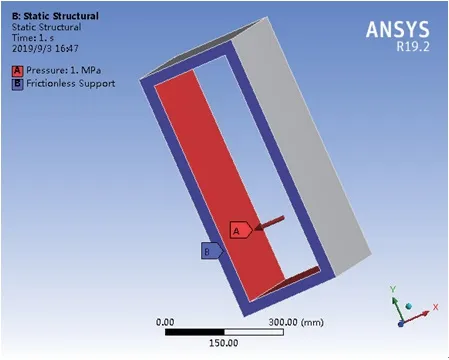
图3 载荷及边界条件

4.1.3 应力计算

分离器蒸汽进口方形接管应力分布如图4所示。从图4可以看出，由于在方管壁板转角位置发生了形状突变，应力水平偏大。长边中心处也是应力水平较大处。由有限元计算结果表明，最大应力出现在方形接管短边靠近角点内表面，其值为192.24MPa。

为进一步研究其应力分布，对各关键部位进行应力线性化。应力线性化路径的选择原则为：（1）通过应力强度最大节点，并沿壁厚方向的最短距离设定线性化路径；（2）对于相对高应力强度区，沿壁厚方向的最短距离设定线性化路径；（3）对于形状突变处，沿壁厚方向的最短距离设定线性化路径。

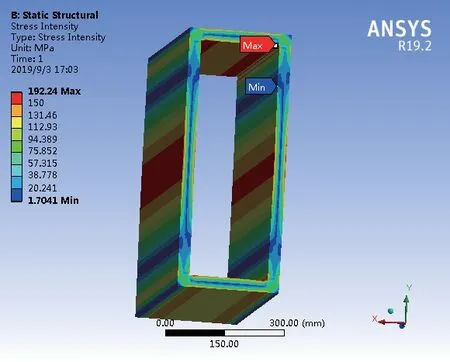
图4 应力分布

依据上述原则以及GB/T 150.3附录A，关于对称结构矩形截面容器计算方法，选择方形接管长边中点位置、短边中点位置及角点位置作为研究对象，还应选择应力最大点处为研究对象，分别取路径A～F，见图5。

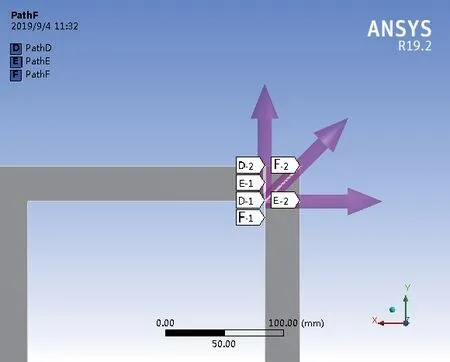
图5 应力线性化PathA～F

4.1.4 应力评定结果与分析按应力的性质、影响范围及分布状况将应力分为一次应力、二次应力和峰值应力。将薄膜应力归为Pm或Pl、弯曲应力归结为Pb，在结构不连续区或形状突变部位，弯曲应力存在一定二次应力成分，但为保守起见，故此部位薄膜应力加弯曲应力仍归为一次应力。

表3 方孔结构各路径应力强度评定表

4.2 GB/T 150.3附录A方法简述及用该方法对分离器蒸汽进口方形接管进行计算

4.2.1 GB/T 150.3附录A方法简述

目前非圆形截面容器的设计一般都采用试算法，即先根据以往使用的经验确定一个壁厚，再根据应力计算式和校核式进行强度校核，如果强度不够，就增加壁厚，直到满足强度条件。研究非圆形截面容器，关键是求壳体上的应力，GB/T150.3附录A求应力的基本方法采用了材料力学平面梁的假设。该方法假定壳体轴向长度为无限长，忽略了壳体两侧由于端盖的加强作用引起的应力变化；认为壳体上的应力沿轴向是均布的，且认为周向应力是第一主应力，不考虑轴向应力。按这种方法求得非圆形截面容器上的危险点为：矩形截面容器在角点或侧板中心。求出危险点的薄膜应力、弯曲应力及有关组合应力，然后分别按相应的强度条件进行应力校核。强度控制条件：采用类似于分析设计的方法，但不是采用弹塑性失效准则—以最大剪应力理论（第三强度理论）控制应力强度。它以最大主应力理论（第一强度理论）作为控制依据，同时考虑应力分类因素，但仅限于一次应力，即一次薄膜应力和一次弯曲应力，不考虑二次应力。该方法推导过程简单，计算方便，适宜工程计算，但局限性在于未考虑应力沿轴向的变化；计算的应力是单向的，未考虑轴向应力；认为壳体是无限长的，未考虑壳体两侧由于端盖的加强作用引起的应力变化，对轴向长度较短的壳体（纵横比＜4～5），计算结果偏保守。

4.2.2 按GB/T150.3附录A方法对分离器蒸汽进口方形接管进行计算

（1）结构

分离器蒸汽进口采用整体不锈钢锻件，没有焊缝。方形接管符合GB/T 150.3附录A中无加强对称矩形截面容器计算模型，方形接管的两对边侧板厚度相等，邻板厚度也相等，方形接管截面尺寸见图6。

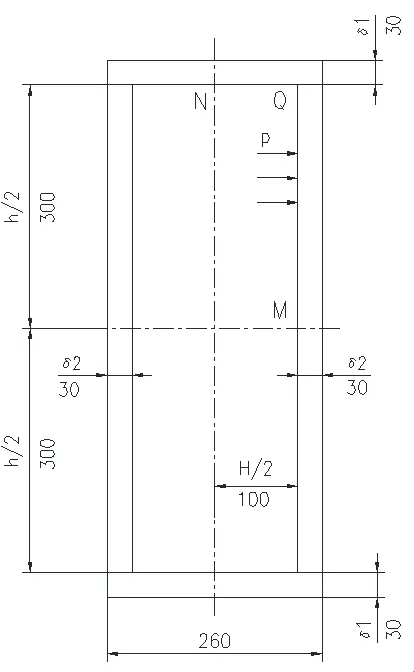
图6 方形接管截面尺寸

（2）符号

c -板截面中性轴至计算截面内表面的距离ci或至计算截面外表面的距离co。在对内外表面的弯曲应力计算中，应分别以ci或co代入，mm；H -矩形容器短边内侧长度，mm；h -矩形容器长边内侧长度，mm；I1、I2-短边侧板和长边侧板截面的惯性矩，mm4；I1=LS•δ13/12；I2=LS•δ23/12；K -参数，K=(I2/I1)α；α-参数，α=H/h；Ls-加强件起加强作用的有效宽度，对非加强容器取1，mm；Pc-计算压力，MPa；δ1-容器短边侧板的有效厚度，mm；δ2-容器长边侧板的有效厚度，mm；σb-弯曲应力，MPa；σm-薄膜应力，MPa；σT-总应力，MPa；[σb]t-设计温度下材料的许用应力，MPa；φ -焊接接头系数。

（3）应力计算

（a）短边侧板

侧板上N点和Q点的薄膜应力：

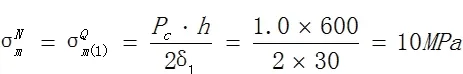
侧板内壁上N点和Q点的弯曲应力分别为：

其中：I1=LS•δ13/12=1×303/12=2250mm4，α = H / h = 2 0 0 / 6 0 0 = 0 . 3 3 3 3 ，I2=LS•δ23/12=1×303/12=2250mm4，K=(I2/I1)α=(2250/2250) ×0.3333=0.3333

侧板内壁上N点和Q点的总应力分别为：

侧板外壁上N点和Q点的弯曲应力分别为：

其中：I1=LS•δ13/12=1×303/12=2250mm4，α = H / h = 2 0 0 / 6 0 0 = 0 . 3 3 3 3 ，I2=LS•δ23/12=1×303/12=2250mm4，K=(I2/I1)α=(2250/2250) ×0.3333=0.3333

侧板内壁上N点和Q点的总应力分别为：

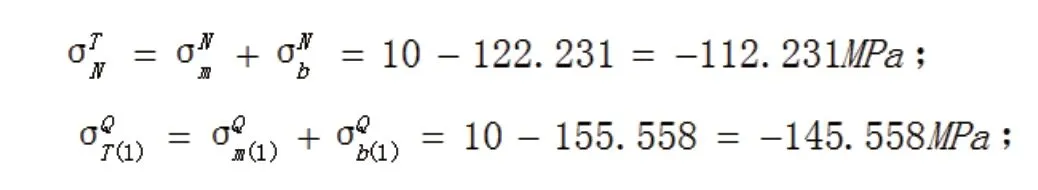
（b）长边侧板

侧板上M点和Q点的薄膜应力：

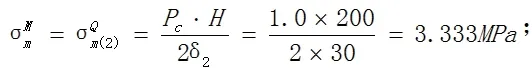
侧板内壁上M点和Q点的弯曲应力分别为：

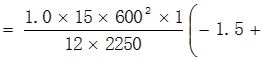
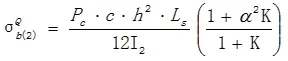
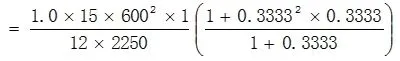
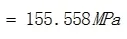
其中：I1=LS•δ13/12=1×303/12=2250mm4，α = H / h = 2 0 0 / 6 0 0 = 0 . 3 3 3 3 ，I2=LS•δ23/12=1×303/12=2250mm4，K=(I2/I1)α=(2250/2250) ×0.3333=0.3333

侧板内壁上M点和Q点的总应力分别为：

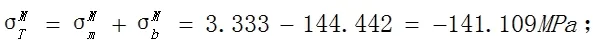
侧板外壁上M点和Q点的弯曲应力分别为：

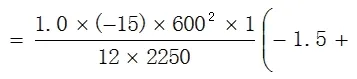
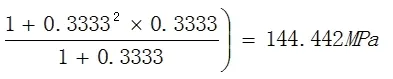
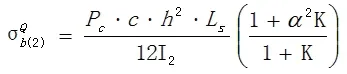
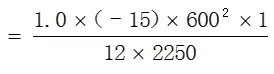
其中：I1=LS•δ13/12=1×303/12=2250mm4，α = H / h = 2 0 0 / 6 0 0 = 0 . 3 3 3 3 ，I2=LS•δ23/12=1×303/12=2250mm4，K=(I2/I1)α=(2250/2250) ×0.3333=0.3333

侧板外壁上M点和Q点的总应力分别为：

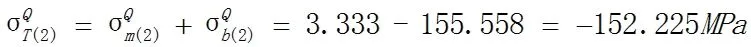
（4）应力校核

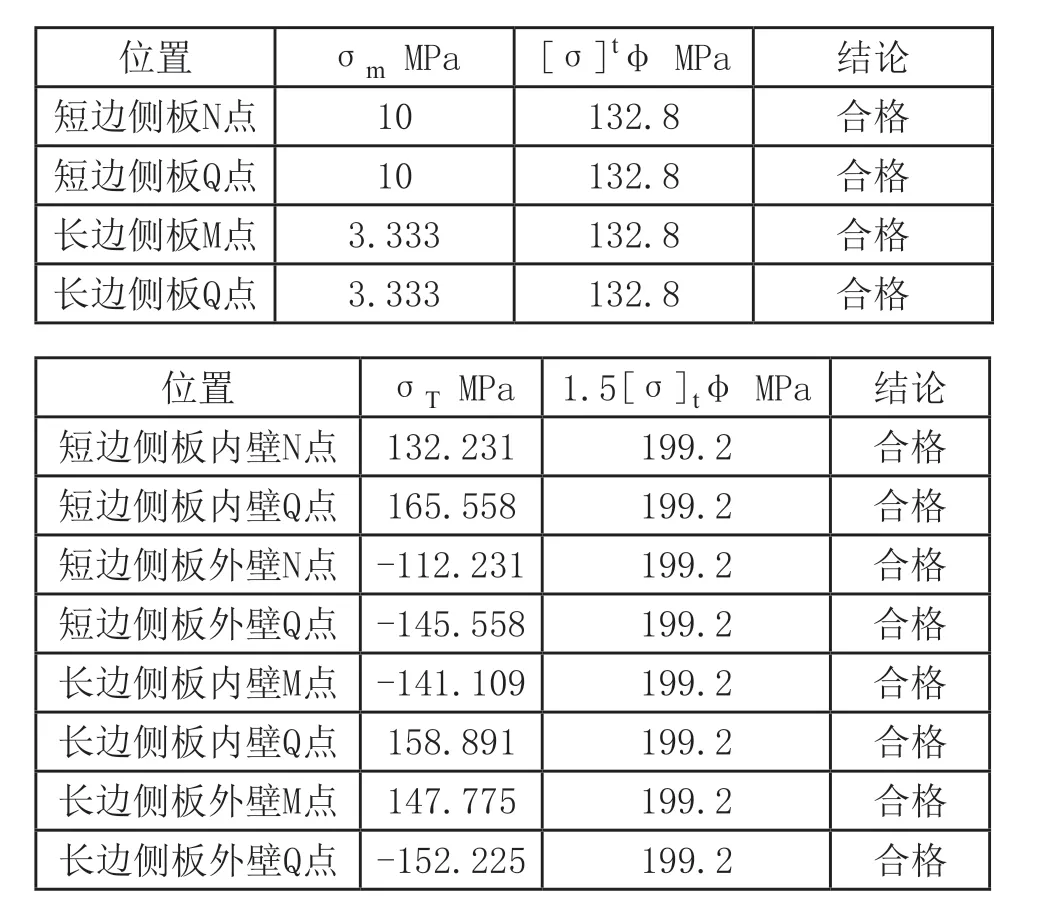
表3 应力校核结果

5 结论

采用有限元法和GB/T 150.3附录A的方法对方形接管进行计算，有限元法选取路径的位置与GB/T 150.3附录A中研究的位置一致，其计算结果对比见表4。

表4 有限元法与GB/T 150.3附录A法应力计算结果对比

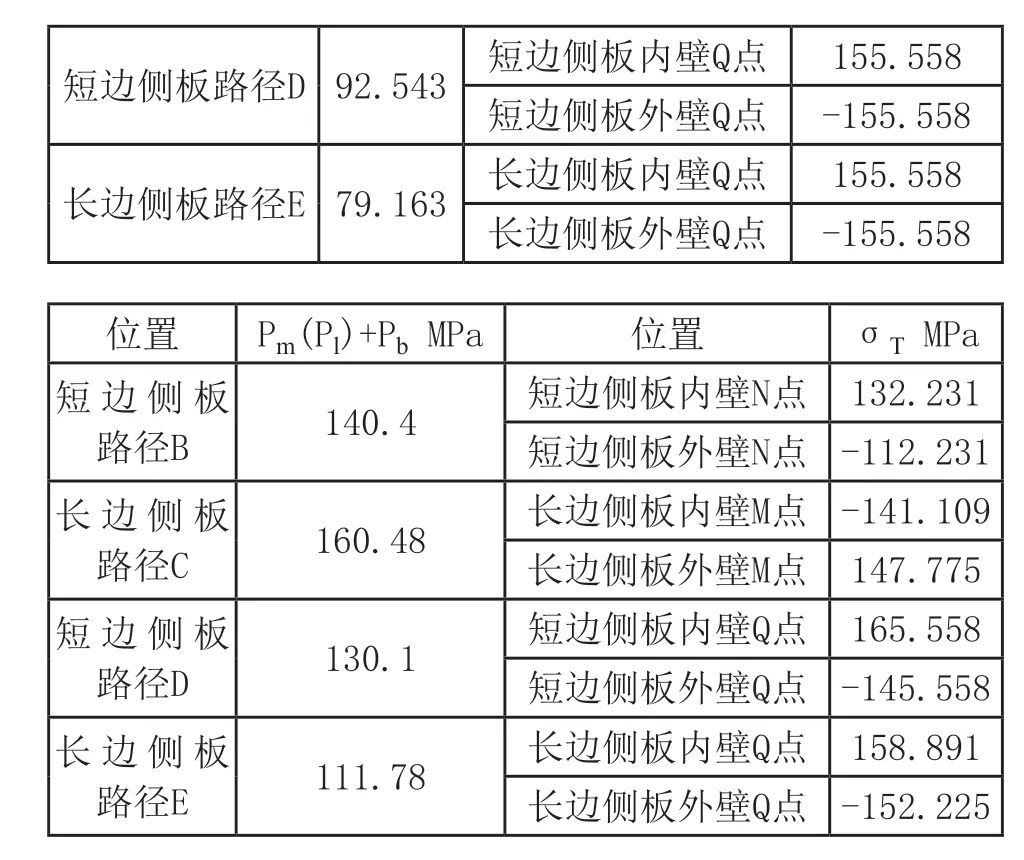
短边侧板路径D 92.543 短边侧板内壁Q点 155.558短边侧板外壁Q点 -155.558长边侧板路径E 79.163 长边侧板内壁Q点 155.558长边侧板外壁Q点 -155.558位置 Pm(Pl)+Pb MPa 位置 σT MPa短边侧板路径B 140.4 短边侧板内壁N点 132.231短边侧板外壁N点 -112.231长边侧板路径C 160.48 长边侧板内壁M点 -141.109长边侧板外壁M点 147.775短边侧板路径D 130.1 短边侧板内壁Q点 165.558短边侧板外壁Q点 -145.558长边侧板路径E 111.78 长边侧板内壁Q点 158.891长边侧板外壁Q点 -152.225

对计算结果和数据进行对比分析：

（1）由分析计算方法得出的长边与短边中心点处总体薄膜应力与GB/T 150.3附录A中公式计算的同位置的薄膜应力相当。

（2）在方形容器的角点，由于结构不连续，在压力作用下受变形协调的影响，分析得出的实际局部薄膜应力较大，但根据JB/T 4732，此处应力校核应采用1.5KSm作为评定的强度极限。而GB/T 150.3附录A中角点处薄膜应力采用与长、短边中心处薄膜应力同样的计算公式，计算出的是总体薄膜应力，以[σ]tφ作为评定的强度条件。

（3）短边侧板和长边侧板在压力作用下，其中点位置会产生较大的弯曲应力。中点处由分析计算得到的弯曲应力值较GB/T 150.3附录A公式计算得到的弯曲应力值偏大。这说明用GB/T 150.3附录A公式计算方形容器壁板中间位置的弯曲应力时结果偏小。

（4）角点处在压力作用下，受变形协调影响，弯曲应力有一定的二次成分。但分析计算得到的角点处的弯曲应力较GB/T 150.3附录A公式计算得到的角点处弯曲应力值小很多。虽然公式考虑此处的二次应力成分，但从结果看，对于角点位置，公式计算是偏保守的。

（5）由于用GB/T 150.3附录A公式计算方形容器壁板中间位置的弯曲应力时结果偏小，因此用于强度校核的总应力—薄膜应力+弯曲应力在该位置的计算值也较分析计算得到膜加弯的实际值偏小。如果方形容器根据公式计算所得的总应力按照强度条件评定刚好合格时，方形容器可能是不安全的。

（6）从应力分析结果可以看出，长边中心处为高应力区，与GB/T 150.3附录A研究的危险位置相符；但分析结果显示，短边的高应力区并不在短边中心，由于短边尺寸较短，中心处弯曲应力水平不高，高应力区位于靠近转角处，却不在转角处，这与GB/T 150.3附录A研究的危险位置不相符。这说明GB/T 150.3附录A不考虑截面尺寸和壁板厚度等情况，把危险点设定在壁板中心处和角点处是不合理的。

◆参考文献

[1] GB/T 150.3-2011，压力容器 第3部分 设计[S].

[2] JB/T 4732-1995，钢制压力容器—分析设计标准（2005年确认）[S].

[3] 全国锅炉压力容器标准化技术委员会. 压力容器设计工程师培训教程[M].北京：新华出版社，2005.

[4] 高红利，洪锡纲. 非圆形截面容器的特点及其应力计算[J].暨南大学学报（自然科学版）2003，24(1)：87-89.

[5] 曹国防. 超范围非圆形截面容器的设计计算[J].石化技术，2000，7(1)：25-28.