再入气动环境类电池帆板材料微观响应变形行为分子动力学模拟研究

孙学舟，李志辉，2*，吴俊林，马 强

（1.中国空气动力研究与发展中心超高速空气动力研究所，绵阳621000；2.国家计算流体力学实验室，北京100191；3.四川大学数学学院，成都610043）

1 引言

运行在低地球轨道环境的板舱桁架式大型航天器在其服役期满终将面临离轨再入大气层解体坠毁的问题［1-2］，因此需要分析评估其对覆盖空域的人、财、物及生态系统的危害性。该类航天器再入过程经历高超声速气动力/热坏境［3-4］，会在复杂气动力热载荷作用积累下发生软化熔融解体［5-6］。准确分析这些航天器的再入解体损毁，对可靠预报航天器再入解体残骸碎片落区，提前做好处置准备工作，将可能的人员伤亡与财物损失风险降至最低等意义重大；而进一步的解体损毁设计则可在确保航天器正常性能的前提下，力争实现再入过程结构的充分解体烧蚀，减少乃至回避坠落地表的航天器解体残留物造成的危害。

为实现服役期满航天器再入过程结构解体坠毁可靠数值预报，需要将跨流域高超声速的气动力热分析同材料结构的实时变形与破坏分析相耦合［4，7-8］。对于跨流域高超声速的气动力热流场计算，李志辉等［9-11］建立了从稀薄流到连续流求解Boltzmann模型方程气体动理论统一算法（GKUA），给出了精确进行跨流域高超声速流场计算的方法；彭傲平等［12-13］对GKUA方法进行了发展，实现了对飞行器物面不同位置力、热流、温度、速度分布等绕流环境的准确捕捉；马强等［6，14-15］则基于经典傅里叶导热定律，建立了高超声速气动坏境致结构动态热力响应变形行为的有限元算法，初步实现了将流场计算同结构变形有限元计算分析的耦合。但这一体系中针对材料在复杂力/热坏境下的毁坏分析采用的是基于准静态模型建立的经典材料强度理论分析方法，在航天器再入这样的极端载荷条件下尚显不足，而分子动力学模拟方法针对材料微观尺度的位移及加热效应对材料力学性能变化与破坏失效分析，预期可进一步模拟揭示其微观响应行为。

本文针对二组元合金——碳元素质量分数为0.215%的含碳钢这一类桁架结构大型航天器电池帆板简化模型平板材料，应用分子动力学模拟其在高超声速再入气动环境力/热载荷作用下的微观力学行为，分析材料在再入气动环境不同温度条件下的力学性能，研究材料在高温条件下微观缺陷萌发演化、弹塑性失效过程微观缺陷萌发演化、弹塑性失效过程，以期为更加准确可靠地通过动态热力响应有限元算法对服役期满航天器再入强气动力热环境致金属合金材料结构变形失效熔融毁坏过程模拟奠定基础。

2 含碳钢材料模型的建立与验证

2.1 分子动力学模型的基本晶格模型

本文模拟时所建立的含碳钢材料的分子动力学仿真模型均是基于具有体心立方晶格（bcc）结构的α-Fe金属构建，图1展示了具有体心立方晶格结构的晶胞示意图。

图1 体心立方晶格结构示意图Fig.1 The crystal structure of body-centered cubic unit cell

图中，立方体晶胞的边长a一般称为晶格常数，在晶体结构的固体材料中，平衡状态下的晶格常数a跟随温度T的变化规律近似满足宏观材料实验中得出的线膨胀规律，若将不同温度下材料的平衡态晶格常数与温度进行线性拟合得其斜率k，则可由式（1）计算得出材料的线膨胀系数α。

2.2 原子间作用势

在分子动力学模拟中，用来描述模型内部粒子相互作用的原子间作用势函数的选用是否合理，对模拟结果是否准确影响较大。根据Rajabpoura等［16］针对单晶铁和含碳钢的体模量的平衡态分子动力学计算中不同势函数的分析，对于含碳钢体系，选取MEAM势和Tersoff势较为合理。本文工作中的分子动力学模拟均采用Liyanage等［17］在2014年提出的MEAM势函数。所选取的势函数的系统总能量如式（2）。

2.3 含碳钢材料分子动力学模型的建立

参照Rajabpoura等［16］构造合金钢仿真模型的方法，基于α-Fe金属晶格结构，构造Fe、C原子数量比99∶1（C元素质量分数0.215%）的bcc含碳钢材料MD模型，具体构建方法如下：

1）根据模拟所需的晶胞数量，以bcc模型构建对应尺寸的单晶α-Fe，并将这一体系在NVT系综下进行弛豫，使模型达到平衡；

2）随机将模型中1%的Fe原子替换为C原子，并用选定的MEAM势函数描述模型中原子间相互作用，在NVT系综下充分进行能量最低弛豫，使模型达到平衡，得到含碳钢MD模拟模型。

2.4 模型与势函数的验证

在300～1000 K的不同温度下，建立一系列原子数量为500的小规模材料模型，采用所选取的MEAM势函数进行平衡驰豫，以拟合计算材料的主要晶胞平衡态晶格常数以及常温条件下材料模型的线膨胀系数，以验证本文所建立的类电池帆板材料模型与描述材料模型内原子间相互作用的MEAM势函数的合理性。

对材料模型的主要晶胞的平衡态晶格常数拟合计算以常温条件（300 K温度）为例，基于2.0Å～4.75Å的晶格常数构造包含500个原子的周期性边界类电池帆板材料模型，并都在300 K温度下以所选取的MEAM势函数做充分平衡驰豫，至2次时间步间材料模型的总势能变化小于设定阈值。随后计算材料模型的晶体结合能，并将模型的晶体结合能与对应的初始晶格常数进行拟合，找出对应最低晶体结合能的晶格常数值，此即为材料模型在300 K温度下的主要晶胞平衡态晶格常数。

图2为对300 K温度下类电池帆板材料模型的晶格常数与晶体结合能的拟合曲线，拟合结果显示此温度下，材料模型的主要晶胞平衡态晶格常数为a300K=2.8962Å，查阅手册［18］可得，与模拟的材料模型含碳量相近的20#钢在20℃（293.15 K）的温度条件下，主要晶胞平衡态晶格常数为2.8664Å，这与本文拟合计算结果吻合很好，相对偏差仅为1.04%。

图2 300 K下晶格常数-结合能曲线Fig.2 Curve of lattice constant and cohesive energy at 300 K

在400～1000 K的不同温度下，重复上述过程，分别拟合对应温度下的主要晶胞平衡态晶格常数，将之与温度进行线性拟合，并根据拟合结果与模拟得到的300 K温度下材料的主要晶胞平衡态晶格常数，按照式（1）对材料模型在300 K温度条件下的线膨胀系数α进行计算。

图3给出了对各个温度条件下拟合得到的类电池帆板材料模型的主要晶胞平衡态晶格常数与对应温度进行线性拟合的结果，其中拟合斜线的斜率为k=4.166 12×10-5Å/K，根据式（1）可得材料模型模拟所得的300 K温度条件下线膨胀系数为α300K=1.4385×10-5K-1。查阅手册［18］，20#钢的常温线膨胀系数为 α=1.42×10-5K-1，与模拟结果相对偏差为1.3%，较为接近；同时也与提供本文高超声速再入环境的计算条件来源文献［6］在计算钢制平板这一大型桁架航天器太阳电池帆板的简化再入模型时所采用的材料系数α=1.5×10-5K-1较为相近，两者相对偏差4.1%。

通过以上验证分析，证实本文针对类电池帆板分子动力学材料模型的构建方法与所选取的MEAM势函数能较为准确可靠描述材料的微观力学行为，可用于材料力学性能的模拟计算。

图3 300～1000 K温度-晶格常数图像Fig.3 Curve of tem perature and lattice constant from 300 K to 1000 K

3 分子动力学模拟方法与条件选取

3.1 仿真条件选取

为探究分子动力学在服役期满大型航天器再入大气层解体毁坏过程预报领域的应用前景，针对太阳电池帆板简化模型钢制平板的含碳钢材料（碳元素质量分数0.215%），使用分子动力学方法，研究材料的微观力学响应行为，分析材料力学性能与模型温度之间的关系，并在极端再入气动力热环境下模拟材料的力学性能极限与材料微观缺陷萌生演化至弹塑性失效过程。在模拟过程中，模型各轴向上均采用周期性边界条件，以此降低模型尺寸效应对模拟结果的影响，实现用微观层面模拟得到材料的宏观力学性能。

在对类电池帆板材料的微观力学行为与力学性能进行初步模拟时，构造尺寸为10a×10a×10a，包含2000原子的较小规模材料MD模型，在300 K、600 K、900 K、1500 K等不同温度条件下，分析材料的应力、应变，研究不同温度下材料模型应力随应变的变化规律，分析材料力学性能与温度的关系，为后续再入气动力热环境下材料的MD模拟奠定基础。

在对极端再入气动力热环境下材料的力学性能与力学行为进行模拟时，从处在Ma∞=8.37，Kn∞=0.01，γ=1.4的再入高超声速绕流环境中的服役期满航天器太阳电池帆板简化模型：尺寸为0.015 m×0.5 m的钢制平板变形升温至稳定的状态中选取MD模拟条件，其中高超声速再入平板近连续过渡流绕流流场的温度与压力分布通过求解Boltzmann模型方程的气体动理论统一算法（GKUA）［9-13，19］计算得出，而钢制平板模型在外流场气动力热耦合作用下的变形与平板内部温度增量分布则由基于热弹性动力学与热传导方程耦合求解材料动态热力响应的有限元算法（Finite Element Algorithm，FEA）［6，14-15，19］计算给出。

图4展示了GKUA计算得到的含碳钢平板在高超声速近连续过渡流绕流流场的温度分布情况［6］。分析流场分布可见，迎风面物面附近流场温度较高，气流经过拐角后迅速膨胀，进入背风区，流场温度较迎风区显著降低，并在后驻点物面达到最低。

图4 GKUA计算再入近连续过渡流区钢制平板绕流流场温度分布Fig.4 Temperature distribution of re-entry hypersonic flow field of vertical plate in near-continuum transition flow solved by GKUA

图5给出了使用FEA对处于上述气动力热环境中钢制平板模型进行计算模拟所得到的内部结构场温度分布，图中x、y轴的单位为m，模拟中时间步长为δt=0.05 s，结果的单位为℃。明显可见，模型内部温度增量较高的区域集中分布在迎风面附近，这与外流场温度分布规律一致。模型内部温度增量极大值出现在迎风面左上拐点处，此处边界曲率发生突变，结合图4结果可知，外流场热流也在此处达到最大，与计算结果相符。

对比FEA计算的时间步长δt=0.05 s与MD模拟的时间尺度（一般为ns量级），可认为在每次FEA计算的推进迭代中，MD模拟所关注的微观尺度材料的力学过程已经经历了足够充分的演化发展，因此可以使用具有周期边界的准静态MD模拟方法为FEA计算提供较为可靠的当地材料力学性能。从图4与图5中分析外流场中平板背风区温度与平板内部结构温度增量，可得到含碳钢平板内部的极限温度大致在1200～1300 K，由此，本文针对再入气动环境中类电池帆板材料的力学性能与微观力学行为的模拟选取在1300 K温度下，对具有周期性边界的材料模型施加载荷，并分析加载过程中材料模型中的粒子分布、应力-应变响应等进行分析，以研究材料在这一极端环境条件下的力学性能与失效过程。

图5 FEA计算再入钢制平板内部温度增量分布Fig.5 Temperature increment distribution in the inner of the p late under hypersonic re-entry flow solved by the FEA

3.2 载荷控制方法

分析不同工况的复杂应力环境中材料的力学性能时，常依照形状改变比能密度理论（Von Mises第四强度理论），认为畸变能密度达到极限时材料发生屈服，在应力上表现为材料Von Mises应力达到材料的极限。Von Mises应力可以通过式（3）根据材料应力张量的各分量值计算得出。

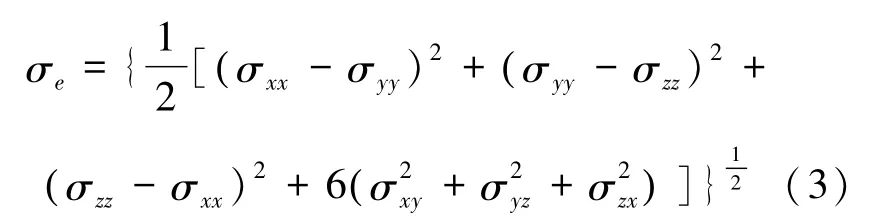
根据这一强度理论，本文选取恒定应变率载荷的单轴拉伸加载方式，来研究复杂受力条件下平板材料模型的Von Mises应力极限。具体加载方式为：将模型与x轴垂直的左端面固定，在右端面上施加大小为ε=2×1010s-1（0.02 ps-1）的恒定应变率的位移载荷，整个加载过程中设置恒温热浴控制模型的温度始终在所设定的模拟温度附近，并控制材料模型在未施加载荷的y、z方向上外压为零；加载过程每进行一段时间，就将模型在正则系综（NVT系综）下进行一次恒温弛豫，保持对材料模型的模拟始终处于准静态，并在每次弛豫后，对模拟体系的微观特性参数进行输出。

MD模拟的直接输出结果为系统内每个粒子在不同时刻的微观物理量，为此需要通过维里定理对粒子微观量进行系统平均，得到计算Von Mises应力所需的材料应力张量。维里定理如式（4）所示。

式中，Ω0为原子体积，Fij是第j个原子作用在第i个原子上的力，Mi、vi为第i个原子的质量和速度。

3.3 缺陷演化分析方法

研究材料在MD模拟中微观缺陷自萌生演化至材料屈服失效的过程时，主要分析材料内部粒子分布情况和材料Von Mises应力随应变的变化关系。而分析材料内部粒子分布时，除直接观察可视化处理后材料内部粒子排列，还常通过计算材料径向分布函数（RDF），进一步分析原子分布的无序化程度。在统计力学中，RDF g( r) 表示距参考粒子r处粒子的密度，若作归一化处理，则可得到gp( r) 为在r～r+d r范围内找到一个粒子的几率。若记p为系统的数密度，则RDF可由式（5）计算得到。

式中，R为原子的位置坐标，δ为Dirac符号，N为原子数。

4 类电池帆板材料的分子动力学模拟

4.1 初步模拟

对不同温度条件下规模较小（包含2000个原子）的类电池帆板材料模型在单轴拉伸载荷作用下的微观力学响应行为和力学性能进行模拟分析，并根据材料模拟结果计算分析材料的Von Mises应力与模型总应变的关系，研究并对比不同温度下材料的力学性能与力学极限，初步确认分子动力学模拟方法在服役期满航天器再入解体数值预报领域的应用前景与必要性。

图6绘出了不同温度条件下模型材料的Von Mises应力随应变的变化分布曲线，分析不同温度下材料模型的Von Mises应力随拉伸方向应变的变化规律，可以发现这些曲线具有相似的非线性变化分布特点。在拉伸过程中，不同温度条件下材料模型的Von Mises应力跟随拉伸方向应变的增加均会依次出现3个较为明显的峰值，并在第三峰值出现后断崖式下降至一个较小应力值，随后模型的Von Mises应力在一个较低的应力值附近随应变的继续增加而呈现出锯齿状波动的特点；在3个峰值中，前两峰的峰值应力相近，但相对于第三峰的峰值应力而言较小；第三峰为模型材料在模拟过程中材料模型Von Mises应力的最大值，而且在应力随应变增加达到此峰值之后所表现出的断崖式下跌与锯齿状波动特点与宏观材料拉伸试验中观测到的试样发生塑性屈服时展现出的应力-应变特性较为相近，由此可为此峰值应力材料模型在对应温度条件下的塑性屈服极限，在应力达到此峰值后，材料发生了塑性屈服失效。

图6 小规模含碳钢MD模型不同温度条件下Von M ises应力-应变曲线Fig.6 Von M ises stress-strain distribution at different tem peratures for small-scale carbon steel

进一步对比分析不同温度条件下模拟计算的结果，可以发现材料模型的Von Mises应力所对应的塑性屈服极限随着模型所处的温度提升而有所下降，在高温条件下下降尤为明显。在300 K的温度条件下，模拟所得的材料模型屈服极限为18.978 024 7×108Pa，所对应的拉伸方向上应变为0.586；温度升高至600 K和900 K时，材料模型的屈服极限分别下降至18.254 924 3×108Pa和15.643 999 4×108Pa，所对应的拉伸方向上应变分别问0.580和0.566；而当温度进一步升高至1500 K时，材料模型的屈服极限为6.353 825 4×108Pa，对应的拉伸方向上应变为0.544，此时的塑性屈服极限值刚刚达到常温条件下的33.5%。

根据3.1节中选取模拟条件时，对高超声速再入钢制平板在近连续过渡流绕流环境中内部温度的分析，钢制平板模型已经处在1300 K左右的高温条件中，而对于实际再入大气层的服役期满大型航天器来说，其板仓桁架结构在再入强气动力热环境作用下变形软化失效解体的过程中，所面临的温度条件将会与之相当甚至更加严酷，这意味着分析含碳钢板乃至服役期满航天器再入大气层所遇强气动力热环境结构的变形软化失效解体过程时，极其有必要引入MD方法，模拟分析再入气动环境计算得到的对应温度条件下的结构材料力学性能，使用MD实时模拟得到材料内部微观力学响应行为，为后续有限元算法计算材料结构的温度梯度与位移变形奠定实时动态气-固热力响应耦合模拟基础。

同时，由于模拟所用的MD模型规模较小，仅包含2000原子，在高温条件下，由于系统内粒子的能量较高，其相对于平衡位置运动的速度与范围也比低温条件有所提升，这使得低温条件没有显现的尺寸效应在高温状态有所显现，第三应力峰出现前原本较为平滑的分布轮廓线段处出现了较多震荡。因此，要在高温条件下较为精确模拟材料的微观响应、力学性能，需要构建较大规模的MD模型，通过统计平均抹平高温条件下微观系统的尺寸效应对材料性能模拟带来的影响。

4.2 再入气动环境下的分子动力学模拟分析

根据3.1节中选定的再入高超声速绕流环境类电池帆板材料的MD模拟条件，构建尺寸为80a×30a×30a、原子规模为144 000的MD模拟体系，并在1300 K温度下施加单轴拉伸载荷，逐步加载至拉伸方向上系统总应变至4.0，分析模拟过程中材料模型的内部粒子分布情况和材料的应力-应变关系，以研究材料在再入高超声速绕流环境下微观缺陷萌生演化至塑性屈服失效的过程。

图7（a）、（b）分别给出了模型经充分驰豫后，加载刚刚开始，系统总应变较小时（加载运行至6250时间步）与材料模型加载至32 500时间步时，材料模型在xy方向截面上的微观粒子分布情况，图片使用OVITO（Open Visualization Tool）软件对模拟结果进行可视化得到，图中红色符号代表Fe原子，蓝色符号代表C原子，白色空白代表晶状固溶体结构中的粒子间隙。图7（a）中，当模型应变较小时，体系内各粒子仍以较为均匀的晶体结构排布，晶格较大；图7（b）中，体系内粒子的排布较之应变较小时变得相对稠密，晶格变小，模型的粒子排布出现可以观察到的微观缺陷，图中白色符号集聚的区域显示了微观层面Fe、C原子在缺陷处变得稀疏，材料模型中微观缺陷萌生，这些微观缺陷的延伸拓展导致材料的弹塑性失效以致断裂毁坏。

图7 初始运行至32 500时间步时类电池帆板材料模型体系结构中出现较明显微观缺陷Fig.7 M icro-defects arisen in themodel system from initial run to Timesteps=32 500

图8绘出了材料应变逐渐增加过程中，材料模型的径向分布函数RDF的分布曲线。可以看出，随着拉伸过程的进行，材料模型RDF中峰的数量逐渐减少；同时峰的宽度逐渐增加，峰的高度不断降低。这说明随着材料应变的增加，内部原子分布的有序性逐渐降低，原本完美的空间晶格结构逐渐萌生缺陷。至观察到明显微观缺陷的32 500时间步时，材料模型的RDF曲线中清晰的4个主要峰已经模糊融合成2个，说明此时材料内部原子分布的无序性已经很严重，材料内微观裂隙缺陷已然萌生，随着这些缺陷进一步的演化延拓，维持材料空间晶格结构的原子键团簇破坏，材料逐步开始其弹塑性失效过程，直至软化熔融彻底毁坏。

随后对高超声速再入环境下类电池帆板材料的力学性能极限进行分析，计算材料拉伸过程中的Von Mises应力，并绘制Von Mises应力随拉伸方向上系统总应变的变化曲线，如图9所示。可以看出，此条件下对原子数量较大的材料模型进行模拟得到的应力应变关系，与初步模拟时所展现出的应力-应变分布的共性有相似之处，材料的Von Mises应力均跟随应变增加出现3个峰值后进入锯齿状波动增加的塑性屈服阶段，且材料对应的塑性屈服极限，亦即模拟过程中得到的Von Mises应力的最大值均出现在第3个应力峰值处，本文模拟所得结果为6.072×108Pa，对应的拉伸方向系统总应变为0.526；但图9的结果中，与初步模拟得到峰值相近的前两峰不同，第2个应力峰的峰值明显低于第一峰，而且在将模拟体系所包含的原子数目极大提升后，高温条件下由于尺寸效应带来的震荡不再明显，应变在达到第三峰对应的应变之前，图线的光滑度较之初步模拟有了明显的提升。

图8 1300 K温度条件下模拟得到的类电池帆板材料模型径向分布函数随位置距离r变化轮廓线Fig.8 RDF profiles along w ith r of battery-like sailboard material at 1300 K simulated by the present MD model

图9 再入环境类电池帆板材料Von M ises应力-应变曲线Fig.9 Von M ises stress-strain distribution of batterylike sailboard material in the X-direction at 1300 K under reentry environm ent

图10绘出了由基于准静态模型建立的经典材料强度理论分析方法的结构动态热力响应变形行为有限元算法，计算出的钢制平板模型升温变形至稳定阶段时，平板底部的Von Mises应力分布情况。根据图示结果，模型内部Von Mises应力在平板底部右下拐点的应力集中处达到极值，此处对应的Von Mises应力已超过9×108Pa，这远远超出了本文在对应条件下通过MD模拟得到的材料Von Mises应力强度极限6.072×108Pa。这说明，钢制平板在高超声速再入绕流气动力热环境中，达到FEA计算结果收敛的稳定状态前，模型内就已经发生了塑性变形，材料的力学性能发生了不可逆变化；同时说明了服役期满航天器在其再入过程中，发生首次解体时，航天器太阳电池帆板在高超声速气动力热环境作用下所受应力、温度还未达到弹塑性失效屈服应力极限与软化温度［6，15，19-21］，其原因极可能是其结构材料内部微观裂隙缺陷萌生演化直至断裂毁坏，本文尝试搭建起来的MD模拟平台初步揭示了这一变化过程，进一步细致研究有待后续深化。为更为细致模拟该平板再入过程的升温、变形至毁坏的过程，应在模型内Von Mises应力分布极值达到MD计算得到的Von Mises应力强度前，通过FEA计算其结构内部温度、应力分布，再通过MD方法分析确定对应状态下的弹塑性模量、线膨胀系数、热导率等物性参数，作为输入反馈回FEA计算，将结构材料在再入气动环境作用下力学性能变化纳入结构变形失效分析的过程中，这也为本文所做工作的未来发展指明了方向。

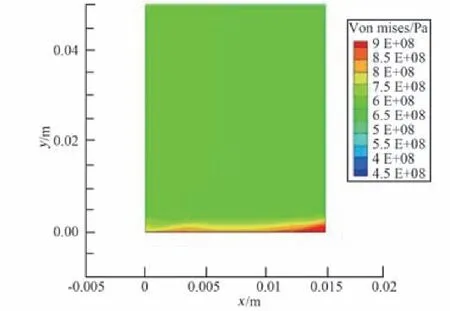
图10 再入高超声速环境中稳态时平板底部Von M ises应力分布Fig.10 Von M ises stress distribution of p late at bottom in reentry steady state

5 结论

1）在拉伸载荷作用下，碳元素质量分数为0.215%的二元组分含碳钢材料模型的Von Mises应力-应变分布具有相似的变化规律，随着应变载荷的提升，应力依次出现3个峰值，材料在应力达到第三峰值所对应的Von Mises应力强度极限后，进入塑性屈服阶段。

2）随着模型模拟温度的提升，含碳钢材料模型模拟得到的Von Mises应力强度极限会降低；在高超声速绕流环境的条件下，材料模型Von Mises应力的力学性能极限为6.072×108Pa，在应变0.526时达到，这一力学性能极限远低于通过FEA方法计算出的材料内部应力最大值，说明钢制平板在达到有限元计算的稳态前，其内部材料就已经发生了塑形屈服失效，力学性能已经发生了不可逆的变化。

3）本文同时通过分析材料模型在加载过程中内部微观粒子的排列分布变化规律，对材料模型内部微观缺陷萌生演化发展过程进行了模拟，在具有晶体结构的含碳钢合金中，随着载荷的加载，材料内部粒子排布的无序性会增加，局部粒子排布出现空隙，并在此基础上演化发展为微观缺陷，直至材料发生塑性屈服失效等宏观毁坏。

本文所采用的计算模型是较为简单的二元合金晶体结构，仅包含Fe、C 2种元素组分，在实际的航天应用中，所使用的材料多为组分复杂、工艺特殊材料，作为初步阶段性工作，尚难以直接模拟这些复杂金属（合金）材料微观力学行为；模拟过程中的加载方式是根据形状改变比能密度理论以单轴拉伸替代实际工程中的复杂应力条件，这在微观层面是否完全准确可靠也需要未来进一步验证确认；同时本文将分子动力学方法引入到金属桁架结构服役期满航天器陨落再入过程仿真分析的初步探究，计算规模较小，尚未达到可以实际应用的程度；而如何实现将MD方法与FEA方法进行有机耦合，实现二者计算结果互为输入，彼此修正，形成闭环，这些是后续深化与发展方向，有待进一步探索研究。