类天宫飞行器轨道衰降过程空气动力特性一体化建模并行优化设计
2020-09-02张子彬李志辉白智勇彭傲平
张子彬,李志辉*,白智勇,彭傲平
(1.中国空气动力研究与发展中心超高速空气动力研究所,绵阳621000;2.北京航空航天大学北京前沿创新中心国家计算流力学实验室,北京100191)
1 引言
航天器轨道计算与飞行航迹数值预报的准确可靠直接依赖于轨道动力学方程空气动力项求解的快速高效[1],研究建立适于大型航天器在轨与服役期满轨道衰降过程全飞行流域高超声速空气动力特性一体化模拟平台[2]与融合修正沿轨道空气动力一体化快速计算方法是关键基础[3]。当航天器运动在200 km以上时,飞行绕流已属于高稀薄自由分子流,此时气体分子平均自由程将超过200 m,Knudsen数将大于10。对于这种情况,传统观点认为航天器飞行阻力、升力等空气动力将不再随飞行高度发生变化,因此应该采用固定的气动力系数参与飞行动力学轨道控制的[3]。但是,中国天宫飞行器在采用固定阻力系数2.2开展低轨道飞行试验时,发现有时飞行偏差越来越大,须使用RCS姿控系统强制控回原标称轨道,造成燃料消耗,甚至难以准确有效控制[4]。因此,提出这样的问题:天宫飞行器低轨道飞行所受大气阻尼系数是否会变化?为了解决这一问题,李志辉等[4]使用修正Boettcher/Legge非对称桥函数,发展了适于高超声速稀薄过渡流区气动力计算的当地化桥公式法,建立了专门针对复杂巨大的天宫飞行器跨越大气层不同高度、不同马赫数、不同迎角与侧滑角空气动力特性快速计算方法与程序软件,以减小数值计算工作量,并融合弹(轨)道飞行动力学计算推进,得到了具有实用价值的结果。实际应用发现,在空气动力融合轨道飞行航迹数值预报过程中,该类算法程序的运算速度与能力效率仍有待进一步提升[3]。为此,本文研究基于CUDA架构的GPU异构高性能并行计算技术,开展大型航天器轨道衰降过程空气动力特性一体化建模并行优化设计与应用尝试。
随着科学技术的迅猛发展,高性能计算已成为科学技术发展和重大工程设计中具有战略意义的研究手段[5]。早期计算机性能的提升主要依赖CPU(中央处理器)主频的提升,但由于CPU的功耗与频率的三次方近似成正比,无限制地提升频率已不可能。到2003年,CPU频率的提升接近停止[6]。为了应对这一情况,人们往往采用基于CPU的并行计算方法来解决这一问题(例如消息传递接口,简称MPI),但由于单个的CPU最多只能集成十几、几十核,导致基于CPU的并行计算能力受到很大限制。
2007 年,随着基于英伟达CUDA架构图形处理单元(GPU)硬件的出现,集成核心的能力比CPU要强大得多(例如,英伟达Tesla架构的K20X芯片包含2688个核心),这使得GPU的运算能力比CPU更胜一筹[7]。除此之外,CUDA架构不但包含英伟达GPU硬件,而且包含一个软件编程环境,在这样的编程模型下,CPU负责整个任务的流程控制和任务的串行计算,而GPU采用并行算法完成任务中计算密集部分的计算,人性化的编程环境有力助推了GPU的广泛应用。
时至今日,GPU和并行技术的使用已成为当今数值计算的潮流和趋势,并被广泛应用于包括计算流体力学在内的许多领域。同样地,它们也为求解稀薄气体流动问题提供了一条行之有效的途径。特别是使用NVIDIA的Tesla GPU在计算流体动力学中的应用加速明显,针对不可压缩的纳维—斯托克斯(Navier-Stokes)方程数值求解模型的并行实现,在1024×32×1024的规模下使用4个Tesla C870 s与使用AMD Opteron 2.4 GHz的性能相比约提高100倍;针对格子Boltzmann方法在格子大小128×128规模下,使用Tesla 8-series GPU相比于使用Intel Xeon的性能约提高了130倍[8]。可见,GPU和CPU融合的并行架构是未来加速通用计算必然趋势。
本文基于英伟达CUDA架构的GPU,以微型计算机为平台,根据近地轨道类天宫飞行器空气动力特性当地化桥函数关联快速算法的运算流程及对应程序软件的编写特点,提出相应并行优化方案,并付诸实施,以提升程序计算效率,减少程序运行时间。并以类天宫一号目标飞行器无控飞行轨道衰降过程空气动力特性一体化建模作为算例,给出其在低轨道飞行过程相应高度飞行绕流状态的气动特性,检验检测本文并行计算模型方案的并行加速有效性与高效率,以此为基础,逐步开拓GPU并行计算在融合弹(轨)道数值预报关于空气动力计算的快速高效与准确性。
2 空气动力特性当地化计算方法
融合航天器在轨飞行与离轨再入飞行航迹弹(轨)道数值预报的跨流域高超声速空气动力计算所用的当地化计算方法,是基于自由分子流与连续流当地桥函数理论关联的桥公式法[9-10]。自由分子流和牛顿连续流作为航天器再入飞行过程2个对应极限流态,其中稀薄过渡流区域的气动力系数可以用当地气动力的解析来表述,当地面元气动力系数采用基于自由分子流与连续流的当地化桥函数光滑搭接[11]。这是一种加权函数,依赖于独立的关联或相似参数(如克努森数Kn),通常由实验结果与数值计算分析确定。桥公式法根据自由分子流和牛顿连续流不同的物理定律,采用两个不同的数学函数FCont和FFM来描述,而在中间区域给出一个新的函数Fb,即桥函数。由此,对于给定的入射角θ,当地面元上经归一化压力和摩擦力系数表达为式(1)[1]:

式中,Fb,p和Fb,τ分别是压力和摩擦力桥函数,依赖于独立参数Kn、TW/T0和θ。
对过渡流区域,当地桥公式[12]可以提供依赖于独立参数的归一化压力系数和摩擦力系数。当地桥函数的表达式有许多种,本文研究发展修正的Boettcher/Legge非对称桥函数表达式,其中,非对称的压力桥函数可表示为式(2):

式中,Knn,p、ΔKnp1、ΔKnp2根据飞行器外形及绕流特点为可调关联参数。
非对称摩擦力桥函数可表示为式(3):

发展可分段描述的非对称压力与摩擦力系数关联桥函数快速计算模型,需要根据飞行器外形及绕流特点调试确定Knn,p、ΔKnp1、ΔKnp2及Knn,τ、ΔKnτ1、ΔKnτ26个关联参数,由于天宫飞行器的大尺度复杂结构与在轨飞行跨流域多尺度非平衡绕流特点,需要依靠高性能大规模并行计算机开展求解Boltzmann模型方程气体动理论统一算法等跨流域空气动力学数值计算典型飞行状态模拟结果[2],最优拟合计算修正确定,使当地化工程计算结果最大程度地满足实际计算精度[9]。
关于飞行器物形处理,选取一种较为通用和近似的面元非结构网格物形表征处理方法[4],将飞行器物面划分为若干个面元,利用四边形或三角形来逼近复杂外形,图1绘出类似表征天宫飞行器两舱体的大尺度圆柱体计算模型表面三角非结构网格布局,可计算出每个面元的中心点坐标、中心点处的法向及面元面积[13]。由于类天宫飞行器属于复杂非规则巨大板舱组合体,为了解决类天宫飞行器及附件复杂物形表征的困难,引入分区网格与非结构网格生成技术,进行复杂物形表征处理,以便计算面元所受气动力,将所有面元上的气动力加起来就可以得到整个飞行器的气动力。
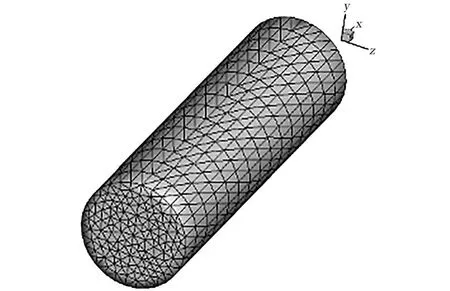
图1 类天宫飞行器两舱体圆柱体外形表面非结构三角形面元网格Fig.1 Unstructured triangular surface elementmesh on cylinder surface for two-capsule body of Tiangong type spacecraft
3 并行优化方法
传统的空气动力特性当地化计算程序没有采用并行方案,因此只能使用其中1个核心和1个线程,且每次只能执行1次循环,造成了计算资源的闲置与浪费。为了满足气动融合轨道飞行航迹数值预报对空气动力特性实时计算快速高效要求,需要发展多核处理单元的并行优化方法[14]。
为此,对类天宫飞行器空气动力特性当地化算法的运算流程及对应程序代码进行整体分析发现:
1)程序热点代码较为集中。原有程序主要执行的代码集中在算法的求解部分,具体表现为多个连续的3层嵌套循环。其中最内层的循环次数最多,达到十万级别,适合数百个以上核心同时计算,有利于发挥GPU设备的性能优势。
2)数据依赖性较弱。数据依赖是指下一条对数据操作的指令必须等待上一条操作该数据的指令完成。原程序各个循环间保持相互独立,不存在数据依赖关系,有利于发挥GPU设备的性能优势。
3)循环内外数据传输需求较少。长期以来,GPU与CPU之间数据传输较慢,一直是GPU在应用过程中的诟病。具体来说,由于GPU与CPU之间的数据传输速度远低于GPU、CPU芯片与各自寄存器的传输速度,甚至不及CPU与内存、GPU与显存之间的传输速度,因此造成引入GPU设备被迫增加的数据传输时间,会小于引入GPU设备所节省时间的情况,即损耗大于收益。而本文所涉及的程序由于循环内外数据传输需求较少,可以避免这一情况,因此有利于发挥GPU设备的性能优势。
由上述特点可见,原有程序拥有改写为并行程序的潜力,并可以较好地发挥GPU设备的性能优势。因此,针对原有程序的编写特点,我们引入CUDA架构的GPU设备,根据调试过程中出现的问题,分别采用系统级别、算法级别以及语句级别3个层次的优化手段对其进行优化。
3.1 系统级别优化
系统级别手段优化主要考虑程序性能的控制因素。对本文要解决的问题,首先分析原程序是否存在以下3个限制因素:①处理器利用率过高还是过低;②存储器带宽利用是否不足;③阻塞处理器运算的其他因素。
CPU、GPU及存储器连接关系如图2所示,测试发现,GPU与CPU以及GPU与显存的数据传输速度比较缓慢,因此对这两部分着重进行了优化设计如下:
1)对齐访问。由于在GPU显存数据传输时,可以通过32、64或128 Byte的作业来访问,这些作业都对齐到它们的尺寸。因此未对齐的访问会增加访问次数,浪费传输资源。就本程序而言,由于算法使用GPU运算时有很多零散的参数需要传入,因此将其整合为一个数组,进行一次性传输,方便访问数据的对齐。图3为本文设计使用的GPU内存对齐访问格式。

图2 CPU、GPU及存储器连接关系示意图Fig.2 Connection diagram of CPU,GPU and correspondingmemory
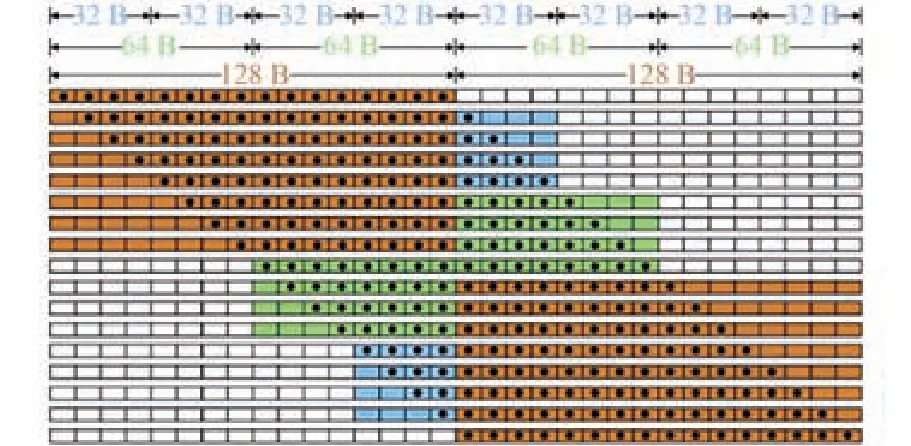
图3 基于CUDA架构的GPU内存对齐访问Fig.3 Aligned access of GPU memory based on CUDA
2)使用数据传输函数。由于GPU设备传统的数据传输方式效率较低,因此高版本CUDA架构的GPU设备提供了丰富的数据传输函数,可以完成CPU到GPU或者GPU到另一台GPU设备的数据传输,通过测试,可选用cudaMemcpy函数作为传输接口,具体格式为:cudaMemcpy(dst,src,count,kdir)。其中,dst、src分别为目标变量和源变量,count为拷贝的数据长度,kdir为可省略参数。
3.2 算法级别优化
算法级别的优化通常涉及程序部分,而这部分包含一个或多个函数,甚至只有一段语句。算法级别优化主要涉及算法实现时要考虑的问题,通常算法要考虑数据的组织、算法实现的策略。
一般串行算法求解的程序部分表现为多个连续的三层嵌套循环,且循环主要集中在最内层,达到十万级别。以NVIDIA公司的GTX750Ti图形处理单元为例,它拥有640个计算核心,理论上可支持131 072个线程同时计算[14]。从线程数来说,每个循环都可以交给一个指定的线程进行计算,具有较好的并行性;从核心数来讲,十万余个循环可以拆分给多个GPU芯片共同完成,具有较好的可扩展性。
因此,本文将算法求解部分的最内层循环经过展开与合并处理后,整理为一个循环,再整体移植入核函数,从而利用GPU强大的并行计算能力提升运算效率。具体代码如下所述。
原有串行程序代码为:
do i=1,ntr!ntr=121822
……!数组的循环运算A
end do
……!数组的共同运算B
do i=1,ntr!
……!数组的循环运算C
end do
……!数组的共同运算D
经过优化的程序代码为:
attributes subroutine CUDA(input,output)
!GPU设备核函数开头
do i=1,ntr!ntr=121822
……!运算A+B+C+D
end do
end subroutine
3.3 语句级别优化
语句级别的优化包括对函数、循环、指令等语句细节的优化。
CUDA架构的GPU设备显式地将存储器分成4种不同的类型:全局存储器(globalmemory)、常量存储器(constantmemory)、共享存储器(share memory)或称局部存储器(localmemory)、私有存储器(private memory)。虽然其中除全局存储器有较大容量之外(如tesla K20全局内存为5 GB),其余3种存储器的存储容量只有64KB左右[14],但是这4种存储器的读取速度却有很大差异:全局存储器是最慢的,其延迟为几百个时钟;常量存储器次之,延迟为几十个周期;共享存储器的延迟在几个至几十个时钟周期之内;而私有存储器通常就是硬件的寄存器,它是GPU的存储器中读取最快的,几乎不用耗费时间[14]。而相比较全局变量耗费的几百个周期,1个时钟周期可以做4次整形加法、2次浮点乘加,3个周期可以做一次乘法,十几个周期可以做一次乘法[15]。因此如果能够合理利用常量存储器、共享存储器和私有存储器,尽量减少读取全局存储器所产生的时间耗费,那么所产生的收益将是相当可观的。
以下列出了私有存储器、共享存储器和常量存储器的声明使用方式:
integer::t,tr! 使用私有存储器
real,shared::s(64) ! 使用共享存储器
real,parameter::PI=3.14159! 使用常量存储器
4 算法验证与结果分析
将所建立类天宫飞行器空气动力特性当地化串行算法及对应程序按提出的并行计算方案进行CPU+GPU移植优化后,对类天宫一号目标飞行器外形进行运算,分析优化前后程序运行性能。
4.1 计算模型与条件
实施对于天宫一号目标飞行器低地球轨道飞行过程气动力系数一体化计算,采用基于三角非结构网格表征物面,绘出计算模型表面三角非结构网格布局如图4所示。
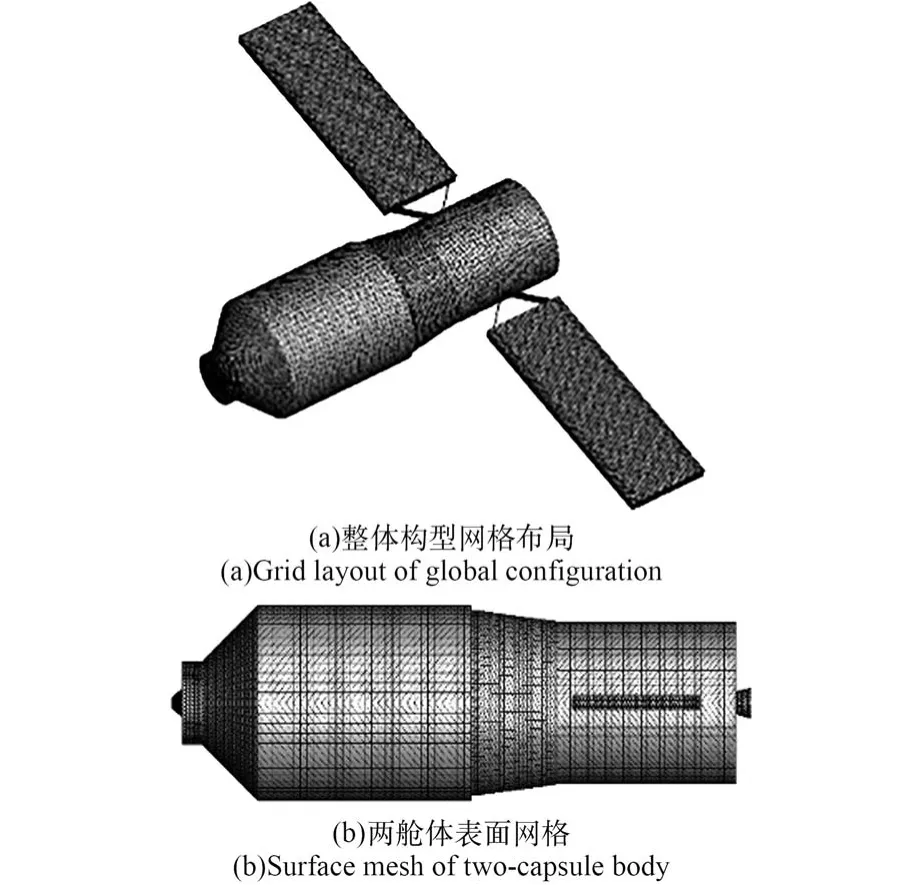
图4 天宫飞行器计算模型表面非结构网格布局Fig.4 Unstructured triangular surface elementmesh on the com puting model of Tiangong spacecraft
关于极不规则大型复杂结构航天器气动特性计算,参考面积选取可分为2部分考虑:第一部分是本体迎风面积,即飞行器本体的底面积;第二部分是帆板的迎风面积,由于太阳电池帆板需要围绕中心轴转动,于是帆板迎风面积采用等效面积计算;总的参考面积为上述两部分面积之和[4]。
本算例采用多核CPU+GPU架构计算机进行运算,CPU及GPU性能参数见表1所列。对比试验中,串行程序仅由CPU独立完成,共调用1个核心和一个线程。并行程序的算法求解运算由GPU完成,调用640个核心和131 072个线程,其余步骤如数据载入、结果收集及试验监测等过程仍由CPU完成。

表1 试验设备性能列表Table 1 Performance list of test equipments
4.2 GPU并行算法与CPU串行计算结果验证
图5与图6分别绘出天宫飞行器角α为22°,阻力系数与升力系数随侧滑角β变化趋势其中蓝色曲线表示CPU串行程序计算结果,而红色方格代表并行程序计算结果。由图看出,两者完全吻合,本文经过对156次计算结果进行统计,除部分个别数值末位略有不同且结果仅差0.000 01,误差缘由可能是CPU和GPU芯片取舍原则不同所致,其余数据完全一致,这种GPU与CPU计算的高精度一致性,进一步证实本文GPU并行算法实现的正确性与高效率。
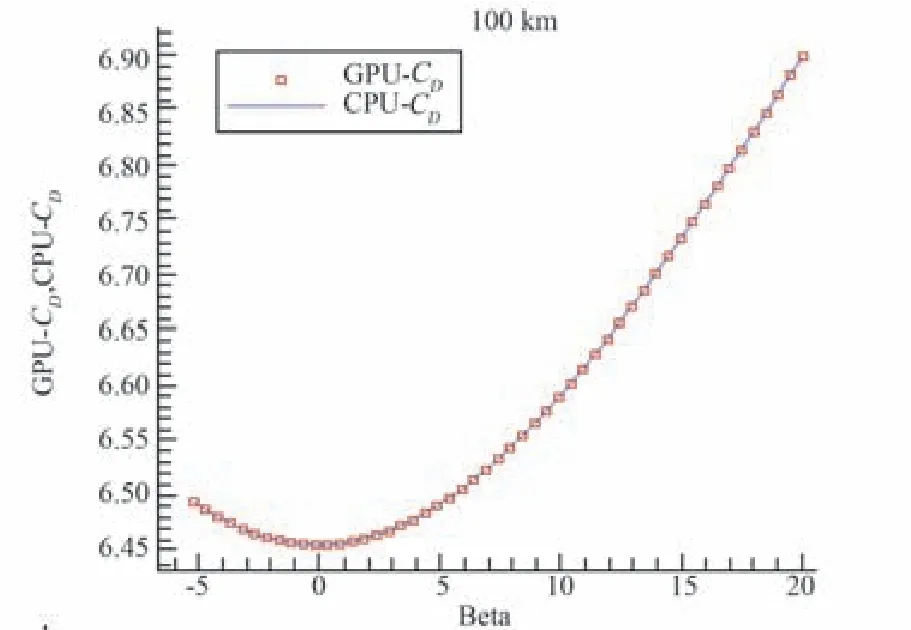
图5 GPU加速前后阻力系数随侧滑角变化计算验证Fig.5 Computing verification of drag variation w ith sideslip angle before and after GPU acceleration

图6 GPU加速前后升力系数随侧滑角变化计算验证Fig.6 Com puting verification of lift variation w ith sideslip angle before and after GPU acceleration
表2列出原串行程序CPU计算与本文GPU并行算法程序及优化后的GPU并行程序在求解过程中,单步求解各模块程序段的平均消耗时间,其中GPU运算是在GPU中发生的过程,数据归约是在CPU中各节点进行。由表2看出:①GPU并行程序虽然增加了数据输入、输出的过程,但总的运行时间仍比CPU串行程序计算时间有了明显减小;②经过并行优化后,数据在CPU与GPU之间传输的时间也有了明显减少。
表3给出了CPU串行、并行及引入GPU设备并优化后的程序平均消耗时间,从表中可以看出,受制于CPU线程与计算核心数影响(CPU i7-4770 K只能使用8个线程与4个处理单元),CPU并行程序在单步求解时间方面的加速比只能达到7.0左右,而无法超过8,而GPU设备的相应加速比可以达到13.0,受此影响,CPU并行程序与优化后的GPU并行程序的整体加速比仍有一定差距,虽然近年来CPU的最大线程数和性能有所提升,但GPU设备的并行能力也在大幅度增长,因此仍然没有实质性的区别,这样的案例进一步说明了采用GPU并行的重要性和研究价值。

表2 算法单步求解各阶段平均消耗时间Table 2 Average runtime per step in solving process/ms

表3 CPU串行、并行及GPU优化后程序平均消耗时间Table 3 The average runtime time of CPU serial program,parallel program and GPU optim ized program
4.3 性能分析
根据常用并行算法性能衡量手段,采用加速比对计算试验进行分析。加速比的定义为顺序执行时间与并行执行时间比值。由表3可知,CPU串行程序消耗时间0.747 h,GPU并行程序消耗时间0.140 h,因此加速比为5.3,这说明,将GPU并行加速引入类天宫飞行器无控飞行轨降再入解体过程气动力系数一体化计算相当快速高效。
比较分析还可看出:
1)在单次求解过程中,CPU循环运算平均消耗75.5 ms,而优化后的GPU运算平均消耗5.8 ms,GPU并行计算加速比约为13。可见,第3章引入GPU设备、发展的GPU并行优化策略是行之有效加速手段;
2)通过优化,单次求解过程中的数据传输耗时由原来的9.2 ms降为2.1 ms,减少了77%;数据归约耗时由原来的2.0ms降为0.7 ms,减少了65%;GPU运算过程也由原来的4 ms降为3 ms;合计时间由优化前的GPU运行时间15.2 ms降为5.8 ms,减少了61%。可见,本文介绍的GPU优化手段成效显著;
3)在试验中共使用线程512×256=131 072个,而GPU计算核心仅调用640个,这是因为每个核心上被分配了多个线程,这增加了线程等待时间,因此,当调用核心数增加时,程序仍有进一步扩展的空间;
4)在单次求解过程中,GPU并行程序数据输入输出的平均耗时为2.6+6.6=9.2 ms,是单次求解过程平均耗时(15.2 ms)的近60%,即使在GPU并行优化后,输入输出的平均耗时为0.9+1.2=2.1ms,是单次串行求解过程平均耗时(5.8 ms)的近36.2%。可见,由于GPU与CPU之间的传输速度过慢,输入输出占用了GPU调用的相当多时间,因此,如何发展高效快速的输入输出仍是限制GPU推广应用需要进一步研究解决的瓶颈之一。
4.4 类天宫飞行器轨道衰降过程空气动力特性计算分析
使用类天宫飞行器轨道衰降过程空气动力特性一体化建模GPU并行算法程序,对天宫飞行器无控飞行轨道衰降过程340~120 km气动特性详细计算,图7与图8分别绘出太阳电池帆板面与天宫飞行器本体主轴夹角10°、迎角α=10°进行340~120 km不同高度340 km、260 km、180 km、140 km、120 km的气动阻力、升力随不同侧滑角变化轮廓。可看出对于所计算的不同飞行绕流状态,均在侧滑角β=0°阻力系数最小、升力系数最大,说明天宫飞行器存在严重的板舱非规则构型,一旦无控飞行姿态出现侧滑角飞行绕流现象,迎风面积、阻力系数都会迅速增大,升力系数快速减小,致失稳加速飞行绕流状态,印证了天宫一号目标飞行器无控飞行轨降过程数值预报发现的,其自2017年9月初出现失稳后三轴旋转加速直至最终再入大气层解体的无控飞行绕流现象。

图7 天宫飞行器轨道衰降过程气动阻力系数GPU优化并行计算结果与CPU串行计算验证Fig.7 Verification of GPU parallel program and CPU serial computation for aerodynam ic drag variation of Tiangong spacecraft during orbital declining at 340~120 km
图9(a)、(b)分别绘出太阳电池帆板面与天宫飞行器本体主轴夹角10°、α=22°、β=0°时天宫一号目标飞行器轨降进入临近再入段240~120 km不同高度240 km、220 km、200 km、180 km、160 km、140 km、120 km的气动阻力、升力系数随飞行高度变化趋势。可看出对于所计算的不同飞行绕流状态,随着高度降低,阻力系数、升力系数呈现快速非线性下降趋势,印证了天宫一号飞行航迹在此高度轨降过程中,将于20 d内到达120 km再入大气层解体坠毁的无控飞行变化现象。
5 结论
1)通过分析近地轨道类天宫飞行器空气动力特性当地化桥函数关联算法及其对应程序具有多连续三层嵌套循环热点代码集中、循环间彼此独立不存在数据依赖关系及循环内外数据传输需求少等特点,引入了CUDA架构的GPU并行加速设备,提出了基于多核处理单元的并行优化设计方案。

图8 天宫飞行器轨道衰降过程气动升力系数GPU优化并行计算结果与CPU串行计算验证Fig.8 Verification of GPU parallel program and CPU serial computation for aerodynam ic lift variation of Tiangong spacecraft during orbital declining at 340~120 km

图9 天宫飞行器轨道衰降过程气动系数随飞行高度GPU并行优化计算与CPU串行计算验证Fig.9 Verification of GPU parallel program and CPU serial com putation for aerodynam ic drag and lift variation of Tiangong spacecraft during orbital declining at 340~120 km.
2)针对气动融合轨道数值预报快速高效特点,发展了系统、算法、语句级别的3个层次并行优化方法。建立了基于GPU内存对齐访问格式与数据传输函数方案、循环展开与合并、优化存储器使用等CPU+GPU并行移植优化技术,快速提升了GPU数据传输速度和运算效率。
3)经本文GPU并行算法与CPU串行计算试验验证表明,类天宫飞行器空气动力特性当地化工程算法程序经GPU并行移植优化后,运行程序消耗时间由CPU串行计算0.747 h,减小至GPU并行计算0.140 h,并行加速比为5.3,证实首次将GPU并行加速引入类天宫飞行器无控飞行轨降再入解体过程气动力系数一体化计算相当快速高效。
4)GPU作为图形处理工具,在架构上为了集成更多的计算核心而牺牲了存储性能和单核计算能力,GPU虽然在并行加速能力上远胜于CPU,但是在数据传输及单核处理能力方面较弱。计算程序只有在被改写成数据依赖性好,传输需求少、计算量大的运算模式,才能发挥GPU设备优势。本文提出的并行优化设计方案,可以为其他算法程序在大规模并行计算实现方面提供经验和借鉴参考。
5)本文工作属初步阶段性,将GPU并行移植优化算法应用于其他跨流域空气动力学数值模拟方法,特别是GPU与CPU之间传输速度慢,输入输出占用GPU调用较多时间,如何发展高效快速的输入输出是限制GPU推广应用瓶颈,均有待进一步研究解决。
