有限体积格子Boltzmann方法用于近空间连续流区绕流模拟

皮兴才，李志辉*，彭傲平，张子彬

（1.中国空气动力研究与发展中心超高速空气动力研究所，绵阳621000；2.国家计算流体力学实验室，北京100191）

1 引言

服役期满的航天器将再入、解体并进入近空间飞行环境。由于稠密大气对解体物的气动力、热作用，大部解体物会在再入过程中熔融、烧蚀、蒸发消亡掉。但随着飞行高度、速度、能量不断降低，至少10%～40%质量的残骸碎片存留，形成板、方/圆柱、球形物等不同类型的残骸，陨落到地面，可能对人财物、生态系统安全造成威胁［1-2］。

格子Boltzmann方法（Lattice Boltzmannn Method，LBM）起源于格子气自动机方法，由Mc-Namara和Zanetti提出［3］，并由Higuera［4］将其应用到实际的流体力学数值计算中。目前已经成为一种新的计算流体力学及数值传热学分析方法，被广泛应用于多孔介质流动、多相流动、微流动等问题分析。

为了保证离散守恒性，标准LBM的平衡态分布函数由Boltzmann方程的经典解析解：Maxwell平衡态速度分布函数作小Ma数Taylor展开获得。这使得通过Chapman-Enskog展开标准LBM获得的宏观流动物理量方程是具有Ma2量级的附加项的不可压缩Navier-Stokes方程［5］。因此，标准LBM被视为求解不可压缩流动的压力修正方法［6］。为了使格子Boltzmann方法能分析可压缩流动，Shi等［7］提出的求解可压缩Euler方程的格子Boltzmann模型，Chen等［8］提出的求解可压缩Navier-Stokes方程的格子Boltzmann模型。但这些模型无法实现比热比γ的可调，且其还原的比热比不满足实际物理意义。Kataoka等［9］提出的多速度格子模型克服了上述问题，并被成功应用到Ma小于1的可压缩粘性流动模拟。

为了使LBM方法具备高马赫数可压缩流动的模拟能力，Qu等［10］提出用圆函数替代经典的Maxwell平衡态分布函数来构造格子Boltzmann离散速度模型，并确保圆函数满足恢复可压缩N-S方程所需要的矩关系，成功应用于可压缩流动模拟。这样的模型构造思路吸引了众多研究者：如Li等［11］将其与耦合双分布函数（Coupled Double Distribution Function，CDDF）Boltzmann模型方程结合，成功应用于Riemann问题、双马赫反射、Couette流等经典流动问题的模拟，并实现了普朗特数Pr、比热比γ任意可调；Qiu等［12］将该方法成功应用于可压缩边界层、激波边界层干扰等流动模拟；Gan等［13-14］采用高阶离散平衡态分布函数模型，构造了满足更复杂动理学矩关系的离散Boltzmann模型，成功将格子Boltzmann方法由可压缩连续介质流域模拟扩展到Burnett层面的可压缩近连续流模拟，并揭示了更具普适性本构关系，为高速可压缩流动中的热力学非平衡效应研究提供了新的建模思路。

综上可看出：LBM在求解可压缩流动方面，已从发展之初的格子气思想，逐渐过渡到利用Boltzmann介观思想构造求解流体物理问题的数学关系，并采用格子速度模型进行模型构建阶段。但这些可压缩格子模型在高马赫数流动中应用案例还鲜有体现。为将LBM推广应用于服役期满航天器再入解体残骸碎片的可压缩流动问题，本文将构造有限体积格子Boltzmann数值格式，求解耦合双分布函数模型方程以表征非平衡属性，并采用以圆函数为基础发展的D2Q13离散速度模型表征平衡态，由此建立适于近空间连续流区非规则残骸碎片绕流模拟的有限体积隐式格子Boltzmann方法，并在对Riemann问题、平板双马赫反射、RAE2822翼型跨声速绕流模拟验证基础上，开展近空间多次解体形成的残骸碎片简化方柱模型超声速绕流计算及其与N-S方程解算器结果对比检验，分析经改进的格子Boltzmann理论模型在模拟近空间连续流区残骸碎片绕流模拟潜力。

2 理论模型

因耦合双分布函数Boltzmann模型方程［11，15］的普朗特数Pr、比热比γ任意可调，且具有良好的数值稳定性，本文采用它作为控制方程。其密度及能量分布函数的演化方程如式（1）所示：

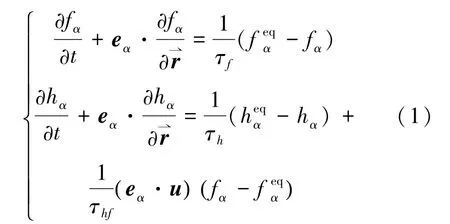
式中，下标α代表不同的离散速度编号，fα是密度分布函数，hα是能量分布函数。是平衡态密度分布函数，是平衡态能量分布函数。eα是离散速度矢量，u是宏观速度矢量，τf与τh分别是密度分布函数松弛时间及能量分布松弛时间，其满足关系式（2）：

普朗特数Pr与松弛时间的关系为式（2）：

为了使演化方程通过Chapman-Enskog多尺度展开后能够还原到可压缩N-S方程，平衡态密度分布函数及平衡态能量分布函数需要满足如式（4）所示关系式：

为了满足上述关系，本文采用基于Qu提出的圆函数重构平衡态分布函数的D2Q13离散速度模型［10-11］。D2Q13离散速度模型如式（5）所示：

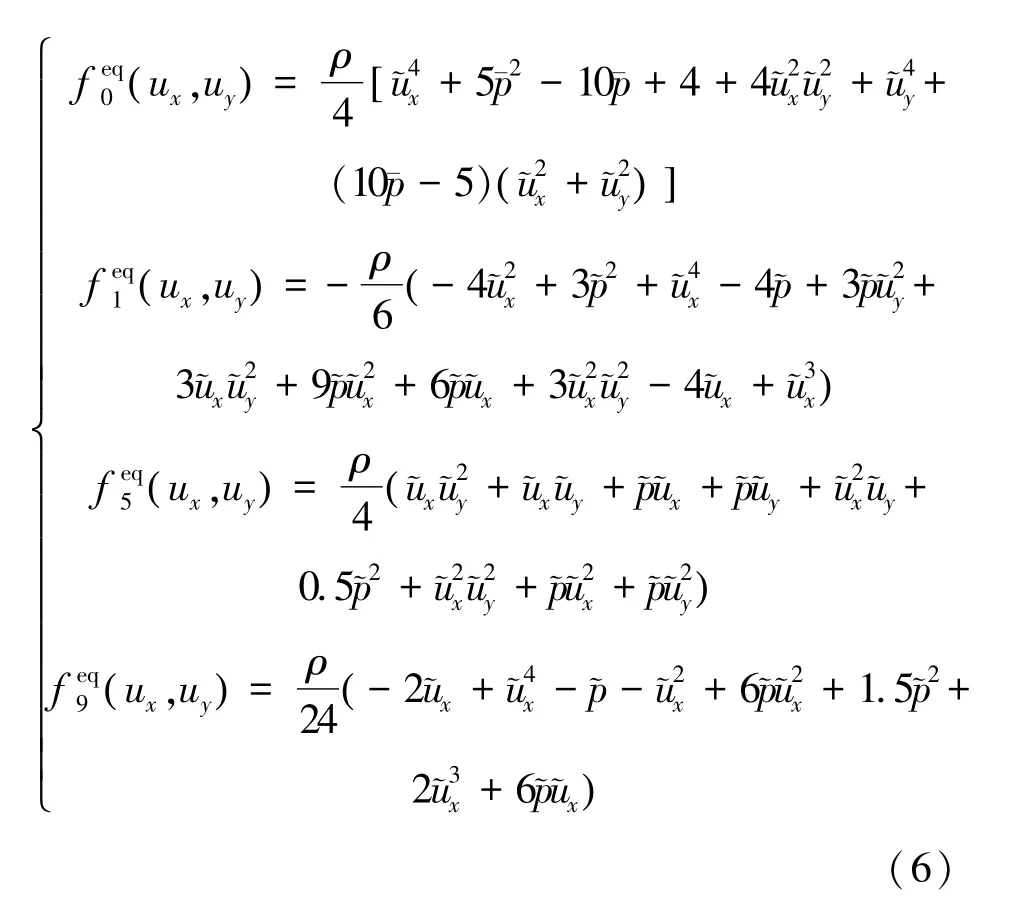
其他离散速度点的平衡态密度分布函数满足式（7）：

各离散速度点的平衡态能量分布函数见式（8）：

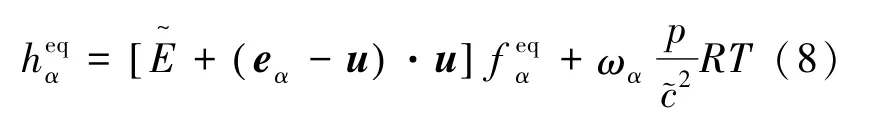
3 数值方法

前期应用Boltzmann方程可计算建模气体动理论统一算法，求解服役期满航天器解体残骸的跨流域绕流问题表明：随着飞行高度降低，解体残骸碎片再凝固形成的非规则解体物速度迅速降低，呈现近地面连续/近连续流区非规则物形激波/膨胀波多物理场复杂绕流现象［16-17］。因此，引入有限体积隐式格式求解耦合双分布函数格子Boltzmann模型方程，以保证构造的数值格式具有更好的通量守恒性以及更强的非规则解体物外形适应能力。采用有限体积法处理演化方程式（1）：

式中，

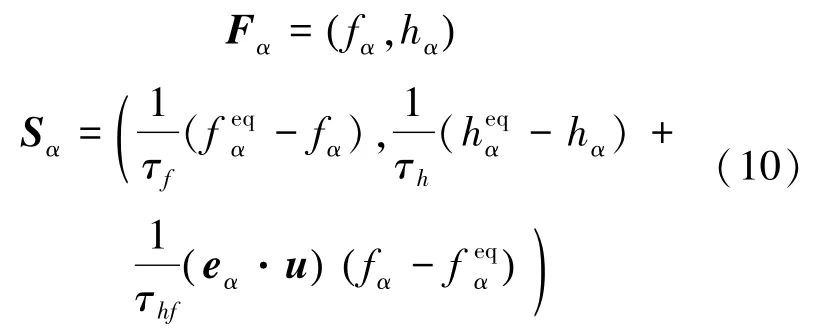
可得式（11）：

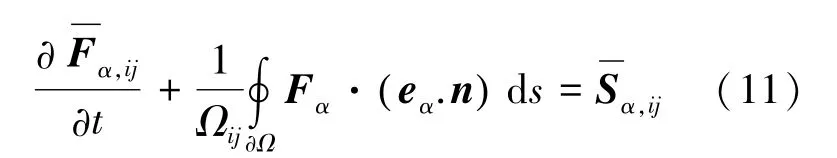
式中，Ωij为结构网格控制体 （i，j） 的体积，及表示F，S在单元控制体内的均值，n为控制体界面沿i，j增大方向的法向单位向量。本文采用NND格式来重构界面通量。因此，式（11）等号左边第二项可以改写为式（12）：

式中，Δs为控制体Ωij的边长。利用Steger-Warming流通矢量分裂，将控制体界面上的通量分解为正通量和负通量，其中正通量由计

（15）：

在时间项的处理方面，本文采用多步龙格库塔法（IMEX-RK）［6，18］。该方法采用显式方式处理对流项，采用隐式方式处理源项，具有很强的刚性问题处理能力，被成功应用于BGK模型方程的求解。分布函数从第n时间步演化到n+1时间步的公式见式（16）：

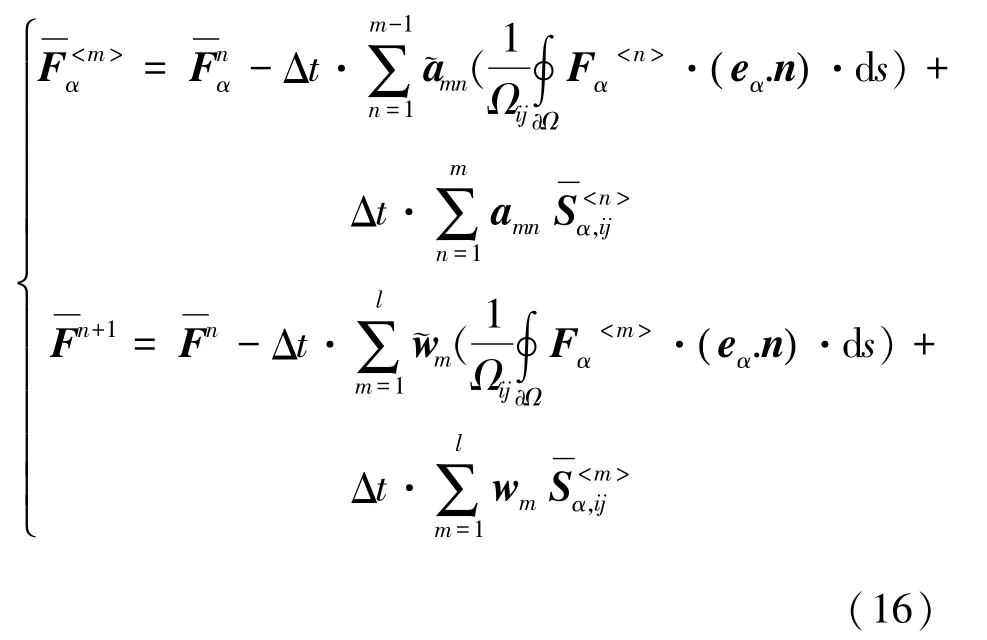
式中，上标 ＜n＞表示第n步IMEX-RK变量，l表示IMEX-RK的级数。两个l×l矩阵a~nn，ann以及l维向量w~n，wn为IMEX-RK方法的系数矩阵及系数向量。文献［19］对IMEX-RK方法的理论及各阶系数矩阵作了详细的研讨。

从式（16）可看出，第n步分布函数的计算需要第n步碰撞项的结果，其是典型的隐式格式。从演化方程式（9）可知，碰撞项包含分布函数、平衡态分布函数及碰撞松弛时间。由此可知，若能获得第n步的宏观物理量，此方程可显式计算第n步分布函数，而不用迭代。值得注意的是Boltzmann模型方程具有质量、动量及能量守恒性，即碰撞项对碰撞守恒量的矩为0。利用该性质可获得第n步的宏观物理量：针对式中的密度分布函数分量，在等式各项分别乘以碰撞守恒量φ=（1，eα）T， 并 对 所 有 离 散 速 度 点 求 和 可 得 式（17）［11］：

同理，对能量分布函数进行处理可得式（18）：

由上式可看出，第n步宏观物理量可通过前几步的分布函数显式地计算得出。有了各步的宏观量，其对应的平衡态分布函数及碰撞松弛时间即可得到。

4 算例验证与分析

采用上述方法进行Riemann问题、双马赫反射等经典问题的模拟，以验证算法程序可靠性，然后将此算法应用于翼型、方柱模型等近空间多次解体残骸碎片简化模型的亚跨超声速绕流计算。从双分布格子Boltzmann方程的构造理念可看出，特征温度的选取并不影响其还原物理量的速度分布函数矩关系。但特征温度的选取直接影响离散速度点的平衡态分布函数的插值稳定性，进而影响整个数值格式的稳定性。经验表明，特征温度的取值一般略大于流场总温。

4.1 一维Riemann问题

一维Riemann问题流场包含激波、接触间断、膨胀波3类典型的可压缩流动基本元素，流动具有解析解，并且由于流动的一维性，可方便可靠地进行边界处理，使得考核能够排除边界条件对结果的影响，被广泛用于代码考核。本数值案例中，定义参考密度ρ0=1.165 kg/m3，参考温度T0=303 K，参考粘性系数：μ0=1.86×10-5kg/( m·s)，比热比γ=1.4，普朗特数Pr=0.72，参考速度u0以及参考压力p0见式（19）：

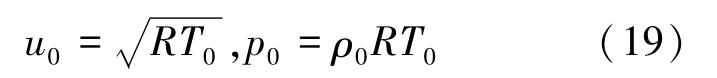
案例1：SOD问题：

其中，L0=2m，特征时间t0=L0/u0，设定特征温度Tc=2.5T0，时间步长设为d t=3000·μ0/p0，网格采用Nx×Ny=800×5的均匀网格，且d x=d y=L0/800。在x向边界处，直接指定宏观量，并由此得出边界的平衡分布函数作为边界条件；在y向，采用周期性边界条件。图1展示了在t=0.1644t0的数值计算结果及解析解的对比情况。可看出，除激波后温度场有稍许偏差外，数值结果整体与解析解吻合良好。

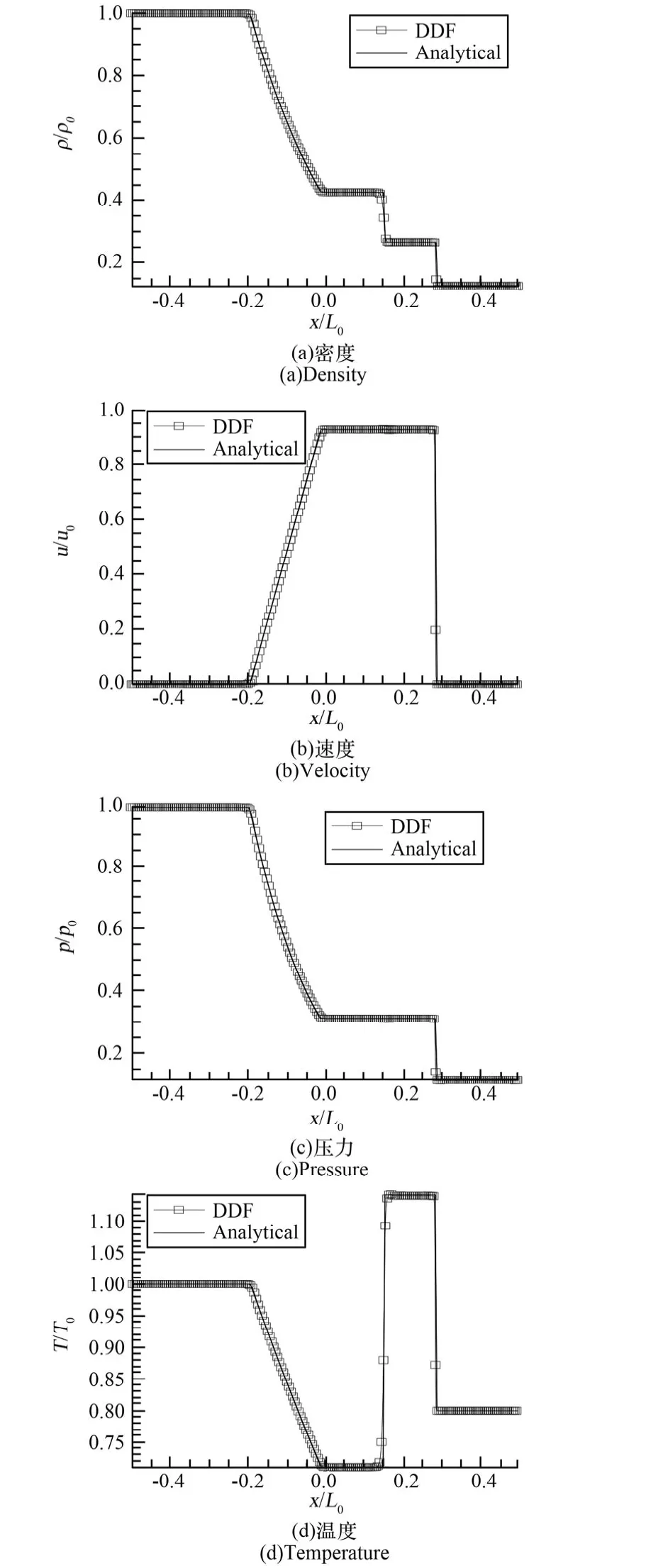
图1 SOD问题数值解验证Fig.1 Verification of numerical solution of SOD

案例2：强激波问题

这是一个典型的Colella爆炸波算例，其描述的是激波管隔膜破裂后的流动现象。由初始条件可看出，隔膜两边的压力比大于10万，对于数值方法的稳定性、空间分辨力提出了巨大挑战。本算例的基本参考物理量与上例保持一致，特征温度Tc=1000T0。图2展示了t=0.012t0的计算结果与解析解的对比情况。整体而言，计算结果与解析解吻合良好。当然，图中也可看出压力计算结果在激波后出现振荡，进一步验证发现不同的时间及空间格式会产生不同的振幅及频率，并且一定程度的加密网格可以改善振荡。密度以及温度场在激波后与解析解出现稍许的偏离，研究认为这些偏离与空间离散格式有关［11，20］。

4.2 平板双马赫反射

服役期满航天器再入解体过程高温度梯度致物面附近流动压缩气动加热积累，进入近空间连续流区多次解体残骸碎片间绕流干扰出现压缩激波反射严重的马赫杆现象，激波的马赫反射复杂流动一直是间断激波多物理场用于理论数值方法检验的典型问题。为此，计算马赫数为10的高超声速来流以30°的角度入射平面后的流场结构。本算例与一维Riemann问题数值模拟中采用的参考量保持一致。通过本算例，考核本文数值方法对二维可压缩流动适应性，其物理模型如图3所示。

计算区域为3 m×1 m的二维矩形域。反射面位于区域底面，反射面采用镜面反射边界条件，其余边界的宏观物理量根据运动激波关系式给出，密度及能量分布函数在流动入口边界给定为平衡态，在出口边界采用外推格式。计算中，特征温度Tc=85T0。图4给出t=0.062t0时刻的密度等值线及压力等值线。由图看出，计算结果清晰反映了激波马赫杆，以及第二次反射激波及马赫杆滑移线。还捕获到马赫数及斜劈角较大的情况下出现的第一马赫杆突出变形现象，马赫杆在接近壁面时逐渐垂直壁面的流动特点和理论分析吻合，与文献［21，22］进行对比分析，也可发现相互吻合较好。

图2 强激波问题数值解Fig.2 Numerical solution of strong shock

4.3 RAE2822翼型跨声速绕流问题

RAE2822翼型是典型的二维跨音速流动算例，被16个EUROVAL欧洲合作项目组和AGARD挑选为算法验证确认流动问题［23］。计算状态为Ma=0.734，α=2.79°，Re=6.5×106，采用的网格由NPARC官网提供（如图5），壁面采用非平衡外推方式实现无滑移速度边界，无穷远来流边界条件按Maxwell平衡态分布给定，出口边界条件由内流场外推，特征温度Tc=2.5T0。

图3 双马赫反射问题的物理模型Fig.3 Physicalmodel of the double-M ach-reflection

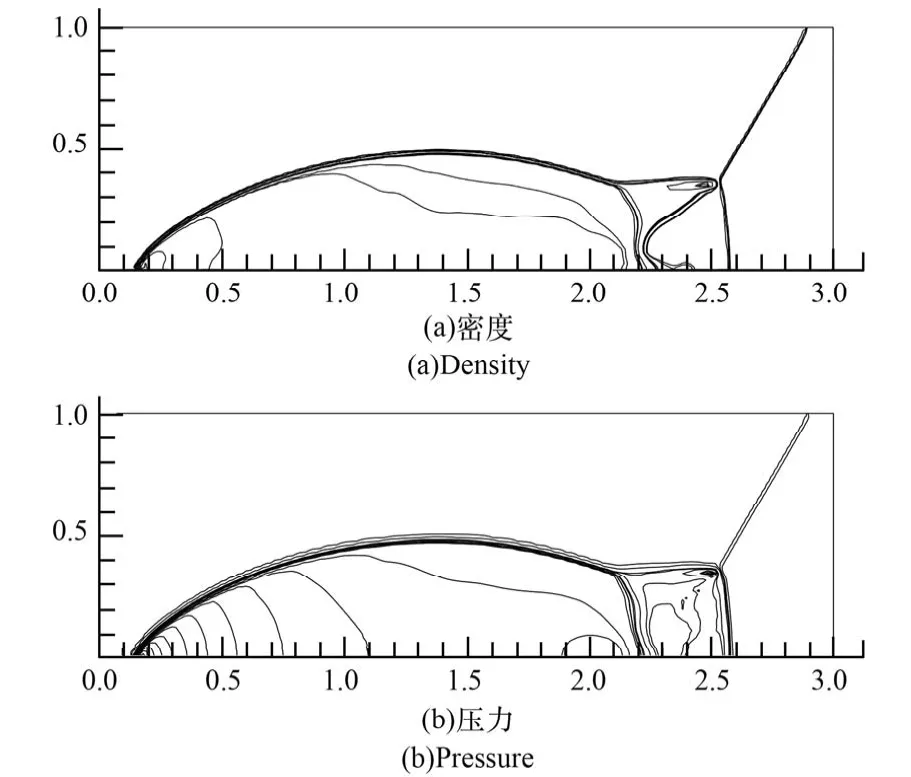
图4 双马赫反射流场密度、压力等值线Fig.4 Density and pressure contours of the double-M ach-reflection

图5 翼型绕流计算网格Fig.5 Com putationalmesh for flows around airfoil

图6绘出该翼型面绕流压力分布。可以看出，翼型背部的气流被加速后，压力逐步降低。进一步，加速形成的超声速气流经过背部激波后减速，压力陡然回升。由于图7给出了翼型表面压力系数分布及其与实验结果［24］对比情况。可以看出，除了背部湍流转捩区及激波附着区之外，其他位置计算所得压力系数与实验结果吻合较好。

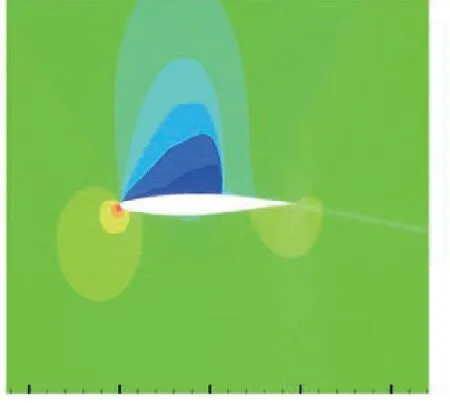
图6 翼型绕流压力等值线Fig.6 Pressure contours of the flows around airfoil

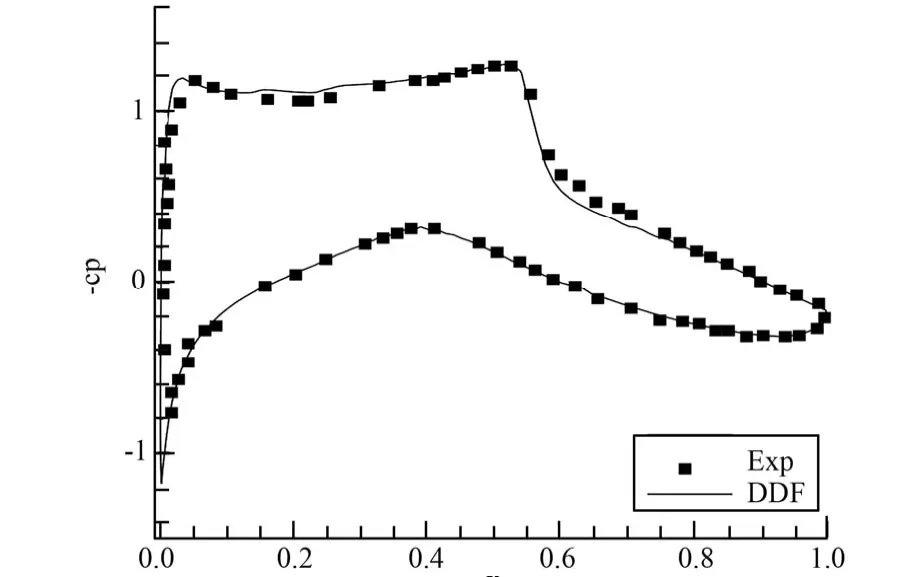
图7 表面的压力系数Fig.7 Pressure coefficient along the airfoil surface

4.4 解体残骸碎片类方柱超声速绕流问题

为考核本文算法在解体残骸碎片类方柱超声速绕流问题模拟能力，拟定二维方块在来流条件飞行高度H=50 km的大气环境下，以马赫数Ma=2.0、雷诺数Re=8×104飞行的方块绕流问题。计算中，特征温度Tc=4.5T0，无穷远处来流条件以Maxwell平衡态速度分布给定，出口条件由内流场外推，壁面边界条件采用镜面反射滑移边界条件。图8展示了本文所发展的耦合双分布函数有限体积格子Boltzmann方法的计算结果与N-S方程求解结果对比情况（“CDDF”表示耦合双分布函数有限体积格子Boltz-mann方法结果，“NS”表示NS方法计算结果）。由图可看出，绕流场密度、温度、马赫数分布与N-S方程计算结果整体吻合较好，但在温度场的尾部回流区，本文计算结果（图8（b））与N-S结果存在差异。进一步，采用等温非平衡外推无滑移边界条件计算结果的尾部回流区温度场与N-S方程求解器的计算结果吻合良好，由此说明边界条件对数值计算结果的合理性有明显影响。随着马赫数增加，气体分子速度分布函数的非平衡属性显现明显，耦合双分布函数有限体积格子Boltzmann方法的数值稳定性变差，且尾部回流区域稀薄间断粒子“真空”稀薄效应严重，会对数值稳定性产生明显影响。文献［25］研究表明，采用更复杂的离散速度模型及多松弛时间演化方程可成功实现马赫数5的前半圆柱绕流模拟，但具有回流区的高马赫绕流模拟还鲜有体现，这也反映出格子Boltzmann方法对涉及非平衡效应基于速度分布函数高阶取矩宏观量的温度、热流量模拟存在局限性。对于近空间多次解体再凝固板、方/圆柱等残骸/碎片近地面连续流，因飞行陨落速度很低，基本不存在非平衡效应，为此，本文发展经改进耦合双分布函数的有限体积格子Boltzmann方法对这类近空间连续/近连续流区残骸碎片绕流问题模拟具有较好的适应性，进一步的分析确认有待今后开展。

5 结论

本文将有限体积IMEX-RK隐式格式推广于格子Boltzmann方法，并应用在近空间连续流区非规则航天器解体物绕流模拟，结论如下：

1）采用适用于近空间连续流区残骸碎片非规则解体物绕流描述的耦合双分布函数格子Boltzmann模型，使其具有普朗特数、比热比任意可调。采用圆函数替代Maxwell平衡态分布函数，发展了离散速度模型，拓展了格子Boltzmann方法模拟高可压缩流动问题能力。

2）采用有限体积法数值离散处理该模型方程以保证构造的数值格式具有更好的通量守恒性及更强的非规则解体物外形适应能力。为了解决源项刚性问题，选用IMEX-RK格式进行时间项离散。在IMEX-RK格式应用中，利用Boltzmann方程具有的碰撞项对碰撞守恒量的矩为零的特点，推导得到了各阶宏观流动量的显式表达式，避免了隐式求解各阶速度分布函数。

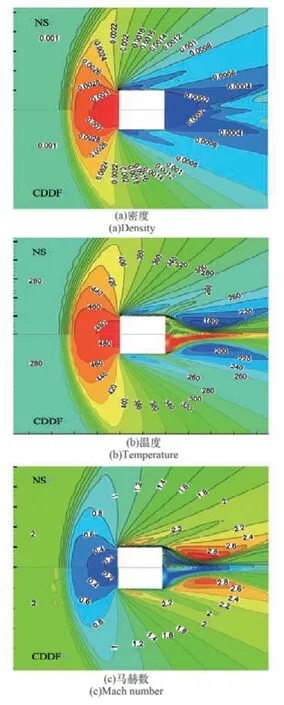
图8 CDDF与N-S方法的计算结果比较Fig.8 Solution com parison between CDDF and N-S solver

3）成功模拟了Riemann问题、双马赫反射及翼型绕流问题等案例，验证了理论模型在可压流动数值模拟能力，证实IMEX-RK能很好地解决源项刚性导致的稳定性问题。同时看出，所发展方法在模拟高马赫数复杂高温度梯度流动方面还存在不足，不同的边界条件对模拟结果的合理性、数值稳定性会产生影响。本文工作属初步研究，更精细计算分析验证有待开展。