大型航天器离轨再入气动融合结构变形失效解体落区数值预报与应用
2020-09-02李志辉彭傲平石卫波党雷宁蒋新宇唐小伟
李志辉,彭傲平,马 强,石卫波,党雷宁,梁 杰,蒋新宇,唐小伟
(1.中国空气动力研究与发展中心超高速空气动力研究所,绵阳621000;2.国家计算流力学实验室,北京100191;3.四川大学数学学院,成都610041)
1 引言
近地轨道高度300~1000 km运行的板舱桁架结构大型航天器(空间实验室、货运飞船、空间站等),服役期满或失效时,如已处于失联无控飞行状态的欧洲最大对地观测卫星ENVISAT,将面临发生可能危及其他航天航空器的碰撞、再入坠毁航迹预示、人财物安全评估、危害性分析与处置等问题[1-2]。正常情况下,这类航天器在进行返回制动后,控制系统就不再介入返回过程,在过渡段、再入段都不进行控制,与之前的再入航天器(如载人飞船返回舱)有很大区别,称无控陨落航天器,从离轨到再入过程是一个轨道高度和能量逐渐降低、连续变化过程[3]。这个过程可以划分为2个阶段:轨道衰降阶段和再入损毁阶段。在轨道衰降阶段,航天器仍然能够环绕地球、以螺旋形椭圆轨道飞行,并在稀薄空气动力、地球重力、磁场力等外力持续作用以及太阳活动的间歇性影响下,航天器的飞行轨道高度逐渐降低,轨道衰降速度越来越快;当轨道高度低于120 km时,进入再入损毁阶段[4],如图1所示,航天器在大气剧烈摩擦气动力/热作用下,摩擦生热使航天器金属(合金)桁架结构变形失效熔融,在气动热、力、减速过载等综合作用下,发生剧烈破坏解体,面临再入坠毁处置问题。

图1 大型航天器离轨再入气动/结构响应熔融解体过程示意Fig.1 Sketch of disintegration process of aerothermodynam ics/structural responsemelting for large-scale spacecraft during deorbit reentry
围绕这类航天器寿命末期离轨飞行轨道衰降与陨落再入飞行航迹预报试验[5-9],开展离轨再入空气动力学计算模型、空间环境、强气动力热环境致金属(合金)桁架结构响应变形/软化/熔融/嵌层复合材料热解烧蚀/解体相关研究,对建设与检验国家航天监测、系统跟踪、定轨预报、风险评估具有极重要意义。如中国天宫一号目标飞行器超期服役两年半后突发功能失效,无控飞行轨道衰降与再入过程中如何进行飞行航迹落区数值预报,直接依赖如何准确可靠求解再入各流域复杂多尺度非平衡条件下空气流动与传热问题;如何开展航天器金属(合金)桁架结构在超高速再入强气动力热环境变形软化、熔融毁坏非线性力学行为可计算建模,一直是流体力学、材料结构力学、计算数学与应用物理研究工作者面临的挑战[10-15]。
航天器轨道衰降与再入飞行过程,周围流场出现强烈的间断粒子稀薄非平衡流动效应,从航天器离轨飞行轨道衰降到再入解体飞行最后落区,整个陨落解体过程将从外层空间自由分子流过渡至近地面非规则解体物连续介质绕流。虽然连续流体力学和稀薄气体动力学均各有研究方法[16-18],但近连续滑移过渡区真实气体高超声速非平衡流动介于连续流与稀薄气体自由分子流之间,无论实验模拟还是理论计算均很难处理,目前尚没有统一的、准确可靠的模拟方法,急待发展相关基础理论、计算与实验模拟方法。为此,中国国家杰出青年基金项目、国家重点基础研究发展计划(973计划)项目“航天飞行器跨流域空气动力学与飞行控制关键基础问题研究(2014CB744100)”顶层设计制定了核心前沿基础研究方向“服役期满大型航天器离轨再入跨流域气动/结构响应熔融/烧蚀/解体飞行航迹预报模拟”,确立了项目核心子课题群围绕自制类天舟一号货运飞船再入大气层过程,建立跨流域气动力热一体化模拟融合弹(轨)道/结构响应计算分析方法,初步形成大型航天器跨流域气动力热/变形失效/热解烧蚀/解体飞行航迹数值预报平台框架,对接实施载人航天工程办公室针对天宫一号目标飞行器失效无控飞行再入大气层应对任务“天宫一号目标飞行器无控陨落预报及危害性分析”课题实施,分别开展服役期满大型航天器无控陨落与受控再入解体模拟研究。
本文在过去20年开展Boltzmann方程碰撞积分物理分析与可计算建模气体动理论统一算法(GKUA)[19-24]研究基础上,采用转动惯量描述气体分子自旋运动,引入能量模式配分函数和非弹性碰撞松弛数,提出求解含能量输运非平衡效应Boltzmann模型方程统一算法及其与结构热力响应有限元算法耦合模拟技术,建立适于大型航天器服役期满离轨再入跨流域气动环境与结构热力耦合响应变形/失效解体非线性力学行为一体化计算应用平台。在分析验证GKUA与DSMC、连续/近连续流区(滑移)N-S解算器、N-S/DSMC耦合算法、低密度风洞实验模拟手段途径正确性基础上,将再入气动融合结构变形失效解体算法分别应用于类天舟一号货运飞船、天宫一号/二号空间实验室再入解体数值预报,检验该算法的正确性。
2 求解含非平衡效应Boltzmann模型方程统一算法与大规模并行计算技术
基于转动松弛特性Rykov模型研究思想[25],在气体分子速度分布函数演化更新求解中考虑内自由度影响,采用转动惯量描述气体分子自旋运动,利用分子总角动量守恒作为一个新的碰撞不变量。把分子内部能量作为分布函数自变量,引入能量模式配分函数将能量在各自由度平均分布。基于气体分子速度分布函数f=f(r,V,t,e)(r、V分别是位置空间和速度空间的坐标,e为内能),在求解Boltzmann模型方程统一算法框架[19-22]下,基于权因子1和内能e对速度分布函数所依赖的速度空间进行无穷积分,引入能级约化速度分布函数f0与f1,去掉方程对内部能量连续依赖关系,确立含非平衡效应各流域统一Boltzmann模型方程,其无量纲形式为式(1):
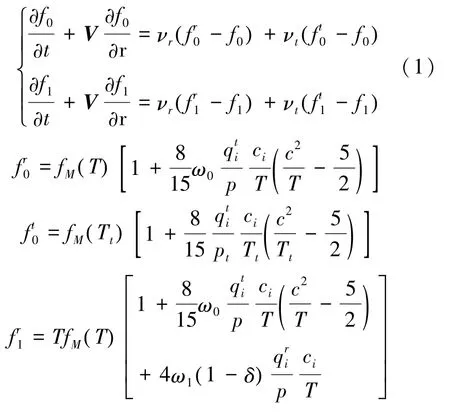

其中,上下标t、r分别表示弹性碰撞和非弹性碰撞,如νt和νr是弹性碰撞频率和非弹性碰撞频率;下标i表示空间维度方向,μ为粘性系数,n、T、p、q分别是气体分子数密度、气体流动温度、压力、热流,ω0、ω1是与气体特性相关的常数,δ对于分子间相互作用规律来说是一个常数,c是气体分子热运动速度,n是气体分子数密度。反映粘性与热传导属性的扩散时间与气体分子平均碰撞时间可分别用于描述含内能激发的多原子分子弹性与非弹性碰撞松弛变化,其统一表达式如式(2)~(3),以表征气体分子速度分布函数趋于当地平衡态分布碰撞松弛速率。

其中,B是与气体相关的常数。气体动力学各宏观流动量,如密度、流动速度、温度、压力、应力张量、热流矢量,均可通过式(4)所示气体分子速度分布函数f0和f1对速度空间积分得到。


式中,u为流动的宏观速度,其大小为u;τij为应力张量分量,δij表示i=j时其值为1、不相等时为0,i、j表示空间维度方向。
速度分布函数f0、f1对速度分量函数依赖关系属指数型。需将速度空间离散降维,去掉分布函数对速度空间的连续依赖性。在离散数值求解过程中,通过构造自适应选取的离散速度坐标点来保证离散速度坐标点确定的速度分布函数值正定守恒。为此,经过速度空间离散化处理的速度分布函数方程在计算平面内矩阵形式如式(5):

采用二阶有限差分格式[26],将时间分裂数值计算方法应用于方程(5)式中位置空间的三个对流运动方程和碰撞松弛源项方程,进行耦合迭代数值求解,构造在每个离散速度坐标点处直接求解分子速度分布函数演化更新的气体动理论统一数值格式如式(6):

式中,L为对应方向上的算符,n表示n时刻的值,下标S表示源项。对于(6)式,采用二阶Runge-Kutta方法数值求解具有非线性源项的碰撞松弛方程;采用时间和位置空间均为二阶精度基于原始变量(即相对于f0σ,δ,θ、f1σ,δ,θ)的NND-4(a)预测-校正两步差分格式[26]数值离散对流运动方程。
针对显式格式差分求解离散速度分布函数,计算时间步长受显式格式稳定性条件制约[27],为提高计算大型航天器再入解体过程非规则物形绕流计算效率,发展了Boltzmann模型方程隐式格式求解方法[28]。为方便起见,以一维Boltzmann模型方程为例构造隐式格式,简单记为式(7):


式中,A=∂F/∂U相应于Boltzmann模型方程对流输运项的Jacobi矩阵,M=∂S/∂U相应于Boltzmann模型方程碰撞松弛源项线性化矩阵。为此,求解过程可分解为:①令(8a)右端第二项为零或取前一次迭代值,利用左边的边界条件由左向右扫描,依次求出;②将上一步求出的代入(8b)右端,利用右边的边界条件,从右向左进行扫描,求出;③以上左右各扫描依次完成一次迭代,将每次迭代求出的新值代入(8a)式右端并重复扫描,直到小于给定的某个值为止。一般只需进行两次迭代就可满足精度要求。由(8)式可看出前的系数为标量形式,计算过程不需块矩阵求逆运算,计算实现较简便。
根据数值格式(8),建立了考虑非平衡效应、基于分子速度分布函数特征化表征的基础边界条件的数学模型及数值处理方法[25,30],一旦所有离散速度坐标点处的速度分布函数被数值求解,则任一时刻物理空间各点的宏观流动量如气体密度、流动速度、温度、应力张量和热流矢量等,便可通过速度分布函数乘以分子速度的某种函数形式再对离散速度空间数值积分而被演化更新。
适于航天再入气动力热问题的Boltzmann方程可计算建模气体动理论统一算法,计算空间是由离散速度空间和位置空间组成的六维空间,并考虑内部能级分布,形成多相空间。从区域分解并行化原理出发,可将算法求解空间划分为位置空间分解策略、速度空间分解策略。通过对各阶段算法过程进行变量依赖关系分析看出,在各个离散速度坐标点 (Vxσ,Vyδ,Vzθ)处数值求解离散速度分布函数的差分格式中,位置空间Ωr各维方向都存在数据相关性,离散速度子空间ΩV各维方向则毫无数据相关。使用离散速度数值积分法对气体分子离散速度分布函数进行矩积分确定飞行器绕流宏观流动量的过程,在位置空间Ωr各维方向都不存在数据相关性,在离散速度空间ΩV各维方向以归约形式体现了问题的相关性。因此,对于ΩV分解策略,计算宏观流动量需要在ΩV内进行并行归约计算,会产生数据通信。依据二叉树方式并行归约,可得单进程处理的数据量CV如式(9):
式中,假设位置空间Ωr是NiNjNk网格阵列,处理器阵列为NpσNpδNpθ。通常可将 ΩV按三维方式等分分解:为了分析离散速度空间的网格阵列与处理器阵列的分布关系,将式(9)改写为式(10):

式中,V=NσNδNθNiNjNk,Nσ、Nδ、Nθ分别为3个计算方向离散速度点数。从式(10)看出,为获得较小CV值,通常设置Npσ≤Nσ、Npδ≤Nδ、Npθ≤Nθ为宜。因此,基于离散速度空间ΩV并行分解策略能实现具有成千上万CPU核甚至更大规模并行计算。将求解Boltzmann模型方程并行算法计算效率与宾西尼亚大学依靠高性能计算机开展求解BGK模型方程不同马赫数一维激波结构演化问题的研究[31]进行比较,表1给出了本文基于256个CPU的GKUA并行算法用于计算三维绕流问题的并行加速比与文献[20]BGK方程计算一维激波的并行加速比。可见,GKUA三维绕流并行计算加速比与文献[31]一维BGK方程并行计算加速比相当,显示出统一算法卓越的并行加速性能,是国际首创的求解各流域三维复杂绕流问题的气体动理论高性能并行算法,且具有良好的并行可扩展性与并行效率。

表1 基于256CPU统一算法并行计算加速比与国际同行比较Table 1 Comparison of speedup ratio of parallel computation for GKUA on 256CPU w ith sim ilar international studies
图2绘出本文GKUA程序经异构协同模式并行移植优化得到500~45000处理器核的并行计算加速比与并行效率,图中横坐标表示计算所用进程数。可看出,本文设计的适于众核异构计算机的气体动理论高性能并行算法加速比,仍属拟线性加速比,并行效率80%以上,良好的并行加速性能足以保证在较高并行效率下,通过增加处理机数,即可大大增加计算规模,使航天领域依靠传统计算条件难以解决从高稀薄自由分子流到连续流全飞行流域复杂高超声速绕流问题计算求解变为现实成为可能。
3 建立结构动态热力耦合响应变形行为有限元计算方法

图2 统一算法在500~45000多核处理器进程并行计算加速比与并行效率Fig.2 Speedup ratio and parallel efficiency on 500~45000 processors for gas-kinetic parallel algorithm
直接求解Boltzmann模型方程统一算法基于气体分子速度分布函数演化更新,使用(4)式数值积分得到所有宏观流动物理量的做法,能准确捕捉物面不同位置的力、热流、温度、速度分布,这为进一步研究飞行器在极高速再入强气动力热环境下,其部件结构内部热传导致温度梯度与弹塑性位移变形行为创造了条件。为研究航天器再入气动力热环境致结构变形/失效解体非线性力学响应行为,基于瞬态热传导方程与材料热弹性动力学方程,需构造动态热力耦合响应数学模型,建立再入强气动力热环境致材料结构热力响应行为有限元算法。
设在空间区域Ω⊂R3中,不考虑阻尼影响,材料热弹性动力学方程可表示为式(11)[32]:


式中,c表示材料比热,kij为材料热传导张量,h为热源项。利用变分原理推导[13,33-34]关于u与θ的动态热力耦合控制方程的弱形式如式(13):

该耦合弱形式属于双曲抛物耦合系统,其温度场与位移场相互依赖,在有限元计算过程中两方程需要联立求解。
对于热弹性动力学方程,使用Newmark隐式方法实施热弹性动力学方程时间上的离散推进,计算速度与位移[13,34];使用高精度Crank-Nicolson格式[13,35-36]耦合求解热传导方程。
4 高超声速再入气动环境致结构变形/失效非线性力学行为一体化模拟
为了准确可靠模拟航天器再入中高超声速气动力/热环境致金属(合金)桁架结构材料内部温度分布与响应变形、热损毁等非线性力学行为,需要将动态热力耦合响应有限元计算方法(FEM)与求解Boltzmann模型方程气体动理论统一算法(GKUA)相结合,发展一体化耦合模拟技术。为简单起见,这里以图3所示再入竖直平板含碳钢结构绕流模型为例,把任一时刻GKUA得到的气动热与气动力代入结构热力耦合响应计算公式,作为有限元计算的边界条件。对图3所示钢板厚度0.015 m、高度0.5 m,钢板外部受再入近连续稀薄过渡流区高超声速绕流冲击,来流克努森数Kn∞=0.01、马赫数Ma∞=8.366 6、γ=1.4。使用统一算法求解外流场,因高超声速再入近连续过渡流,在竖直钢板附近绕流场形成较厚的脱体激波层(如图3(a)),钢板表面受到强气动热与气动力作用,在迎风区承受高温与高压,若不考虑钢板振动,根据GKUA求解获得钢板表面温度与压力作为材料结构动态热力耦合响应有限元算法界面条件,对钢板内部温度分布与变形情况进行计算分析。
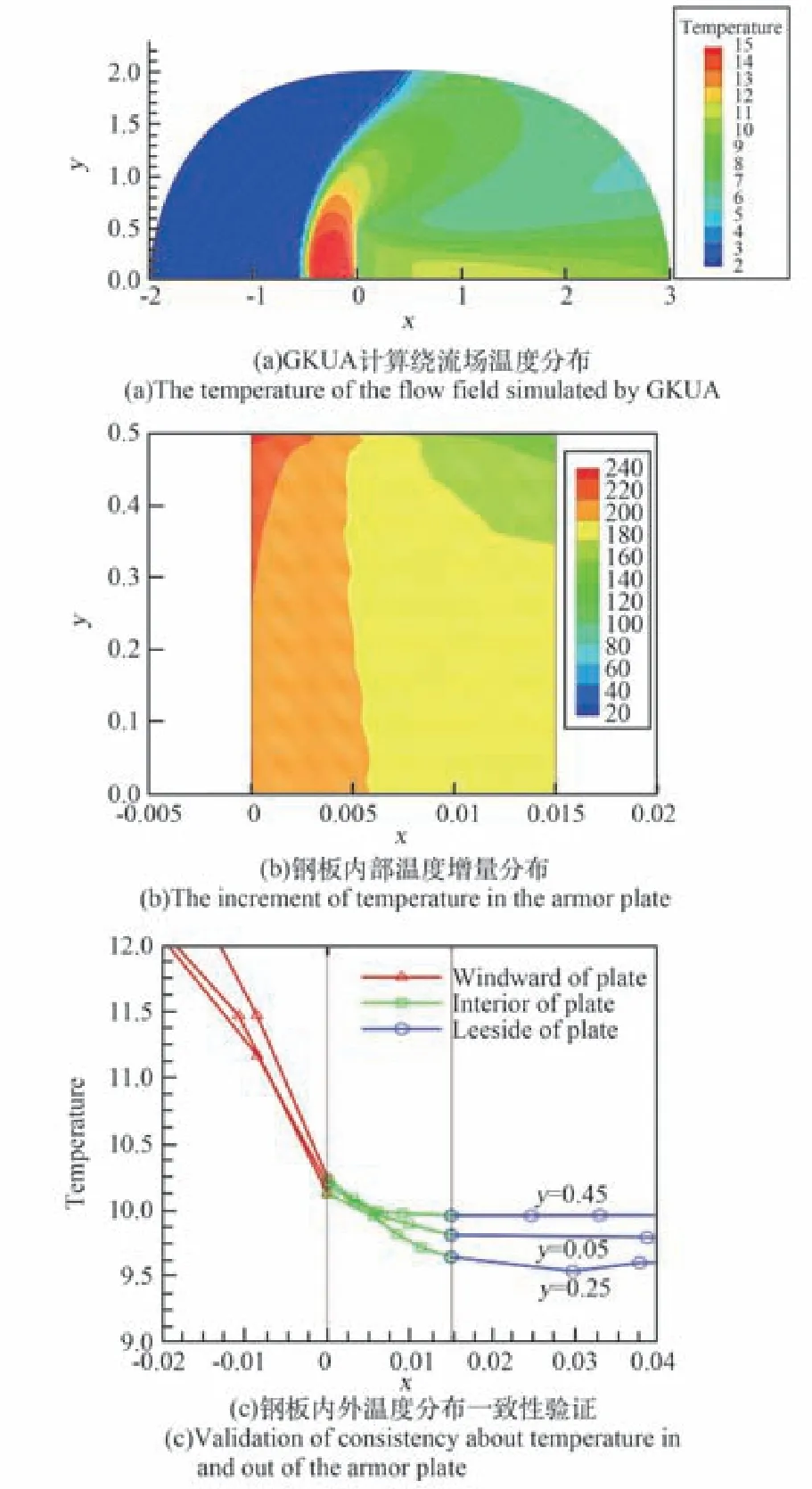
图3 高超声速再入Kn∞=0.01、Ma∞=8.366 6竖直钢板绕流场温度等值线GKUA与内部温度分布FEM计算验证Fig.3 Tem perature contours and computation verification of GKUA and FEM along x axis between flow field and inner structure under hypersonic reentry when Kn∞=0.01,Ma∞=8.366 6
对钢板截面内部结构进行网格剖分,固定钢板下表面(y=0)。由于用于绕流物体外部流场计算的网格与用于热力耦合响应计算的钢板内部结构网格的不一致性,这里将GKUA计算得到的外部流场网格边界的温度与压力进行线性插值施加到钢板内部网格边界中。假设钢板处于初始温度T0,外部流场处于稳定状态,钢板外表面温度达到T=T0+θ,其中T为GKUA计算竖直钢板外流场稳定时获得的温度值,由此得到钢板物面边界的温度增量值θ=T-T0。
在外部流场计算中,为表征飞行器再入不同高度的跨流域绕流多尺度效应,通常采用无量纲模型化计算;而在物体内部结构场的热力耦合有限元计算中,则需将其转换成符合实际的有量纲温度与压力。如在流场中计算得到的温度与压力值分别为T*与p*,则实际温度与压力T与P分别为T=T*T∞、P=p*ρ∞V2∞。其中,T∞、ρ∞、V∞分别为参考温度、来流密度与来流速度。作为算例,钢板物性参数为E=2.06×1011Pa,ν=0.3,α=1.5×10-6/℃,ρ=7 850 kg/m3,cv=460 J/(kg·℃),k=50W/(m·℃)。初始参考温度T0=500℃,取时间步长Δt=0.05 s,计算时间为5 s。图3(b)绘出直接耦合法计算得到钢板内部结构场温度增量分布等值线云图,图3(c)绘出钢板不同部位y=0.06、0.26、0.46外部流场与内部温度场沿x方向变化曲线。可看出,钢板外部使用GKUA计算得到的迎风面y=0.06、0.26、0.46处温度与背风面温度,均分别与钢板内部热力耦合有限元计算得到的钢板表面温度吻合一致,证实外流场求解Boltzmann模型方程统一算法与材料内部动态热力响应耦合算法模型与程序设计实现的正确可靠性;物体内部靠近钢板迎风面驻点(坐标原点)的温度较附近其他点的温度高,最高的温度点则出现在钢板的左上拐点,此处边界曲率变化最大,流场热流在此达到最大,由稳态热传导方程极大值原理可知,材料内部温度在此也达到最大,故在钢板迎风边界由下到上温度出现一个先降后升的变化,这种变化在材料内部也清楚地反映出来。
图4绘出钢板在高超声速再入绕流环境受外部温度与压力双重作用下t=1~5 s整体变形情况,可以看出,在受外部高超声速强气动力热绕流迎风面与背风面较大温度与压力差双重作用下,钢板首先产生了较大幅度的弯曲(图4(a)),这是迎风面压力作用的结果,随后气动热使得钢板内部温度逐渐升高,在钢板内部形成了非均匀热应力分布,高温使得钢板在迎风面产生较背风面更大的热膨胀,所产生的热应力方向与迎风面压力方向相反,内外两种力相互作用使得钢板弯曲幅度变得相比于计算初始阶段的弯曲幅度更小,在5 s时,钢板内部温度分布还未稳定,所以热膨胀仍在持续,即5 s时钢板的弯曲变形还将继续,最终达到图4(d)的稳态变形分布。

图4 强气动力热环境致竖直平板不同时刻及稳态变形图(变形放大尺度为50倍)Fig.4 Time history of plate deformation computed by FEM,displacement am plified by 50 times
5 航天器陨落再入过程跨流域气动环境与结构热力响应变形计算分析
5.1 求解Boltzmann模型方程统一算法对大型航天器跨流域气动并行计算检验
为确认求解Boltzmann模型方程统一算法对大型航天器陨落再入过程跨流域气动并行计算的精度和可靠性,对长度Lref=10.409 m、最大直径Dref=3.452 m的类天宫飞行器两舱体近连续过渡流区两个绕流状态H=65.2 km、Ma∞=12.5、Kn∞=5.1×10-5(case1)与H=62.1 km、Ma∞=12.79、Kn∞=3.37×10-5(case2),在流动介质氮气(N2),迎角 α=2°、0o、2°、5o、10o、15o、20o、25o,取Pr=0.72、γ=1.4、Tw=300 K,分别开展GKUA与DSMC[37]、N-S/DSMC[17]、N-S方程计算和低密度风洞实验测试结果间比较分析。图5绘出GKUA采用4096CPU核并行计算得到的两舱体陨落再入case1绕流场压力、流线结构、俯仰力矩、压心位置与DSMC、N-S/DSMC、滑移N-S(NS-Slip)、无滑移N-S(NS-NoSlip)、低密度风洞实验(Exp.)结果比较曲线,可看出,对纵横十数米大尺度复杂结构航天器,即使在较高飞行高度,但因极低的来流克努森数Kn∞=5.1×10-5,流场整体上呈现明晰的脱体激波、膨胀真空区与尾部流动分离的连续流区绕流面貌,因前体对接台复杂结构,气体绕流出现高压、高温区,在跨越前台区进入背风圆柱面及尾部呈现较低密度、压力分布;且前体对接台、后体非规则处,稀薄气体速度滑移效应表现严重,有迎角绕流出现迎风区与背风区物面流线汇聚,25°迎角绕流前后舱体上部均出现流线分离、非对称涡结构,图5(a)、(b)分别揭示了大型复杂结构航天器绕流特殊的连续流、近连续滑移、稀薄效应共存混合流动输运现象及变化特点。图5(c)、(d)分别绘出类天宫两舱体陨落再入case1绕流状态不同迎角俯仰力矩和压心位置验证比较情况,可看出,对case1(模拟高度H=65.2 km)的俯仰力矩,N-S方程及滑移N-S计算与其他方法计算结果均相差较大,说明该状态下稀薄效应较为明显,N-S方程已不再适用,而统一算法(GKUA)计算结果始终介于N-S/DSMC、DSMC和N-S方程所得结果之间,且更吻合于DSMC结果,误差在合理范围内,同时统一算法所得压心位置较DSMC、N-S/DSMC与实验值符合更好,表明统一算法结果更为准确可靠。

图5 类天宫两舱体H=65.2 km、Kn∞=5.1×10-5、Ma∞=12.5、α=25°流场及气动力系数计算与实验比较验证Fig.5 Validation of computation and experiment for aerodynam ics on two-capsule vehicle of Tiangong type spacecraft w ith H=65.2 km,Kn∞=5.1×10-5,Ma∞=12.5 andα=25°
图6绘出case2绕流状态计算与实验比较情况,由于飞行高度H=62.1 km更低,属于来流Knudsen数Kn∞=3.37×10-5更小的连续流区,整体而言N-S方程计算所得结果与实验值符合较好,其他几种方法均有所偏离实验值,但误差均在5%以内。同时可看出统一算法结果与N-S方程结果吻合,表明统一算法对连续流区计算具备良好的适应性,计算结果准确可靠。几种空气动力学模拟手段对大型复杂结构航天器case1、case2绕流状态模拟的分析比较表明,统一算法对更高稀薄效应H=65.2 km计算结果与DSMC、N-S/DSMC及实验吻合更好,对更低飞行高度H=62.1 km计算与N-S方程及实验符合较好,证实从H=65.2 km到H=62.1 km这样的飞行高度段,大型航天器绕流流态从稀薄流到连续流发生明显变化,而统一算法在跨流域气动计算所具有的一致收敛性优势。
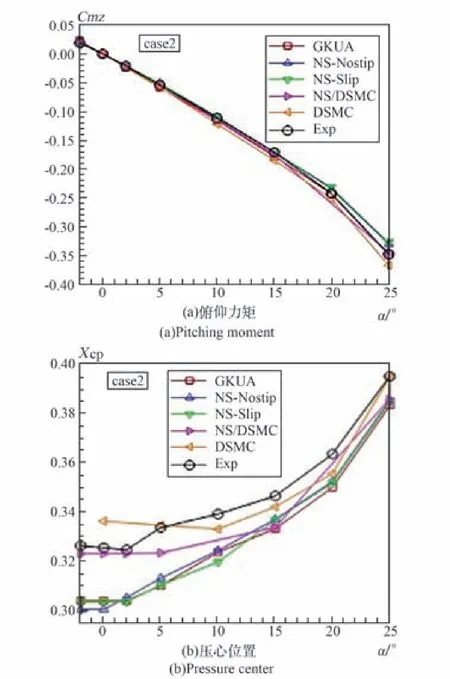
图6 类天宫两舱体H=62.1 km、Kn∞=3.37×10-5、Ma∞=12.79气动力系数计算与实验比较验证Fig.6 Validation of com putation and experiment for aerodynam ics on two-capsule vehicle of Tiangong type spacecraft w ith H=62.1 km,Kn∞=3.37×10-5 and Ma∞=12.79
5.2 类天宫飞行器陨落再入过程跨流域气动环境与结构热力响应计算分析
依靠跨流域空气动力学模拟方法计算得到类天宫飞行器陨落再入飞行绕流物面压力、热流分布,使用第4节介绍的气动环境与结构变形/失效解体非线性力学行为一体化模拟手段,就可实时计算得到结构温度增量与位移变形,图7(a)、(b)分别绘出类天宫飞行器陨落至H=120 km、110 km时的物面结构温度等值线云图,说明大型复杂结构航天器陨落至120 km高度时,因超高速气流在物面附近强扰动,致太阳电池翼与对接台肩部区域出现高温区;随着高度进一步降低,陨落至110 km,大气密度增加,高超声速气流在飞行器前部形成脱体激波层,冲击在靠近安装支架的太阳电池翼面,形成更为强烈的高温区,并与激波过渡带对太阳电池翼面力热冲击形成双重耦合作用,致太阳电池翼因结构的动态响应而变形弯曲,图7(c)绘出结构动态热力耦合响应有限元算法模拟该类天宫飞行器无控陨落至H=100 km、V∞=7.6 km/s强气动力热环境致结构整体稳态变形情况,计算表明强气动力热作用致太阳电池翼安装支架变形达2 m,超过支架屈服强度,帆板联接机构将失效、折断损毁。
类天宫飞行器首次解体后两舱体经空气动力配平绕流陨落过程,将持续在外部流场气动力/热作用下,物面温度不断升高。图8(a)、(b)分别绘出两舱体陨落至H=90 km、α=0°与α=20°飞行绕流物面温度分布,可看出,α=0°时,物面最高温度在对接口达到1450 K,而α=20°时,物面最高温度同时出现在对接口与前台迎风面,达到1550 K。图8(c)绘出类天宫飞行器两舱体分别以α=0°与α=20°陨落H=120~90 km的过程中物面最高温度随飞行高度降低非线性增加的曲线,从图中可以看出,当飞行器陨落至100 km左右,考虑与不考虑辐射效应计算得到的结构热力响应温度分布产生严重偏离,热辐射开始在热传输中产生显著影响;当陨落飞行至90 km,两舱体结构在0°迎角时驻点温度达到1500℃左右,在20°迎角时两舱体结构最高温度超过1500℃,而且辐射效应引起的物面温度计算偏差高达数百℃。这说明开展大型航天器陨落再入过程中因强气动力热环境和辐射传热耦合而导致结构热力响应变形/失效解体的有限元计算研究是一个新的研究方向。

图7 类天宫飞行器H=120~100 km、V∞=7.6 km/s强气动力热环境致结构温度变化和稳态变形Fig.7 T Temperature distribution and steady state deformation of structure at H=120~100 km and V∞=7.6 km/s around Tiangong type spacecraft by strong aerodynam ic heating
6 服役期满航天器离轨再入解体数值预报平台研制与应用
针对非回收类航天器服役期满离轨陨落回归地球大气层过程,遍历外层空间到地面全飞行流域,单凭任何一种空气动力学模拟手段难以胜任。作为跨流域空气动力学模拟方法集成升华对接工程需求与应用,构建了Boltzmann方程可计算建模气体动理论统一算法、DSMC、N-S/DSMC、(滑移)N-S解算器、低密度风洞实验测试多种空气动力学模拟手段[15,17,37]验证结合,可靠模拟大型航天器从轨道衰降到再入跨流域空气动力学一体化模拟平台。以此为基础,结合发展气动热环境与结构传热/复合材料热解烧蚀计算方法[9]、航天器解体分离、多体绕流数值模拟方法[28]与数据库、软件工程手段,建立以运动弹道计算为主线,融合气动力、气动热、金属桁架结构热力响应变形失效/软化融熔、复合材料热解/烧蚀及再入解体(部件级或碎片级)飞行航迹联合计算分析机制。结合外测轨道信息,研制服役期满航天器离轨陨落飞行轨道衰降与再入跨流域气动/结构响应变形失效/烧蚀/解体数值预报模拟系统应用平台[5,8,13,14,18,28,33]。
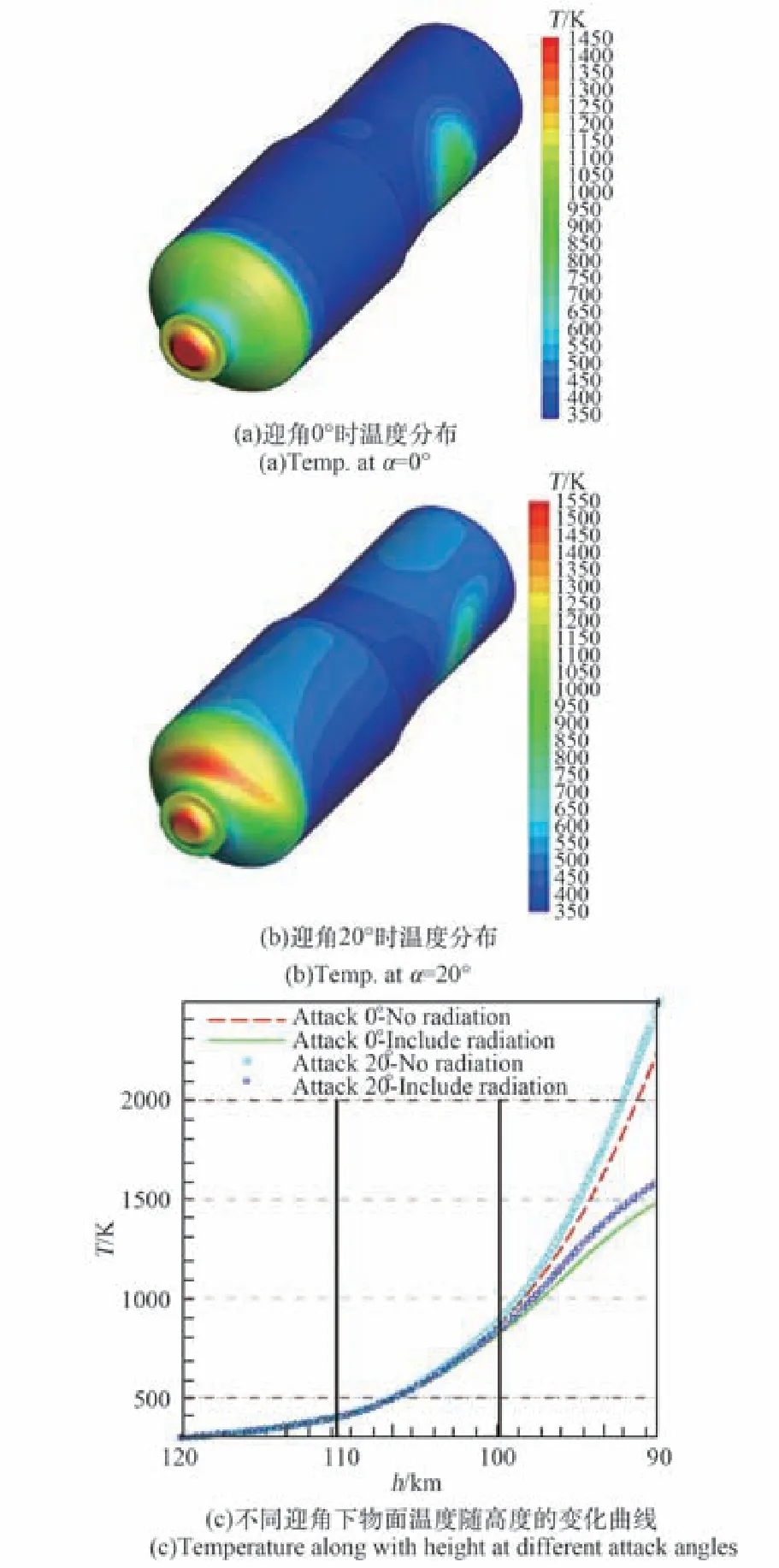
图8 类天宫飞行器两舱体陨落H=120~90 km强气动力热环境致结构温度变化分布Fig.8 Tem perature distribution in structure during the reentry of H=120~100 km around Tiangong type two-capsule spacecraft by strong aerodynam ic heating
6.1 类天舟一号货运飞船受控再入解体数值预报应用检验
以自制类天舟一号货运飞船模型为试验验证对象,实施运行轨道自由分子流到再入解体近空间连续流各流域飞行绕流模拟预报,图9绘出类天舟一号货运飞船受控离轨再入341.2~100.9 km时飞行的绕流压力分布与航迹预报结果。数值预报模拟表明,类天舟一号再入飞行高度115 km以上,气动载荷不会使太阳电池翼结构损坏;到110 km时,气动载荷作用,帆板结构有可能会损坏;100 km以下,气动载荷作用急剧增大,帆板结构损坏,判断发生首次解体高度在101.3~100.9 km太阳电池翼撕裂分离。随后,类天舟一号两舱体陨落飞行至90 km高度,头部对接机构16 mm后退量;87~85 km实验舱段后退量10mm烧穿毁坏。由此判断类天舟一号发生二次解体高度90~87 km两舱体实验舱外壳熔融所致,此时中继天线断裂抛出、天舟一号与地面通信中断,这与实际再入遥测信号消失点88.75 km吻合,偏差1.41%。其后,因天舟一号实验舱外壳被烧穿,舱内容器或蓄电池模组爆炸可致部件级与碎片级多次解体。
6.2 天宫一号目标飞行器无控再入解体落区数值预报
针对天宫一号目标飞行器超期服役两年半至2016年3月16日突发功能失效进入无控飞行轨道衰降,利用航天测站雷达成像、光学自适应图像数据等,建立非合作外测估计天宫一号空间飞行姿态测量手段,实施二维成像三维重构空间飞行姿态及帆板姿态角识别,建立天宫一号空间飞行姿态估计方法,解决天宫一号飞行姿态联测输入气动模拟的条件问题,结合外测轨道星历数据,对沿轨道衰降飞行的天宫一号空气动力三力(阻力、升力、侧力)三矩(俯仰力矩、偏航力矩、滚转力矩)开展大规模并行计算,并基于数值结果优化修正当地化桥函数关联参数快速计算方法,融合弹(轨)道后实施高精度迭代计算。
根据2018年4月1日天宫一号外测姿态数据与2018年4月2日6时22分外测轨道星历数据,使用系统各执行模块组成的模拟平台[18]数值预报:天宫一号于北京时间2018年4月2日7时54分41秒到达120 km再入大气层,再入速度7492.13 m/s;首次解体高度:110~105 km(帆板链接框架断裂),二次解体高度:资源舱小头朝前飞行至100~95 km,中继天线于97.5 km从资源舱飞出至95 km解体,主承力锥台、轨控发动机83~56 km解体,未存留大的残骸,多次解体残骸碎片散布核心区纵向长约1200 km、横向宽约100 km,图10(a)绘出天宫一号陨落再入解体残骸碎片落区数值预报结果与美国航空航天官方网站后续标注的天宫一号再入事后监测图10(b)所示吻合一致,且落区数值预报结果和事后一天美国联合太空作战中心公布的图10(c)所示的天宫一号坠落南太平洋海域极为相容,与美国太空司令部事后确认没有大型残骸落地的监测数据吻合很好,所建立的气动融合结构/弹(轨)道再入解体数值预报算法模型的正确性与预报精度得到了检验。且分析表明,数值预报大型航天器绕地球一圈用时一刻钟;停止姿态、外测轨道数据供给,6 h后地心惯性系位置矢量预报偏差2.3 km,这就开辟了大型航天器无控再入解体落区数值预报新领域发展方向。

图9 类天舟一号货运飞船离轨再入341.2~100.9 km解体飞行绕流压力分布与航迹预报模拟结果Fig.9 Pressure distribution and track forecast simulation of Tianzhou-1-type cargo spacecraft during the reentry of 341.2~100.9 km
6.3 天宫二号空间实验室受控再入解体落区数值预报
2019 年在前期研制天宫一号无控飞行轨降再入解体数值预报平台基础上,实施了天宫二号超期服役近一年后受控再入解体回归地球大气层过程,在2019年7月16日北京航天飞行控制中心提供的天宫二号第二次变轨制动发动机关机后的倒飞理论设计弹道参数基础上,于7月18日18:00数值预报:天宫二号首次解体高度105~103 km(帆板链接框架断裂);二次解体高度95~92 km,中继天线熔融解体高度95 km之后和地面通信中断,与2019年7月19日晚天宫二号实际再入遥测信号消失点94.775 km吻合一致,偏差0.24%;多次解体残骸碎片核心散布区域:南太平洋偏东南海域起点西经132.4°、南纬35.2°,终点西经126.7°、南纬37.5°,长约570 km,宽约100 km,较预定海域6000 km×1700 km,减小170余倍,证实数值预报模型能提前锁定大型航天器受控再入解体残骸碎片落区散布范围,图11(a)绘出天宫二号受控再入解体落区数值预报与轨道外推理论设计预定海域比较验证情况。随后为了进一步复核验证该数值预报模型对大型航天器受控再入解体残骸碎片落区散布范围模拟结果正确性,在载人航天工程办公室、北京航天飞行控制中心建议下,由北京中心轨道室提供天宫二号于2019年7月19日20:33第二次变轨制动发动机关机220~100 km实际再入飞行参数,使用数值预报模型开展复核复算,验证了图11(b)和(c)所示为天宫二号二次解体中继天线毁坏通信中断与天宫二号实际再入遥测信号消失点及数值预报复核复算落区与预定海域对照结果,证实数值预报弹道与天宫二号实测GPS弹道偏差为数米量级。

图10 天宫一号无控飞行轨降再入解体落区数值预报结果与美国航空航天、太空司令部事后监测图示吻合一致Fig.10 The present numerical forecast of uncontrolled reentry disintegration of Tiangong-1 was in good accordancew ith the USA monitoring plot of the falling area
7 结论
1)针对大型航天器服役期满离轨再入坠毁飞行航迹数值预报问题,基于Boltzmann方程碰撞积分物理分析与可计算建模,建立了含非平衡效应各流域统一Boltzmann模型方程及隐式混合通量数值格式与稳定运行数千数万CPU核大型航天器陨落再入跨流域气动力热绕流环境大规模可扩展并行算法,具有500~45000处理器核拟线性并行计算加速比与80%以上高性能并行计算效率。

图11 天宫二号受控再入解体落区数值预报与实际再入遥测信号消失点、理论设计预定海域比较验证Fig.11 Com parison and verification of the present numerical forecast,the actual reentry telemetry signal vanishing point,and the theoretical design of predeterm ined sea area for the controlled reentry of Tiangong-2
2)通过将求解Boltzmann模型方程统一算法对类天宫飞行器两舱体跨流域气动并行计算与DSMC、N-S/DSMC、N-S解算器、低密度风洞实验测试结果间的比较分析,证实GKUA求解大型复杂结构航天器陨落再入解体过程跨流域高超声速气动问题精度与可靠性,揭示了大尺度非规则物形绕流多流区共存混合流动输运现象与变化特点。
3)利用Newmark隐式方法设计热弹性动力学方程时间上的离散推进,计算速度与位移;使用高精度Crank-Nicolson格式求解热传导方程,建立了适于航天器再入强气动力热环境致结构响应变形行为隐式有限元算法。通过开展求解Boltzmann模型方程统一算法对竖直平板、类天宫飞行器高超声速流场计算与结构力-热耦合响应变形毁坏非线性行为一体化模拟检验,证实所提出服役期满航天器陨落再入跨流域气动环境与结构响应变形/失效解体一体化算法可靠性,揭示了航天器陨落再入高超声速绕流强气动力热冲击致物面材料内部温度分布与结构变形失效非定常演化机制。
4)通过研制服役期满大型航天器离轨再入跨流域气动融合结构响应变形失效/烧蚀/解体数值预报模拟系统应用平台,对自制类天舟一号货运飞船模型进行了数值预报,与实测数据对比表明所建立气动融合结构/轨道衰降与再入解体落区数值预报模型算法正确性与高精度预报能力。对天宫二号空间实验室受控再入解体过程气动融合结构/弹道数值预报表明,数值预报模型能提前锁定大型航天器受控再入解体残骸碎片落区散布范围。
5)天宫一号无控飞行与天宫二号受控再入解体落区数值预报比较分析表明,受控再入弹道倾角很大,如天宫二号较天宫一号无控再入的弹道倾角大13.5倍,致再入飞行距离、时间上天宫二号较天宫一号缩短近四倍,其残骸/碎片核心落区散布范围较无控再入解体落区范围小若干倍,可根据残骸碎片预定安全落区反演设计受控离轨控制策略,预期可大大缩小预定安全海域,如前期对外公布的天宫二号预定海域(西经160~90°、南纬30~45°)6000 km×1700 km,而实际数值预报天宫二号再入解体落区散布区域(西经132.4~126.7°、南纬35.2~37.5°)570 km×100 km,较预定区域小170多倍。数值预报模拟平台可提前较长时间预报锁定服役期满大型航天器受控再入解体残骸碎片落区散布范围。
本文是阶段性工作,搭建了服役期满大型航天器离轨再入强气动力热环境致结构热力响应变形失效解体数值预报模型算法及无控轨降与受控再入解体数值预报应用平台框架,下一步拟研究材料变形熔融分子动力学可计算建模与热力响应有限元算法、统一算法耦合杂交实时模拟,有望在提高服役期满大型航天器再入解体数值预报精度方面取得更大突破。
