基于用户异质性的旅游巴士定价研究

李妍峰，龚桂琳

(1.西南交通大学 经济管理学院；2.服务科学与创新四川省重点实验室，四川 成都 610031)

随着人们收入的大幅度提高及旅游业的快速发展，国内游客人数呈现出快速增长的趋势，使得旅游交通的出行需求越来越大。旅游公共交通作为旅游业的重要组成部分，若其发展滞后，会成为该城市旅游业发展的瓶颈。因此，在策略层面对旅游公共交通巴士设计合理的定价，既能满足大众游客的需求，又能让企业保持一定的盈利能力，对增强城市的旅游业发展动力具有实际意义。

目前国内外关于公共交通定价的研究有很多。传统的定价方法包括边际成本定价[1]、价格上限定价[2]和拉姆塞定价[3-4]。近年来，大多数学者从模型优化的角度对交通定价进行研究。Kraus等[5]考虑用户出行时间，建立城市轨道交通定价优化模型。仝允桓[6]基于乘客时间价值和交通运量的价格弹性模型，构造城市快速交通线项目的最优票价模型。周晶等[7]对公交网络系统的经营博弈问题进行研究分析，建立了经营者之间广义Nash均衡博弈模型。Thakuriah等[8]运用次优价格理论建立模型，研究运营成本与服务水平之间的最佳定价。王灿灿等[9]针对高速铁路，基于价格歧视理论提出动态定价策略。Zhang等[10]利用动态定价策略及库存定理研究旅游轨道交通定价问题。但以上研究在刻画乘客的出行选择行为时都没有考虑用户异质的情况。由于人们的社会经济特征各不相同，每个出行者具有不同的时间价值，即用户的异质性，这是出行者在时间和费用之间做出权衡的重要因素，极大地影响出行方式选择行为。因此，本文从用户异质性的角度研究旅游交通定价问题。

目前文献也有一些关于用户异质性的出行和定价问题研究。王昕等[11]针对存在异质性用户的交通路网，研究了在固定需求下用户的时间价值呈离散分布，出行费用与出行时间呈非线性关系时系统最优和多用户均衡路径选择模型。胡盼等[12]在描述广义出行成本时，引入敏感性系数来调整各服务属性在出行成本中的贡献率，研究基于广义出行成本的最优出行方案。永贵等[13]在边际成本票价和平均成本票价这2种定价组合下，将2组出行者的时间成本系数取不同值，给出异质性出行者的交通方式划分。Clark等[14]研究在弹性需求下，用户的时间价值呈离散分布时系统最优及多用户均衡解。Van Den Berg等[15]在道路系统最优收费情况下，分析异质性用户的出行选择问题。但以上研究在描述乘客出行方式的选择行为时，没有考虑到不同结构群体在选择行为上的差异，在刻画用户异质性时直接假设单位时间价值与流量呈离散分布或均匀分布或直接取值，没有反映出不同结构群体的出行特征及在选择行为上的差别。

以往对交通定价的研究较少以旅游为背景。通勤交通是有规律的交通，而旅游交通自由度很大，受旅游者主观意愿影响较大，不同结构群体在选择行为上有较大差异。张梅梅等[16]研究北京市游客对旅游交通方式的选择行为，结果表明游客的年龄对交通方式选择的影响显著。马丽君等[17]考虑不同年龄阶段游客的消费特点有着较大的差异，研究年龄结构对城镇旅游发展的影响。Schmocker等[18]研究发现居住在高密度区域的、市中心区域的老龄人口偏好于选择公共交通出行和步行。综上所述，不同年龄的游客在选择行为上有差别，且年龄是旅游市场细分理论的一个重要社会−人口学变量[19-20]。不同年龄的游客对时间价值成本有不同的感知情况，比如年轻型和老年型有较多的可自由支配时间，对时间价值相对不敏感，而中年人有自己的事业，对时间价值要求相对较高，进而影响旅游者的出行偏好、出行方式选择，从而影响到整个城市公共交通的运营管理。因此，本文考虑不同年龄游客的出行偏好，进一步探究旅游公共交通的定价问题。根据单位时间价值与年龄的关系，对游客按年龄大小编号排序，得出单位时间价值与流量的关系，将模型扩展为多人群的竞争旅游交通系统。与传统的基于广义成本的公共交通定价问题不同，基于不同年龄结构的出行偏好给所研究问题注入新的元素。

1 问题描述及交通方式流量划分结果

1.1 问题描述

游客在出行过程中会对多种交通方式进行选择，如巴士、公交、地铁、自驾。通常情况下，选择自驾或打车可以节省出行时间成本，选择公共交通方式可以节约经济成本。由于公交和地铁有政府补贴，价格过于便宜，所以本文对旅游巴士的定价不考虑公交和地铁，只考虑一个交通枢纽O至景区D的具有2种交通方式的竞争系统。交通方式A和B分别代表小汽车和旅游巴士。出行游客选择何种方式出行通常取决于广义出行成本的大小。广义出行成本考虑快速性、经济性、车内拥挤程度、衔接性等因素。由于巴士和小汽车2种交通方式都是一人对应一个座位且都不需要中转，所以每位出行者的广义出行费用由出行时间成本和出行货币成本构成。通常采用年龄分组来刻画旅游市场的行为差异。人口年龄结构通常被划分为年轻型、成年型和年老型3种类型。其对应的划分标准分别为20岁以下、21~30岁和31岁以上。而将这种类型划分标准引入旅游市场时，需要做出相应的调整。参照文献[21]，本文的分组标准分别为年轻型(18~35岁)、成年型(35~45岁)、年老型(45~70岁)。假设游客的单位时间价值在不同年龄阶段下表现为不同的线性关系，如图1所示。i=1,2,3分别表示3种游客，其中，αimin和αimax分别表示第i种游客最小单位时间价值和最大单位时间价值。

1.2 3种游客的出行成本

假设OD对第i类游客的需求量为qi，令fAi和fBi分别为第i类游客选择小汽车和巴士出行的人数，fAi+fBi=qi。针对3类游客按年龄大小从0至qi进行编号，如年轻型游客，从18~35岁按年龄大小从0~q1排序编号，由图1可以得出3类游客的单位出行时间价值随流量f的函数图像，如图2所示。βi(f)为第i类游客中第f个出行者的单位时间价值，当i=1和2时，βi(f)=α3max。小汽车和旅游巴士的出行时间分别设为tA和tB，且满足tB＞tA，pA和pB分别为小汽车/旅游巴士的经济成本，第i类游客第f个出行者选择小汽车和巴士的出行成本分别为

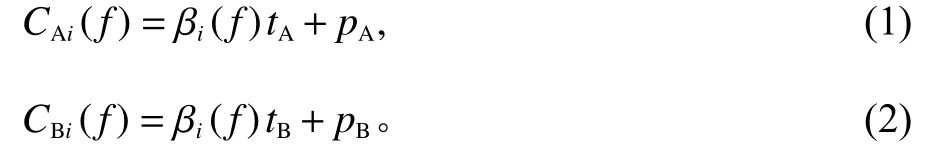
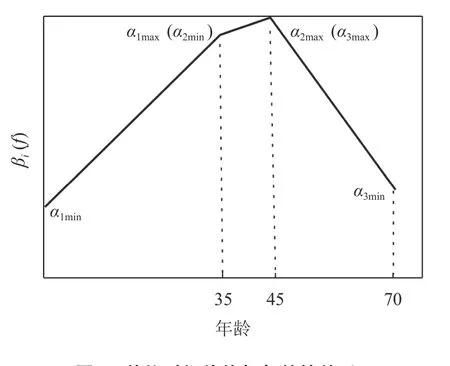
图 1 单位时间价值与年龄的关系Figure 1 Relationship between unit time value and age

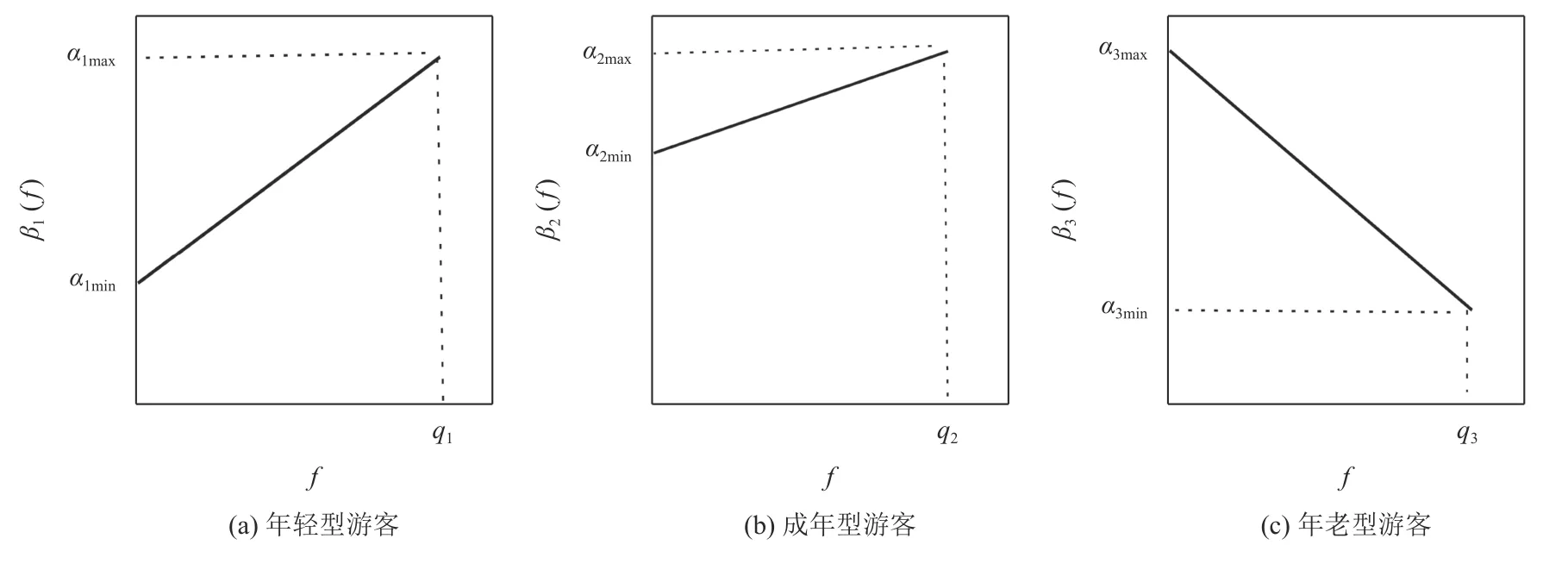
图 2 单位时间价值与流量的关系Figure 2 Relationship between unit time value and flow rate

1.3 3种游客在均衡成本下的方式划分结果

假设所有游客都是完全理性的，在2种方式竞争交通系统中选择出行成本较小的交通方式出行，则某个出行用户fie不能通过改变出行方式来降低其出行成本。fie为均衡流量即均衡的出行成本，可以表示为

可以求出，当i=1和2时，

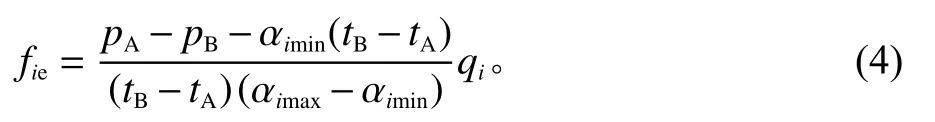
当i=3时，

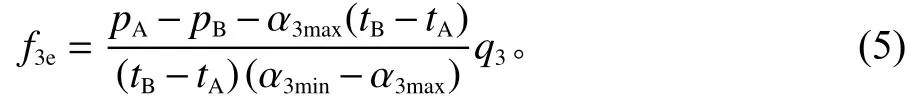
当i=1和2时，由于单位时间价值随f单调递增，年龄越大的游客时间价值成本越高，当达到均衡状态后，剩下的游客会选择小汽车以节省时间成本，即编号0至fie的游客都会选择巴士，而编号fie至

qi的游客会选择小汽车；当i=3时，单位时间价值随流量单调递减，年龄越大的游客时间价值成本越低，当达到均衡状态后，剩下的游客会选择巴士，即编号0至f3e的游客都会选择小汽车，而编号f3e至q3的游客会选择巴士。因为fie满足0≤fie≤qi，pB需满足pA−αimax(tB−tA)≤pB≤pA−αimin(tB−tA)。可得方式的划分结果如下。

1) 当pB≤pA−αimax(tB−tA)时，巴士的广义出行成本始终都比小汽车小，所以，fBi=qi，fAi=0。

2) 当pA−αimax(tB−tA)＜pB＜pB−αimin(tB−tA)时，

3) 当pB≥pA−αimin(tB−tA)时，小汽车的广义出行成本始终比巴士小，所以，fBi=0，fAi=qi。

2 巴士公司的收益函数模型及其性质

2.1 收益函数模型

旅游巴士是运营初期投资成本较大的公共交通，所以在制定票价时，需保证公司收入最大，经过一定时间才能使公司收回成本。旅游巴士的收入主要来自于票价，所以巴士公司的收益函数R=(fB1+fB2+fB3)pB。假设(tB−tA)，得出巴士公司不同阶段的收益函数为

(7)监理工作的方法及措施。指在监理过程中所采用的控制手段、制度，如指令性文件、检验手段和控制方法、工序的控制、监理订立的制度等。

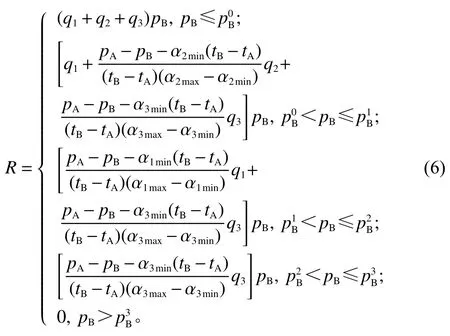
同理可得，当α1min≤α3min时，第3阶段pB的范围为收益函数在该阶段不变；第4阶段收益函数在该阶段为其他阶段的收益函数不变。当α1min=α3min时，第4阶段的函数值变为0，其他阶段收益函数不变。

2.2 模型的性质

性质1在总游客量一致，3种游客的比例不同情况下，q2越小，即成年型游客所占的比例越小，当价格大于时，巴士公司的收益会增大。这说明，当价格大于时，在统一价格下，成年型游客的比例会影响巴士公司的收益。这是因为，当q2比例减小时，时间成本之和也会减小，所以在同一价格下，选择坐巴士的乘客会增加，收益也会增加。

证明因为q2越小，q1或q3就越大。在函数第1阶段，即当pB≤时，3种游客的比例对收益无影响；但在第2阶段，因为q1和q3前面的系数比q2大，所以当q2越小，q1或q3越大时，收益会增加；当pB≥时，收益也会随着q2减小而增加。所以当定价pB＞时，收益会随着成年型游客所占的比例减小而增大。证毕。

性质2假设α1max1＜α1max2,收益函数分别为R1和R2,在同一价格下,R1(pB)≥R2(pB)。这说明在统一价格下，α1max的取值会影响巴士公司的收益，当价格大于时 ，α1max越大，巴士公司的收益越小。

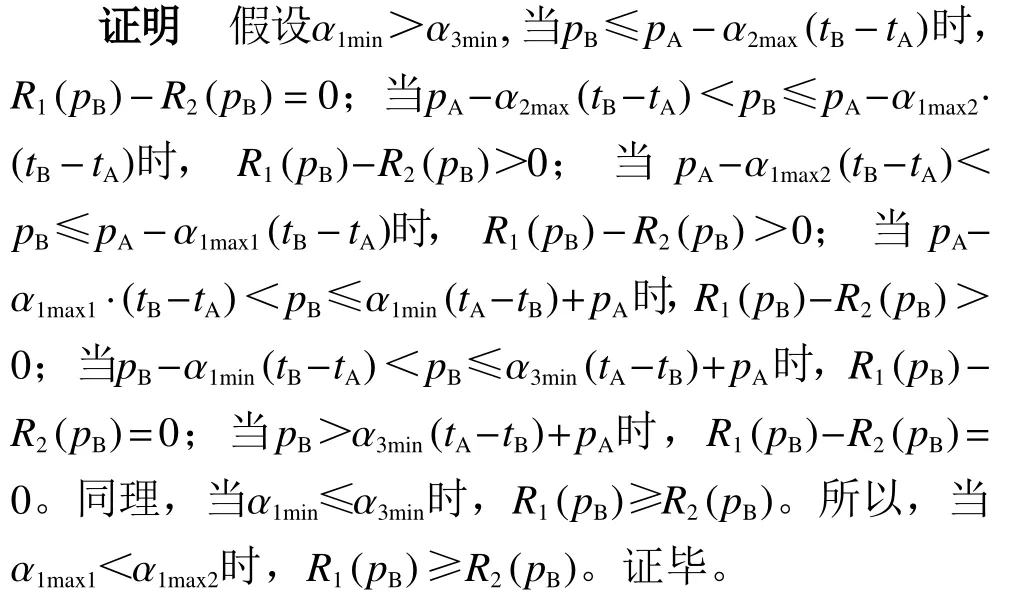
用同样的方法分析剩下的αimin及αimax对收益和定价的影响，也会得到同样的结果。当αimin及αimax中的任何一个参数增大时，部分乘客的时间价值增大，在同一价格下，选择坐巴士的游客减少,收益呈减小趋势。

3 算例分析

为了验证本文方法在实际应用的可行性及有效性，本文利用算例来计算最优票价、最优收益及各交通方式的流量分配，与此同时，对上面2个性质进行检验。基本参数取值为tA=0.7 h，tB=1h，pA=50元。OD对3种游客总的出行人数为600。因为成年型游客范围为35~45岁，只有10岁年龄差距，所占比例不超过总需求的1/3。

3.1 不同年龄阶段游客需求量对收益及票价的影响分析

图3是年龄结构比例取值不同下的收益函数图。从图3可以看出，4组策略都是在第2阶段取得最大收益。当成年型游客比例增大时，巴士公司的最优收益呈现下降趋势。同时，在同一票价下，巴士公司的收益也随着成年型游客的增多呈现下降趋势。这是因为成年型游客时间价值成本高，成年型游客中选择巴士的比例会较少，当成年型游客比例增大时，会使总人数中选择乘坐巴士的游客减少。由于年轻型游客时间价值成本较小，这阶段的票价较低，巴士出行成本始终比汽车出行成本低，所有年轻型游客都会选择巴士出行，所以fB1=q1。同时，计算出最优票价、最优收益及各交通方式的流量分配，如表1所示。

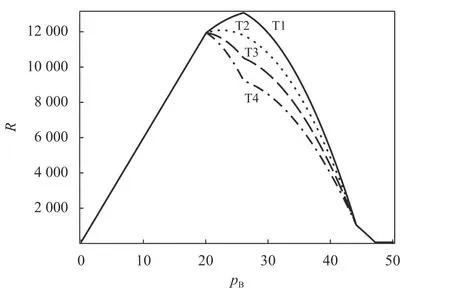
图 3 不同比例下的收益函数图Figure 3 Revenue function under different proportions

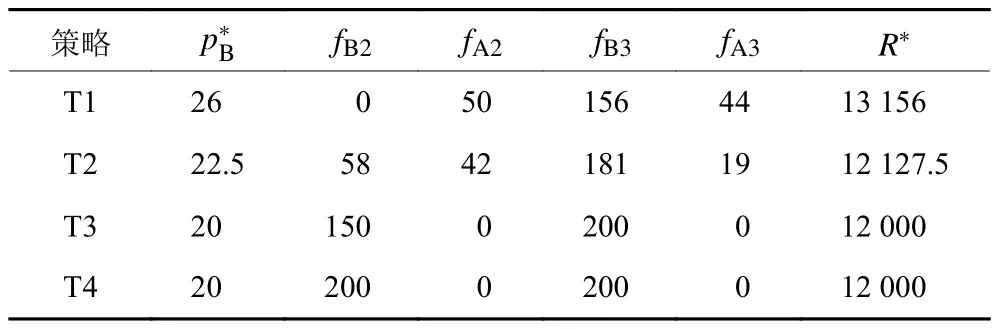
表 1 4种比例下的最优票价、流量分配及最大收益值Table 1 Optimal fare, flow distribution and maximum revenue value under four proportions

从表1可以看出，随着成年型游客的比例增大，最优定价和最优收益均呈现下降趋势。这是因为成年型游客的时间成本高，当成年型游客需求量增多时，总的时间成本就会增加，这时最优票价会降低，如果不降低票价，选择坐巴士的乘客会更少，使收益下降；当成年型游客比例增加到一定值时，最优票价为保持不变。

3.2 单位时间价值系数αimax和αimin对 收益及票价的影响分析

对性质2进行讨论。先分析参数α1max对定价和收益的影响。参数α1max是跟年轻型和成年型游客相关的参数。其他参数设置为α1min=20 元/h, α2max=100 元/h,α3min=10 元/h，3类游客数量分别为300，100，200。4组α1max的取值分别为60、70、80、90 元/h。

这时，4组不同取值下的收益函数如图4(a)所示，4组均在第2阶段取得最大收益，且当α1max增加时，收益呈现下降趋势，最优收益也呈下降趋势。α1max的增加说明部分年轻型游客和成年型游客的时间价值增加，选择坐小汽车的人数会增加；最优定价也受到影响，如果选择坐巴士的人增多，就只能通过降低票价来吸引客流。通过计算得到的最优票价 、流量分布、最优收益的情况如表2所示。

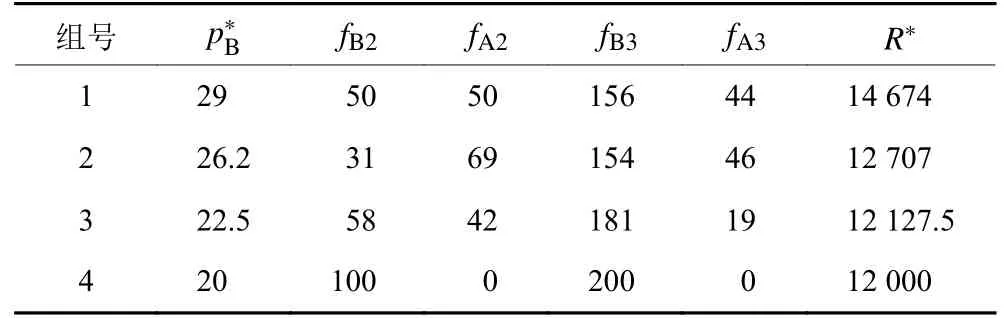
表 2 4组取值下的最优票价、流量分配及最大收益值Table 2 Optimal fare, flow allocation and maximum revenue under the four values

从表2可以看出，随着α1max增大，最优定价和最优收益均呈现下降趋势。这是因为，当α1max增大时，年轻型和年老型游客的时间价值增大，总时间成本增加，这时最优票价会降低。用同样的方法分析α1min、α2max、α3min，得到的收益函数随经济成本变化图分别为图4(b)、4(c)及4(d), 且结论与α1max相似。

4 结论

本文研究了不同年龄阶段游客的出行成本及出行方式选择问题，出行方式受票价和出行时间影响，出行时间成本随年龄变化而变化，讨论3种游客不同比例及单位时间价值系数的变化对定价和收益的影响，得出以下结论。当成年型游客比例增加时，最优定价及最优收益呈下降的趋势，成年型游客对时间敏感，需降低票价或出行时间来减小出行成本；当4个参数 (α1max、α1min、α2max和α3min) 增加时，部分游客的单位时间价值变高，游客的时间价值成本之和增加，在同一价格下，选择坐巴士的游客减少，巴士公司的收益也随之减小。因此，可根据客流年龄结构比例情况，适当调整票价。随着社会的发展，人们的单位时间价值会出现增加的趋势，一味降低票价来提高竞争力将会导致企业失去盈利能力，这时需降低游客的出行时间，为游客创造良好的旅游体验。本文在定义出行时间成本时，假设不同年龄阶段游客的单位时间价值随年龄呈不同的线性关系，在实际情况中，可能呈非线性关系，可考虑将其作为下一步的研究方向。

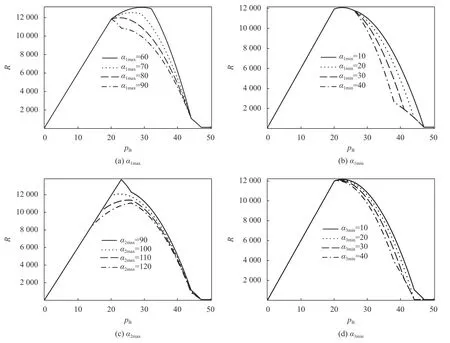
图 4 4个参数取值不同时的收益函数Figure 4 Revenue function with different values of four parameters