考虑随机市场需求和不同博弈地位的双渠道供应链策略分析

李宗活，杨文胜，刘晓红

(南京理工大学 经济管理学院，江苏 南京 210094)

随着互联网技术的发展，快速、便捷、多选的网络购物模式越来越受消费者欢迎，企业纷纷引进网络销售渠道满足消费者偏好，网络渠道与传统实体渠道并存的双渠道销售模式已成为企业营销的一大特点，如IBM、思科、雅诗兰黛等。随着渠道选择多样性的增加，加之产品更新换代的加快、产品个性化需求的提升，市场需求的复杂性与不确定性骤然增加，这对双渠道供应链产品定价、库存控制及供应链利益协调产生重要影响[1]。而在供应链上下游企业价格、库存及利益协调相关决策中，不同博弈地位的策略选择不同，决策的先后顺序显著影响着整个供应链系统收益，如零售商作为主导方的沃尔玛与小型制造企业决策、制造商作为主导方的苹果与小型零售商决策、制造商与零售商势力相当的宝洁与沃尔玛决策等。对此，如何基于自身博弈地位作出市场响应、如何应对不确定市场需求进而展开价格与库存管理是供应链企业迫切需要解决的问题。

以往关于随机需求的供应链研究多从传统实体渠道展开。如Güray[2]在单一供应商和零售商组成的两级供应链系统中考虑了随机需求问题，通过不同契约的设计实现供应链协调。Wang[3]针对具有需求变动的服装行业，通过一个单位数量折扣契约实现传统渠道服装供应链的有效协调。Liu等[4]考虑两级供应链中的需求不确定性因素，通过回购契约协调存在顾客退货的制造商和零售商利益关系。将随机需求引入到双渠道供应链的研究较为少见，如Wei[5]分析随机需求下的双渠道供应链渠道冲突问题，并通过一个改进的回购契约进行协调。Huang[6]分析存在不确定市场需求扰动的双渠道供应链定价问题，认为通过价格的及时调整可提高供应链绩效。

有关双渠道决策问题的研究侧重于对比分析分散与集中决策的策略差异，进而设计合作契约协调供应链，如王先甲等[7]、Kong等[8]、王垒等[9]。这些研究多视制造商为主导者，实际上，随着以消费者为中心的营销模式的兴起，零售商比上游企业掌握着更多更真实的市场信息[10]，它们正逐步从制造商手中夺取主导权，如沃尔玛、家乐福、麦德龙等零售巨头。有学者开展以零售商为渠道主导者的研究[11-12]，但鲜有对比分析不同主导者情形下的策略差异，且结合随机市场需求进行分析的研究尚不多见[13-14]。

于此，本文将随机市场需求考虑到双渠道供应链中，通过决策者的博弈地位刻画主导属性，分别构建制造商主导、零售商主导和同等博弈地位的双渠道供应链博弈模型，探讨不同博弈地位和随机市场需求共同作用下的供应链企业响应策略，为双渠道供应链管理提供理论参考。

1 问题描述及模型假设

考虑由单一制造商和零售商组成的双渠道供应链系统。制造商一方面以批发价格pw将产品销售给零售商，另一方面以价格pe在网络渠道销售产品。零售商根据市场需求确定pw的加价率，进而在实体渠道以零售价格pr销售产品。实体渠道和网络渠道市场需求具有随机性，这里，采用线性加性不确定性刻画随机市场需求[4]，即实体渠道和网络渠道市场需求分别为

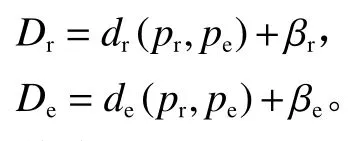
其中，dr(pr,pe)和de(pr,pe)为基本市场需求，设定其表达式为

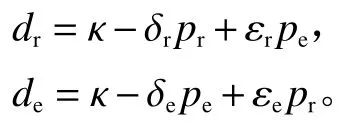
式中，κ为最大市场容量，δi(i=r,e)为渠道内价格弹性系数，εi(i=r,e)为渠道间价格弹性系数，刻画渠道间的替代效应。为计算方便，将价格弹性设定为δ=δr=δe、ε=εr=εe，即

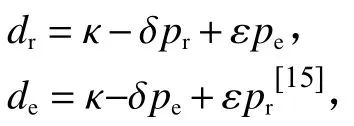
且存在δ＞ε，表明渠道本身的价格弹性大于渠道间的价格弹性。βr和βe是独立于基本市场需求的随机变量，其概率密度和概率分布分别为f(βr)、F(βr)和g(βe)、G(βe)，且f(βr)和F(βr)在βr∈(0,a]上连续可微；g(βe)和G(βe)在βe∈(0,b]上连续可微。

为应对随机市场，零售商与制造商制定的库存水平分别为Qr、Qm。制造商单位产品缺货成本为cms、库存成本为cmI；零售商单位产品缺货成本为crs、库存成本为crI。不考虑制造商生产成本，该设定不影响结果的讨论。

考虑制造商主导(ML模式)、零售商主导(RL模式)及同等博弈地位(ES模式)3种决策模式。3种决策模式的双渠道供应链系统如图1所示。

2 模型构建及分析

在双渠道供应链系统中，制造商利润函数为

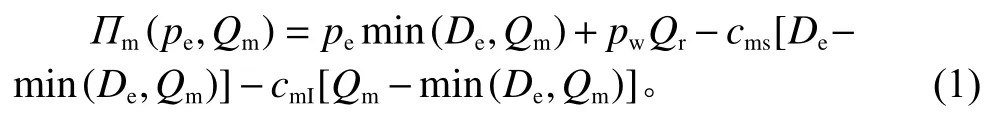
式(1)中，第1项为网络渠道收入；第2项为实体渠道收入；第3、第4项分别为缺货成本和库存成本。当De＞Qm时，供不应求，存在缺货成本；当De＜Qm时，供过于求，存在库存成本。

零售商利润函数为

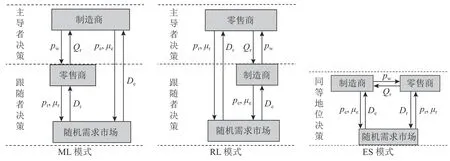
图 1 3种决策模式的双渠道供应链系统Figure 1 Dual-channel supply chain system of three models

式(2)中，第1项为零售收入；第2项为订货支出；第3、第4项分别为缺货成本和库存成本。同理，当Dr＞Qr时，供不应求，存在缺货成本；当Dr＜Qr时，供过于求，存在库存成本。为方便表达，令µr=Qr−dr(pr,pe)，µe=Qm−de(pe,pr)，则Qr和Qm决策分别通过µr和µe表征，表示为满足随机需求部分制定的库存水平，则可将式(1)、式(2)转化为

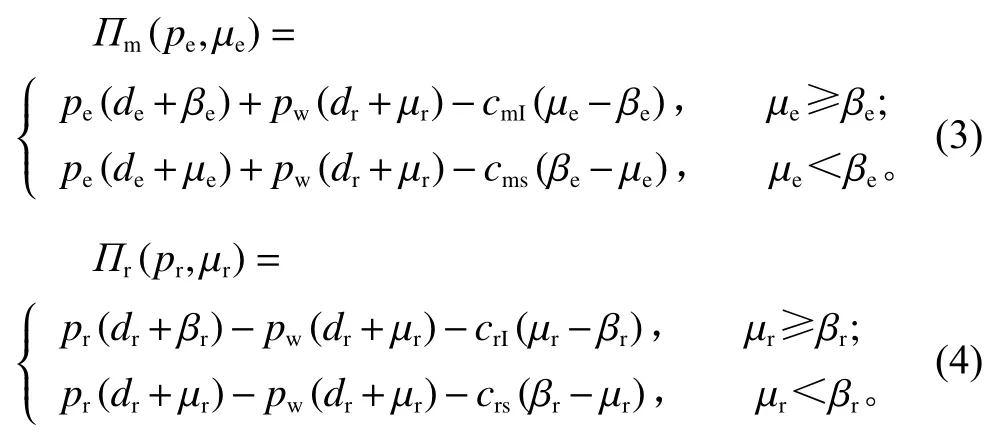
2.1 制造商主导下的Stackelberg博弈(ML模型)

制造商主导的市场结构代表由大型制造商和相对较小的零售商组成的市场，在该双渠道供应链模式中，制造商先行动，对pe、µe进行决策，零售商获得制造商的决策信息后，作出pr、µr的响应。根据式(3)、式(4)，供应链决策问题为

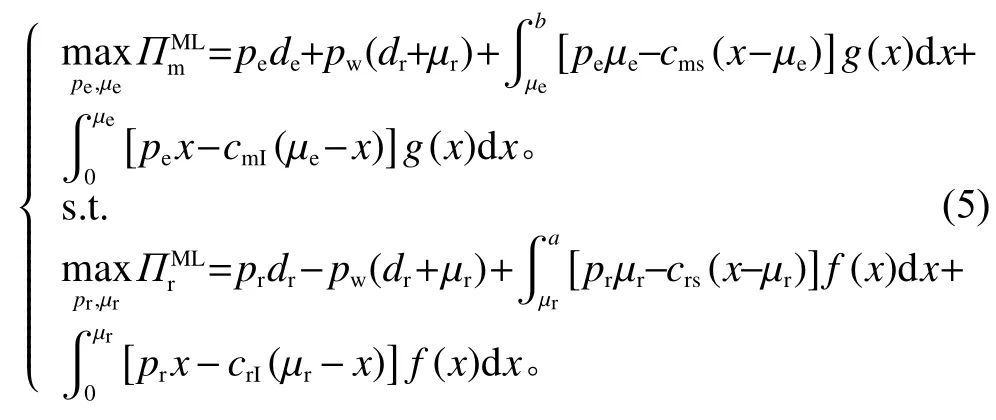
求解制造商决策问题，获得命题1。

根据上述分析及逆向求解法，可得制造商决策问题为

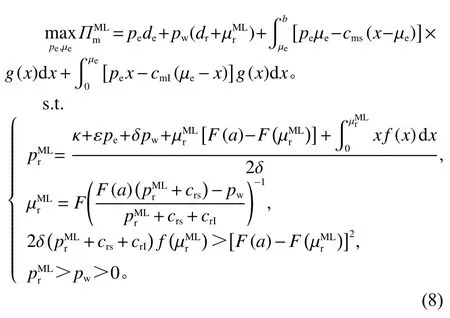
由于制造商决策问题包含隐函数且为非线性规划问题，难以求得其显性解，下文通过数值算例揭示其管理学意义。

2.2 零售商主导下的Stackelberg博弈(RL模型)

零售商主导的市场代表由零售巨头以及小型制造商组成的市场，在该双渠道供应链系统中，零售商先行动，对pr、µr进行决策，制造商获得零售商的决策信息后，作出pe、µe的最优响应。根据式(3)、式(4)，供应链决策问题为

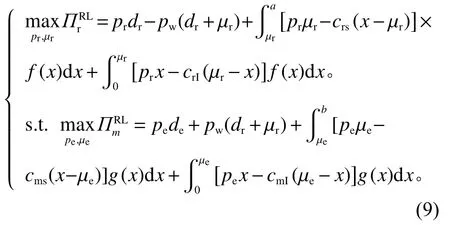
求解制造商决策问题，获得命题2。

将式(10)、式(11)代入式(9)，可得制造商最优利润。命题得证。

根据上述分析及逆向求解法，可得零售商决策问题为

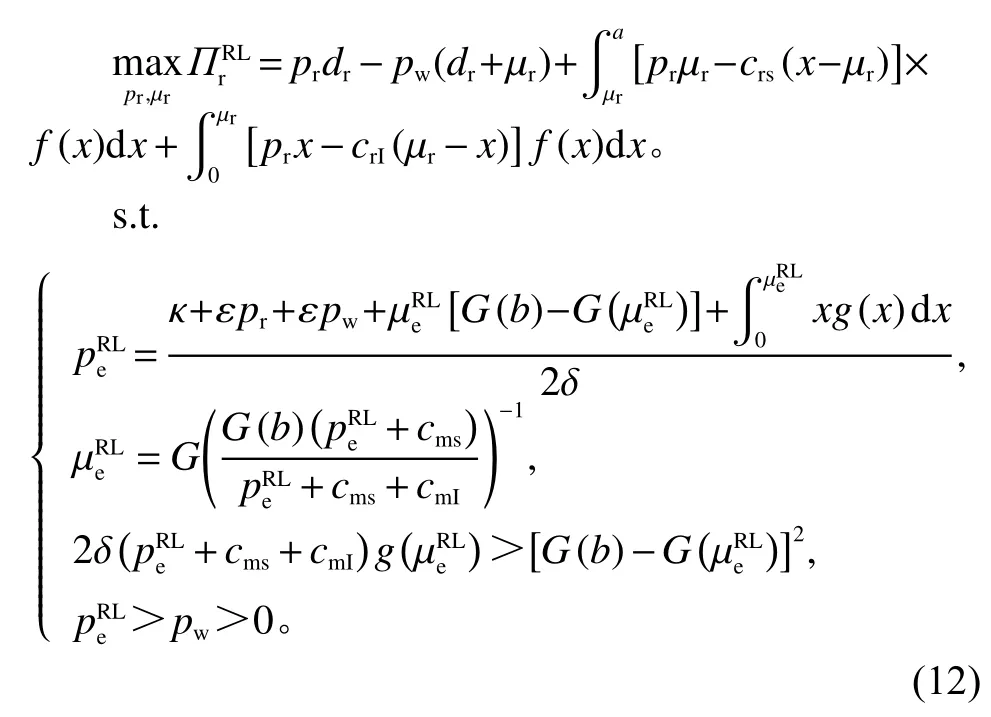
2.3 同等决策地位Nash博弈(ES模型)

同等决策地位情形代表一类由相对小到中型的制造商和零售商组成的市场，通过Nash博弈分析同等决策地位下的双渠道均衡，并与非对等地位情形进行对比。根据式(3)、式(4)，同等决策地位下的供应链决策问题为

根据Nash博弈求解以上决策问题，获得命题3。

命题3存在组合决策实现成员企业利润最优化。

证明该决策问题为静态博弈，故通过Nash博弈分别求解制造商和零售商的决策问题。解的唯一性证明同以上，在此不作赘述。由一阶条件可求得零售商和制造商最优定价与库存。联立一阶最优反应，获得四元方程组

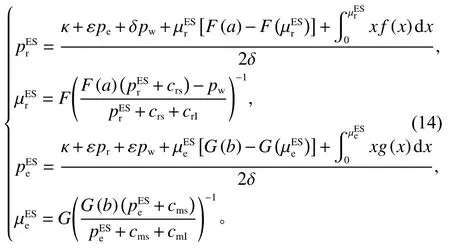
求解四元方程组可得同等博弈地位下的双渠道最优决策组合，再代回式(13)计算制造商和零售商最优利润，实现Nash博弈均衡。命题得证。

同理，最优解的数学表达式较为复杂且包含隐函数，通过数值算例揭示其管理学启示。

3 数值算例

本文侧重于分析不同博弈地位和随机市场需求对供应链决策的影响。为避免不必要的复杂技术对分析结果的影响，在满足命题1~命题3的参数约束条件下，设定非决策变量数值为crs=cms=2，crI=cmI=3，δ=1，βr∈U(0,5)，βe∈U(0,5)，其他参数设置为ε=0.6，κ=10，pw=6。采用Mathematica和Matlab计算各决策变量和利润的显性解，比较不同决策模式下的策略差异，并绘制随机需求对定价、库存及利润的影响趋势图，揭示管理启示。

1) 双渠道供应链系统的均衡分析。

3种决策模式的最优定价、随机库存及利润如表1所示。

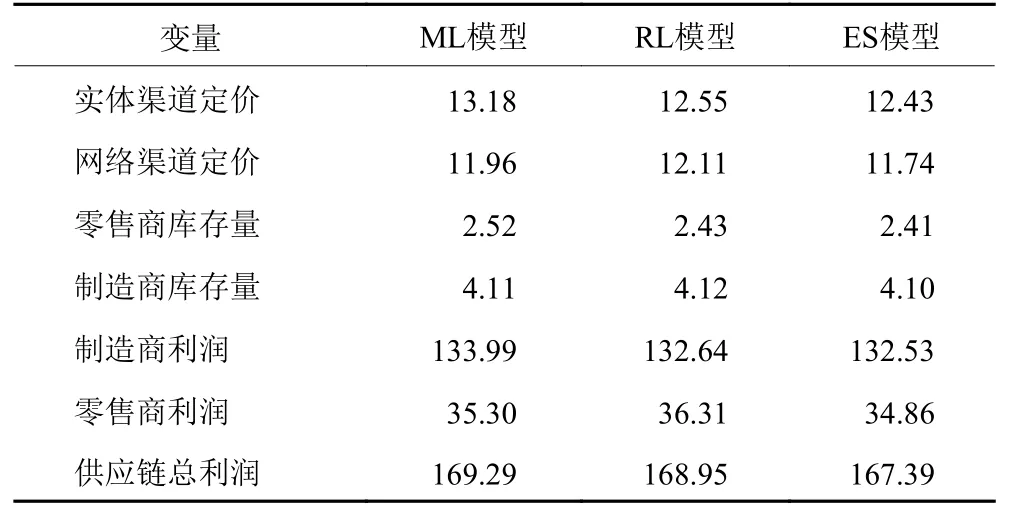
表 1 制造商与零售商最优决策Table 1 The optimal decision-making of manufacturer and retailer

由表1看到，从渠道定价角度，3种决策模式的实体渠道定价均大于网络渠道定价RL,ES)，与当前主流研究一致；不同决策模式之间，制造商主导的实体渠道定价最高，零售商主导的网络渠道定价最高，即进一步分析发现，主导权从制造商转移到零售商过程中，实体渠道定价降低，网络渠道定价升高，说明主导方可凭借市场垄断力量获得低价优势。同等决策地位情形下的实体渠道和网络渠道定价均最低，原因在于博弈双方交互竞价以争夺市场份额，价格降低，这与Gao[16]的研究结论一致。

从库存角度，3种决策模式的网络渠道库存量均大于实体渠道库存量在价格与需求的反函数作用下，越低的渠道价格获得越高的需求量，故用于满足市场需求的库存量也越高；不同决策模式之间，制造商主导的实体渠道库存量最大，零售商主导的网络渠道库存量最大，即原因在于主导方拥有更强的价格控制权及更多的市场信息，其市场应对能力较强，可有效配置库存，而作为追随者，需增加自身的库存量以应对市场需求的不确定性。同等博弈地位情形下的实体渠道和网络渠道库存量均最小，该情形下双方具有共同的市场信息，博弈双方基于自身利益不断更新库存策略，可将库存风险降到最低，因而其库存量最低。

从供应链利润角度，无论制造商主导亦或零售商主导，主导方利润均最大，说明供应链成员可以凭借主导权为自己谋取更大收益；同等决策地位情形的利润最小，一者由于博弈双方产品定价较低，市场需求及库存量均较小，利润较小，二者在于双重边际效应降低了个体收益；制造商主导型供应链的整体利润水平高于零售商主导型原因在于制造商控制网络渠道和实体渠道，具有更强的渠道整合能力。相反，当零售商拥有主导权时，往往激励制造商提高供应量。这种激励机制在一定程度上导致产能过剩，出现供过于求的局面[17]，整体供应链利润越低。

2) 随机需求对渠道定价、库存及利润的扰动作用。

通过不同的均匀分布范围表征随机需求的波动性，由此分析随机需求对定价、库存及利润的扰动作用，即考察实体渠道和网络渠道随机需求(βr和βe)分别服从U(0,5)、U(0,6)、U(0,7)、U(0,8)、U(0,9)、U(0,10)均匀分布时渠道定价、库存及利润的变动趋势，结果如图2所示。

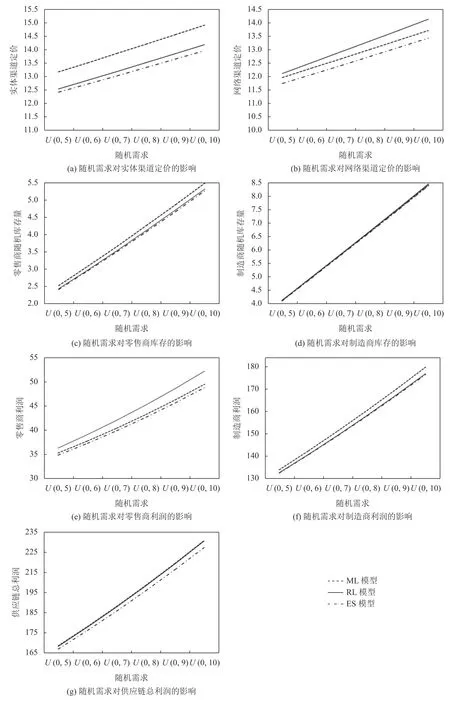
图 2 随机需求对定价、库存及利润的扰动作用Figure 2 The impact of stochastic demand on pricing, inventory and profit

由图2看到，市场需求波动越大，3种决策模式下的渠道定价、库存及供应链利润均呈上升趋势。较大的市场需求波动迫使供应链企业增加库存量，此时，利润最大化目标驱使下，制造商及零售商均通过抬高渠道价格弥补库存成本支出，在订货量及价格均提高的情况下，供应链企业的边际收益增加，利润提高。实际上，尽管供应链企业利润得到提高，这在一定程度上引发产能过剩的困境，进而导致社会福利下降。

另外注意到，市场波动越大，制造商主导情形的实体渠道价格增幅最大，零售商主导情形的网络渠道价格增幅最大，即这说明面对随机需求市场，主导方对自身渠道价格具有更强的把控能力，同等博弈地位情形下双方具有更敏锐的风险规避性，该情形的价格调整幅度最低。同理，库存增幅主导方在应对需求波动上显示更强的控制能力，追随者缺乏足够的市场信息，需增大库存以应对需求波动。利润变动幅度的大小关系为这说明由主导权获得的价格把控能力及库存应对能力使主导者获得更大的利润增幅，而同等决策地位的制造商和零售商利润则因双重边际效应被削减，利润增幅较小，可见制造商和零售商应避免同时单独做决策。

4 结论及管理启示

复杂的市场环境下，供应链末端需求面临诸多不确定性，而博弈地位的不同对供应链策略产生重要影响。本文综合考虑随机需求和不同博弈地位两方面影响因素，分别构建制造商主导、零售商主导及同等博弈地位的双渠道供应链博弈模型，探讨随机需求对渠道定价、库存及利润的影响，分析不同博弈地位的策略差异。管理学启示揭示如下。

1) 拥有渠道主导权的博弈方获得价格优势，且市场应对能力越强，可以较小库存满足市场需求。这种价格把控权及库存应对能力使主导者获得较大的利润。2) 具有同等博弈地位的博弈双方可根据共同市场信息及竞争对手策略不断更新自身的策略选择，进而配置较小库存满足随机市场需求，同时，双方的竞价行为使渠道定价降低，且在双重边际效应下，双方利润水平均较小，应避免同时单独做决策。3) 制造商主导型供应链具有更强的渠道整合能力，供应链的整体利润水平高于零售商主导型。4) 市场需求波动越大，渠道定价、库存量及供应链利润均呈上升趋势，主导方的利润增幅较大。研究结论可为随机市场需求下双渠道供应链主导者和追随者决策提供理论建议。

未来的研究可针对不同主导地位的双渠道供应链系统，设计不同契约协调参与方利益，同时可将需求随机性扩展为考虑产出和需求双边随机情形。另外，决策者和消费者类型及风险偏好行为的不同可能呈现不一样的结果。这些研究将是未来有意义的探索。