基于运行特性的港湾式公交站延误时间研究

柳伍生，潘自翔，周 骞，郑天玉

(长沙理工大学交通运输工程学院，长沙410014)

0 引 言

公交站是公交网络中的一个瓶颈，停靠站的延误决定站点和附近路段的通行能力和服务水平[1].公交在站台延误时间受公交在站内外运行特性影响，从公交进站、停靠、出站的运行特性角度，可以探讨车辆在站台延误产生、变化的内在机理，研究港湾式站台车辆延误时间问题.近年来，国内外学者对公交在站台运行进行大量研究，包括车辆在站点延误时间、站台通行能力及对相邻道路交通的影响，研究方法集中在软件仿真试验、计算模型的改进、回归分析等，并进行实证分析和数值拟合分析.在研究公交在站台延误及站台通行能力方面，SUN F.等[2]将马尔科夫链嵌入到传统的稳态排队理论并提出站点车辆延误的计算模型.于乐乐等[3]建立车辆延误分阶段、分情形的数学模型，给出公交在站台的延误时间估算方法.GU等[4]以公交与小汽车为研究对象，指出将公交站设在其相邻信控交叉口下游，可以缩小车辆延误时间，而小汽车则相反.刘璐等[5]从全过程时间的角度对经典的通行能力模型进行改进，并对数值算例结果进行曲线拟合.刘伟玲[6]结合通行能力定义分别建立直线式和港湾式站点通行能力定义，并搭建VISSIM 仿真模型，将其与理论模型对比分析.文献[1]考虑车辆停靠时间、交叉口配时及泊位数等影响因素，给出较经典的车站通行能力计算方法.

在研究停靠站或公交进出站对相邻路段交通的影响方面，主要集中于通行能力、速度等；Gu等[7]剖析位于交叉口上游处公交站对附近路段车辆的影响过程.Zhang等[8]基于速度，评价公交进出站时对机动车、非机动车等的影响.严亚丹等[9]使用无人机获取数据，研究公交车进出不同形式停靠站对主干路路段的交通影响.综合上述，既有研究未深入分析延误与车辆运行特性的关系，缺少对延误产生的内在机理剖析，因而无法评估公交在不同泊位站台处进站、停靠和出站时量化的延误时间及随多因素变化的情况.

本文从时空占用角度研究公交在站台的延误，对公交在站台的运行状态做0-1 分类，区分不同泊位港湾式站台形式对车辆延误的影响，考虑相邻车道流量、公交到达率等因素，构建延误时间模型，并进行模型验证与数值分析.

1 站台车辆运行时间描述

1.1 研究对象

研究的停靠站为城市基本路段路内单泊位港湾式公交站和多泊位港湾式公交站(简称公交站或站台)，以较典型的城市道路双向四车道，站台设置在机非隔离带的左侧为例，其模式如图1和图2所示，图2中，d为公交车长，泊位命名规则为：n≥m.

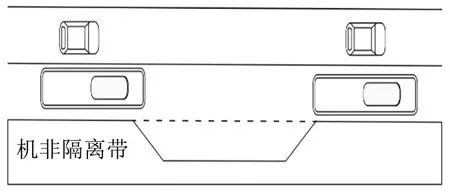
图1 单泊位港湾式公交站Fig.1 Single parking space of harbor-shaped bus stop

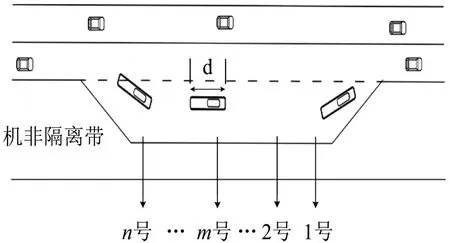
图2 多泊位港湾式公交站Fig.2 Multi-parking spaces of harbor-shaped bus stop

1.2 车辆运行过程与时间

公交在站台运行前后的过程描述如下：①到达站台后在站外等待(需等待进站车流)；②减速进站；③进入泊位后进行停靠服务；④停靠服务结束后等待前车(多泊位站台需等待车流)；⑤行驶至驶离泊位(多泊位站台)；⑥等待汇入相邻车道(需等待出站车流)；⑦加速出站.将公交在站台的延误按阶段分类，如图3所示.

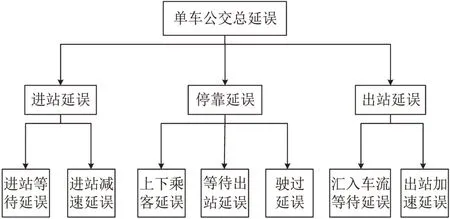
图3 公交在站台延误分类图Fig.3 Bus stop delay classification chart

2 延误的主要影响因素分析

(1)上下车乘客数.

乘客上下车延误是确定公交停靠延误的基础.任何情形下，公交停靠延误与上下车乘客数成正相关关系.研究表明[1]最繁忙车门所服务的乘客数是公交停靠延误的关键因素，在此车门的上下车乘客比例对停靠延误产生重要影响.

(2)有效泊位数.

车辆在多泊位站台内停靠时会相互干扰，故泊位是未完全利用的，引入有效泊位数来描述泊位的利用率.通过泊位数从1增加到4，对各因素进行影响分析[3]，针对多泊位站台公交停靠时互相影响的情况，把在站公交停靠的状态分为后方公交需等待前方公交完成服务再行驶和不需等待直接行驶到驶离泊位.

(3)相邻车道流量.

当公交准备出站时，将其出站状态分为直接出站和需等待再出站.对于需等待再出站的车流，其等待延误时间与相邻车道的流量密切相关,延误时间随流量的增加而增加[1].

(4)公交到达率.

公交的到达频率越高，站台的停靠压力越大.若站台所有线路的公交发车频率过高，泊位空闲的概率变小.当站内所有泊位被占用时，到达的公交需要等待站内车辆服务结束后才能驶入站台，故将公交进站状态分为直接进站和需等待进站.

3 模型构建

3.1 模型假设

(1)公交在站台内、外的运动是匀变速运动，加、减速度为a1和a2.

(2)站台的公交均为两车门，前门上车，后门下车.

(3)多泊位站台的停靠组织策略为顺序进出站，依次停靠.

3.2 进站延误时间模型

3.2.1 排队论分析

以长沙市雨花区部分港湾式公交站为例，通过人工采集结合视频的方法于2019年8月6～23日进行调查，统计得到各项参数.站点基本情况和到站频次统计如表1所示.

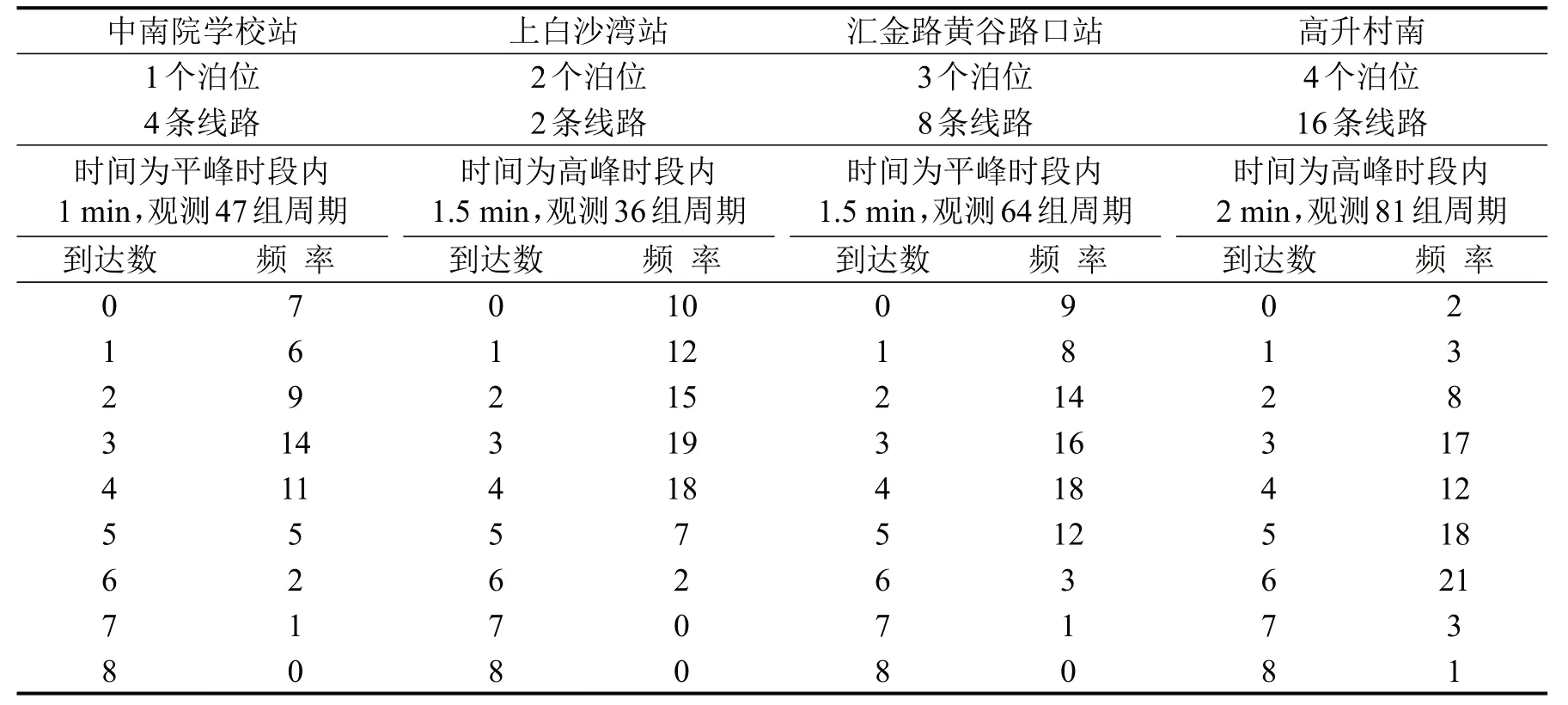
表1 公交到站统计Table1 Statistics of bus arrivals

统计公交到站频次和在站服务时间，计算到站统计样本的期望m和方差S为

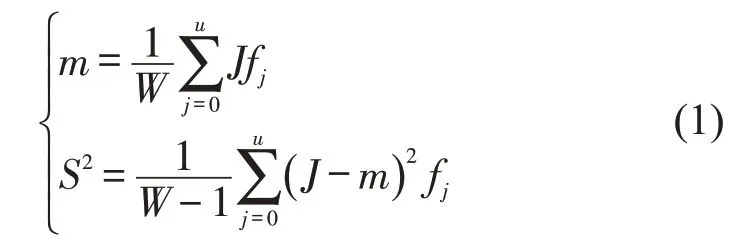
式中：W为间隔数；j为到达数；fj为j出现的频数；u为fj个数.

将表1的数据带入式(1)，得到4个站点到达数的均值和方差，分别为(2.56，2.74)、(2.42，2.57)、(2.68，2.73)、(3.03，3.22).4个站点的S2m都很接近1，表明到达分布可用泊松分布拟合，拟合结果表明泊松分布可有效描述站台的公交到达特性.

选取K-S 检验方法验证公交在站服务时间所服从的分布，用三种分布函数拟合公交在站服务时间，K-S检验结果如表2所示.结果表明：埃尔朗分布K-S值在三个分布中最小，埃尔朗分布表现远好于正态分布，略好于对数分布，拟合效果最好.

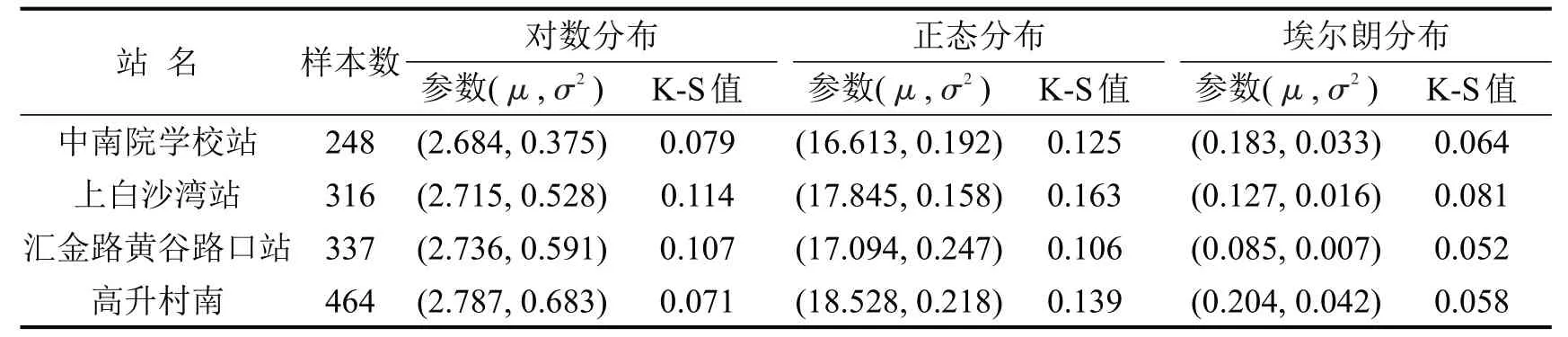
表2 公交在站服务时间的分布函数拟合Table2 Fitting of distribution function of bus service time at stations

公交到达服从泊松分布，在站服务时间服从埃尔朗分布.用M/Ek/1(N)排队模型模拟公交进站过程，将所有线路的发车频率之和代替站台的公交到达率λ，平均服务率为μ，系统的服务强度为ρ，则有

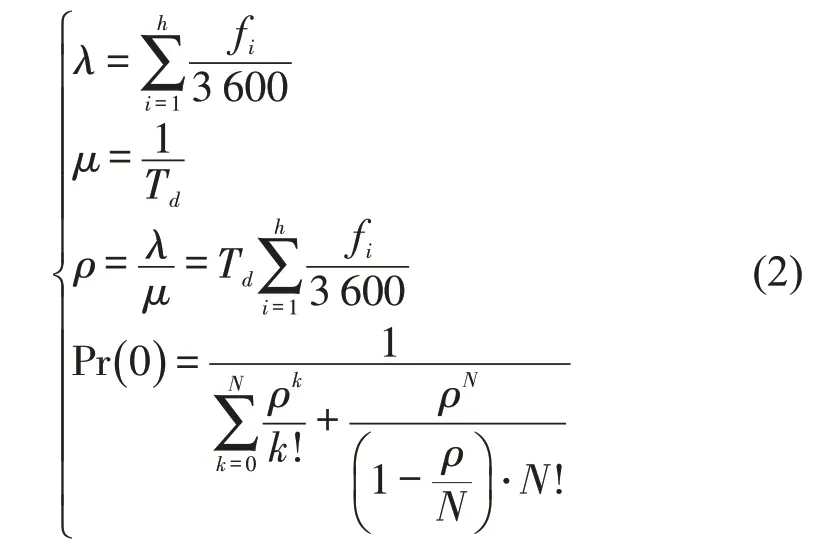
式中：fi为站台的第i条线路对应的到达频率；h为站台内线路的总数；Td指经过该站台的单车平均服务时间；k是站台内实际的车辆数；Pr(0)是站台无车辆的概率.

3.2.2 进站等待时间

当公交到达单泊位站台需要在站外等待，则其等待时间t1受站台内车辆的上下车时间及前方的公交车数量w和它们的停靠时间影响，对多泊位站台用M/Ek/N模型分析公交在站外的平均等待时间t2，为

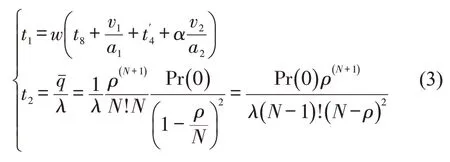
式中：t8为车辆起步时间；为每辆车的平均上下乘客时间，等于总的乘客上下车时间t4的平均值；α为修正系数，修正部分公交等待未结束就开始启动的情况，取0.5；v1、v2为车辆进站和出站时的速度；为站台排队车辆的平均排队长度.

3.2.3 进站减速时间

进站减速延误为车辆从进站速度v1减速到0的情况，延误时间t3为

3.3 停靠延误时间模型

3.3.1 上下车乘客时间

上下车乘客时间t4取决于最拥挤车门的乘客数和该车门每人平均上车或下车过道通过时间ta和tb，忽略开关门的延误时间，t4为

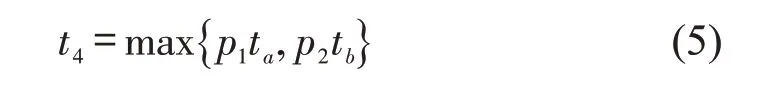
式中：p1、p2为每车最拥挤车门的上车和下车乘客数.

3.3.2 等待出站时间

当公交在站台停靠服务结束后发现前车还未驶离，这时就产生等待出站时间.公交到达站台的间隔时间服从负指数分布[6]，概率密度函数fp(t)和到达间隔时间期望Ep(t)为

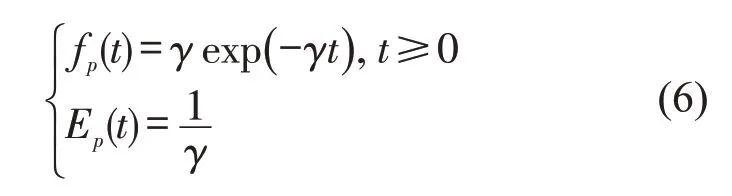
式中：γ为负指数分布参数.

公交在站服务时间为一阶埃尔朗分布[6]，埃尔朗分布函数式fu(t)和公交在站停靠时间的期望E(u)为

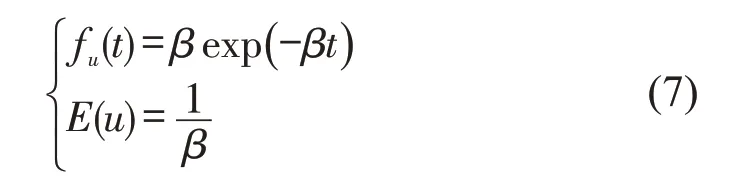
式中：β为埃尔朗分布参数.

据公交到达间隔时间分布函数和在站停靠时间的期望，得到第n号泊位公交等待第m号泊位公交服务结束所耗费时间的期望为

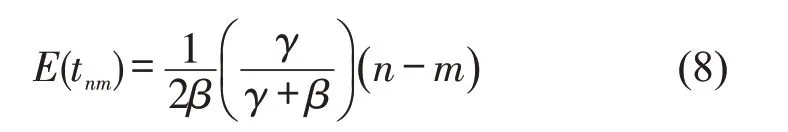
第m号泊位公交完成服务的概率Pmd为

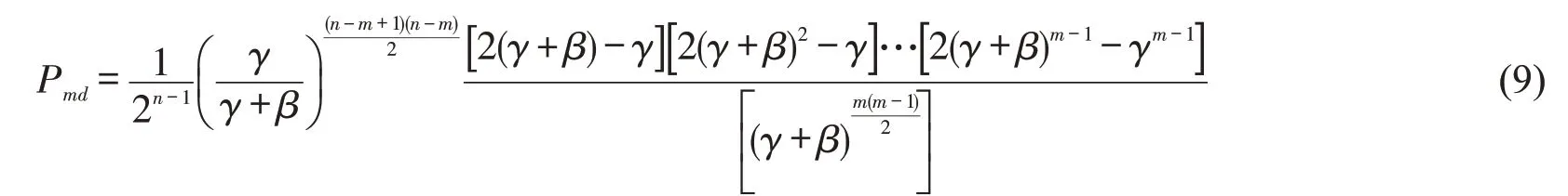
根据各泊位停靠公交完成服务的概率和期望，得出第n号泊位公交的等待时间为

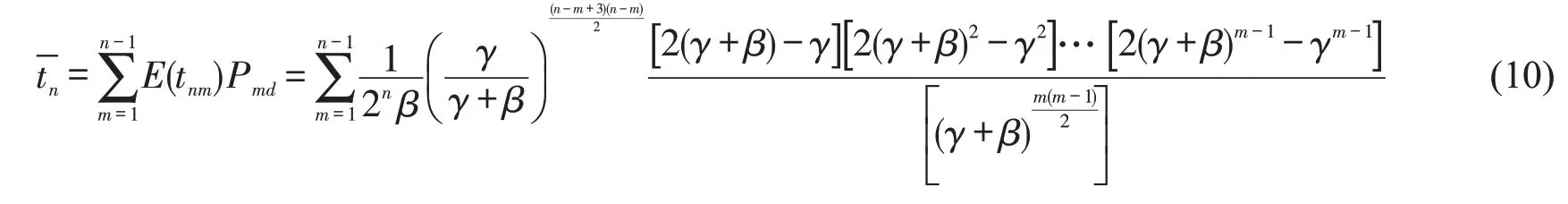
3.3.3 驶过时间

根据多泊位站台内车辆运动过程，公交在站内需行驶过自身长度和站台内泊位长度才到达驶离泊位.由运动学原理得到驶过时间t5为

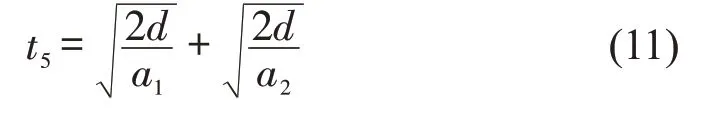
3.4 出站延误时间模型

3.4.1 汇流等待时间

公交到达驶离泊位后要汇入相邻车道车流，由于车流车头时距过小需要等待的时间，即汇流延误时间.假设K表示公交在出站过程中试图汇入车流的次数，将公交汇流的行为认为是伯努利实验[5]，服从参数是P的几何分布，公交在第K次尝试后汇入成功的概率P(K)为

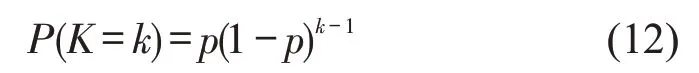
式中：p为公交每次成功汇入相邻车道的概率.

相邻车道车流的车头时距分布用负指数分布模型描述[1].设车头时距T，负指数分布参数为σ,τ为公交汇入相邻车道可接受的最小间隙时间,则

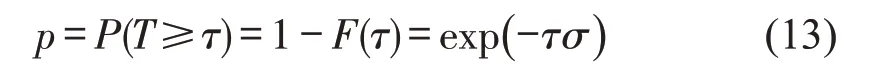
式中：P(T)为相邻车道车头时距为T的概率；F(τ)为车头时距取τ时的分布函数.

根据离散型随机变量的数学期望公式，公交试图汇入相邻车道车流的次数为

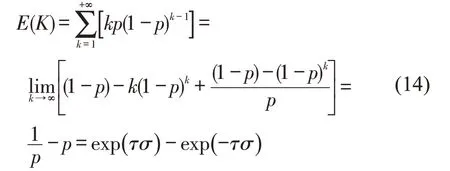
在调查得到车头时距分布后，求出汇流延误时间t6为

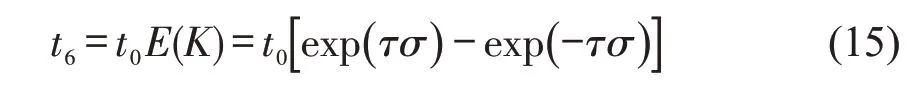
式中：t0为车辆每次尝试汇入车流的损失时间，通过实测数据进行参数标定.

3.4.2 出站加速时间

出站时公交的延误时间t7为

3.5 港湾式公交站延误时间模型

3.5.1 决策变量

x、y和z是模型决策变量，表达式为

3.5.2 单泊位公交站延误时间模型

模型从时空占用方面分析车辆在站的延误时间，由公交进站、停靠和出站延误的算术叠加值构成车辆在单泊位站台的延误数值T1，构建的模型为

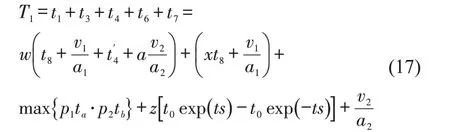
3.5.3 多泊位公交站延误时间模型

多泊位站台仅在进站延误和停靠延误与单泊位站台存在差别，仍以各阶段延误的算术叠加值构成车辆在多泊位站台的延误数值T2，模型为

4 模型验证与数值分析

4.1 数据获取

以表1的4个站点作为模型验证和数据采集对象.采集的数据为：①公交在站台的到达率，②车辆停靠时最拥挤车门的上、下客数，③公交出站时相邻车道流量，④公交在站台运行状态的0/1决策情况，⑤公交进站、出站的速度和加速度及其它在实际场景下模型的参数.并获得不同影响因素下车辆的实际延误时间.

4.2 模型验证及各因素的影响分析

计算车辆在站台延误时间并绘制变化曲线，对比模型计算值与实测的延误时间，分析各因素对车辆延误的影响.

给定上下车乘客数、相邻车道流量等参数条件下，用式(17)和式(18)计算，绘制车辆延误随到达率的变化曲线并与实测延误值比较，如图4所示.发现公交在站台延误随到达率增大呈指数增长趋势，不同泊位数下延误对到达率的敏感程度存在差异，当到达率在0.01～0.03 veh/s时，不同泊位的延误相差无几，即曲线反应相互交汇，当到达率超过一定值时，延误陡增，发现模型计算值与实测值较相符.

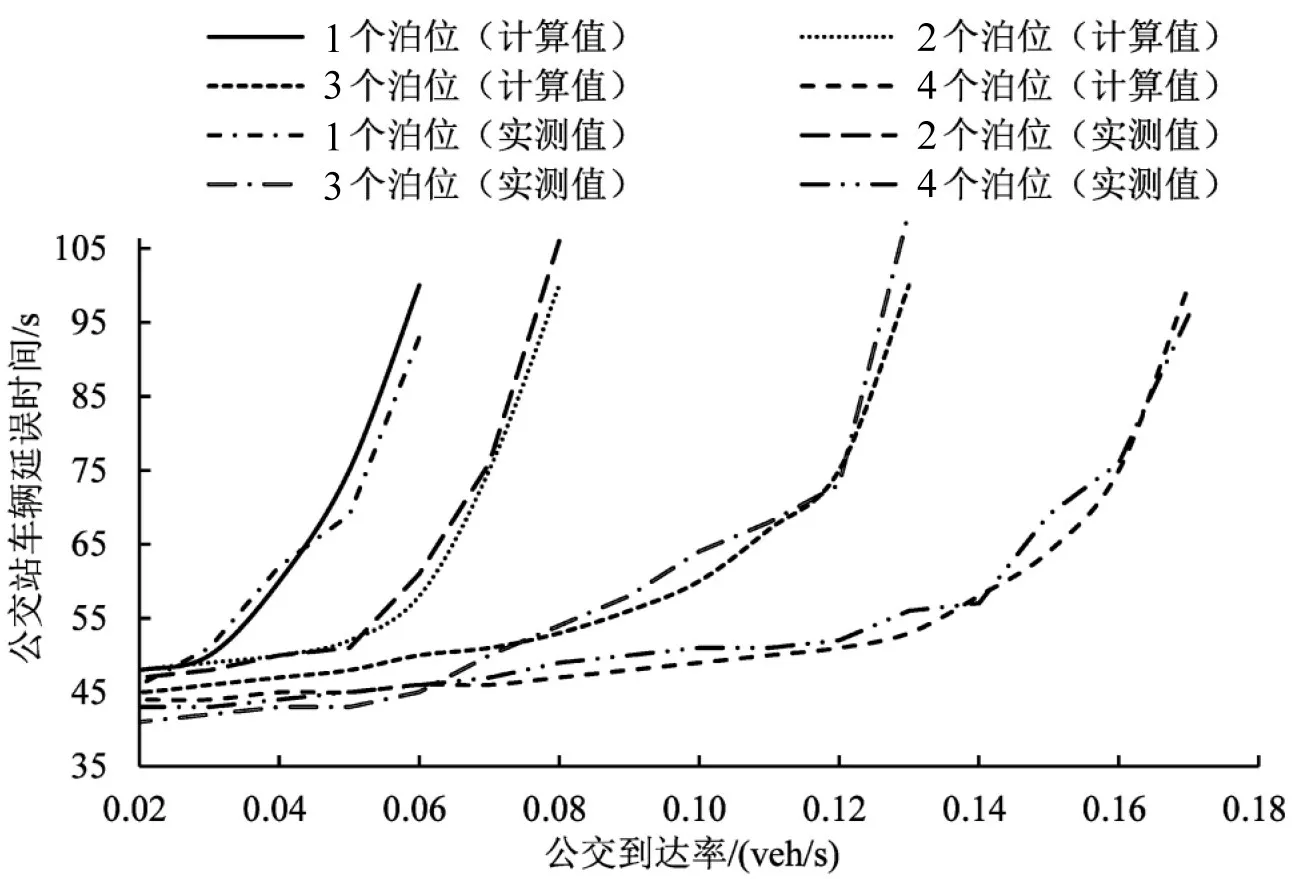
图4 到达率变化下延误计算值与实测值对比Fig.4 Comparison of delay calculation value and measured value under arrival rate change

给定到达率条件下绘制车辆延误随最拥挤车门的上车或下车乘客总数变化的曲线并与实测值对比，如图5所示.公交在站台延误随上下车乘客数增大呈对数函数增大趋势，且不同泊位数下延误曲线接近平行，模型计算值与实测值相对贴合.

给定到达率条件下绘制车辆延误随相邻车道流量的变化曲线并与实测值对比，如图6所示.

公交在站台延误随相邻车道流量增大呈开口向上的抛物线增大趋势，当相邻车道车流量在0～635 veh/h时，车辆延误相近，这是因为公交试图成功的概率较大而汇流延误较小；当流量超过635 veh/h时，延误增长速度越来越大，原因是公交汇流成功概率变小，即公交需要多次尝试后才能成功汇入车流.模型计算值与实测值误差较小，验证模型的有效性和适用性.

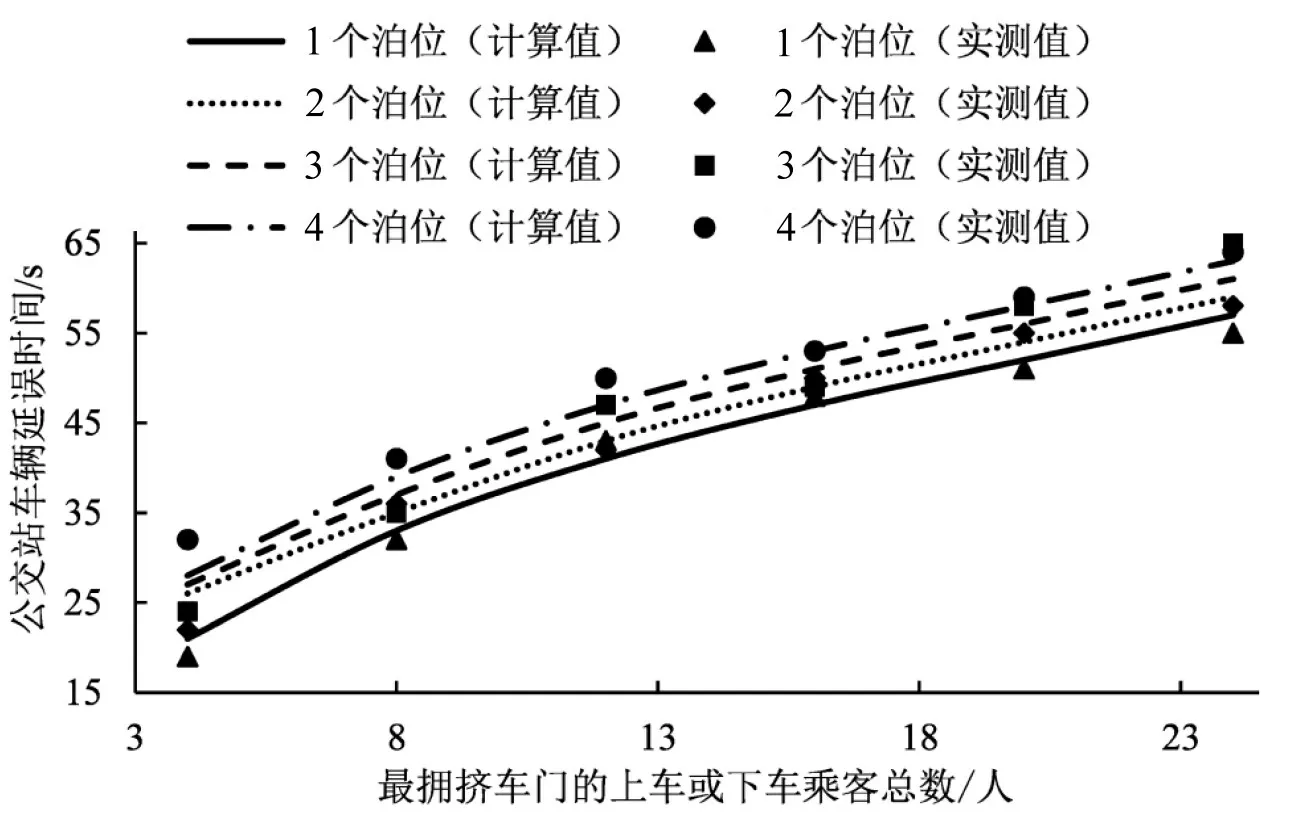
图5 上下车乘客数变化下延误计算值与实测值对比Fig.5 Comparison of delay calculation value and measured value under change of passenger number on and off the bus

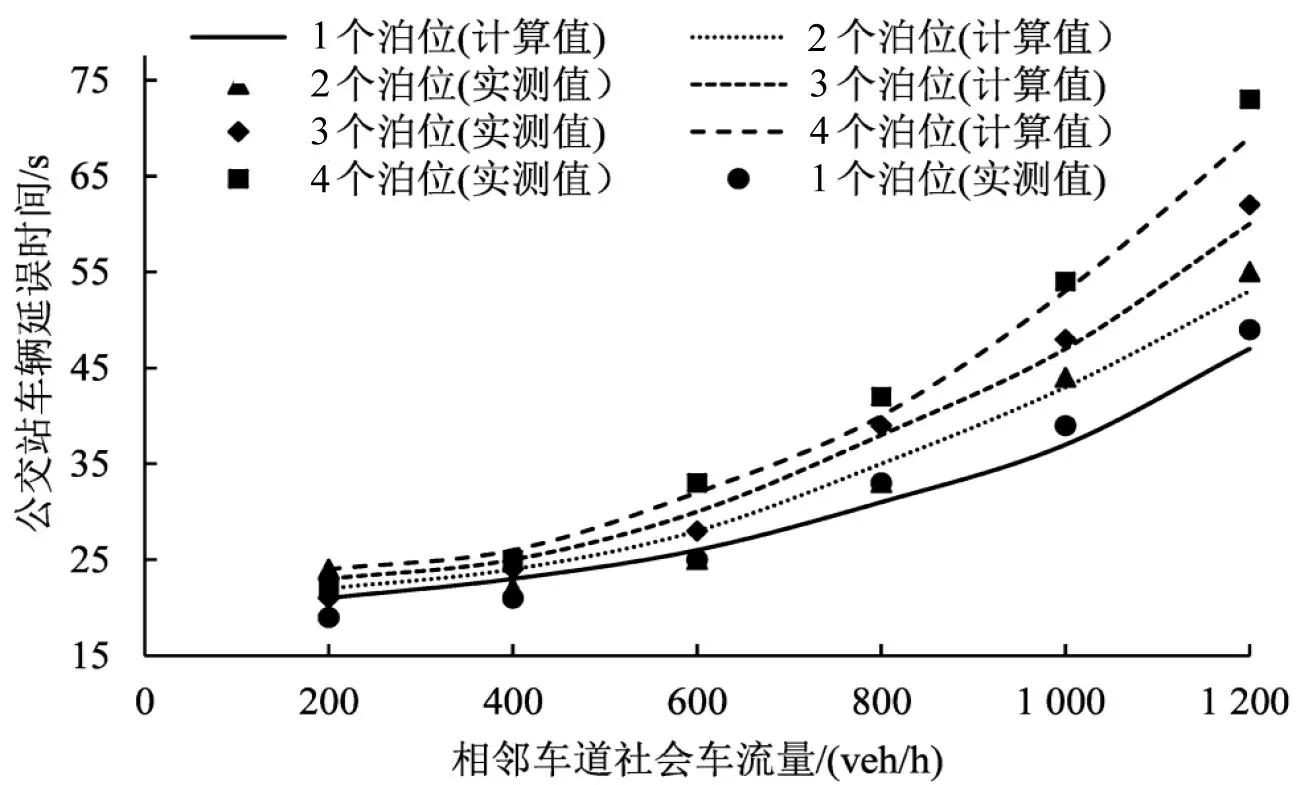
图6 相邻车道流量变化下延误计算值与实测值对比Fig.6 Comparison of delay calculation value and measured value under traffic changes of adjacent lanes

5 结 论

(1)把公交进站排队、汇流等待和停靠服务结束时后车需不需等待的状态进行0-1分类.将影响公交站车辆延误的主要因素分为上下车乘客数、有效泊位数、相邻车道流量和公交到达率.

(2)基于公交在站台微观和时空运行特性，构建进站、停靠和出站延误时间模型，推导出单泊位和多泊位公交站的延误时间模型，并将模型应用到实例中进行模型验证和数值分析.

(3)结果表明：公交在站台延误随公交到达率增大呈指数增长趋势；随上下车乘客数增大呈对数函数增大趋势；随相邻车道流量增大呈开口向上的抛物线增大趋势.

(4)本文未考虑停靠组织策略不同和其它因素对模型产生影响，未来需进一步研究.