隐形矫治方案中的牙齿运动路径规划方法研究
2020-09-01李占利刘童鑫李洪安孙志浩
李占利,刘童鑫,李洪安,孙志浩
隐形矫治方案中的牙齿运动路径规划方法研究
李占利,刘童鑫,李洪安,孙志浩
(西安科技大学计算机科学与技术学院,陕西 西安 710054)
针对隐形矫治方案制定过程中传统牙齿运动路径规划方法准确度及效率低下问题,根据牙颌评价参数提出新的目标函数,再以传统的人工蜂群算法(ABC)为基础,通过外部存储存放Pareto解集,然后以改进的Harmonic距离对Pareto解集进行更新,从而提高种群的多样性。随后通过Slerp球面线性插值以及线性插值获取牙齿运动路径初始值,与人工蜂群算法中的初始食物源生成方式相结合,生成更好的食物源。通过改进后的人工蜂群算法采用优先级方案对新目标函数进行优化,得到牙齿的无碰撞运动路径。通过验证本文方法的矫治方案效果,并与传统目标函数进行比较,结果表明目标函数可以生成更符合临床治疗要求的矫治方案,改进ABC算法相比基本ABC能够获得更优的路径,缩短了矫治阶段数,具有实用价值。
隐形矫治;路径规划;人工蜂群算法;多目标优化
无托槽隐形矫治技术作为一种新型口腔正畸技术,相对于传统矫治技术有着便于拆卸、透明美观、干净卫生的优势,在正畸治疗中很受欢迎[1]。随着计算机辅助设计与口腔正畸学的不断发展与融合,使得隐形矫治计算机辅助系统成为研究热点[2]。在隐形矫治过程中,由牙医根据病人的畸形类型以及病人的诉求进行矫治方案的规划,即牙齿运动路径上关键中间位置的确定,然后将方案通过隐形矫治系统可视化,并将各阶段方案的变化展示给病人,病人同意后进行各阶段矫治器母模的加工[3]。
目前,牙齿运动路径规划局限于交互式手动排列,操作如下:
(1) 选定合适的牙弓曲线模型;
(2) 记录牙齿的初始坐标与理想位置坐标;
(3) 依照牙弓曲线,采用虚拟正畸软件对牙齿进行手动平移、旋转等操作,设计牙齿的运动路径。
交互式手动规划效率低、误差大、精度不够,而且会因为视觉误差影响最终结果。
针对上述问题,部分学者做出了自动化牙齿路径规划方法。王先泽等[4]提出基于粒子群(particle swarm optimization,PSO)的自动化规划方法,其针对手动交互效率不高的缺点,以每颗牙齿选取的特征点到标准牙弓曲线的距离和作为目标函数,以牙齿间的间距作为约束条件,实现了对牙齿路径的自动规划,但未考虑牙齿旋转角度的因素;MOTOHASHI[5]以牙弓线牵引的方式实现了牙齿运动路径规划,但未考虑如病人牙列拥挤,可导致牙齿间发生碰撞,实际效果不好的特殊情况;杨光[6]以牙齿移动量及旋转量为目标函数,通过约束条件,以A*算法进行优化求解牙齿运动中间位置,从而获取牙齿运动路径,目标函数中的旋转量只考虑了旋转角,未考虑轴倾角及转矩角;张筱[7]提出单颗牙齿分别规划的方法,并在牙齿移动规划过程中加入了碰撞检测,得到牙齿正畸路径规划方法的可视化结果,因牙齿运动是多个牙齿同时移动的,可能会发生碰撞。
牙齿运动是一个在三维空间中,涉及到平移、旋转等多方面运动状态的过程。在前人的研究中,由于运动过程中目标函数的不足或是算法性能原因,使得规划效果并不理想。针对传统交互式牙齿路径规划方式以及目前自动化牙齿路径规划方式中的缺陷,根据牙颌测量方法标准,提出更全面的参数目标函数,然后以传统人工蜂群算法为基础,通过自适应罚函数处理约束问题,以外部存储的方式存放Pareto解集,通过改进的Harmonic距离对解集进行更新,提高种群分布性。然后通过插值方法获取牙齿运动理想路径,结合人工蜂群算法的初始化过程,生成更好的初始食物源。最后以改进后的人工蜂群算法对牙齿依照优先级策略进行路径规划。最后通过实验对本文改进方法进行验证及对比,结果表明,该方法规划出的路径更加精准,牙齿运动代价更小。
1 数学模型
1.1 牙齿矫治方案定义
在牙齿矫治之前,医生会根据患者的错颌类型、年龄以及个人诉求为患者规划正畸方案,然后将整个矫治过程用计算机动画进行模拟,记录牙齿关键中间位置,也就是矫治过程中牙齿运动的路径点,并将其展示给患者,记录得到的关键中间位置,结合3D打印技术,制作每一阶段的隐形矫治器。所以,在牙齿矫治方案中,关键的技术点在于规划牙齿运动的路径。对牙齿运动路径规划方案的评价是一个综合了数学计算、计算机技术等多个方面的复合分析过程,其本质就是综合了牙科标准和生理限制对牙齿运动路径的准确性、时效性、经济性以及美观程度等方面进行评价。
1.2 矫治方案评价参数
1.2.1 Spee曲线和牙列拥挤度
Spee曲线[8](下颌牙列的纵颌曲线)是连接下颌切牙的切缘、尖牙的牙尖、前磨牙的颊尖以及磨牙的近远中颊尖的连线,可反映下颌平整度。文献[9]指出,越是理想的牙颌形态,其Spee曲线就越平滑。在正畸学中,牙列拥挤度能直接决定是否需要进行拔牙或扩弓治疗,如果患者牙列过于拥挤,则更易碰撞,与矫治器附件互相作用,导致牙齿无法到达理想位置,使矫治方案无法准确实施,所以牙列拥挤度是矫治方案效果的评价依据。牙列拥挤度与Spee曲线有密切的关系,Spee曲线越平滑,牙列的拥挤度会变大,引起如牙齿向唇侧突出的问题。一般情况下,每平整1 mm的Spee曲线,需要缩小1 mm的牙弓间隙。所以Spee曲线深度和牙列拥挤度应该控制在一个平衡的范围内,过度松散及拥挤均会给病人带来不适。Spee曲线及咬合面关系如图1所示。
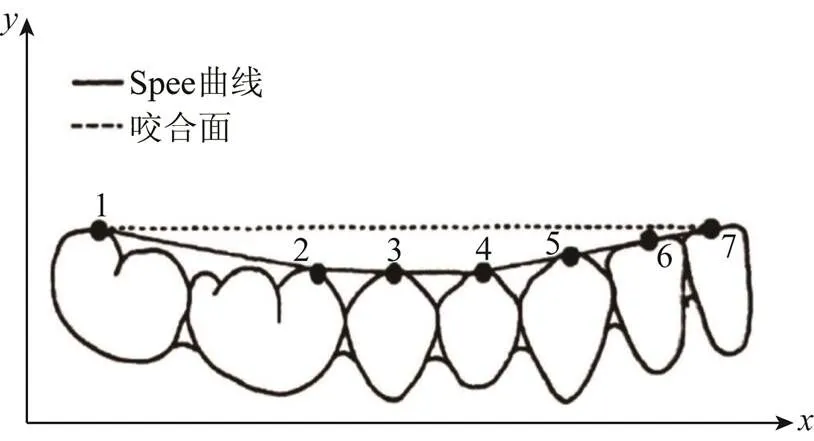
图1 Spee曲线
1.2.2 牙弓对称性
牙弓对称性[10]主要包含:①上下颌关于咬合面的对称性;②同一牙列两侧牙齿关于牙弓中轴线的对称性。牙弓对称性如图2所示。
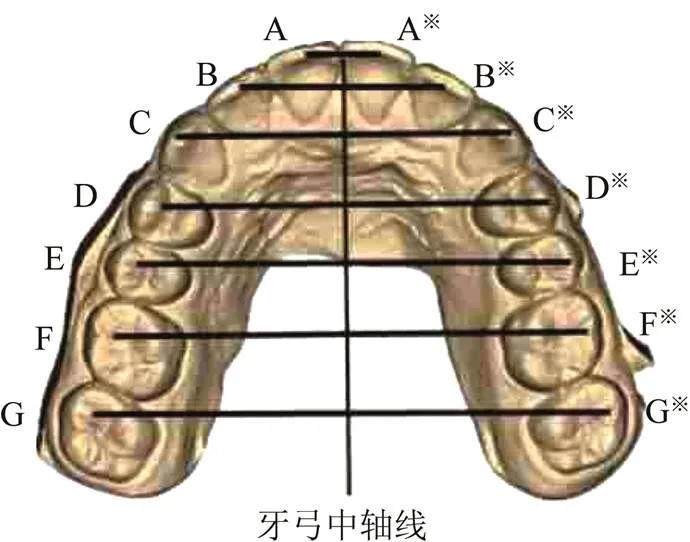
图2 牙弓对称性
将上颌牙弓的中轴线投影到咬合面上,该投影与下颌中轴线方向向量之间的夹角越小则表明上下牙弓越对称。
两侧牙齿之间的对称性则分别在各自所在牙弓进行,以上颌为例,将磨牙的近中舌侧牙尖点、前磨牙的舌侧牙尖点以及尖牙的牙尖点投影到咬合平面,向上颌牙弓中轴线作垂线,线段长度代表牙齿到中轴线的距离,通过测量两侧牙齿到中轴线的距离,其差值越小则越对称。
1.3 正畸参数计算
1.3.1 Spee曲线深度
口腔学将牙尖点中最低的点到第二磨牙远中颊尖与中切牙最高点所构成的直线距离,称为Spee曲线深度,即
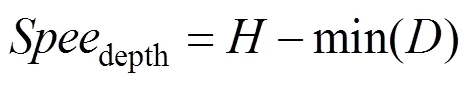
其中,为咬合面的高度;为牙尖点高度,取最小值。为了使Spee曲线尽量平滑,式(1)需取极小值。
1.3.2 牙列拥挤度
牙列拥挤度,是指牙弓原本应有的长度与现有长度之差。牙弓应有长度代表所有牙齿宽度之和。牙弓现有长度是指当前牙弓线长度。
当前牙弓线长度可以用四次二维曲线来表示,将牙齿特征点投影到咬合面,然后用最小二乘法拟合出该曲线,即

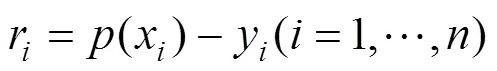

则可得到牙弓线现有长度为
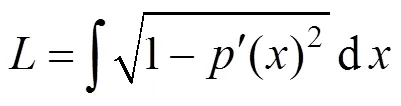
牙列拥挤度为

其中,W为第颗牙齿的宽度。
1.3.3 牙弓对称度
分析上下颌两侧同名牙齿之间的对称度,将两侧牙尖到中轴线的距离差值的绝对值进行累加,再除以牙齿的对数,即可求出牙弓对称度[11],即

其中,D为观察者左侧的牙齿到中轴线的距离;D为观察者右侧的牙齿到中轴线的距离;为牙齿数量,/2则是牙齿的总对数;当越小,则两侧牙齿的对称度越高。
1.3.4 牙齿移动量与旋转量
假设分割后的牙齿数量为,则颗牙齿中的每一颗从初始位姿到最终位姿都会构成一系列的离散点,这一系列的离散点即为路径点。其中每个路径点就是每一矫治阶段中该牙齿所在的位置,路径点的总数需要在路径规划前确定,在每一阶段中,牙齿的运动状态又可分为平移与旋转。
最终颗牙齿的正畸方案为

设第颗牙齿的运动函数为

其中,,,分别为第颗牙齿在局部坐标系中沿3个方向的移动量;,,分别为牙齿的转矩角、轴倾角、旋转角。
最终的目标转化为对下列的问题求解
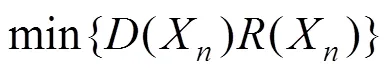
其中
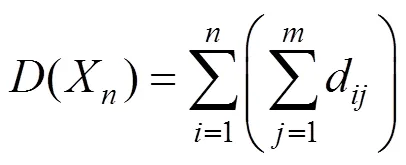
其中,d为牙齿在第阶段的移动量,即

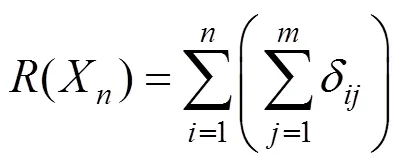
且,为牙齿在第阶段的旋转量。
1.4 目标函数
经过上述评价参数的建立,得到需要最优化的目标函数集合

1.5 约束条件
1.5.1 碰撞检测
在牙齿移动过程中,为避免同步移动时的干涉问题,故要在规划过程中对牙齿进行碰撞检测,即

其中,c为当前第颗牙齿是否在第阶段与相邻牙齿发生碰撞,默认值为0,发生碰撞则为1;为判断当前路径是否发生碰撞,当=1为发生碰撞。
1.5.2 移动量和旋转量
在矫治过程中,牙齿一次平移量与旋转量不能过大,有


其中,0取0.5 mm;0取3°。
1.5.3 牙齿间距
牙齿在沿正畸路径移动时需要考虑到牙齿间距,相邻牙齿的间距不大于0.5 mm,即
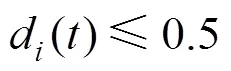
其中,d()为第与第+1颗牙间距。
由上文可知,牙齿运动路径规划问题的最终求解为

其中,()为需要最优化的目标函数集合;()为约束函数集合,式(18)要在满足约束条件的情况下取得目标函数最小值,因此牙齿运动路径规划问题实际上是一个带约束条件的多目标优化问题。
2 基于人工蜂群算法的约束多目标优化
2.1 基本人工蜂群算法
为了解决全局优化问题,KARABOGA[12]提出了人工蜂群(artificial bee colony,ABC)算法。其是根据蜜蜂采蜜行为提出的一种优化方法,可通过直接比较参数的优劣来实现局部寻优,快速收敛,从而迅速找出全局最优值。
ABC算法将蜂种按分工分为雇佣蜂、观察蜂和侦察蜂,其中雇佣蜂与食物源对应,一个食物源为一个可能的解决方案,花蜜量代表该解决方案对应的目标函数值。观察蜂以适应度选择食物源,经过一定数量的选择(控制参数),若食物源得不到更新,则弃之,该雇佣蜂变为侦查蜂,再次搜寻食物源,且此侦查蜂又变回雇佣蜂。许多研究者利用人工蜂群算法易用、高效的特点,将其应用于路径规划领域。初始人工蜂群算法的步骤如下:
步骤1.初始化。在初始化阶段,假设蜂群规模为,则侦察蜂与观察蜂的数量均为=/2,首先由侦察蜂随机生成个食物源,即

其中,x为第个食物源的位置,=1,2,...,,=1,2,...,,为优化问题的维数;ub和lb分别为该食物源第维变量可取的上界和下界。
对每个初始食物源计算适应度,并记录其适应度值设置为,并将最优食物源记为best,初始化当前食物源开采次数变量()=0,适应度为

步骤2.循环以下4步,直至到达终止条件。
(1) 雇佣蜂搜索。雇佣蜂在当前食物源周围搜索新的食物源,搜索策略为

其中,x为当前食物源的一个相邻食物源,通过计算新食物源的适应度并与当前食物源适应度进行比较,选择适应度较高的食物源,即

若成功更新了当前食物源,则将新食物源()置零,否则()自增一次。
(2) 观察蜂评价。观察蜂可根据食物源的适应度计算食物源的跟随概率p

获得p后,利用轮盘赌机制决定当前食物源是否更新,若更新则按照雇佣蜂策略局部搜索新食物源。
(3) 侦察蜂搜索。对当前食物源的()进行判断,当超过搜索次数上限时,则按照式(19)全局搜索新的食物源来代替当前的枯竭食物源。
(4) 记录最好食物源。通过变量记录当前蜂群中的最大适应度,并与进行比较,且更新

若最好食物源得到更新,则同步更新种群中的最好食物源记录best。
步骤3.当迭代次数超过,输出最终解best。
2.2 算法优化
2.2.1 动态罚函数处理约束问题
KARABOGA和BASTURK[13]通过Deb准则解决了约束问题,但也破坏了种群的多样性,不利于算法收敛。本文提出使用罚函数将约束优化问题转化为无约束优化问题,根据牙齿运动约束量,罚函数为

其中,g()为小于号约束条件;h()为等号约束条件;H(g())和H(h())为指示函数,分别为

其中,为惩罚系数,其值通过自适应方法来选取,即


2.2.2 改进的Harmonic距离排序构造Pareto解集
本文通过外部存储来存放Pareto解集,其计算及更新方式基于拥挤距离排序方法进行优化。拥挤距离排序方法在NSGA-Ⅱ[14]算法中被提出,用于描述某一最优解周围分布其他解的密度,便于排除冗余度大的解,保留其他具有多样性的解,从而确保全局寻优能力。文献[15]指出,与拥挤距离相比,Harmonic距离用来反映个体间的拥挤程度效果更好,其表达式为

其中,为种群规模;d,j为个体x与x在目标空间上的欧氏距离。


拥挤密度改进方法一方面减少了计算量,提高了算法效率,另一方面计算拥挤距离时也考虑到了距离较远的个体,不影响解集的分布性,还考虑了当前精英个体的影响,降低了较差个体带来的影响。因此,改进的Harmonic拥挤距离计算在提高效率的同时减少了不良影响,能准确反映个体的分布情况,兼顾了种群多样性。
综上,本文Pareto解集更新方式为:设外部存储Pareto解集的容量为。
步骤1. 在每个优化目标上,按目标函数值对当前所有个体进行升序排列,选择Pareto等级较优的个体放入中,若容量超出限制,则跳至步骤2,否则继续计算直至遍历结束;
步骤2.利用式(29)计算目前解集中最劣Pareto等级个体的拥挤距离并降序排列,删除拥挤距离较小的个体,如果有2个或更多最小解,随机移除一个。
3 牙齿运动路径规划
3.1 结合牙齿运动路径规划的初始食物源生成
在人工蜂群算法中,初始化阶段是由侦察蜂全局生成初始食物源。对于牙齿运动路径规划而言,最优路径实际上是直接从起始位姿平移旋转到目标位姿,是理想无碰撞情况下的路径,而实际正畸过程中,会出现牙齿间的碰撞、约束及运动量约束等问题,因此需要在理想路径的基础上优化出无碰撞、满足约束的路径。基于此,需首先获取理想状态下的牙齿路径,并以此作为初始食物源,然后结合人工蜂群算法对路径进行优化。
3.1.1 旋转量插值


图3 线性插值
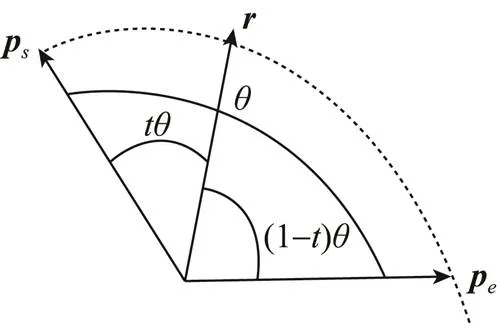
图4 球面插值
在牙齿运动路径规划过程中,由于正畸力不便于控制,所以假设牙齿的角速度恒定,本文采用球面线性插值(spherical linear interpolation,Slerp) 来进行牙齿旋转量插值,即
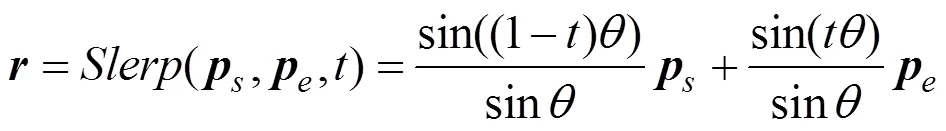
3.1.2 平移量线性插值
在欧氏空间中,任意2点间的最短距离为 2点的直线距离,因为牙齿的平移量只需根据上文中移动量约束进行均匀插值,可分为若干正畸阶段,如图5所示,其中0i为牙齿初始位置;C为牙齿目标位置。

图5 平移量插值
3.1.3 初始食物源生成
在获取了牙齿旋转量及平移量插值后,也就获得了牙齿在理想情况下的运动路径,图6为侧切牙插值结果。此时结合人工蜂群算法中的侦察蜂搜索策略,以插值路径作为初始值,生成初始食物源,步骤如下:
步骤1.设定牙齿平移步长约束0和旋转步长限制0;
步骤2.根据0和0计算初步正畸阶段数;
步骤3.根据正畸阶段数对旋转量进行Slerp球面插值,对平移量进行线性插值,获取初始值;
步骤4. 由侦察蜂算法根据初始值生成个初始食物源。
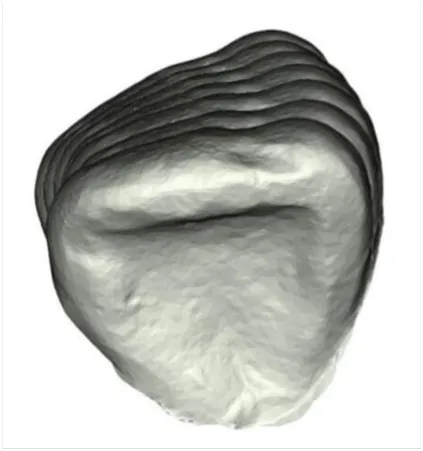
图6 侧切牙插值结果
将人工蜂群算法的初始化方法与牙齿运动理想路径相结合,对搜索方向加以引导,加快收敛速率的同时并未改变侦察蜂算法的初衷,确保了食物源的多样性。
3.2 基于优先级策略的牙齿碰撞避免
在正畸过程中,由于牙齿的畸形情况各不相同,且运动状态各异,根据牙齿不同运动状态以及不同的错位情况,将牙齿可能发生碰撞的情况分为图7中的4类情况。
情况1:2颗牙齿相向运动,其牙根交错,此类情况在正畸过程中应该避免牙根的碰撞,主要靠牙冠粘贴附件选择合适的施力方式避免碰撞;
情况2:牙齿朝着同一方向运动,此时为一颗牙齿挡在另一颗前面,且占据了另一颗要去的位置,由于在正畸过程中牙齿是同步移动的,可以优先规划前一颗,再规划后一颗牙齿;
情况3:2颗牙齿朝着相反方向运动,此时主要考虑避免牙冠的碰撞情况;
情况4:已经运动到最终位姿的牙齿占据了其他牙齿的路径,此时被占据路径的牙齿只能绕路以避免碰撞。
通过分析牙齿碰撞情况可以发现,牙齿运动过程的碰撞只发生于相邻牙齿之间,不会与其他的牙齿发生碰撞,因此,可以根据各个牙齿与相邻牙齿的不同情况,制定优先级方案,实现无碰撞的牙齿运动路径规划。
优先级方案在多机器人路径规划的研究中被广泛使用[17],通过为多个运动过程中可能存在冲突的机器人分配运动顺序使其避免冲突,即:首先为每个机器人分配一个优先级,然后按照优先级对机器人遍历,依次为机器人规划路径,避免与工作环境中的静态障碍物和其他机器人发生碰撞。本文参考文献[18],在牙齿运动路径规划策略中引入优先级方案,从而实现无碰撞正畸路径。
3.2.1 优先级算法
牙齿的碰撞只会发生在相邻牙齿之间,因此只需考虑相邻牙齿间的优先级关系,本文采用的牙齿正畸优先级判定算法是通过相邻牙齿的位姿距离来判定牙齿间的优先级,即

其中,L0i_0j中的0为牙齿初始位姿序号,m为牙齿理想位姿序号,i为牙齿序号,j为与i相邻的牙齿;w1,w2为权值,取0.5;为牙齿间的欧氏距离;为牙齿姿态间的四元数距离,越大,表示其角旋转越相似,同理可计算得到2颗牙齿的目标位姿距离Lmi_mj。以2颗牙齿初始位姿距离与目标位姿距离的差值进行判断,当时,牙齿间碰撞会出现情况1或情况3,这2种情况说明2颗牙齿优先级相同,即PMi=PMj;当时,此时为情况2,2颗牙齿运动方向相同,需要判断其位姿前后顺序,分别计算牙齿i的初始位姿到牙齿j的目标位姿距离L0i_mj,以及牙齿j的初始位姿到牙齿i的目标位姿距离L0j_mi,若,则PMi>PMj,否则PMi 通过以上策略,遍历所有牙齿,即可得到牙齿间的优先级关系,其中为牙齿不同的情形分类阈值,为牙齿移动距离阈值,当牙齿移动距离小于时,最后考虑其运动路径。 3.2.2 优先级判定步骤 判定牙齿之间优先级的具体步骤如下: 输入:牙齿初始位姿及目标位姿序列,空的牙齿正畸优先级列表; 步骤1. 依次遍历牙齿; 步骤2. 根据当前牙齿的初始位姿和目标位姿计算其位姿距离0i_mi,若0i_mi≤,则可定义为极小优先级,跳转至步骤1,否则,继续步骤3; 步骤5. 遍历结束,输出。 3.3.1 实际正畸阶段数获取 在生成初始食物源的过程中所获取的正畸阶段数是通过插值所得,考虑的是无碰撞的理想环境。但实际中,牙齿运动很可能会发生碰撞,所以,相较于理想情况,实际规划过程中的牙齿路径点数会发生变化,实际的正畸阶段数也会大于无碰撞情况下的阶段数。 为解决此问题,在雇佣蜂计算适应度函数时,不考虑牙齿移动量和旋转量约束,在整体规划完成后,再对每一阶段的路径点按照平移量和旋转量的约束进行若干个路径点的划分,获取真实情况下的正畸阶段数。如图8所示,点与是2个初始食物源,′和′分别是点和点邻域内的最佳食物源,由于牙齿运动量约束,会判断′与′距离超过约束而放弃这2个食物源,那么就会错过最优值,所以在对食物源进行评价时,不对移动量与旋转量进行约束,而是在规划完成后,按照约束对路径进行划分,如将′′划分为′和′ 2个阶段。 图8 路径点规划示意图 3.3.2 牙齿运动路径规划步骤 根据本文算法,结合正畸优先级、牙齿运动路径规划实际情况,建立牙齿运动路径规划步骤: 输入:待正畸牙齿T初始位姿0i、目标位姿P序列; 输出:各颗牙齿运动路径关键中间位姿解集PA。 步骤1. 通过Slerp球面及平移量插值对每颗牙齿生成平移量插值1i~(m–1)i、旋转姿态插值1i~δ(m–1)i; 步骤2.遍历牙齿,根据优先级方案为牙齿设置优先级,获取牙齿优先级列表; 步骤3. 根据优先级列表,按照优先级顺序对牙齿依次进行路径规划; 步骤4. 初始化参数,主要包括路径点数量、每个食物源搜索最大限制参数、当前迭代次数=0,侦察蜂最大搜索次数,初始种群数量、侦察蜂和观察蜂分别为=/2,外部存储PA; 步骤5. 侦察蜂算法生成初始个食物源,然后转变为雇佣蜂; 步骤6. 初始化当前食物源搜索次数()=0,根据目标函数值计算食物源适应度,将非支配解放入PA中并计算拥挤距离,进行排序; 步骤7. 雇佣蜂局部寻找新的食物源并计算适应度,若优于当前食物源,则更新食物源位置,令次数()=0,更新外部存储PA,否则次数()自增1; 步骤8. 观察蜂计算跟随概率,根据其寻找新食物源,然后转变为雇佣蜂进行局部搜索,计算适应度,判断是否更新,并更新开采次数(),更新外部存储,若()>,则继续步骤9,否则跳至步骤10; 步骤9. 放弃当前食物源并转化为侦察蜂,在决策空间随机产生新的食物源,计算适应度,更新(); 步骤10. 记录食物源,并更新外部存储解集,迭代次数自增1,若>,则输出解集PA,否则跳转至步骤8。 3.3.3 算法流程图 算法流程如图9所示。 图9 牙齿运动路径规划流程图 实验中共用20口患者牙齿数据进行了路径规划,其中选取患者为18岁男性为样例,展示执行优化人工蜂群算法后所形成的牙齿矫治方案以及牙齿运动前后位置对比。 如图10所示,以上颌为例,总共分为39个阶段,算法中设置为200次,设置为 4 000次,种群大小为28。筛选出解集中的非支配解形成牙齿运动路径,展示其中9个中间阶段。图中牙齿上的线段为每颗牙齿的特征线段,可以看出,经过39个阶段的平移与旋转,各颗牙齿逐渐移动至理想牙弓线上,牙齿特征线段也逐渐平滑(图中被椭圆及矩形标注的牙齿)。图11展示了各颗牙齿的位姿变化。可以看出,上颌左侧中切牙(牙号11)的旋转量最大,旋转角为顺时针31.3°,两侧侧切牙(牙号12,22)移动量较大,分别为2.393 mm与2.418 mm。此例主要移动量集中在前牙、尖牙及前磨牙,而两侧后磨牙移动较少,在实际正畸治疗中对后磨牙的矫正难度较大。 图10 牙齿关键中间位置 牙齿移动前后对比如图11所示,仅以牙齿偏移量为目标函数的规划结果参数对比见表1,在优化ABC算法中,由于对解集的更新方式进行了改进,提高了种群的分布性,可以获得更好的解,与基本ABC算法相比,能够以更小的牙齿移动代价实现牙齿运动路径规划,到达理想位姿所需的矫治阶段数也更少,从而缩短矫治周期,减轻患者负担。从表2中可以看出,在目标函数中加入了正畸参数之后,由于优化目标变多,会略微增加牙齿的偏移量,也会稍微增加矫治阶段数。但从表3的牙颌参数中可以看出,牙弓对称度、牙列拥挤度以及Spee曲线深度都有了很好的改善,正畸方案可取得更好的效果,可以说明在目标函数中加入正畸评价参数有利于提高矫治方案的准确性和实用性。与此同时,优化ABC算法的结果优于基本ABC算法,证明本文在提升了ABC算法的种群多样性之后,能够获得更好的优化结果。 图11 牙齿移动前后对比 表1 仅考虑偏移量的规划结果 表2 考虑正畸评价参数的规划结果 表3 牙颌参数对比 本文基于传统的隐形矫治方案生成方法,提出了新的目标函数,以Spee曲线深度、牙列拥挤度、牙弓对称度以及牙齿的偏移量为参数,减少了牙齿偏移量,在人工蜂群算法的基础上加入搜索系数,提高了算法的效率,再对牙齿运动路径进行规划。最后在仿真软件进行测试,并与其他方法进行对比,结果显示本文方法能较快生成较高准确度的运动路径,减少牙齿总的偏移量,生成的方案结果更接近理想牙颌,有效缩短矫治周期,具有实用意义。 [1] 卢海丽, 康娜. 无托槽隐形矫治器与固定矫治器对正畸患者牙周健康影响的研究现状和进展[J]. 口腔医学研究, 2019, 35(7): 625-628. LU H L, KANG N. Research progress and current situation of influence of Invisalign system and fixed appliances on periodontal health[J]. Journal of Oral Science Research, 2019, 35(7): 625-628 (in Chinese). [2] 范然, 钮叶新, 金小刚,等. 计算机辅助牙齿隐形正畸系统[J]. 计算机辅助设计与图形学学报, 2013, 25(1): 81-92. FAN R, NIU Y X, JIN X G, et al. Computer aided invisible orthodontic treatment system[J]. Journal of Computer-Aided Design &Computer Graphics, 2013, 25(1): 81-92 (in Chinese). [3] GERARD BRADLEY T, TESKE L, ELIADES G, et al. Do the mechanical and chemical properties of InvisalignTMappliances change after use? A retrieval analysis[J]. The European Journal of Orthodontics, 2016, 38(1): 27-31. [4] 王先泽, 李忠科, 马亚奇, 等. 一种基于PSO的自动化排牙方法[J]. 计算机工程与应用, 2012, 48(5): 211-212, 238. WANG X Z, LI Z K, MA Y Q, et al. Method of arranging teeth automatically based on PSO[J]. Computer Engineering and Applications, 2012, 48(5): 211-212, 238 (in Chinese). [5] MOTOHASHI N. A 3D computer-aided design system applied to diagnosis and treatment planning in orthodontics and orthognathic surgery[J]. The European Journal of Orthodontics, 1999, 21(3): 263-274. [6] 杨光. 牙齿矫正中牙齿移动的仿真和优化方法研究[D].西安: 西安科技大学, 2011. YANG G. Research on simulation and optimization method for tooth movement in virtual orthodontics[D]. Xi’an: Xi’an University of Science and Technology, 2011 (in Chinese). [7] 张筱. 牙齿正畸路径规划方法研究及可视化开发[D]. 济南: 山东大学, 2016. ZHANG X. Research on teeth orthodontic movement path planning and visual development[D]. Jinan: Shan Dong University, 2016 (in Chinese). [8] REKOW E D, ERDMAN A G, RILEY D R, et al. CAD/CAM for dental restorations-some of the curious challenges[J]. IEEE Transactions on Biomedical Engineering, 1991, 38(4): 314-318. [9] 龚诚, 闻娟, 李佳岭, 等. Spee曲线和拥挤度对口腔正畸模型2D与3D测量法的影响[J]. 口腔医学研究, 2018, 34(6): 657-661.GONG C, WEN J, LI J L, et al. Influence of Spee’s curve and crowding on 2D and 3D measurement of orthodontic model[J]. Jouranal Oral Science Research, 2018, 34(6): 657-661 (in Chinese). [10] STANLEY B, WILLAM P, DANA E, et al. The form of the human dental arch[J]. Angle Orthod, 1998, 68: 29-36. [11] 聂琼, 林久祥. Angle各类错(牙合)及正常(牙合)牙弓对称性分析与比较[J]. 中华口腔医学杂志, 2000, 35(2): 105-107. NIE Q, LIN J X. Analysis and comparison of dental arch symmetry between different Angle’s malocclusion categories and normal occlusion[J]. China Jouranal Stomatol, 2000, 35(2): 105-107 (in Chinese). [12] KARABOGA D. An idea based on honey bee swarm for numerical optimization[R]. Kayseri: Erciyes University, 2005. [13] KARABOGA D, BASTURK B. Artificial bee colony (ABC) optimization algorithm for solving constrained optimization problems[C]//Lecture Notes in Computer Science. Heidelberg: Springer, 2007: 789-798. [14] DEB K, AGRAWAL S, PRATAP A, et al. A fast elitist nondominated sorting genetic algorithm for multi-objective optimization: NSGA-II[C]//International Conference on Parallel Problem Solving From Nature. Heidelberg: Springer, 2000: 849-858. [15] HUANG V L, SUGANTHAN P N, QIN A K. Multi-objective differential evolution with external archive and harmonic distance-based diversity measure[R]. Singapore: Nanyang Technological University, 2005. [16] 毕晓君, 张磊, 肖婧. 基于双种群的约束多目标优化算法[J]. 计算机研究与发展, 2015, 52(12): 2813-2823. BI X J, ZHANG L, XIAO J. Constrained multi-objective optimization algorithm based on dual populations[J]. Journal of Computer Reasearch and Development, 2015, 52(12): 2813-2823 (in Chinese). [17] 马勇. 多移动机器人路径规划研究[D]. 武汉: 华中科技大学, 2012. MA Y. Research on path planning of multi-mobile robots[D]. Wuhan: Huazhong University of Science and Technology, 2012 (in Chinese). [18] 付敬鼎. 隐形矫治技术中的正畴路径规划研究[D]. 西安: 西安科技大学, 2018. FU J D, Research on the path planning for orthodontics in invisalign technique[D]. Xi’an:Xi’an University of Science and Technology, 2018 (in Chinese). Research on path planning of teeth movement in invisible orthodontic LI Zhan-li, LIU Tong-xin, LI Hong-an, SUN Zhi-hao (College of Computer Science and Technology, Xi’an University of Science and Technology, Xi’an Shaanxi 710054, China) Aimed at solving low efficiency and accuracy of path planning of teeth movement in invisible orthodontic schedule, a new method was proposed. First, a new objective function was proposed based on the evaluation parameters of teeth and jaws. Based on the traditional artificial bee colony algorithm (ABC), Pareto solution sets were stored through external storage, and then the Pareto solution set was updated by the improved Harmonic distance, thus diversifying the population. Then, the Slerp spherical linear interpolation and linear interpolation were used to obtain the initial value of the tooth movement path, which was combined with the initial food source generation method in the artificial colony algorithm to generate a better food source. Finally, the new objective function was optimized by the priority scheme of the optimized ABC, leading to the collision-free path for the teeth movement. The experiment showed the effect of the proposed method and compared it with the traditional objective function. The results show that the proposed objective function can generate a more suitable schedule for clinical orthodontic. The improved algorithm can result in a better path and reduce the number of orthodontic stages, and is of practical value. invisible orthodontic; path planning; artificial bee colony algorithm; multi-objective optimization TP 391 10.11996/JG.j.2095-302X.2020040556 A 2095-302X(2020)04-0556-11 2019-12-30; 2020-04-14 14 April, 2020 30 December, 2019; 陕西省自然科学基础研究计划项目(2019JM-162;2019JM-348);西安科技大学博士启动金项目(2019QDJ007) Natural Science Basic Research Plan in Shaanxi Province (2019JM-162; 2019JM-348); Ph.D Research Startup Foundation of Xi’an University of Science and Technology (2019QDJ007) 李占利(1964–),男,陕西周至人,教授,博士,博士生导师。主要研究方向为计算机图形图像处理。E-mail:lizl@xust.edu.cn LI Zhan-li (1964–), male, professor, Ph.D. His main research interests cover computer graphics, image processing. E-mail: lizl@xust.edu.cn 李洪安(1978–),男,山东武城人,副教授,博士,硕士生导师。主要研究方向为计算机图形图像处理。E-mail:an6860@126.com LI Hong-an (1978–), male, associate professor, Ph.D. His main research interests cover computer graphics, image processing. E-mail: an6860@126.com3.3 牙齿运动路径规划
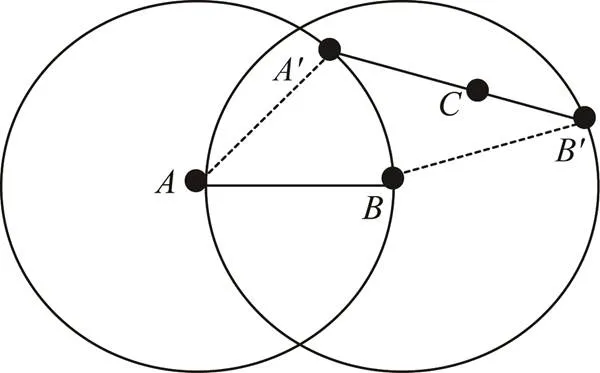

4 实验结果及分析
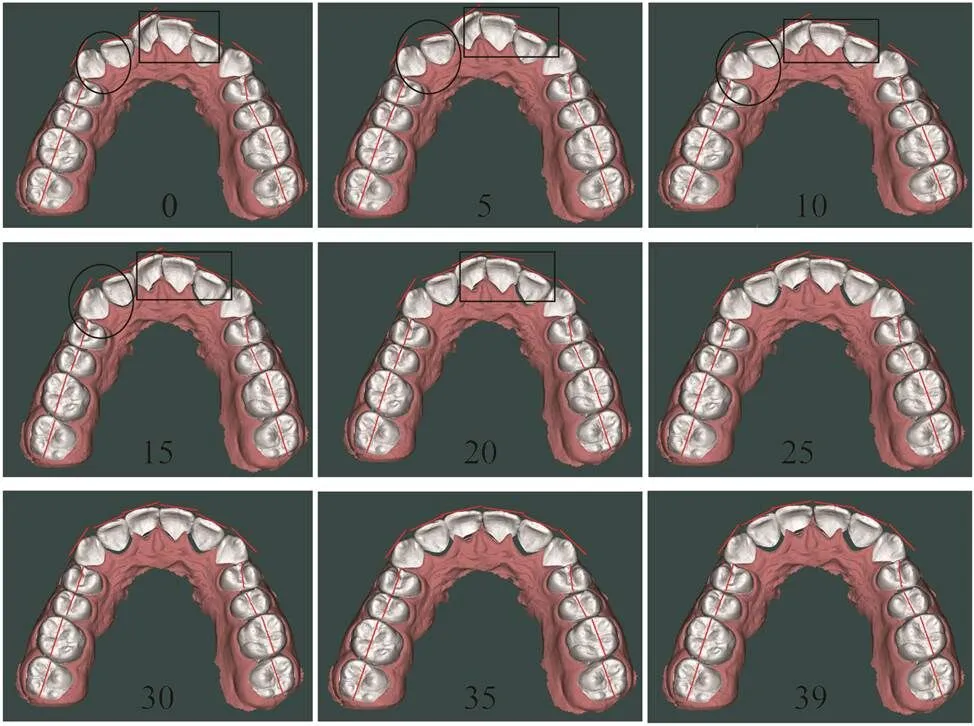
4.1 牙齿运动路径规划结果
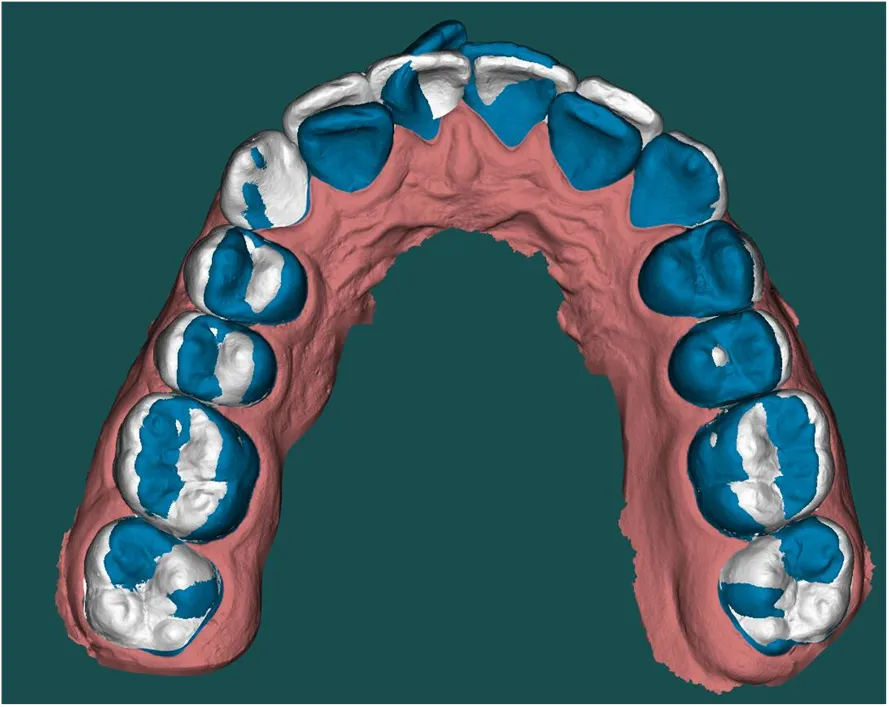
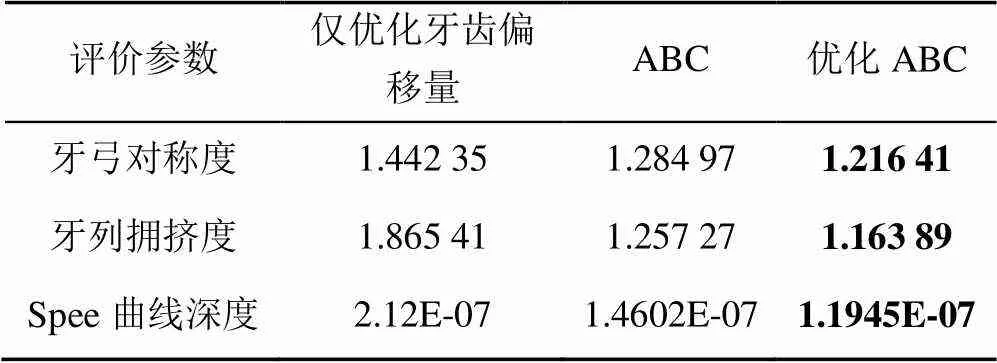
4.2 不同目标函数实验结果对比

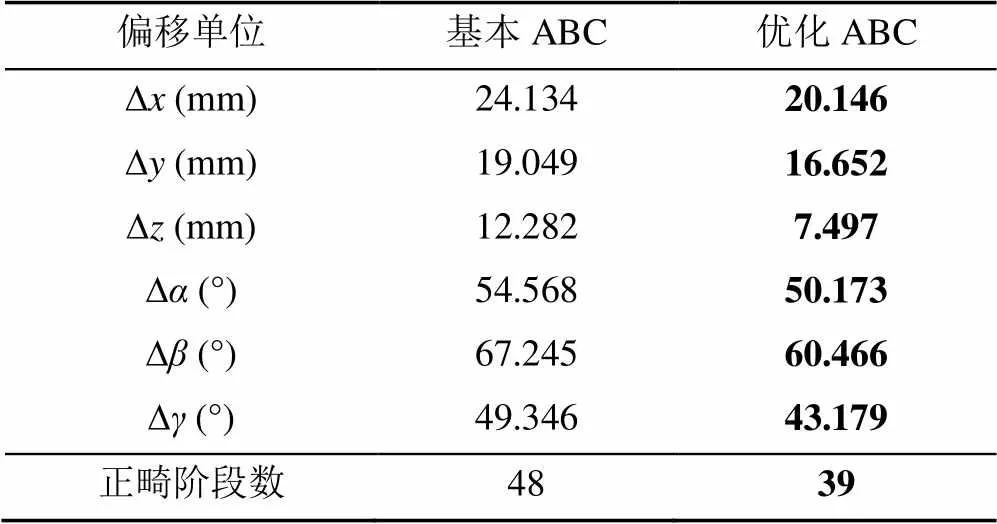
5 结束语
