基于3D-Harris与FPFH改进的3D-NDT配准算法

范 强，刘 鹏，杨 俊，周沛希

基于3D-Harris与FPFH改进的3D-NDT配准算法

范 强1，刘 鹏1，杨 俊2，周沛希1

(1. 辽宁工程技术大学测绘与地理科学学院，辽宁 阜新 123000；2. 辽宁师范大学城市与环境学院，辽宁 大连 116029)

针对传统点云配准三维正态分布变换(3D-NDT)、迭代最近点(ICP)算法在未给定初始配准估计的情况下配准效果不佳、配准时间长、误差较大的缺陷，提出了精准且相对高效的点云匹配算法。首先，运用3D-Harris算法识别每一幅点云的关键点，并以此为基本点建立局部参考框架，计算快速点特征直方图(FPFH)描述子；之后，使用最小中值法(LMeds)中的对应估计算法排除不准确的点对应关系，得到含有对应三维特征关系的特征点对。计算粗配准所需的变换矩阵，完成初步匹配。随后，根据3D-NDT算法将点云数据空间体素化，运用概率分布函数完成最终的点云进行精确地匹配。使用改进配准将3组分别从网络下载的较少噪声、大规模与Kinect V2.0采集的较多噪声、大规模的2组重叠度不同的点云数据匹配到同一个空间参考框架中，并通过精度分析对比经典3D-NDT，ICP等算法。实验结果证明，该算法在迭代次数较低时，可使室内场景点云数据完成精度较高的配准且受噪声影响较小，但如何将算法的复杂度适当降低，缩短配准时间需要更进一步的研究。

三维正态分布变换；3D-Harris特征点；快速点特征直方图；最小中值法；点云配准

近年来，空间三维信息采集技术的发展和点云数据处理领域逐渐成为研究热点[1]。以及应运而生的Kinect等一系列传感器[2]，使得对三维影像的研究更加方便、快捷。在三维数据的各领域研究中，对同一区域不同角度或多测站间点云的配准是整个研究领域中重要的环节之一。快速精准的点云匹配算法可以为三维重建、识别地物、智能导航等带来充足的信息量。截至目前，对三维点云数据的自动配准技术并不是十分完善，国内外诸多学者对该领域进行了各种尝试以及深入的研究[3-4]。在众多的算法中比较经典的算法是由BESL和MCKAY[5]于1992年提出的最近点迭代法(iterative closest point，ICP)，当给定初始位置与相对姿态接近时，该算法的配准效果较好[4]；彭真等[6]针对强噪声且密度不均匀的点云进行高效、高精度配准的问题，提出了一种基于关键点提取与优化ICP的点云配准算法；赵夫群[7]提出了将几何属性与k-d树改进的ICP算法相结合的配准方法。但大量实验证明，ICP算法在运算时间上存在较大缺陷，在处理大型的三维点云数据时显得十分吃力。之后三维正态分布转换(3D-normal distribution transform，3D-NDT)算法[8]被提出，其可应用于点云匹配以及相近性扫描数据处理的相关领域中[9]。3D-NDT算法在处理大数据量的三维数据过程中，具有的精度高、速度快等特点深受欢迎[9-10]。虽然相较于ICP算法，3D-NDT算法有了相当大的进步，但其同样需要提供前期配准估计。对于2种算法而言，3D-NDT算法较适合处理三维扫描设备所提供的数据[9]。未匹配的点云如果没有提供初始的匹配估计，最终的匹配误差较大。王庆闪等[11]通过将3D-NDT算法与ICP算法结合增加了配准的精度，但在运行时间方面有较大缺陷。赵凯等[12]提出一种新的区域生长聚类正态分布变换(normal distributions transform with region growing clustering，RGC-NDT)算法。本文提出的算法首先运用3D-Harris算法结合快速点特征直方图(fast point feature histograms，FPFH)计算配准初始值，然后用3D-NDT进行精准匹配。

1 点云的初始配准

点云的初始匹配即粗匹配是指在未获得用于配准的旋转变换矩阵的情况下，根据点云数据中含有的局部位置特征信息能唯一代表各自点云数据的性质，提取该点云的特征点，并根据FPFH原理计算每一个特征点处的特征描述子，进而求解用于将整个点云空间进行空间变换的特征向量以及旋转矩阵，完成点云最初始的点云粗匹配。图1为点云初始配准算法的流程图。

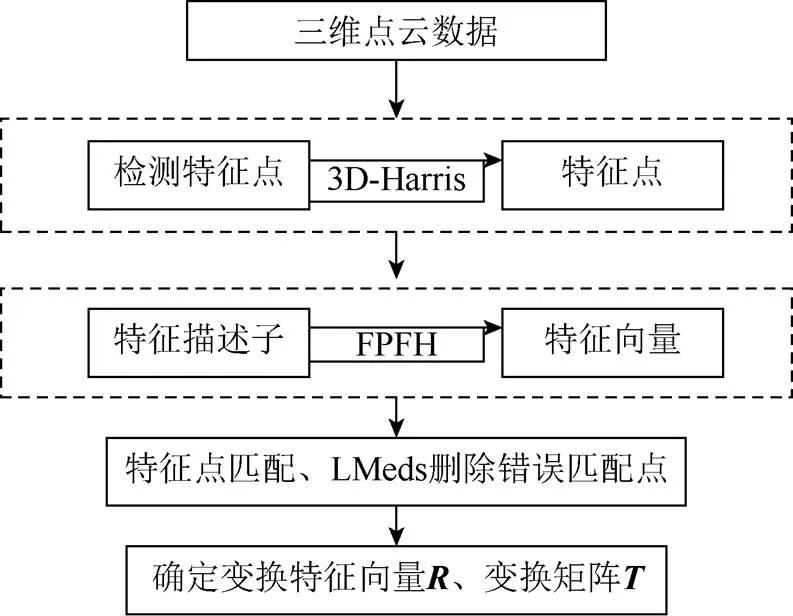
图1 初始匹配算法流程图

1.1 3D-Harris提取关键点

3D-Harris算法是针对1988年由HARRIS和STEPHENS[13]提出的Harris检测算法在三维方向的空间拓展。该算法需对整个点云空间进行三维网格化，将落在每个网格中点的个数近似看作二维图像的像素值，并以此为基础以前、后、左、右、上、下6个为平移方向进行计算，最终求得所有特征点。

1.1.1 Harris基本原理

将[,]平移[,]个单位后，其灰度的变化中(,)为平移后的强度；(,)为原图像强度。根据图像强度可以得到一个特征期望(,)如式(1)，当强度恒定时，(,)接近于0，反之，(,)会很大，即

其中，为一个5×5的窗口权函数。传统的函数将窗口内的各个权值设为1，其计算精度不高且易受噪声影响或利用高斯函数进行加权，每一次遍历都要重新计算高斯权函数，本文将窗口权值函数设置为梯度分段加权函数及将窗口从内到外分为5个等级，最中心的权为10，向外依次赋予权值7，5，3，1，如此改进Harris算法不仅提高了计算精度，也降低了计算复杂度。利用二维泰勒公式展开并取其一阶近似方程，可得简化式(2)

将计算的与设定的进行比较，当>即识别为特征点。

1.1.2 3D-Harris提取特征点

提取特征点是前期粗配准的关键一步，只有提取出一定数量的特征点，并根据其的FPFH特征信息才能计算出用于前期配准的变换矩阵。Harris最终要计算式(3)中的。但在三维点云空间领域中很难获取到如二维图像类似的图像强度，计算矩阵较为困难。

在整个三维点云空间中，以点为中心，以为半径来建立空间影响区域，在该区域内将所有的点进行主成分分析(principal component analysis，PCA)，利用最小二乘拟合出一个二次曲面，即

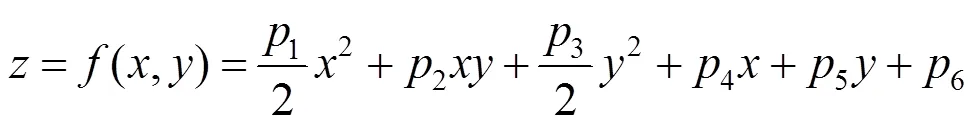
根据的计算公式，计算的和的偏导，近似成图像强度，并在该区域内利用曲面积分来解算出矩阵中的各个元素，如式(5)~(7)

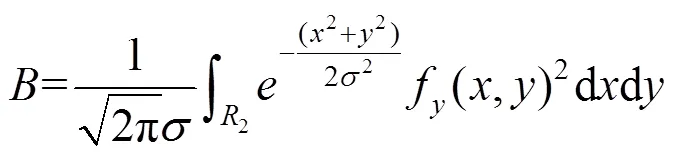
利用微积分知识可以计算得到，，的值，即

最后计算Harris响应值，进而判断关键点。

1.1.3 3D-Harris算法流程

(1) 体素化整个点云空间；

(2) 从体素开始，计算建立局部坐标系，方向为法向量方向，轴、轴与轴垂直，轴方向在平面内任意，轴在平面内与轴垂直；

(3) 根据体素内点云个数求解点云的梯度；

(4) 计算相关矩阵；

(6) 采取非极大值抑制对进行处理，将大于阈值的局部极大值点作为角点。

1.2 FPFH快速点特征直方图

FPFH[14]是对PFH[15]算法的改进，能快速地提取含有局部特征的描述子，并可以与关键点相结合。其具有较好的鲁棒性、时效性。表1中FPFH特征向量的维度为33，在较少维度的情况下反映特征信息，降低了算法的计算复杂度。

表1 各种特征描述子对应的特征向量的维度

算法流程：

(1) 迭代点云，计算法线；

(2) 点云中的每个点P，遍历P周围半径为的球体内的所有相邻点，将该点集合命名为P；

(3) 将P与其相邻的点进行关联。对于该区域中的一对点1和2，将法向量与1和2相连矢量夹角小的点设置为源点P，另一个点设置为目标点P；

(4) 计算3个特征(PFH的4个特征中除去P与P之间的距离，其表示目标点P处的平均曲率)，并组合放入存储单元中；

(5) 计算查询点P的简化特征直方图SPFH；

(6) 将相邻的SPFH之间的空间距离添加到P的SPFH中，构成FPFH。

1.3 LMeds删除错误对应

在获取了FPFH的特征向量之后，为了判断点云之间的重合部分，需要找到各点云之间的近似特征，进而完成点云初步的匹配工作。为了使匹配具有较高的精确性和准确度，采用了对应关系估计、求解各个点云数据之间的相互对应关系，最终得到其交集作为最后的相互关系匹配对。

由于数据在摄取过程中存在噪声的影响，3D-Harris算法会产生一些错误特征点，最终导致对应匹配关系也会出现错误的匹配，且对后续的求解变换矩阵造成很大的负面影响。所以，采用了最小中值法(least median of squares，LMeds)[16]删除错误对应关系，此操作不但能够节省配准所需的时间，同时也可以提高变换矩阵的计算准确度。

1.4 计算变换矩阵完成初始配准

使用LMeds算法删除了错误的点云对应关系，获得较高准确度的匹配点对进而完成了点云的初始配准后，获取了点云匹配的旋转矩阵和平移特征向量，即

如果点云和上分别有一个同名点，即关联点对(,,)和(,,)，则两者之间的数学关系如下

2 3D-NDT点云配准算法

2.1 3D-NDT算法原理

(1) 将点云空间划分为大小相等的单元要素(cell)，并将点云放入所有的体素之中；

(2) 计算每个cell的概率分布函数中的参数，即

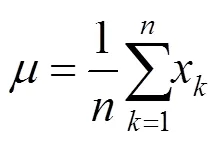
其中，为点云落在某个cell中的点的个数。

(3) 将下一幅的scan中的每一个点按照变换矩阵进行变换；

(4) 矩阵进行变换计算，相对应的概率分布函数如式(16)所示，将整个点云空间用一组正态分布函数{(,)}进行表示，最终形成一个分段式平滑空间函数，即

(5) 计算所有点的最优解，目标函数为

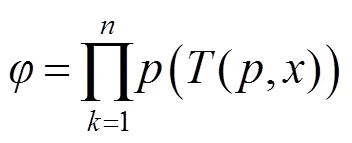
2.2 3D-NDT算法配准

首先建立一个4行4列矩阵用于存储变换矩阵。将3D-NDT的最初变换矩阵赋值给单位矩阵。在此基础上，进行3D-NDT算法匹配2点云。

考虑到算法运行的时间因素，将目标点云进行一定程度的缩减。对点云而言，3D-NDT算法使用整个体素化后的空间中的每一个单元格(cell)内的统计数据。此外，算法可以依据点云数据获取的大小来使用自适应参数的More-Thuente算法进行搜索，得到最理想的迭代步长，以防止出现过度迭代或局部收敛等问题。

同时，为最小的变换插值设置阈值，而且分别从长度和角度(以弧度形式表示) 2个方面定义每次变换的最小增量，当小于阈值时，即可结束本次匹配工作。

2.3 逐步点云匹配方法

该算法处理第3组多幅点云数据时，将点云逐一匹配，再将所有点云变换到同一个空间参考系下。以第1幅点云为基础，在点云重叠区域进行FPFH粗配准，进行3D-NDT精确配准得到最终的、最优的变换位置；最后将最优变换进行累积和不断更新得到整体的全局转换。再将所有点云按照读取顺序逐一变换到第1次输入的点云中，最终将所有点云匹配到与第1次读取点云相同的统一空间参考系下。本次实验证明，该方法实现的效果较好，可以较好地匹配多幅点云，最终实现场景复原，3D-Harris-FPFH-3D-NDT算法流程如下：

3 实验结果及分析

本次实验所用数据共3组，第1组数据是在csdn网站下载的由三维激光扫描仪获取1组室内扫描数据，如图2(a)和(b)所示；第2组为Kinect V2.0传感器获取的一个模型羊的点云数据如 图2(c)~(h)所示，该点云模型是重叠度较低的一组数据；第3组为采用Kinect V2.0传感器对实验室同一场景获取并进行Tatistical Outlier Removal滤波器滤波后的一组高重叠度点云数据，如图2(i)~(l)所示。具体实验数据参数见表3。随后在vs2013开发环境下结合PCL1.8.0点云开发资源库[17]完成实验。

表2 各点云滤波后点数量

如图3所示，对点云数据运用3D-Harris算法进行关键点检测。检测到的特征点个数见表3。如图3(a)~(h)所示，可以看出，3D-Harris算法所提取的关键点均位于变化较大的关键位置上，十分适合应用于这种室内场景。而且在相邻2幅的相同位置的关键点较多，说明3D-Harris算法是比较稳定的。

求解由3D-Harris算法所得到的特征点上的FPFH特征矩阵，在各个关键点处(设某一个特征点为0)将搜索半径设置为(本次实验=55 mm)。并且先遍历此区域内的所有点(1,2,···,)，再计

算0与各点对应法向量的夹角偏差{(1,1,1), (2,2,2),···,(,,)}。将所有的,,关键要素各自分化成11个子统计区间，计算特征直方图然后得到一组33维的特征向量。如图4所示，横坐标分成0~32个区域，纵坐标为落在每个分量上点的个数。由于关键点的数量较多，不能将每1幅点云中的全部特征点的FPFH特征矩阵全部显示出来，仅展示了1个点的描述子：

从图4可以得知，将局部特征用直方图表示之后，特征点相较于普通点而言差异量化的效果十分显著。

图5(a)~(i)分别显示了配准之前、及在循环次数相同情况下(本次迭代50次，此时对比效果最佳)，直接应用传统3D-NDT算法，将4幅点云进行配准和使用本文改进的算法所生成的效果图。具体细节对比如图6(a)~(f)所示，可以看出直接应用传统的3D-NDT算法在一定程度上对多幅点云的配准会起到一定的作用，但是误差较大；而本文方法可以在迭代次数较少情况下，将多幅点云较好地匹配到同一个坐标系下。

图3 各组数据的特征点分布示意图

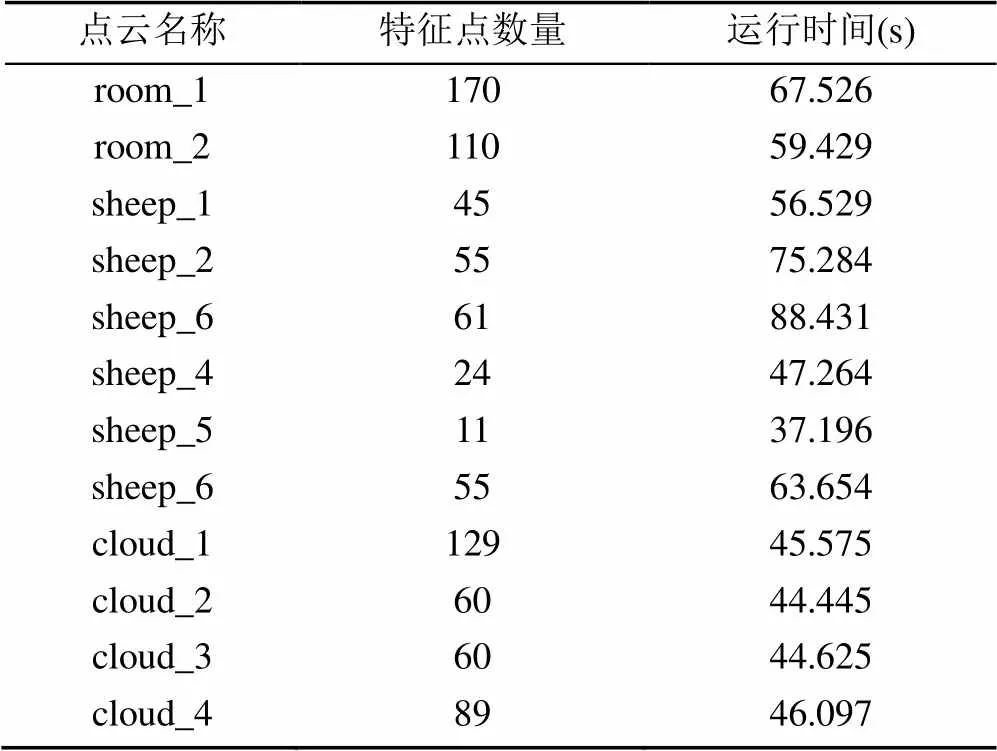
表3 各组点云数据的特征点数量

图4 FPFH特征直方图

为了进一步的检验本文所提出算法的精度以及准确性，本文还与其他一些常用的配准算法3D-NDT，ICP，SIFT-3D-NDT从计算精度和算法效率进行对比分析，见表4~6，结果证明当迭代次数相同时本文算法误差较小。

除上述所列的传统特征配准方法外，文献[18]还提出了一种新的特征提取配准方法，即基于协方差描述子的雷达点云配准算法，该算法的描述子为一个10为向量，且需包含点云的表面色彩纹理信息，而在本文数据中只有第3组数据含有表面纹理数据。且由于描述子只有10维特征向量，所描述的几何特征信息较少。如果将RGB信息全部设置为固定值，特征描述子只能近似为7维向量，不足以作为一个特征描述子来确定对应关系，会产生更多的错误对应关系。而在处理第3组数据时，由于Kinect生成的数据含有较多噪声，产生的对应匹配关系同样不理想，匹配精度不足，算法精度与传统的3D-NDT算法相近。该算法在处理专业的TLS扫描仪扫描获取的高精度彩色点云或许会有理想的效果，但对于本文的由Kinect所获取的室内点云数据的处理效果不佳。

图5 各组数据结果对比图

图6 各组数据结果细节对比

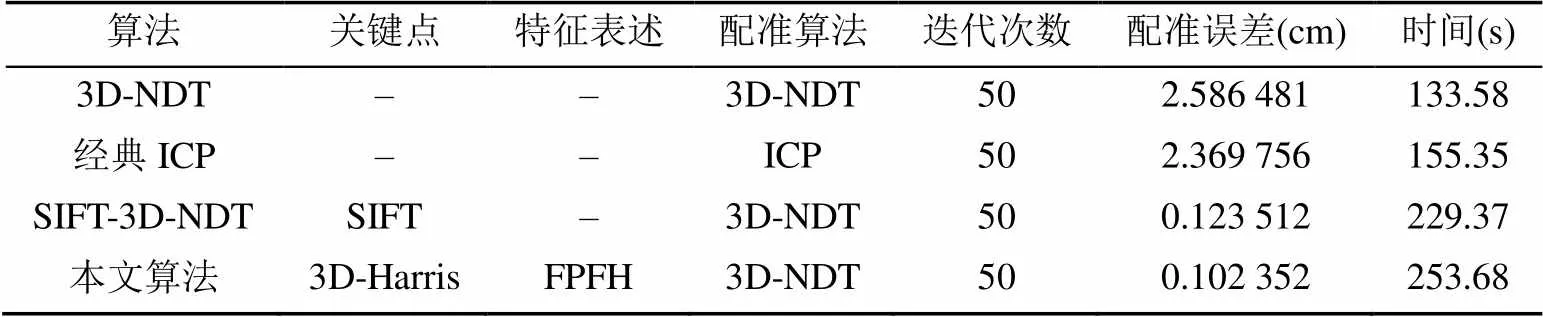
表4 第1组数据同类算法精度对比

表5 第2组数据同类算法精度对比

表6 第3组数据同类算法精度对比

通过实验可以看出，在配准前，各组点云均散乱堆叠在一起，在直接使用3D-NDT算法进行配准后，虽然在一定程度上完成配准，但误差较大，且容易受到噪声的影响，由于第2和3组数据含有很多噪声，所以该现象尤为突出。而改进的算法能很好地避免该问题。在对重叠度较低的点云进行配准方面本文算法也有一定优势。本文算法是基于3D-NDT算法改进而来，先为其提供一个初始值，与3D-NDT算法的敛散性相同，但收敛速度高。故具有很好的全局收敛性。表5~7通过与其他经典配准算法相对比，本文算法克服了无初始变换矩阵时配准误差较大的缺点，使精度得以提高。但由于算法的复杂度增加了，所以算法运行时间有所增加，需进一步解决。

4 结论与展望

本文针对Kinect V2.0传感器以及其他来源的室内三维点云数据的特征，有针对性地提出了3D-Harris-FPFH-3D-NDT点云配准算法，并将该算法与逐步配准算法相结合，将同一场景内的事物在不同位置，以不同角度拍摄的多幅点云数据进行逐步配准，最终，达到了预期要求。通过实验得到以下结论，在未得到配准所需的初始转换估计的情况下，本文算法可以在迭代次数较低时完成较为精确的多幅点云数据的自动配准。但由于算法增加了2个计算步骤，即3D-Harris、FPFH特征描述子的计算，提高了算法整体的复杂度。故该算法在如何降低计算复杂度，缩短运行时间方面需要进一步研究。

[1] 刘俊毅. 彩色图像引导的深度图像增强[D]. 杭州: 浙江大学, 2014. LIU J Y. Depth map enhancement under the guidance of color image[D]. Hangzhou: Zhejiang University, 2014 (in Chinese).

[2] 王欢, 汪同庆, 李阳. 利用Kinect深度信息的三维点云配准方法研究[J]. 计算机工程与应用, 2016, 52(12): 153-157. WANG H, WANG T Q, LI Y. Research of 3D point-cloud registration method based on depth information of Kinect[J]. Computer Engineering and Applications, 2016, 52(12): 153-157 (in Chinese).

[3] DU S Y, ZHENG N N, YING S H, et al. Affine iterative closest point algorithm for point set registration[J]. Pattern Recognition Letters, 2010, 31(9): 791-799.

[4] 刘鑫, 许华荣, 胡占义. 基于GPU和Kinect的快速物体重建[J]. 自动化学报, 2012, 38(8): 1288-1297. LIU X, XU H R, HU Z Y. GPU based fast 3D-bbject modeling with Kinect[J]. Acta Automatica Sinica, 2012, 38(8): 1288-1297 (in Chinese).

[5] BESL P J, MCKAY N D. A method for registration of 3-D shapes[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1992, 14(2): 239-256.

[6] 彭真, 吕远健, 渠超, 等. 基于关键点提取与优化迭代最近点的点云配准[J]. 激光与光电子学进展, 2020, 57(6): 68-79. PENG Z, LV Y J, QU C, et al. Accurate pair-wise registration of 3D point clouds based on key point extraction and improved iterative closest point algorithm[J]. Laser & Optoelectronics Progress, 2020, 57(6): 68-79 (in Chinese).

[7] 赵夫群. 基于改进ICP的点云配准算法[J]. 信息技术, 2017, 41(5): 64-66, 71. ZHAO F Q. Point cloud registration method based on geometric property and improved ICP[J]. Information Technology, 2019, 43(4): 33-38, 71 2020, 57(6): 68-79 (in Chinese).

[8] BIBER P, STRASSER W. The normal distributions transform: a new approach to laser scan matching[C]// Proceedings 2003 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS 2003). New York: IEEE Press, 2003: 2743-2748.

[9] KIM J W, LEE B H. Robust and fast 3-D scan registration using normal distributions transform with supervoxel segmentation[J]. Robotica, 2016, 34(7): 1630-1658.

[10] MAGNUSSON M, ANDREASSON H, NÜCHTER A, et al. Automatic appearance-based loop detection from three-dimensional laser data using the normal distributions transform[J]. Journal of Field Robotics, 2009, 26(11-12): 892-914.

[11] 王庆闪, 张军, 刘元盛, 等. 基于NDT与ICP结合的点云配准算法[J]. 计算机工程与应用, 2020, 56(7): 88-95. WANG Q S, ZHANG J, LIU Y S, et al. Point cloud registration algorithm based on combination of NDT and ICP[J]. Computer Engineering and Applications, 2020, 56(7): 88-95 (in Chinese).

[12] 赵凯, 朱愿, 王任栋. 基于改进NDT算法的城市场景三维点云配准[J]. 军事交通学院学报, 2019, 21(3): 80-84. ZHAO K, ZHU Y, WANG R D. Urban scene 3D point cloud registration based on impove NDT algorithm[J]. Journal of Military Transportation University, 2019, 21(3): 80-84 (in Chinese).

[13] HARRIS C, STEPHENS M. A combined corner and edge detector[C]//Procedings of the Alvey Vision Conference.Heidelberg: Springer, 1988: 147-151.

[14] RUSU R B, BLODOW N, BEETZ M. Fast point feature histograms (FPFH) for 3D registration[C]//2009 IEEE International Conference on Robotics and Automation. New York: IEEE Press, 2009: 3212-3217.

[15] RUSU R B. Semantic 3D object maps for everyday manipulation in human living environments[J]. KI - Künstliche Intelligenz, 2010, 24(4): 345-348.

[16] 李春磊, 常智勇, 莫蓉. 基于改进LMedS算法和贪心估计的相位立体匹配[J]. 计算机辅助设计与图形学学报, 2014, 26(11): 2046-2055. LI C L, CHANG Z Y, MO R. Phase-based stereo matching by using improved LMedS algorithm and greedy strategy[J]. Journal of Computer-Aided Design & Computer Graphics, 2014, 26(11): 2046-2055 (in Chinese).

[17] 朱德海, 郭浩, 苏伟. 点云库PCL学习教程[M]. 北京: 北京航空航天出版社, 2012: 1-402. ZHU D H, GUO J, SU W. Point cloud library PCL. Beijing: Beihang University Press, 2012: 1-402 (in Chinese).

[18] LI W, WANG C H, WEN C L, et al. Pairwise registration of TLS point clouds by deep multi-scale local features[C]//Neurocomputing, 2019 Nicolas Bonneel and David Coeurjolly. New York: ACM Press, 2019: 13.

Improved 3D-NDT point cloud registration algorithm based on 3D-Harris and FPFH

FAN Qiang1, LIU Peng1, YANG Jun2, ZHOU Pei-xi1

(1. School of Geomatics, Liaoning Technical University, Fuxin Liaoning 123000, China; 2. School of Urban and Environmental Sciences, Liaoning Normal University, Dalian Liaoning 116029, China)

Aimed at addressing the shortcomings of the traditional point cloud registration normal distribution transform (3D-NDT) and iterative closure points (ICP) algorithms, such as poor registration effect, long registration time and serious errors, a precise and relatively efficient point cloud matching algorithm was proposed. First, the 3D-Harris algorithm was used to identify the key points of each point cloud, and the key points were adopted to establish a local reference frame for the basic points and calculate the fast point feature histograms (fpfh) descriptor. Then, the corresponding estimation algorithm of the least median of squares (LMeds) minimum median method was utilized to eliminate the inaccurate point correspondence and obtain the feature point pairs with corresponding 3D feature relationships. The transformation matrix required for coarse registration was calculated to complete the preliminary registration. Subsequently, according to the 3D-NDT algorithm, the point cloud data space was voxelized, and the probability distribution function was employed to complete the final point cloud for accurate registration. Finally, we used this method to match three groups of point cloud files, which were downloaded from the network with less noise and large-scale overlapped with more noise collected by Kinect V2.0 to the same spatial reference frame, and compared the classical 3D-NDT, ICP and other algorithms through accuracy analysis. The experimental results show that the proposed algorithm can achieve the high accuracy registration of point cloud data in indoor scenes with low iteration times and is less affected by noise. However, how to reduce the complexity of the algorithm appropriately and shorten the registration time needs further research.

3D normal distributions transform; 3D-Harris key points; fast point feature histograms; least median of squares; point cloud registration

TP 391

10.11996/JG.j.2095-302X.2020040567

A

2095-302X(2020)04-0567-09

2020-02-20；

2020-04-28

28 April，2020

20 February，2020；

国家自然科学基金项目(41771178)

National Natural Science Foundation of China (41771178)

范 强(1979-)，男，辽宁锦州人，副教授，博士。主要研究方向为遥感信息提取与专题地图信息系统。E-mail：120853030@qq.com

FAN Qiang (1979-), male, associate professor, Ph.D. His main research interests cover remote sensing information extraction and thematic map information system. E-mail：120853030@qq.com