基于机器视觉光流法的涡旋可视化及测量①

李飞，邱文扬，郭志帮，李天乐，邓锂强

(广东石油化工学院 理学院，广东 茂名 525000)

涡旋是自然界普遍存在的一种流动现象，广泛存在于工程设计、军事探测、气候预测等，因此对涡旋产生的研究及测量具有重要意义。中国海洋大学海洋与大气学院物理海洋教育部重点实验室使用旋转平台[1]的方法产生涡旋，这样产生的涡旋是一个定常的涡旋，只在垂直方向发生变化，并不能在水平方向移动。而自然情况下，涡旋既可水平方向移动，也可竖直方向移动，其本质为涡旋能量的耗散。流体力学表明，流体中只要有涡量源存在，就会产生涡。本实验紧抓涡旋产生的性质，采取“搓”的形式产生涡旋，使用舵机做成一个类似机械臂加上一个船桨，以划船的形式滑动水体。由于流体一层一层之间有体积力(引力、惯性力、电磁力、柯氏力)、表面力的作用，最终形成可观的流线，在一定程度上形成客观的涡旋。目前，测量涡旋的主要方法为PIV方法，但PIV系统成本较高且受空间分辨率限制。随着机器视觉图像算法的广泛应用，光流法主要应用于目标检测和目标跟踪，早期的光流法采用了Lucas-Kanade 方法[2]，2002年Farneback基于图像恒定假设提出了Farneback光流法[3]，与Lucas-Kanade 方法相比，其准确率更高。该方法为稠密光流法，可以计算每个点的运动速度。基于此，本文将该方法推广到流体涡旋的测量。

1 实验装置与测量方法

1.1 实验装置

实验装置如图1所示，位于下方的水槽为亚克力板材质，100.0 cm×60.0 cm×25.0 cm(长×宽×高)，水槽壁厚0.5 cm，水槽底部为纯白色。实验时水槽注水深15 cm(水的深度对涡旋有一定影响，但本实验重点在于使用光流法测量涡旋，探索光流法测量涡旋的可行性)，待液面平稳，将舵机控制器连接到计算机，使用计算机的舵机控制软件，设定舵机的动作(主要有舵机的转动角度、转动速度、桨的入水深度、倾斜角度)。启动电源后，摄像头下面将会形成涡旋并向一个方向移动。本实验采用的摄像头像素为100万，视频采集帧数为30 帧/s，摄像头在B调节支架上可以调节高度，从而调整视频采集区域。

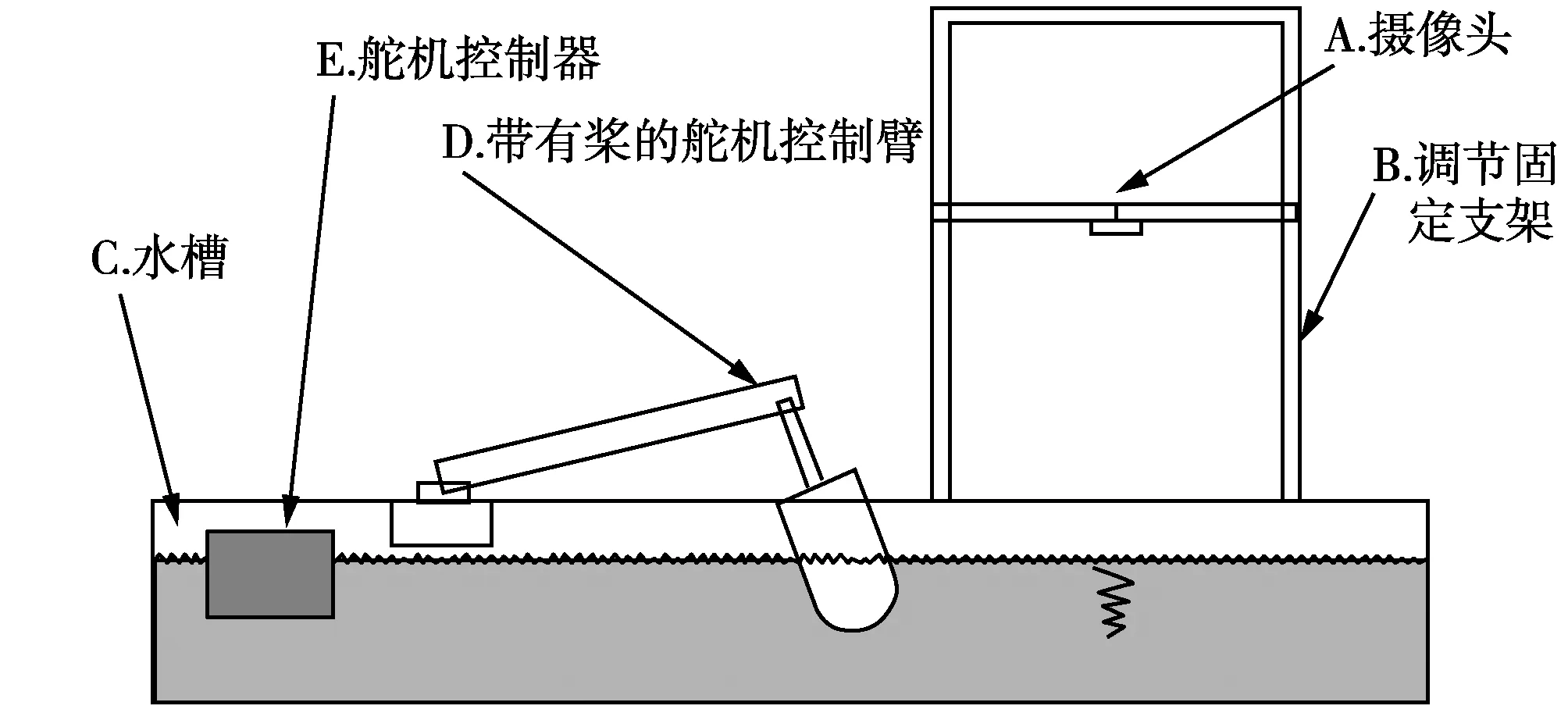
图1 实验装置

1.2 机器视觉光流法原理

光流场就是用于描述三维空间中的运动物体表现到二维图像中的一种方法，所反映的是像素点的运动向量场。光流法利用图像序列中的像素在时间域上的变化、两帧之间的相关性来计算出两帧之间物体的运动信息。光流法作出如下假设[4]：(1)同一个空间像素灰度值，在各个图像固定不变；(2)相邻帧像素运动较小；(3)邻域具有相同光流。假设图像序列可表示为

I(X,t)，X=[x,y]

(1)

式中：I为像素点光流亮度强度；X为流场位置。

视频中的每个前后帧提取出来之后可作为一个图像序列。假设图像亮度恒定，即图像亮度没有变化，则导数为0。根据泰勒展开可得

(2)

(3)

在微小时间内的速度，可以记为

(4)

则有：

(5)

得到的方程为光流方程，亦为超定方程。光流法核心是要求解此方程，得到u，v值。求解此方程需要用到Farneback算法。Farneback假设图像梯度和局部光流不变。从摄像头获得的二维图像可表示为

I(X)=XTAX+bTX+c

(6)

对式(6)进行系数化则：

I(x,y)=r1+r2x+r3y+r4x2+r5y2+r6xy

(7)

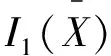
=XTAX+(b-2Ad)TX+dTAd-bTd+c

(8)

据光流法基本假设，有：

A1=A，b1=b-2Ad，c1=dTAd-bTd+c

(9)

如果A1非奇异，则由式(9)可得

(10)

理论上有A1=A，但实际中难以能满足这一项要求，因此需要通过求平均值来近似真实值。所作处理如下：

(11)

用空间变化的位移场来替代全局变量d，得到

A′(X)d(X)=Δb(X)

(12)

理论上，式(12)可以逐点求解，但是这样不利于提高算法的稳定性也会对计算成本造成浪费，这时需要对邻域进行估计。假设位移场只是缓慢变化的，就可以在每个像素的邻域上集成信息，因此需要尽可能地在邻域中找到最小化领域范围。

(13)

根据二维高斯分布确定的邻域中每个点的权函数，利用最小二乘法的原理可得：

d(X)=∑(ωATA)-1∑ωATΔb

(14)

这意味着要先计算ATA和ATΔb，再通过权重函数ω进行加权平均运算，最终根据式(14)求解位移，此解决方案存在并且是唯一的。当位移场可以根据某种运动模型进行参数化时，就可以提高算法的鲁棒性。对于线性参数运动模型来说，一个具有六个参数的运动模型为

工笔画花鸟题材。工笔花鸟也是现代皮雕工艺表现的一个方面。从走刀线到压边，起鼓，打阴影，再上色，通过这样程序来表现传统工笔花鸟的意蕴。这类的皮雕风格，对刀线的要求较高，就和工笔画里的线条一样，起落有节奏，有轻重。没有太多的装饰线条，背景纹的处理也是结合中国工笔画特有的特点，有实有虚。并且结合工笔画晕染技法，用皮雕专用染料进行上色晕染，仿佛半立体的工笔画。

dx(x,y)=a1+a2x+a3y+a4x2+a6xy，dy(x,y)=a1+a2x+a3y+a5y2+a6xy

(15)

此时

D=SP

(16)

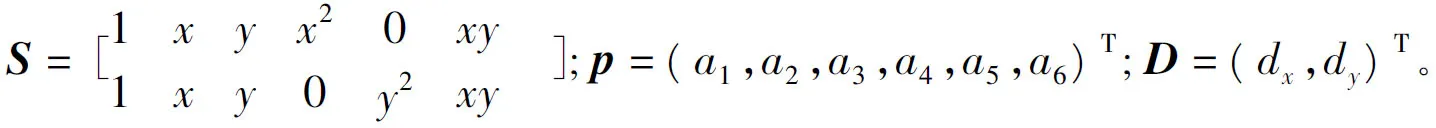
式(16)代入式(13)得到加权最小二乘法问题为

(17)

式中：i为邻域内各点像素的索引。

此时，式(17)的解为

(18)

通过计算STATAS和STATΔb，再对它们进行加权平均，最终计算得到位移。

由于光流法的三个基本假设都是强假设，要求场景本身变化小，像素帧间运动足够小，但实际场景很难满足。尤其假设(3)，只适合变量较小的情况。因此，该算法还要引进金字塔算法。

1.3 金字塔算法

金字塔算法[5]有效地解决了像素位移较大的问题，其核心是缩小图片尺寸，缩小像素位移，图像足够小时，相邻两帧之间图像的大尺度运动将会被缩小，这样便适用光流法约束条件。该算法设定I、L相邻两时刻的图像，Ik、Lk为Ik-1、Lk-1层通过粗采样得到的较低分辨率的图像，这里用Ik、Lk层得到的最初估计光流场gL对L层作预平移Ik-1、Lk-1层在gL的基础上求该层的光流dL，这样求得的残余光流向量dL=[dLx，dLy]T就足够小，因此可以经过标准的光流法来求出这个运动矢量。再利用获得的dL与gL，对L-1层的g(L-1)做估计。最终所有层的分段光流d叠加得到光流和。使用金字塔图像计算光流，对一个大的像素偏移的矢量d，可以经过计算几个较小的残余光流来得到。

计算光流场使用Python-opencv库提供的Farneback光流法方案，该方法采用文献[6]基于Gunner Farneback提出的方法，可以得到整个流场中每个像素点的位移值。

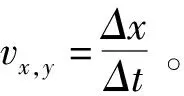
图2 摄像头与运动场

1.4 数据采集与处理

调整好装置可得到图3所示视场，调整舵机转速和桨的角度，使其在产生稳定的涡旋之后回到初始位置，并在涡旋产生时开始采集数据。光流算法计算每一个像素点的运动情况，实际使用python实时采集并处理计算量太大。数据采集先按摄像头可视范围和实际流场的边界对应，摄像头采集到尺寸为1280×720的视频，将其中270×75个像素点的数据导出到Excel。简要的算法流程见图4。

图3 流场可视化范围 图4 算法流程

得到数据后，用Matlab处理数据。对数据进行分析，发现有部分异常数据后，剔除异常值。使用拉依达法剔除异常数据，当测量值与平均值相差大于标准偏差的3.5倍时，将之剔除。此方法适合大样本数据，数据剔除效果见图5。

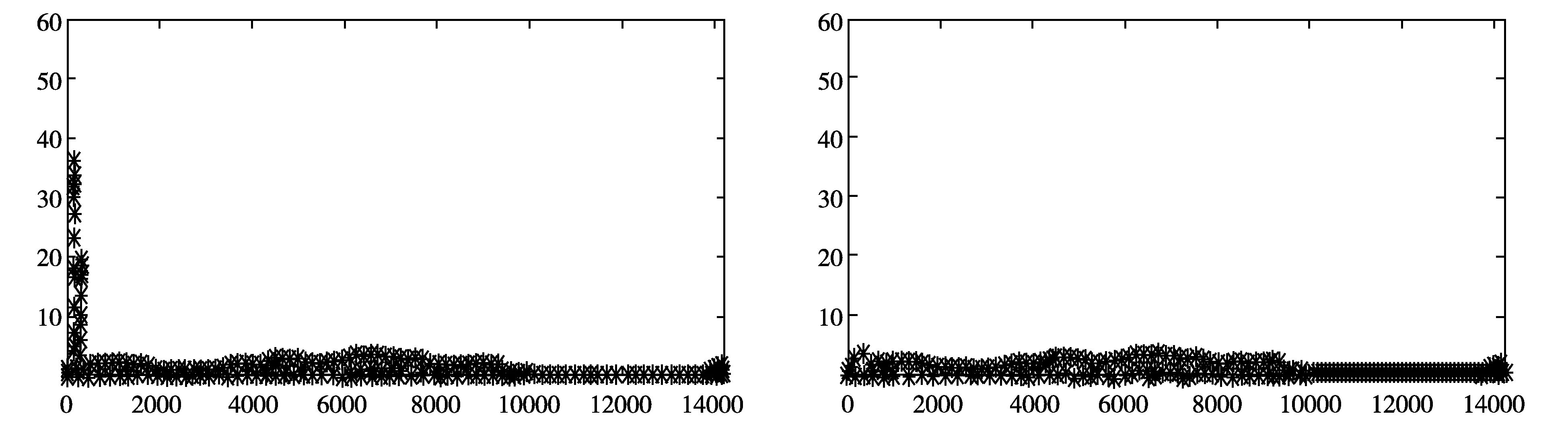
a 原始数据 b 剔除异常值后数据

(19)

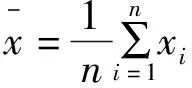
2 结果及分析

由速度环量和涡通量的斯托克斯公式，可以计算涡量，其表示为

(20)

式中：L，S分别为无线小圆的周长和面积。

去除高阶小量，平均切向速度为

(21)

式中：a为半径。

M点涡量的大小是流体微团绕该点旋转的平均角速度的两倍，方向与微团的瞬时转动轴线重合。其涡量表示为

(22)

实验中，相邻两帧之间由于时间极短，相邻两帧之间同一个点的位置的位移偏转角度可以看作这个点绕无限小的圈转动(见图6)。d1为第K帧某个位置的一点绕无限小圈转动，d2为第K+1帧同一个点绕同一个无限小圈转动，相邻两帧的角度通过光流法采集。

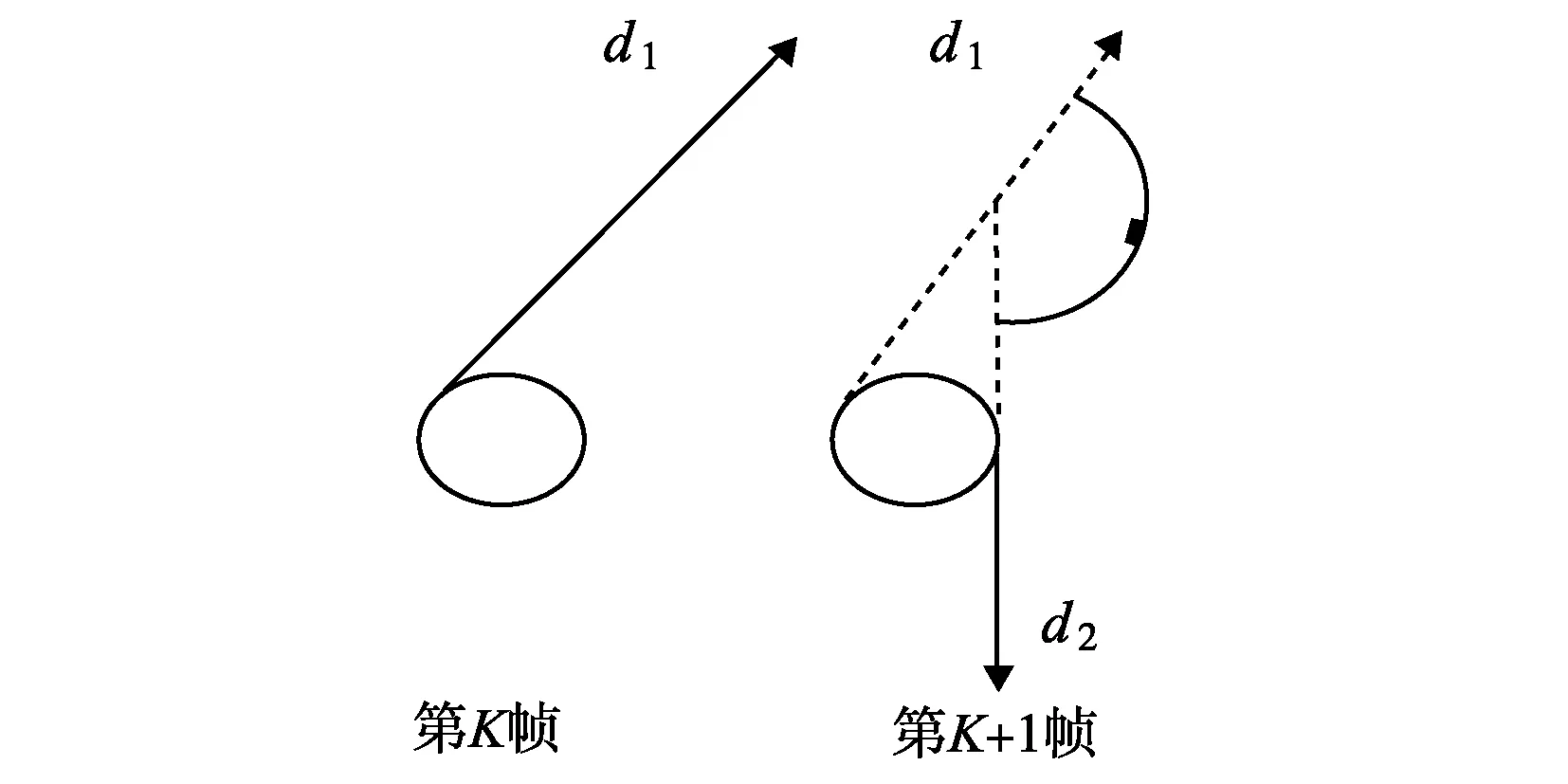
图6 相邻两帧流体微团偏转角度

通过光流法采集的数据，经过处理后得出流场的速度分布(见图7)和流场涡量分布(见图8)。

图7 流场速度分布 图8 流场涡量分布

由图7可知，涡旋产生时的速度很快，但涡旋移动速度耗散也很快。由图8可知，流场几乎处处都存在涡量，只有漩涡所在的位置涡量较小，甚至没有，这符合自由涡的理论。这证明了使用光流法可以对涡旋进行测量，其准确性在一定程度上接近理论值。

3 结语

本次实验将机器视觉光流法用于流体涡旋的测量，实验证明该方法在二维层面测量流场的速度分布等流体力学量是可行性的，同样使用光流法对海洋大气流场进行测量分析也许可行。但本实验没有使用海洋大气流场进行测量分析，这是该实验的不足之处。另外，光流法适用于二维层面，现实的流场是复杂三维的，所以光流法对三维流场具有一定的局限性，有待进一步探索。