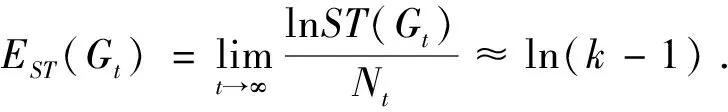一类k-正则图的生成树数目与熵

贾环身，吴廷增

(青海民族大学 数学与统计学院，西宁 810007)

生成树是反映复杂网络可靠性的一个重要物理指标，网络中生成树越多，则网络越健壮[1-5].对于一个连通网络，在保持节点数不变的情况下，其生成树具有最好的同步能力.熵是从信息论中借用的一个术语.它是对“信息量”或信息传递的“不确定”的度量.图的熵，是对有无图结构的一种测量.信息的基本单位是比特.因此, 熵是图中“随机性”的比特数；熵越高，网络的随机性就越高[6-10].文献[11]中，给出了一类4-正则图生成树的计算算法，本文推广了该结果，给出了k-正则图的生成树数目和熵.为了证明该结果，先给出一些定义和引理.

图G[12]是指一个有序三元组(V(G),E(G),ΨG)，其中V(G)表示顶点集，E(G)表示边集，ψG是关联函数.若e是一条边，而u和v是使得ψG(e)=uv的顶点，则称e连接u和v；顶点u和v称为e的端点.图G的顶点v的度dG(v)是指G中与v关联的边的数目.若各顶点的度均相同的无向简单图称为正则图.各顶点度均为k的正则图称为k-正则图.若图存在其中1个点的度数为(k-1)，分别只与其他(k-1)个点相连，称这样的图为k个顶点的星图Sk.不包含圈的图称为无圈图，连通的无圈图称为树.图G的一个生成子图T如果是树，则称它为G的一棵生成树，生成树T是一个连通图G的一个极小连通子图，包含G的所有n个顶点，有(n-1)条边的连通图.若T为森林，则称它为G的一个生成森林.为了方便，图G中生成树的个数记为NST(Gt).

引理1[3](Cayley公式)若e是Gt的边，则NST(Gt)=NST(Gt-e)+NST(gt·e).

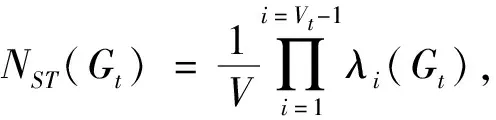
下面使用迭代法构造一类k-正则图.具体构造步骤如下：

1)当t=0时给出一个星Sk-1，记为F0，使得F0为一个k个节点连接k-1条边的k-1叉树；

2)当t=1时，取F0的一个拷贝并一一对应粘贴叶子节点，使得最底层的每个叶子节点的度为k，记为F1；

3)当t≥2时，在(t-1)步生成的(k-1)叉树Ft-1的每个叶子节点再生出(k-1)个叶子节点并复制Ft-1，粘贴两个Ft-1的最底层叶子节点使得它们的度为k，记为Ft(t≥2)(如图1).

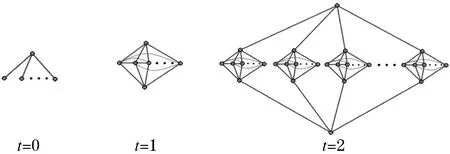
图1 Ft(t=0、1、2)的前三步迭代构造

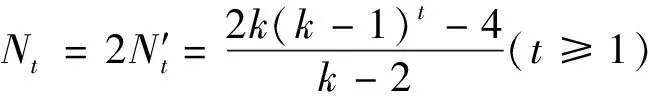
图2 Gt(t=0、1、2)的前三步迭代构造

直径指网络中所有节点对之间最小距离的最大值,它反映网络最大最大传递延迟的属性.小的直径与小世界网络的概念是一致的,这里用直径代替平均路径长度来说明网络的小世界特性.D(t)用表示本网络模型的时间步t时的直径.网络的直径为：D(t)=2t+1

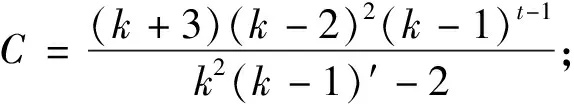
观察Gt, 不难发现Ft和Gt的关系，见图3.假设ST(Ft)表示在Ft中第t步时的生成树数目，SF(Ft)表示在Ft中第t步时具有两个分支的生成森林数目，那么通过计算Ft的生成树数目来求得原模型Gt的生成树数目.

定理1 设Gt为k-正则图(k≥3)，则

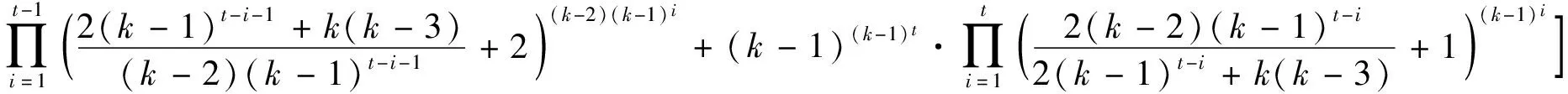
证明：由图3～5可得出，Ft在第t步时的生成树数目是通过迭代的方法由(t-1)步得到，并且t步的生成树是由(t-1)步生成树和生成森林共同构成，Ft有以下几种情形：

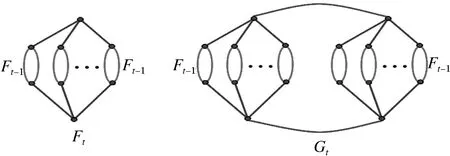
图3 t步时的网络Ft和Gt

ST(Gt)=2ST2(Ft)+2ST(Ft)·SF(Ft)

(1)

(2)

其中：ST(F0)=1,SF(F0)=k-1

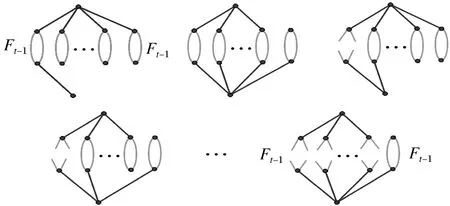
图4 每一类Ft的生成树

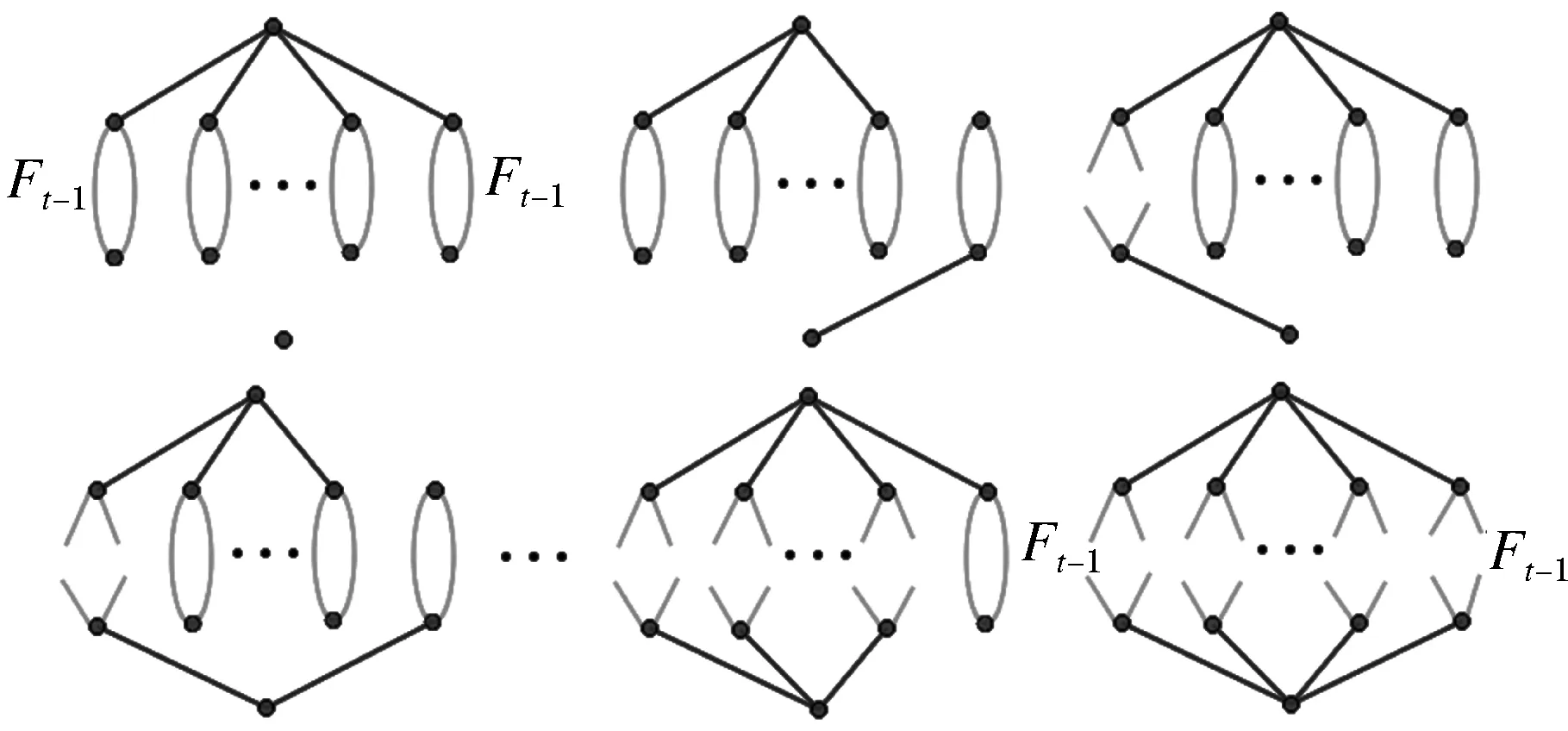
图5 每一类Ft中具有两个分支的生成森林

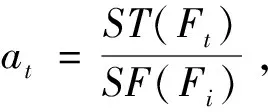
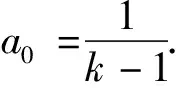
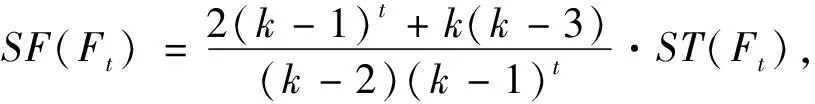
(3)

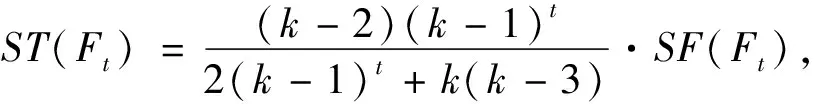
SF(Ft)=(k-1)(k-1)t·

(4)

根据式(3),(4)可推出公式(1)得到Gt的生成树数目，即：

由生成树数目，则的生成树的熵为：