高分子链在分子刷表面吸附的Monte Carlo 模拟*
2020-08-29王超周艳丽吴凡陈英才
王超 周艳丽 吴凡 陈英才
(台州学院物理系, 台州 318000)
1 引 言
高分子链在固液界面上的吸附一直是物理、化学和生物领域的热门课题, 其不仅与许多化工技术相关而且在生物系统中也广泛存在, 如: 高分子纳米粒子复合材料制备、材料表面改性和润滑、胶体稳定、DNA 在病毒内的封装等[1−9]. 因此, 深入研究高分子链吸附的静态和动态行为并揭示相应的物理机理, 对化工技术和生物医学技术的研究有重要意义.
高分子链在界面上的吸附受链的拓扑结构[10−13]、链的组成和柔性[14−16]、界面的几何形状[17,18]、外加作用[19−21]等众多因素影响. 对于均质界面的情形,高分子链与界面之间的吸引作用能(e)是一个重要的调控参数. 研究表明, 当吸引作用能超过临界值(eC)时, 高分子链会发生由脱吸附态到吸附态的相转变. 相应地, 高分子链构型由无规线团状转变为薄饼状[22]. Luo[23]曾根据二级相变有限尺寸标度理论得到了高分子链吸附链节数M(序参量)随链长N 以及吸引作用能e 的标度关系, 同时发现利用该标度关系可以很好地解释Monte Carlo 模拟结果并由此确定了eC. 这也意味着高分子链在平面附近的吸附相转变为二级相变. 另外, 高分子链的动态行为(如: 吸附时间、扩散和弛豫)也与界面吸引作用能有关[24].
除吸引作用能之外, 界面的细节结构也会对高分子链吸附产生重要影响. Cerda 和Sintes[25]曾考虑吸引条纹和中性条纹周期分布的界面, 发现高分子链的吸附存在两个临界吸附点(临界温度)和三种不同的吸附态. 进一步的研究表明, 高分子链在三种吸附态满足不同的扩散规律[26]. 对于吸附点在界面上随机分布的情形, Yang 等[27]发现高分子链的吸附时间随吸附点密度的增大而增大, 但在高密度和低密度区域满足不同的吸附机制, 同时还发现高分子链尺寸有可能随吸附点密度的增大而减小, 这与高分子链在均匀界面的吸附不同.
Milchev 等[28]最近考虑更为复杂的界面—分子刷界面, 发现随着自由高分子链与分子刷之间吸引作用的增强, 自由高分子链也会发生脱吸附到吸附的相转变. 但与固体界面不同的是, 根据分子刷密度和吸引强度不同, 自由高分子链在吸附态既有可能嵌入分子刷内部也有可能只吸附于分子刷表层. 这也意味着, 高分子链在分子刷上吸附的动力学过程可能比固液界面情形更为复杂, 然而目前关于这方面的研究还很有限. 受此启发, 本文用Monte Carlo 方法模拟研究了一条自由高分子链在分子刷界面上的吸附, 不仅考察自由高分子链由脱吸附态到吸附态的转变和链节空间分布变化, 还研究了自由高分子链的平衡态扩散过程和吸附动态过程, 发现自由链在脱吸附态和吸附态满足不同的扩散规律, 同时还发现整个吸附动态过程可分为自由链吸附和分子刷扩散两个阶段.
2 模型与模拟方法
整个模型系统建立在三维简立方格子空间(格子常数为长度单位), 如图1 所示. 单条长度为Nf的自由高分子链处在分子刷表面附近. 分子刷由nb条长度为Nb的端点吸附链(接枝链)组成.接枝链固定端均匀地分布在下界面(z = 0 位置)的格点上, 近邻固定端间的距离为d. 分子刷疏密程度取决于d, 即d 越小, 分子刷越密集, 反之,分子刷越稀疏. 另外, 为了防止自由链远离分子刷,假定在z = D 位置还存在一个纯排斥上界面, 即自由链限制在分子刷和上界面之间. 系统在x, y 方向上采用周期性边界条件.
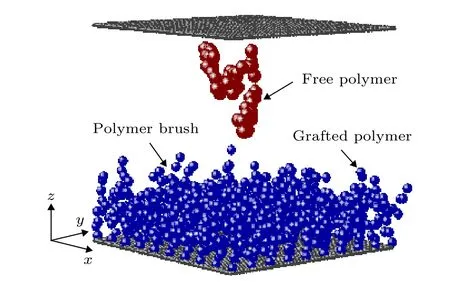
图1 模型示意图Fig. 1. A sketch of the simulation system.
自由链和接枝链均采用八格点键长涨落模型[29],具体地, 每个链节占据一个立方体的八个格点, 键连链节间的距离可以有五种取值(高分子链取这些键长可以自动避免键交叉的情况). 自由链链节之间、分子刷链节之间、自由链与分子刷之间、链节与界面之间均满足排除体积作用, 即空间任一格点都不能同时被两个或多个链节占据, 也不能同时被链节和界面占据. 除此之外,还假定当自由高分子链节中心与分子刷链节中心之间距离为2 (最近距离)时, 自由链与分子刷之间存在吸附作用能 e.
模拟开始时, 先在下界面上生成分子刷, 然后在分子刷和上界面之间生成自由高分子链. 系统生成后, 先设定自由链与分子刷之间吸附作用能为零(e = 0), 并让系统经过长时间的弛豫达到平衡态; 然后开启自由链与分子刷之间的吸附作用, 模拟并考察自由链的吸附和运动. 在模拟中, 分子链的运动通过单链节尝试运动实现. 链节尝试运动采用Monte Carlo 重要性抽样算法, 具体如下: 随机选择自由链或分子刷(除吸附端点外)上一个链节并使其随机地向近邻格点移动一个单位长度, 若链节新位置满足模型条件(如: 排除体积条件和键长条件), 则新位置被接收的概率为 min(1,e−∆E/kT) ,其中DE 为链节位置移动所引起的能量增量. 定义一个Monte Carlo 步长(Monte Carlo step, MCS)为Monte Carlo 模拟的时间单位. 在一个时间单位内共有 Nf+nbNb次链节尝试运动.
为了使自由链能尽快与分子刷接触, 选择分子刷表面到上界面之间的距离略大于自由链的自由回转半径Rg0(Rg0为自由链在自由空间的回转半径). 在模拟中固定分子刷接枝链总条数nb= 100,主要考察分子刷链长度Nb、间距d 以及吸附作用能e 对自由链的吸附、构型和运动的影响.
3 模拟结果讨论
首先研究了自由链吸附链节数mad(即与分子刷接触的自由链链节数)随吸附作用能e 的变化,如图2 所示. 可以看出, mad随e 的变化存在三个不同的区域: 1)当e 比较小时, mad→ 0, 即自由链处于脱吸附态; 2)当e 比较大时, 自由链处于吸附态, mad趋于饱和值mads; 3)当e 取中等值时,mad随e 的变化存在一个明显的转变区, 在该区域mad由0 快速增大为mads. 在吸附态, 自由链可能同时与多条接枝链相吸附, 因此自由链上必然有部分链节介于不同接枝链之间而不被吸附, 称之为桥链节. 随着d 的增大, 桥链节数目将不断增大, 从而导致mads不断减小, 如图2 所示. mads还与接枝链长度Nb有关. 随着Nb增大, 自由链周围分子刷链节不断增多, 这将使得自由链被吸附链节数mads不断增大(结果未给出). 为了描述mad随e 变化图中转变区的位置, 定义比值mad/mads=0.5 对应的e 为临界吸附能eC, 如图2 插图所示.可以看出, 临界吸附能eC几乎与自由链长度Nf无关, 但随接枝链间距d 的增大而增大. 同时可以发现eC随接枝链长度Nb的增大而减小(结果未给出). 随着d 增大或Nb减小, 自由链周围分子刷链节不断减少, 因此需要更强的吸附作用才能使自由链吸附在分子刷上, 从而导致eC不断增大, 这与链滴理论(the blob theory)得到的结果定性一致[28].Luo[23]的研究表明, 高分子链在吸附平面附近的相转变属于二级相变. 虽然分子刷界面与吸附平面在微观结构上有很大不同, 但高分子链在两种界面附近由脱吸附到吸附的宏观转变却非常相似. 因此,我们认为高分子链在分子刷表面附近的脱吸附-吸附相变类型也为二级相变.
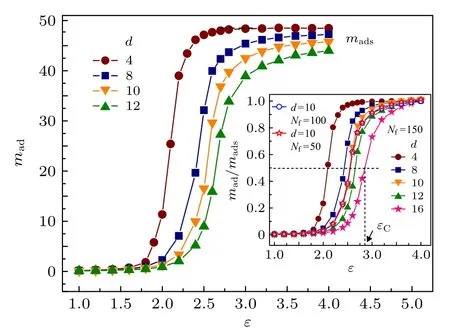
图2 d 取不同值时, 自由链 吸附 链节数mad 随吸引作用能e 的变化, 其中Nf = 50, Nb = 10. 插图: Nf 和d 不同时,比值mad/mads 随e 的变化Fig. 2. The number of the adsorbed segment of the free polymer mad as a function of the adsorption energy e for different d, where Nf = 50 and Nb = 10. The inset presents the dependence of the ratio mad/mads on e for different Nf and d.
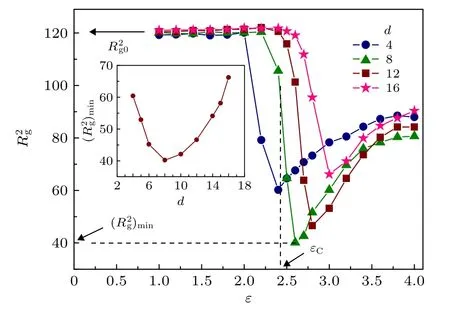
图3 d 取不同值时, 自由链均方回转半径 R2g 随e 的变化,其 中Nf = 50, Nb = 10. 插 图: R2g的最小值 (R2g)min 随d 的变化Fig. 3. The mean square radius of the free polymer R2g as a function of e, where Nf = 50 and Nb = 10. The inset presents the dependence of the minimum of R2g , (R2g)min ,on d.
为了理解自由链尺寸的变化, 分别研究了e
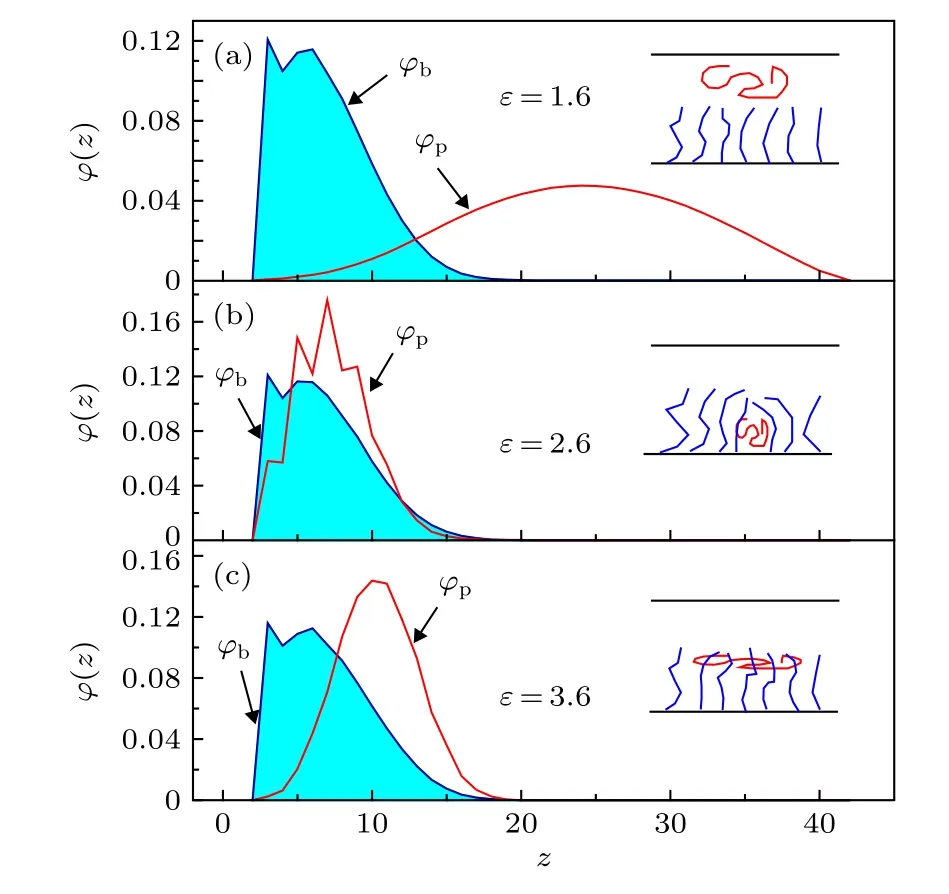
图4 e 取不同值时, 自由链及分子刷链节在z 方向上的分布jp 和jb, 其中Nf = 50, Nb = 10, d = 12Fig. 4. The distribution of the segment of the free polymer and the polymer brush, jpandjb, in the z direction for three different e, where Nf = 50, Nb = 10 and d = 12.
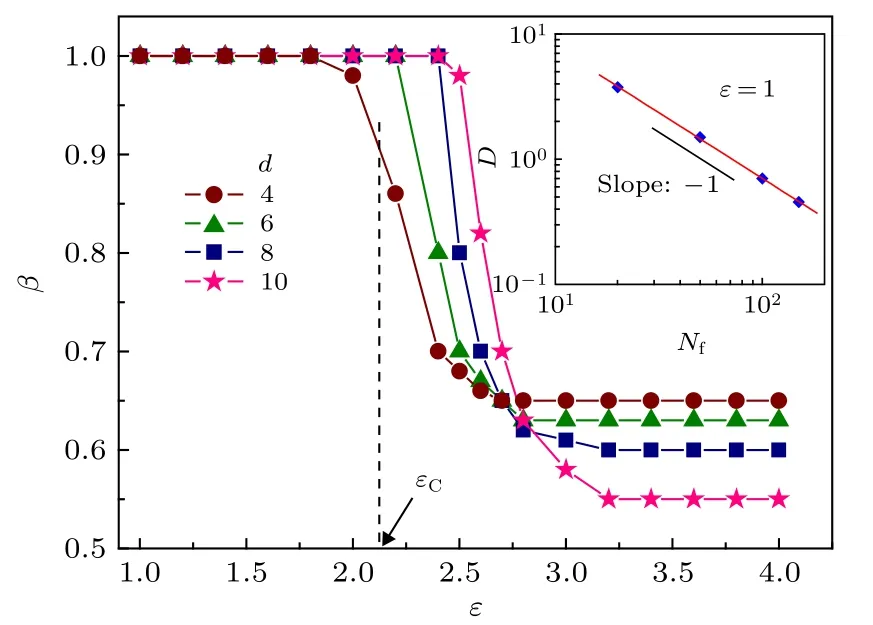
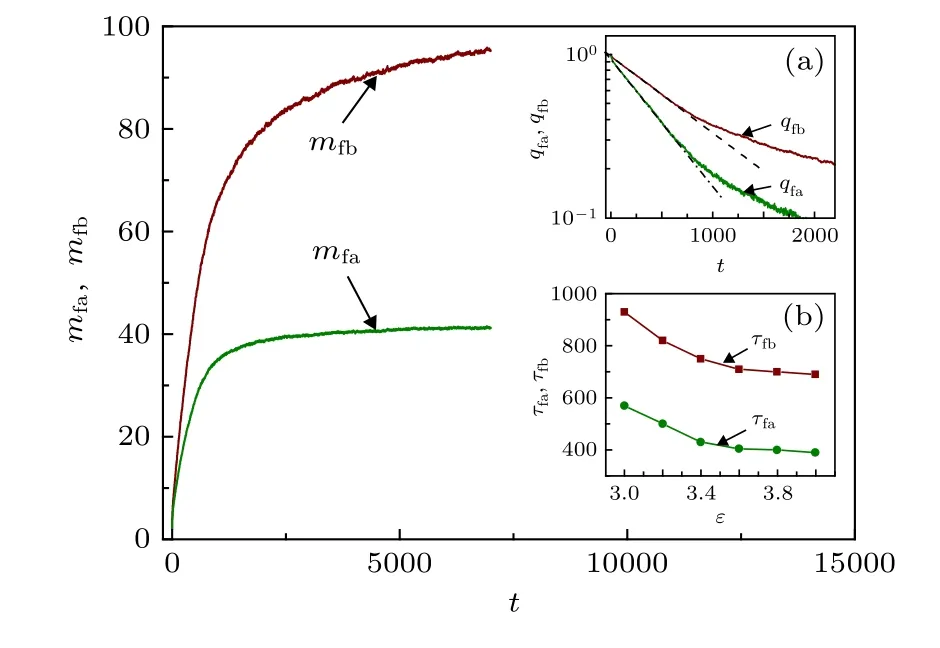
接下来, 研究了自由链的扩散. 图5 给出了自由链质心均方位移(Dr)2随时间t 的演化, 其中Nf= 50, Nb= 10, d = 10, 对应临界吸附能eC≈2.55. 结果表明, 在脱吸附态(e < eC), 自由链扩散快慢几乎与e 无关; 但在吸附态(e > eC), 随着e 增大, 自由链扩散进行得越来越慢. 特别地, 当e 比较大时, 自由链处于强吸附状态, 自由链节一旦与分子刷链节吸附就很难脱离, 因此在整个模拟时间内自由链只有微小移动, 如图5 所示. 另外发现, 对于任意给定的吸附能e, (Dr)2随时间t 的变化均存在简单的幂次关系 (∆r)2=2Dtβ. 当e 亚扩散是反常扩散(包括亚扩散(0 < b < 1)和超扩散(b > 1))的一种. 尽管反常扩散的机制可能有很多, 但Cherstvy 和Metzler[30]认为反常扩散主要存在于以下三种情形: 1)分形环境中的扩散; 2)黏弹环境中的扩散; 3)粒子在运动过程中存在一系列明显的吸附受限事件. 对于第三种情形, b 满足0 < b < 1, 即扩散为亚扩散. 在我们的模型中, 当e ≥ eC时, 自由链被分子刷吸附, 自由链上任意链节在运动过程中都会不断地与分子刷链节吸附(受限)和解吸附(脱离受限), 每次吸附到解吸附都需要经历一定的受限时间. 因此, 自由链的扩散属于反常扩散的第三种情形, 即亚扩散.此时, b 的取值与吸附点位的分布密度有关.Morrin 和Schwartz[31]曾研究了聚乙二醇(PEG)分子链在疏水三甲基硅烷(TMS)表面的扩散(其中TMS 对PEG 分子链有吸附作用), 发现目标PEG 分子链的扩散为亚扩散且标度指数b 与其他PEG 在TMS 表面的覆盖度有关. PEG 浓度越高,覆盖度越大, TMS 对目标PEG 分子链的吸附点位就越少. 实验结果表明,b随PEG 浓度(覆盖度)呈非单调变化. 在中等浓度(中等覆盖度)区域,b值在0.4—0.7 之间且随PEG 浓度(覆盖度)的增大而减小. 在我们的模型中, 分子刷链间距d反映分子刷的疏密程度, 即对自由链吸附点位的疏密程度.d越大, 吸附点位就越稀疏. 因此,指数b与d有关, 但没有一个普适值. 结果表明,当e≫eC时,b在0.6 附近且随d的增大而略有减小, 如图6 所示. 这与实验结果存在一定的相似性. 图5 吸引作用能e 不同时自由链质心均方位移(Dr)2 随时间t 的演化, 其中Nf = 50, Nb = 10, d = 10Fig. 5. The evolution of the mean square displacement of the center of mass of the free polymer (Dr)2 for different e,where Nf = 50, Nb = 10 and d = 10. 图6 d 取不同 值时, b 随e 的 变化, 其中Nf = 50, Nb =10. 插图: 弱吸附作用下(e = 1), 自由链扩散系数D 随链长度Nf 的变化Fig. 6. The dependence of b on e for different d, where Nf =50 and Nb = 10. The inset presents the dependence of the diffusion coefficient D on Nf at small e = 1. 最后研究了e>eC条件下自由链吸附的动态过程. 在吸附过程中, 自由链吸附链节数(mfa)会不断增大, 同时自由链-分子刷链节接触对数(mfb)也会不断增大. 图7 给出e= 3 时mfa和mfb随时间的演化, 其中Nf= 50,Nb= 10,d=10, 对应临界吸附能eC≈ 2.55. 由图7 可以看出,自由链的吸附是一个快速的过程,mfa和mfb均随时间t快速增大并分别趋于饱和值mfae和mfbe. 由于自由链的一个链节可以与多个分子刷链节接触,因此当吸附达到稳定时,mfbe总是大于mfae, 如图7所示. 图7 自由链吸附链节数mfa 和自由链-分子刷链节接触对 数mfb 随 时 间t 的 演 化, 其 中Nf = 50, Nb = 10, d = 10,e = 3. 插图: (a)弛豫函数qfa(t)和qfb(t)随时间的演化;(b)自由链吸附时间tfa 以及自由链-分子刷链节接触对数弛豫时间tfb 随吸引作用能e 的变化, 其中Nf = 50, Nb =10, d = 10Fig. 7. The evolution of the number of the adsorbed segment of the free polymer (mfa) and that of the number the segment of polymer brush contacting with the free polymer(mfb), where Nf = 50, Nb = 10, d = 10 and e = 3. The insets: (a) The evolution of the relaxation function qfa(t) and qfb(t); (b) the dependence of the adsorption time tfa of the free polymer and the relaxation time of the number of segment of brush contacting with the free polymer tfb on the adsorption energy e, where Nf = 50, Nb = 10 and d = 10. 为了确定自由链的吸附时间, 定义自由链吸附链节数弛豫函数qfa(t): qfa(t)随时间t呈指数衰减且可表示为[15] 其中tfa为自由链吸附时间(或自由链吸附链节数弛豫时间). 模拟结果表明, 在0.4 在0.4 图7 插图(b)给出了自由链吸附时间tfa以及自由链-分子刷链节接触对数弛豫时间tfb随吸附作用能e的变化. 由图可以看出, 随着吸附作用能e增大,tfa和tfb均单调减小, 这说明增大吸附作用能可以有效地加快自由链的吸附过程. 同时, 随着d减小或Nb增大, 自由链周围的分子刷链节增多, 自由链越容易吸附在分子刷上, 从而导致自由链的吸附过程加快(结果未给出). 另外, 我们发现在相同参数条件下tfb总是比tfa大, 这意味着自由链吸附在分子刷上后并没有马上达到稳定吸附,周围的分子刷链节仍不断地向其靠近并最终形成稳定吸附. 也就是说, 整个吸附过程包含了自由链的吸附和分子刷向自由链的扩散两种运动, 而且可分为两个阶段: 第一阶段, 自由链的吸附占主导,自由链在分子刷吸附作用下不断靠近并吸附于分子刷上; 第二阶段, 分子刷的扩散占主导, 分子刷链节逐渐向自由链靠近并形成稳定吸附. 用Monte Carlo 方法模拟研究了一条自由高分子链在分子刷上的吸附. 模拟结果表明, 随着自由链与分子刷之间吸附能e的增大, 自由链出现由脱吸附态到吸附态的转变. 临界吸附能eC几乎与自由链长度无关, 但随着分子刷链长Nb的减小或分子刷链间距d的增大而增大. 当e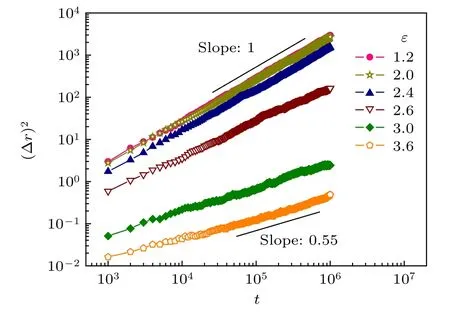
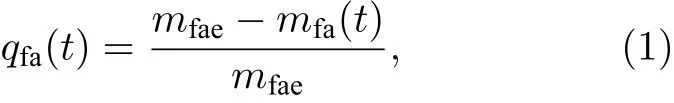
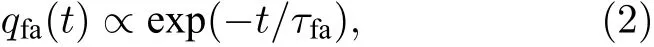
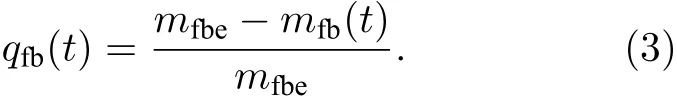
4 结 论
