借助几何直观让数学学习深度发生

浙江省余姚市泗门镇中心小学 胡高生

几何直观对于学生学习数学有着重要的意义。几何直观主要指的是通过图形去描述问题和分析问题，借助于几何将一些复杂的问题简单和明了化。几何直观能够帮助学生理解数学知识，让学生形成一种数学思维。作为小学数学教师，应该注重在课堂中对于几何直观的使用，培养学生几何直观的能力，进而全面地提高学生的数学素养。

一、借助几何直观，生动表现数学概念

在小学阶段的数学学习中，大家肯定会遇到一些数学概念，但是概念本身是比较抽象的，小学生的思维还停留在具象思维阶段，因此对于这些抽象的数学概念自然不能够更好地理解，这时候教师就可以采用几何直观来为学生提供更加直观和具象的内容。

例如在学习人教版小学数学三年级上册“分数的初步认识”时，教师可以给学生提供几个不同的图形，让学生通过折一折或者是涂一涂的形式表示这些图形的二分之一，然后讨论操作的结果，进一步总结出“二分之一”这一概念或者是属性。学生展示的图形有的是圆形，有的是三角形，但是为什么表示的部分都是二分之一呢？通过教师的引导，学生总结出无论是哪一种图形，因为把它平均分成了两份，那么其中的一份就是表示这个图形的二分之一。通过让学生结合具象的图形进行实际操作，学生逐渐地过渡到了分数的概念中，增强了利用具象图形来表示抽象的概念的能力，提高了学生对于数学的敏感程度。

二、利用几何直观，深层构建计算算理

运算教学在小学阶段非常重要，教师在教学中将更多的关注点放在了计算的结果或者是计算的方法上，但是忽视了计算原理，那么就会使得学生在完成练习时并不能够透彻地理解一道题目。这时候教师就需要努力将抽象的算法具象化，运用几何直观来实现这样的教学目标。

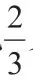
三、借助几何直观，提高学生解决问题能力

学生解决问题的能力也是数学素养中非常重要的一项内容。有些数学问题呈现出来过于烦琐，学生有的时候没有办法使用文字叙述来把握其中的关系，所以不能够把问题转化为自身的一种理解。教师就可以借助于几何直观的形式来启发学生解题的思路，让学生能够对问题进行一层层的分析和推理，通过这样的过程，学生能够充分地认识到几何图的意义，也能够找到分析问题的整体思路。

例如，在小学数学解决问题中会出现这样一个问题：某小学有一个长方形的花圃，长为8 米。在修建校园的时候，花圃长增加了3 米，那么花圃面积增加了18 平方米，原来花圃的面积是多少？这样的问题如果通过绘图形式呈现，往往能够给学生带来更加直观的信息，提高解题的效率。

四、借助几何直观，提高学生的想象力

几何直观不仅仅是让学生通过示意图来表示数量之间的关系，同时也希望学生能够借助图形有新的认识，利用图形进行推理。学生在利用几何直观进行比较和分析的过程中，有效地培养了创造性思维，同时让创造力得到了发展，也在某种程度上提高了推理能力和想象力。

例如，在学习人教版小学数学关于正方体、长方体的内容时，有一个问题是从平面图去判断几何体的方向。教师可以给学生展示长方体和正方体的模型，让学生从直观的角度观看不同角度下几何体的平面图，进而为学生这部分问题的解决打下基础。

小学阶段的数学知识存在着一定的抽象性和逻辑性，但是小学生的抽象思维还没有完全成熟，他们的认知还停留在具象思维阶段。为了能够帮助小学生更好地去理解这些抽象的知识，教师要充分利用几何直观来开展教学，培养学生在学习中利用几何直观解决问题的意识，让学生不断地积累这方面的经验，在提高学生运用几何直观能力的同时提高数学素养。