农村学校中考复习课上如何进行网格问题的教学——《网格问题初探》教学设计

■天津市咸水沽第四中学 刘志华

一、专题教学目标

1.了解网格的基本功能，学会借助网格作垂线、作平行线、等分线段等。2.会利用网格解决较基础的作图。

二、教学重难点

网格问题囊括很多方法，密切结合初中数学知识。在新课标对作图要求统领下，既考查了学生借助网格综合运用数学知识解决问题的能力，又提高了学生运用数学语言精准表述的能力。确定本课的教学重点是：学会利用网格作平行线、作垂线、等分线段等基本操作，并在此基础上进行中考题的思考和探究。教学难点是：知道作图的道理，让学生借助网格综合运用数学知识解决问题。

三、教学支持条件分析

借助信息技术工具，以几何画板为平台，更形象直观地体现平移、旋转等动态过程，绘制网格图。

四、教学过程设计（建议两课时）

（一）认识网格

1.网格具备什么？位置特征：平行线、垂线；数量特征：等长线段；图形特征：口、日、田，等等（特别强调：这些特征能赋予图形一些特殊关系，进而使图形的几何性质得以特殊化、数量化）。

2.我们能用网格做什么？(1)做平行（利用平移）；(2)做垂直（利用旋转）；(3)等分线段（利用A字型或X字型）；(4)做等角（利用三角函数）；(5)做部分长度为无理数的线段……师生活动：课前预留作业。教师提前录制微视频，把网格的位置特征、数量特征、图形特征形象化。

设计意图：学生快速进入网格情境，为后续学习做铺垫，明确网格的工具性特征，增加了神秘感，激发了学生学习兴趣。

（二）基本作图

1.如图1：(1)选格点A，B，C，过C点作线段AB的平行线；(2)选格点A，B，过B作线段AB的垂线；(3)选格点A，B，作线段AB的中垂线。

图1

2.如图2，（1）将线段AB平分，（2）在线段AB上有一点P，使AP∶BP=3∶4，画出点P。

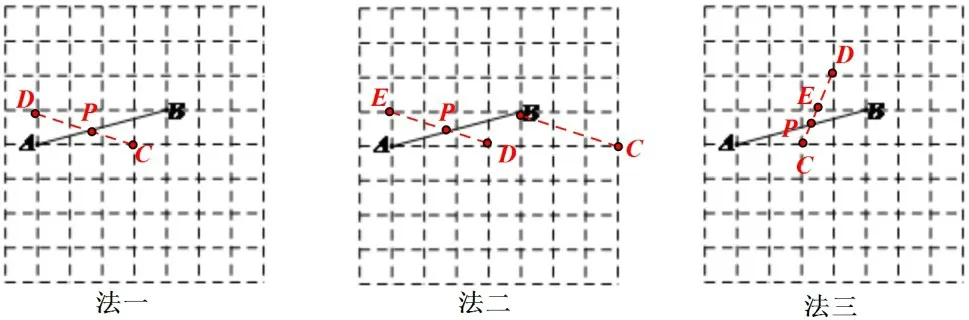
图2

法一：（构造X字型）取格点C，使AC=3，取格点D，使BD=4。连CD交AB于点P。

法二：（构造A字型）取格点C，使AC=7，取格点D，使AD=3，连接BC，过D作DE∥BC，交AB于点P。

法三：如果格不够，可以缩小比例，不要增加格点，如图构造X字型，相似比为1.5∶2。

师生活动：学生慢慢熟悉借助网格进行作图，并理解其中蕴含的数学道理。

设计意图：通过以上基本作图练习，让学生体会将全等、相似等数学知识运用到网格中的必要性，求解这类问题的关键，还是要抓住图形变换的要素，找准位置关系。

（三）案例分析

2017年天津市中考第（18）题：

如图3，在每个边长为1的小正方形网格中，点A，B，C均在格点上。

（Ⅰ）AB的长等于______；

（Ⅱ）在△ABC的内部有一点P，满足SΔPAB∶SΔPBC∶SΔPCA=1∶2∶3

请在以下网格中，用无刻度的尺，画出点P，并要说明点P的位置是如何找到的（不证明）

师生活动：学生进一步分析、体会。教师引导学生回忆数学知识(共边三角形的性质、图形面积割补法等)总结两种思路：

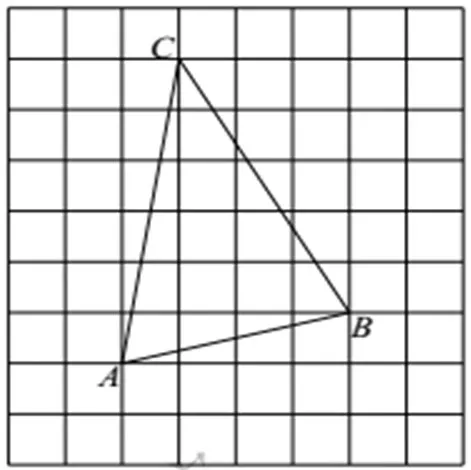
图3

思路1：运用共边三角形的性质。

如图4，假设所求点P已作出，那么它需要同时满 足 两 个 条 件：①SΔPAB∶SΔPBC=1∶2，②SΔPBC∶SΔPCA=2∶3，不妨先放弃条件②，如图5，延长BP交AC于点D，由具有相同底的两个三角形面积比等于对应高之比，结合相似三角形性质可得SΔPAB∶SΔPBC=AD∶CD=1∶2。只要在AC作出点D，使AD:CD=1∶2，则满足条件①的点P都在BD上；同理，如图6，在AB上取点E，当BE∶AE=2∶3时，满足条件②的点P都在CE上。综上，BD和CE的交点即为所求。

在这里利用平行线分线段成比例定理和相似三角形的性质把线段按指定的比值分割，如图7作出点D、E，连接AE和BD，如图8，交点P即为所求。

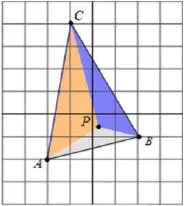
图4

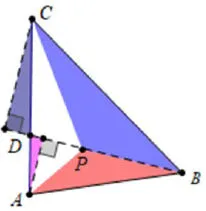
图5

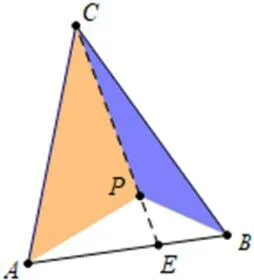
图6

图7

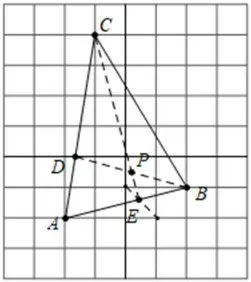
图8

思路2：等积变形

由SΔPAB∶SΔPBC∶SΔPCA=1∶2∶3，易 知，取AB中点E，如图9，则SΔEAC∶SΔABC=1∶2。过点E做EF//AC交BC于F，如图10，易知当点P在EF运动时，有。所以在△ABC内部，所求的点P一定在EF上；同理，如图11、12，分别作出AB和AC三等分点G，H，则所求点P一定在GH上。综上，如图13，EF和GH的交点即为所求。

图9

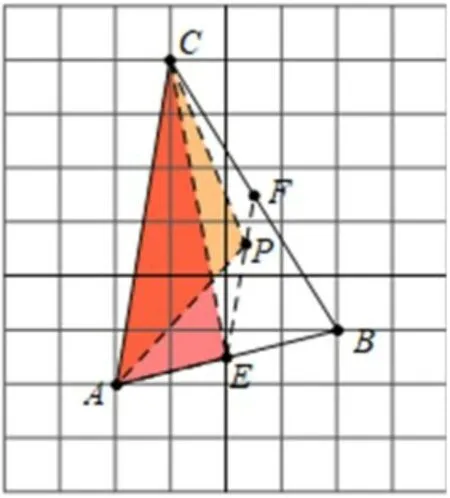
图10

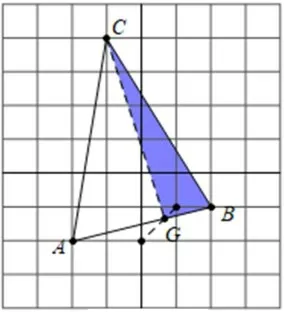
图11

图12

图13

思路1结合共边的两三角形高的比是两相似三角形的相似比，先找到符合使S△PAB∶S△PBC=1∶2和S△PBC∶S△PCA=2∶3所在的直线，两线相交即为所求。学生熟知三角形中线，能将三角形分成面积相等的两部分，以此延伸三角形面积3等分，甚至n等分的方法。思路2和思路1相似，区别在于运用同底等高的三角形面积相等的知识，得到三角形面积的二分之一、三分之一，再找到交点。设计意图：此题有利于提高学生借助网格综合运用数学知识解决问题的能力。题目以网格为载体，以学生熟悉的等分面积为问题，增强了解决问题的信心。

（四）学以致用

如图14，在每个小正方形的边长为1的网格中，点A、B、C均在格点上。

（1）AB=_____。（2）请你借助网格和无刻度的直尺，作出一个以AB为边的矩形，使矩形的面积等于△ABC的面积，并简要说明你的作图方法(不证明)。

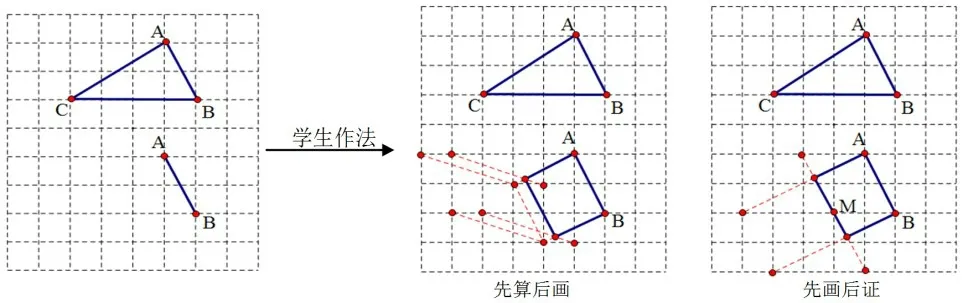
图14

师生活动：教师布置习题，根据课上的实际情况让学生选作。设计意图：巩固基本作法，引导学生联系相关数学知识，总结解题策略。可以先去掉网格背景，算出矩形边长，还原数学本质，研究通法（先算后画）；也可以利用网格特征，猜测或拼凑，然后再论证（先画后证）。

（五）课堂小结

1.这节课学到了哪些网格基本作图？2.网格问题的解题策略是什么？师生活动：从学习内容、基本方法、解题策略几个方面进行概括总结。设计意图：借助小结，引导学生复习基本作图、基本策略。

五、几点思考

（一）从学生实际出发，低起点缓步推进

网格作图问题立意新颖、综合性强，对于农村校的学生普遍感到困难。首先应引导学生从位置、数量、图形等方面领会网格自身的特征赋予了图形的特殊关系，进而使图形得以特殊化、数量化。接着以基本作图为载体，让学生体会网格可以作为作图工具替代传统刻度尺和圆规，这样增加了数学味道，更注重挖掘其蕴含的数学道理，激发学生的探究兴趣。

（二）从中考真题入手，落实综合实践课程内容

新课标指出：综合与实践的内容，设置的目的在于培养学生的问题意识、应用意识，积累活动经验，提高解决问题的能力。师生一起探究中考题这道综合实践类问题，让学生运用教材原题提炼基本图形，再解决问题。这样预测结果，利用基本图形分析问题，有助于探索解决问题的思路，提升学生数学抽象、逻辑推理、直观想象、数据分析等数学素养。

（三）从总结通法着力，期待能抛砖引玉

笔者精选和例题有联系两道题，鼓励学生多角度探究，在实践的过程中注意引导学生明确作图的道理，把握几何图形的特征和性质，找到各元素之间的关系，抓住本质、总结通法，从而巩固基础知识、基本技能，形成网格问题的基本活动经验，提升发现和提出问题、分析和解决问题的能力。

（四）从网格功能审视，今后要继续完善

考虑本节内容较难，笔者将本课设为两课时，尽管如此，还是有很多遗憾。比如进行了作平行线、作垂直、等分线段这三个基本作图的教学，对于其他基本作图还没有涉及，在以后的教学工作中，笔者会继续完善，继续研究，期待网格问题被更多的师生悦纳，让这么富有魅力的小小网格发挥最大的育人功效！